Как стать автором
Поиск
Написать публикацию
Обновить

Анализ распределения временных интервалов между покупками на R

Время на прочтение10 мин
Количество просмотров4.3K
R*Визуализация данных*Статистика в IT
Из песочницы

Известно, что интервалы между сообщениями в онлайн-чате подчиняются степенному распределению, как утверждали ученые из Цюриха и Вены в 2012 году, а интервалы между двумя последовательными покупателями или двумя последовательными звонками в колл-центре подчиняются экспоненциальному распределению, как утверждает википедия.

А вот автор статьи на Хабре про типичные распределения вероятностей сказал бы, что глупо постулировать принадлежность чего-то определенному распределению, потому что разные сущности могут вести себя по-разному при соответствующих допущениях. Экспоненциальное распределение, например, лишь частный случай более общего распределения Вейбулла, которое позволяет моделировать увеличивающуюся (или уменьшающуюся) со временем интенсивность событий (поступления звонков или прихода покупателей). Таким образом, экспоненциальное распределение покупателей в магазине - абстракция, которая лишь в общих чертах описывает реальность. Посмотрите, например, историю с автобусами на Хабре.

Вернемся к примеру с распределением интервалов между сообщениями в онлайн-чате. Результаты указанной статьи лучше посмотреть в интерпретации журнала Physics Today. Можно утверждать, что процесс отправки сообщений коренным образом отличается от процессов поступления звонков в колл-центр или прихода автобусов на остановку. Поэтому и распределения у них отличаются.

Я решил сделать ресёрч интервалов между собственными банковскими тратами за последние полгода и с помощью статистических методов на R определить, какому распределению эти интервалы будут подчиняться. Ожидается, что процесс совершения оплаты в большей степени должен быть похож на процесс отправки сообщений, чем на процесс поступления звонков или прихода покупателей, хотя бы потому, что исходит от первого лица.

Рисунок 1: Иллюстрация совершения банковских транзакций, формирования временных интервалов между ними и формулировка задачи.
Рисунок 1: Иллюстрация совершения банковских транзакций, формирования временных интервалов между ними и формулировка задачи.

В статье я представляю:

  1. Код на R для анализа любых временных интервалов.

  2. Подбор экспоненциального и степенного распределения под данные с помощью метода максимального правдоподобия (MLE). Для экспоненциального я использую fitdistr() из пакета MASS, а для степенного fit_power_law() из пакета igraph.

  3. Проверку данных на соответствие подобранному распределению с помощью теста Колмогорова-Смирнова. Я использую функцию ks.test() из пакета stats.

В конце статьи я оставляю ряд открытых вопросов и буду рад, если в комментарии придет эксперт по подбору распределений под данные и сможет их прояснить.

Выгрузка данных

Для начала стоит выгрузить данные из банковского приложения. Как это сделать в Тинькоф или Рокетбанк, можно подсмотреть в статье на Хабре про статистику расходов по МСС.

В статье я буду рассматривать только интервалы размером менее суток, потому что для анализа интервалов продолжительностью более суток моих данных маловато (я не слишком часто оказывался вдали от цивилизации или сидел в спецприемниках).

Раскройте для просмотра кода на R
library(data.table) # для работы с дата-фреймами

operations <- fread('operations.csv')

operations <- operations[`Сумма операции` < 0]  # Оставим только покупки
operations <- operations[`Статус` == 'OK']      # Оставим только успешные покупки
operations <- operations[`Описание` != 'Комиссия за операцию']   
                                                # Уберем комиссию за переводы
operations <- operations[`Номер карты` != '']   # Уберем плату за обслуживание карты

# 1. Переводим строку в числовой формат с помощью strptime()
operations[, time := strptime(`Дата операции`, "%d.%m.%Y %H:%M:%S")]

# 2. Добавим в датафрейм разность между временем двух последовательных покупок (в секундах)
operations <- cbind(operations, as.numeric(diff(operations$time)))
colnames(operations)[17] <- "intervals" #Переименуем колонку для красоты

# 3. Переведем интервалы в часы и сделаем интервалы положительными
operations$intervals <- operations$intervals / (60*60)*(-1)
nrow(operations[intervals > 24])

# 4. Оставим только успешно проведенные операции
# интервалы меньше 24 часов и строго больше нуля
operations <- operations[intervals < 24, ,]
nrow(operations[intervals > 8 & intervals < 24])

UPD: Прошу обратить внимание, что при очистке я не удалял регулярные платежи. Их очень мало в моей выборке, но на них стоит обратить внимание в случае большого количества подписок.

Итоговый вектор с интервалами, использованный для написания статьи, я выложил в открытый доступ.

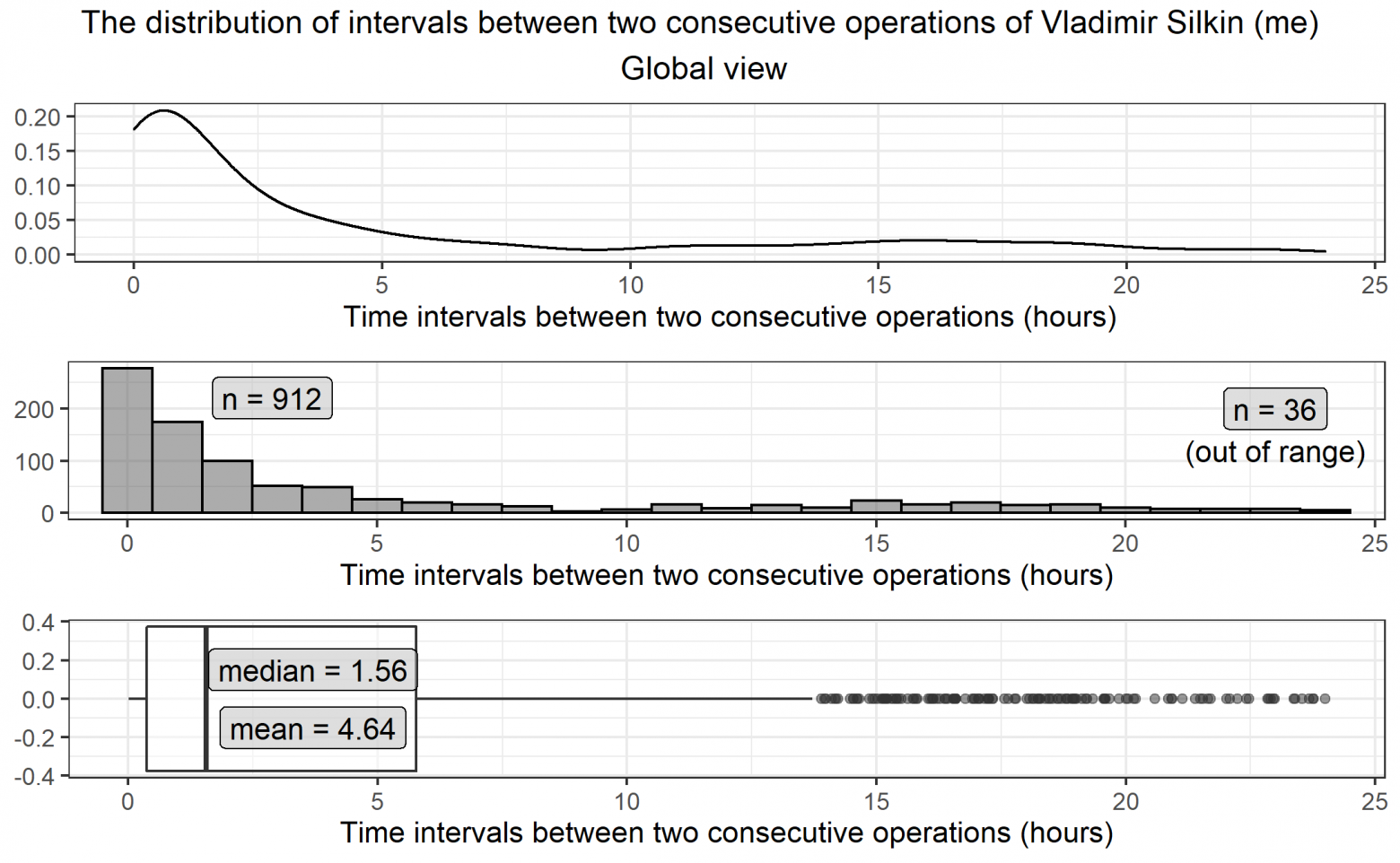
Смотрим на данные глобально

После выгрузки и очистки посчитаем основные описательные статистики среди интервалов до 24 часов. Таких оказалось 912, а 36 интервалов в рассматриваемый промежуток не попали.

  • Медиана (ч): 1.56

  • Среднее (ч): 4.64

Построим базовые графики - плотность, гистограмму и боксплот.

Раскройте для просмотра кода на R
# Добавим в данные качественную переменную, разделяющую наши данные на 2 распределения
operations$distr <- ifelse(operations$intervals < 8, 'exp', 'norm')

# Медиана и среднее для экспоненциального распределения
med_exp <- median(operations[intervals < 8, intervals,])
mean_exp <- mean(operations[intervals < 8, intervals,])

# Медиана, среднее и стандартное отклонение для нормального распределения
med_norm <- median(operations[intervals > 8, intervals,])
mean_norm <- mean(operations[intervals > 8, intervals,])
sd_norm <- sd(operations[intervals > 8, intervals,])

# Гистограмма с цветовым разделением данных.
g1 <- ggplot(data = operations, aes(x = intervals, fill = distr)) + 
  geom_histogram(alpha = 0.5, binwidth = 1, show.legend = FALSE, colour = "black") + 
  coord_cartesian(xlim = c(0, 24)) +
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  annotate("label", x = 4, y = 150, 
           size = 4, 
           label= "n = 722",
           fill="red", alpha = 0.25) + 
  annotate("label", x = 16, y = 100, 
           size = 4, 
           label= "n = 190", 
           fill="#00AFBB", alpha = 0.25) + 
  theme_bw() 

# Двойной боксплот так же с разделением.
g2 <- ggplot(data = operations, aes(x = intervals, fill = distr)) + 
  geom_boxplot(alpha = 0.5, show.legend = FALSE)+ 
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  
	# Медиана и среднее длинных интервалов
  annotate("label", x = 16, y = -0.07, 
           size = 4, 
           label= paste("median =", round(med_norm, 2)) ,
           fill="#00AFBB", alpha = 0.25) + 
  annotate("label", x = 16, y = -0.195, 
           size = 4, 
           label = paste("mean =", round(mean_norm, 2)), 
           fill = "#00AFBB", alpha = 0.25) + 
  annotate("label", x = 16, y = -0.318, 
           size = 4, 
           label = paste("sd =", round(sd_norm, 2)), 
           fill = "#00AFBB", alpha = 0.25) + 

  # Медиана и среднее коротких интервалов
  annotate("label", x = 2, y = 0.27, 
           size = 4, 
           label = paste("median =", round(med_exp, 2)),
           fill="red", alpha = 0.2) + 
  annotate("label", x = 2, y = 0.13, 
           size = 4, 
           label = paste("mean =", round(mean_exp, 2)), 
           fill = "red", alpha = 0.2) + 

  coord_cartesian(xlim = c(0, 24)) +
  theme_bw() 

# Соединяем графики вместе
grid.arrange(g1, g2, nrow = 2, top = "The distribution of intervals between two consecutive operations of Vladimir Silkin (me)\n Focus on two parts of distribution")
Рисунок 2: Распределение временных интервалов между двумя последовательными покупками, визуализированное тремя способами — плотностью, гистограммой и boxplot.
Рисунок 2: Распределение временных интервалов между двумя последовательными покупками, визуализированное тремя способами — плотностью, гистограммой и boxplot.

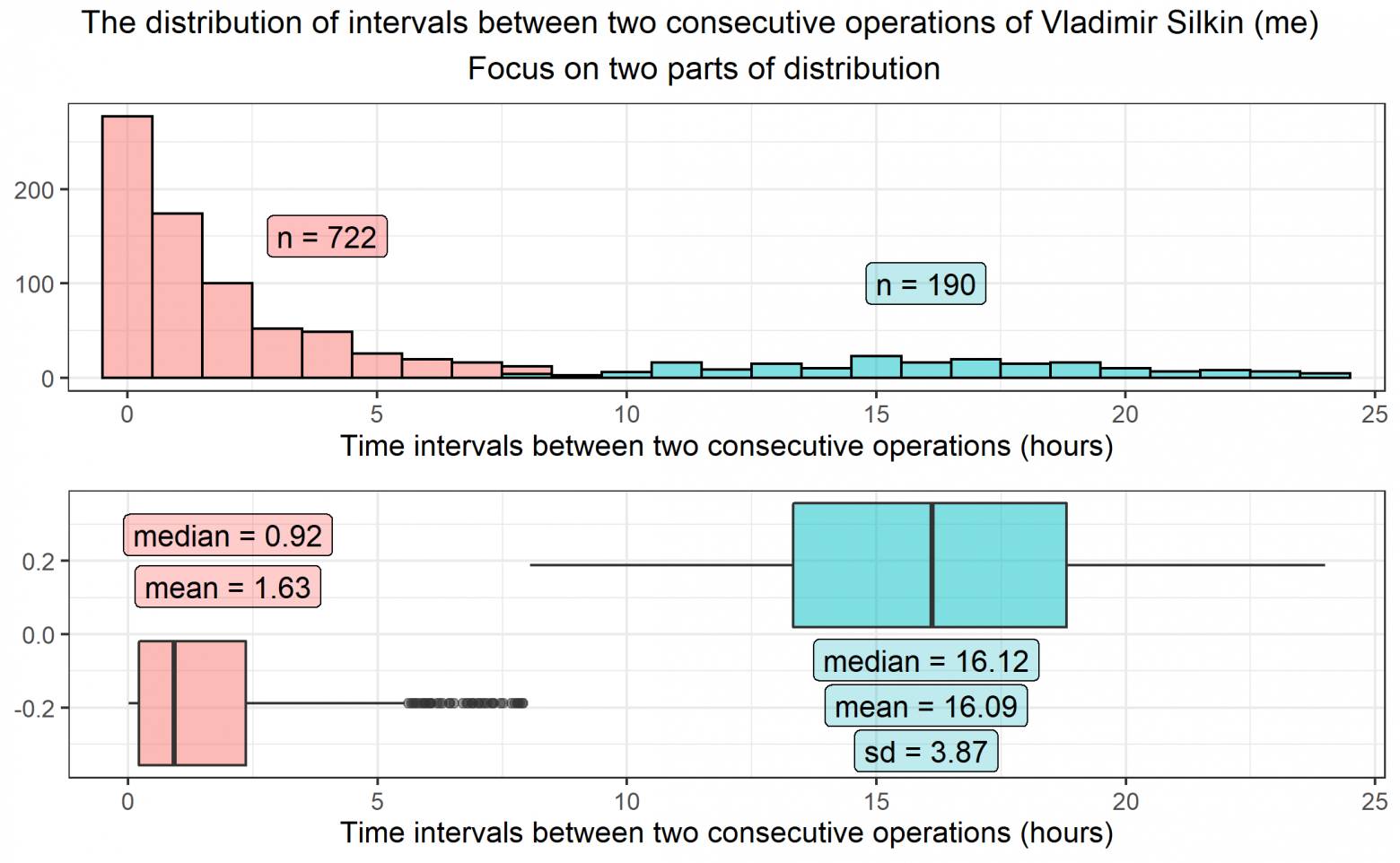
После анализа полученного распределения я принимаю решение разделить данные на 2 группы -- примерно от 0 до 8 часов и от 8 до 24.

  • Распределение первых похоже на экспоненциальное или степенное, состоит из небольших промежутков и может быть связано с тратами, проходящими по определенным паттернам (сходить на прогулку и в разных местах много чего купить). Это мое оценочное суждение.

  • Распределение вторых похоже на нормальное. Оно состоит из промежутков около среднего времени бодрствования - 16 часов.

Можно ли описать данные указанными распределениями, узнаем чуть позже. Давайте сперва взглянем на них более детально.

Берем фокус на двух частях распределения

Экспоненциальное/степенное, которое связано небольшими промежутками трат обозначено на следующем графике красным цветом. Околонормальное распределение данных возле среднего промежутка бодрствования обозначено синим цветом.

Раскройте для просмотра кода на R
# Добавим в данные качественную переменную, разделяющую наши данные на 2 распределения
operations$distr <- ifelse(operations$intervals < 8, 'exp', 'norm')

# Медиана и среднее для экспоненциального распределения
med_exp <- median(operations[intervals < 8, intervals,])
mean_exp <- mean(operations[intervals < 8, intervals,])

# Медиана, среднее и стандартное отклонение для нормального распределения
med_norm <- median(operations[intervals > 8, intervals,])
mean_norm <- mean(operations[intervals > 8, intervals,])
sd_norm <- sd(operations[intervals > 8, intervals,])

# Гистограмма с цветовым разделением данных.
g1 <- ggplot(data = operations, aes(x = intervals, fill = distr)) + 
  geom_histogram(alpha = 0.5, binwidth = 1, show.legend = FALSE, colour = "black") + 
  coord_cartesian(xlim = c(0, 24)) +
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  annotate("label", x = 4, y = 150, 
           size = 4, 
           label= "n = 722",
           fill="red", alpha = 0.25) + 
  annotate("label", x = 16, y = 100, 
           size = 4, 
           label= "n = 190", 
           fill="#00AFBB", alpha = 0.25) + 
  theme_bw() 

# Двойной боксплот так же с разделением.
g2 <- ggplot(data = operations, aes(x = intervals, fill = distr)) + 
  geom_boxplot(alpha = 0.5, show.legend = FALSE)+ 
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  
  annotate("label", x = 16, y = -0.07, 
           size = 4, 
           label= paste("median =", round(med_norm, 2)) ,
           fill="#00AFBB", alpha = 0.25) + 
  annotate("label", x = 16, y = -0.195, 
           size = 4, 
           label = paste("mean =", round(mean_norm, 2)), 
           fill = "#00AFBB", alpha = 0.25) + 
  annotate("label", x = 16, y = -0.318, 
           size = 4, 
           label = paste("sd =", round(sd_norm, 2)), 
           fill = "#00AFBB", alpha = 0.25) + 
    
  annotate("label", x = 2, y = 0.27, 
           size = 4, 
           label = paste("median =", round(med_exp, 2)),
           fill="red", alpha = 0.2) + 
  annotate("label", x = 2, y = 0.13, 
           size = 4, 
           label = paste("mean =", round(mean_exp, 2)), 
           fill = "red", alpha = 0.2) + 
  

  
  coord_cartesian(xlim = c(0, 24)) +
  theme_bw() 

# Соединяем график вместе
grid.arrange(g1, g2, nrow = 2, top = "The distribution of intervals between two consecutive operations of Vladimir Silkin (me)\n Focus on two parts of distribution")
Рисунок 3: Распределение временных интервалов между двумя последовательными покупками в зависимости от группы, в которую попал интервал — от 0 до 8 часов и от 8 до 24 часов.
Рисунок 3: Распределение временных интервалов между двумя последовательными покупками в зависимости от группы, в которую попал интервал — от 0 до 8 часов и от 8 до 24 часов.

1. Проверка на нормальность

Сперва разберемся с околонормальным распределением. Посчитаем вероятность получить такие как у нас и более выраженные отклонения от нормальности с помощью теста Шапиро-Уилка.

shapiro.test(operations[intervals > 8, intervals])

Получаем p.value \approx 0.03То есть, если наша выборка, действительно, взята из нормального распределения, то вероятность получить такие и сколько угодно более выраженные отклонения от нормальности случайно равняется 3%.

Раскройте для просмотра кода на R
g1 <- ggplot(data = operations[intervals > 8], aes(x = intervals)) + 
  geom_density(size = 1, 
               aes(color = 'real density function')) +
  stat_function(fun = dnorm, 
                aes(color = 'ideal normal distrubution'),
              args = list(16,4), 
              size = 1) +
  scale_colour_manual(NULL, values = c("darkgreen", "black")) +
  
  geom_histogram(aes(y = stat(count) / sum(count)), 
                 fill = "#00AFBB",
                 alpha = 0.4, 
                 colour = "black",
                 binwidth = 1) + 
  coord_cartesian(xlim = c(8, 24)) +
  
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  theme_bw() +
  theme(legend.position = c(0.82, 0.85), 
        legend.background = element_rect(fill = "white", color = "black")) 

# Я использую функцию для соединения графиков для более красивого отображения
grid.arrange(g1, nrow = 1, top = "The distribution of intervals between two consecutive operations of Vladimir Silkin (me) \n Long intervals (longer than 8 hours and shorter than 24 hours)")
Рисунок 4: Гистограмма распределения временных интервалов между двумя последовательными покупками для группы интервалов от 8 до 24 часов, оригинальная функция плотности вероятности (черная кривая) и функция плотности для идеально нормального распределения (пунктирная кривая).
Рисунок 4: Гистограмма распределения временных интервалов между двумя последовательными покупками для группы интервалов от 8 до 24 часов, оригинальная функция плотности вероятности (черная кривая) и функция плотности для идеально нормального распределения (пунктирная кривая).

На данном этапе я не стану пользоваться общепринятым порогом значимости в 5% и отклонять нулевую гипотезу о том, что выборка взята из нормального распределения. Подчеркну здесь, что выборка интервалов в промежутке от 12 до 20 часов имеет предпосылки к нормальности и гипотеза об их нормальном распределении требует дальнейшего анализа и проверки.

2. Подбор экспоненциального и степенного распределений.

Теперь попробуем фитануть плотность вероятности с помощью двух распределений - экспоненциального и степенного. Они перед вами.

\begin{gather} f_{exp}(x) = \alpha \, e^{-\alpha \, x} \\ f_{pow}(x) = (\alpha-1)\, x_{min}^{\alpha-1}\, x^{-\alpha} \end{gather}

Множитель перед степенной функцией во втором уравнении возникает из-за необходимости нормировки распределения, а сам степенной закон подбирается к данным, начиная от указанного x_{min}. В качестве него я буду брать минимальное значение временных интервалов — 0.004 часа или 14 секунд.

В работе Data-Scientist`а нет ничего сложного. Главное — подгрузить нужные библиотеки. (Маэстро)

library(MASS) # Для подбора экспоненциального распределения с помощью fitdistr()
library(igraph) # Для подбора степенного распределения с помощью fit_power_law()
library(stats) # Для проведения теста Колмогорова-Смирнова

Фитуем данные экспоненциальным распределением:

fit_e <- fitdistr(operations[intervals < 8, intervals], "exponential")
fit_e$estimate[1][[1]] # alpha
fit_e$sd[1][[1]] # alpha_error
ks.test(operations[intervals < 8, intervals], "pexp", fit_e$estimate, exact = TRUE)$p.value #p.value

Получим \alpha \approx 0.61и p.value \sim 10^{-10}

Первое найдено с помощью метода максимального правдоподобия, а второе - с помощью теста Колмогорова-Смирнова.

Физический смысл результатов теста такой же, как и у результатов теста Шапиро-Уилка: если в генеральной совокупности данные, действительно, распределены экспоненциально, то вероятность получить такие и сколь угодно выраженные отклонения от экспоненциального распределения случайно, практически равна нулю. Про рассчитываемую в тесте статистику можно почитать в англоязычной статье википедии.

Фитуем данные степенным распределением:

fit_p <- fit_power_law(operations[intervals < 8, intervals], 
                       xmin = min(operations$intervals), 
                       implementation = "plfit")
# В xmin передается точка, начиная с которой выполняется подбор распределения

fit_p$alpha # alpha
fit_p$KS.p  # p-уровень значимости из теста Колмогорова-Смирнова

Получим \alpha \approx 2.05и p.value \approx 10^{-7}

В случае со степенным распределением p.value повышается, но все равно не достигает ни одного общепринятого порога значимости.

Составим итоговую таблицу с результатами:

Equation

Parameter

Significance

f_{exp}(x) = \alpha \, e^{-\alpha \, x}

\alpha \approx 0.61

p.value \sim 10^{-10}

f_{pow}(x)=(\alpha-1)\,x_{min}^{\alpha-1}\,x^{-\alpha}

\alpha \approx 2.05 \:\:\: x_{min} \approx 0.004

p.value \sim 10^{-7}

Посмотрим, как будут выглядеть наши фиты на графике.

Раскройте для просмотра кода на R
# Напишем, функцию, которая воспроизводит степенной закон
# Поместим в нее alpha и xmin, подобранные выше
plaw <- function(x){(fit_p$alpha-1)*0.004166667^(fit_p$alpha-1)*x^(-fit_p$alpha)}

gf <- ggplot(data = operations[intervals < 8], aes(x = intervals)) + 
  geom_density(size = 1) + 
  geom_histogram(alpha = 0.3,
                 aes(y = stat(count) / sum(count)),
                 binwidth = 1,
                 fill = "red",
                 colour = "black")+
  
  stat_function(fun = dexp, args = list(0.6136122), size = 1, colour = 'blue') +
  stat_function(fun = plaw, size = 1, colour = 'red') +

  coord_cartesian(xlim = c(0, 8), ylim = c(0, 0.5))+
  labs(x = "Time intervals between two consecutive operations (hours)", y = NULL) +
  theme_bw()
   
grid.arrange(gf, nrow = 1, top = "The distribution of time between two consecutive operations of Vladimir Silkin (me) \n 
Short intervals (shorter than 8 hours)")
Рисунок 5: Гистограмма распределения временных интервалов между двумя последовательными покупками для группы интервалов от 0 до 8 часов, оригинальная функция плотности вероятности (черная кривая), а также подобранные функции плотности — экспоненциальная (синяя) и степенная (красная).
Рисунок 5: Гистограмма распределения временных интервалов между двумя последовательными покупками для группы интервалов от 0 до 8 часов, оригинальная функция плотности вероятности (черная кривая), а также подобранные функции плотности — экспоненциальная (синяя) и степенная (красная).

UPD: Итоговым решением будет смесь распределения на Рис. 4 и распределения на Рис. 5. Первое будет входить с коэффициентом 3/4, потому что примерно 3/4 всех интервалов лежит в промежутке от 0 до 8 часов (см. Рис. 3). Второе распределение будет входить в смесь двух распределений с коэффициентом 1/4, потому что примерно 1/4 всех наблюдений лежит в промежутке от 8 до 24 часов.

\boxed{f_{density}(x) \approx \frac{3}{4}Exp(0.6) + \frac{1}{4} Norm(16, 4)}

Где Exp(0.6)— экспоненциальное распределение с параметром 0.6. Вместо него можно использовать степенное с параметром 2 (см. таблицу выше). А Norm(16, 4)— нормальное распределение со средним 16 и стандартным отклонением 4.

Выводы

Судя по финальной таблице с результатами, я не могу утверждать, что наши данные взяты из определенного распределения.

Я буду рад, если моя статья оказалось кому-то полезной. Если копать глубже, дальше и больше, то хотелось бы найти ответы на следующие вопросы:

  1. Есть ли какой-то физический смысл у медианы распределения интервалов? Сейчас мне кажется, что она характеризует способность человека принимать спонтанные решения о покупках, поэтому я ожидаю, что она будет увеличиваться с возрастом.

  2. Можно ли что-то сказать о теоретическом распределении интервалов между транзакциями и можно ли на основе полученных результатов утверждать о принадлежности к нему наших данных?

Теги:
Хабы:
Всего голосов 10: ↑9 и ↓1+12
Комментарии11
16
Карма
0
Рейтинг
Владимир Силкин @volodya_research

Data Science

Отправить сообщение
СайтTelegram

Публикации

Истории

Работа

Data Scientist
62 вакансии

Ближайшие события

16 января
Вебинар «Практикум Cloud.ru Evolution: знакомство с облаком»
Онлайн
Больше событий в календаре
Разработка
25 – 26 апреля
IT-конференция Merge Tatarstan 2025
Казань
Больше событий в календаре
Разработка
Маркетинг
Другое

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2024, Habr