AC130 11 сен 2021 в 16:33

Вероятность счёта серии матчей в бернуллиевской модели

5 мин

2.4K

Недавно, при просмотре неофициального онлайн-турнира по одной соревновательной игре, я ознакомился со следующим утверждением: для двух команд, равных по силе, т.е. когда исход матча моделируется броском симметричной бернуллиевской монетки, при игре в формате "до двух побед" вероятность счёта "в одни ворота", т.е. 2-0/0-2, равна вероятности счёта не "в одни ворота", т.е. 2-1/1-2. Это утверждение заставило меня вытащить из глубин памяти знания школьной комбинаторики и теорвера. Приведу небольшие заметки по данному вопросу.

Сценарий

Две команды — команда 0 и команда 1 — играют серию матчей. Результаты разных матчей серии являются независимыми случайными величинами со следующим распределением. Вероятность победы команды 0 в матче есть , вероятность победы команды 1 есть . Считаем что p+q=1 , т.е. ничьей быть не может.

Серия матчей играется в формате "first to ", т.е. до тех пор, пока некая команда не одержит N > 0 побед в серии матчей. Формат "first to " (FT ) эквивалентен формату "best of 2N-1 " (BO 2N-1 ), где победитель определяется на основании серии матчей длины 2N-1 — если некая команда уже одержала побед, то её оппонент не может одержать более N-1 победы, т.е. не может выиграть.

Завершившуюся серию матчей можно представить в виде последовательности нулей и единиц, где на позиции означает, что матч под номером выиграла команда 0, а на позиции означает, что матч выиграла команда 1. Пример такой последовательности:

$0 \, 0 \, 1 \, 0 \, 1 \, 0$

В данном примере команда 0 выиграла со счётом 4-2 в FT4/BO7. В дальнейшем для обозначения счёта будем также использовать запись следующего вида: (x_0, x_1) , где x_0 есть число побед команды 0, а x_1 есть число побед команды 1. Т.е. счёт выше можно записать в виде (4, 2) . Любой счёт завершившейся серии матчей может быть представлен в виде (N, x) в случае победы команды 0, и (x, N) в случае победы команды 1, где $0 \le x < N$ . Заметим также что команда, победившая в серии матчей, обязана победить в последней игре серии, т.е. в случае победы команды 0 последовательность должна заканчиваться на , в случае победы команды 1 — на . Число нулей в последовательности есть число побед команды 0, число единиц в последовательности есть число побед команды 1.

Вероятность определённого счёта в серии матчей

Серия матчей между двумя командами, где в каждом матче результат (победа команды 0 или команды 1) является случайной величиной с указанными выше вероятностями, может быть моделирована как последовательность случайных величин, подчиняющихся распределению Бернулли. Если результаты отдельных матчей независимы, то вероятность выпадения последовательности есть произведение вероятностей отдельных элементов. К примеру, для рассмотренной выше последовательности $0 \, 0 \, 1 \, 0 \, 1 \, 0$ вероятность именно такой серии матчей есть $p \cdot p \cdot q \cdot p \cdot q \cdot p =p^4 q^2$ . Однако, одному и тому же счёту могут соответствовать разные серии матчей. К примеру, счёт (4, 2) может получиться из следующих серий:

$1 \, 1 \, 0 \, 0 \, 0 \, 0, 1 \, 0 \, 1 \, 0 \, 0 \, 0, 1 \, 0 \, 0 \, 1 \, 0 \, 0, 1 \, 0 \, 0 \, 0 \, 1 \, 0, 0 \, 1 \, 1 \, 0 \, 0 \, 0,$ $0 \, 1 \, 0 \, 1 \, 0 \, 0, 0 \, 1 \, 0 \, 0 \, 1 \, 0, 0 \, 0 \, 1 \, 1 \, 0 \, 0, 0 \, 0 \, 1 \, 0 \, 1 \, 0, 0 \, 0 \, 0 \, 1 \, 1 \, 0.$

Необходимо подсчитать общее число возможных серий для произвольного счёта.

В серии матчей для счёта вида (N, x) (т.е. с победой команды 0) будет содержаться ровно нулей. Расставим единиц в последовательность из нулей. Для первой единицы есть ровно мест, в которые единицу можно поставить (так как последовательность должна заканчиваться нулём, а серия матчей — победой команды 0). Следующую единицу вставляем в последовательность из N+1 элементов, т.е. возможных мест для её постановки будет N+1 . Считая, что все вставляемые единицы уникальны, получаем

$N \cdot (N+1) \cdot (N+2) \cdot \dots \cdot (N+x-1)=\frac{(N+x-1)!}{(N-1)!}$

вариантов для вставки единиц в оригинальную последовательность из нулей. Вспомним теперь, что любая перестановка единиц не меняет получившуюся последовательность. Это значит, что результат необходимо поделить на число перестановок единиц, равное . Итого получаем:

$\frac{(N+x-1)!}{x! (N-1)!}=\binom{N+x-1}{x}=\binom{N+x-1}{N-1}.$

Итоговая вероятность счёта (N, x) есть $\binom{N+x-1}{N-1} p^N q^x$ .

Для счёта (x, N) , аналогичным образом, вероятность есть $\binom{N+x-1}{N-1} p^x q^N$ .

Проверку условия нормировки

$\sum_{x=0}^{N-1} \left[\binom{N+x-1}{N-1} p^N q^x + \binom{N+x-1}{N-1} p^x q^N \right] = 1$

оставим читателю.

Результаты

Первым делом посмотрим просто на распределение с произвольно выбранными параметрами:

График получился асимметричным в силу того, что $p \neq q$ , максимум вероятности достигается для счёта 3-10, что вполне соответствует заданным вероятностям. Как кривые меняются при изменении вероятностей победы в матче?

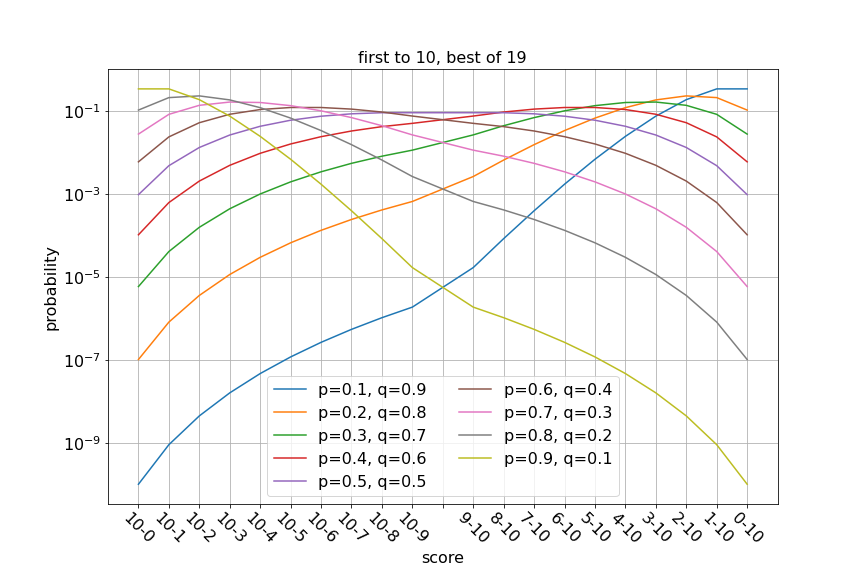
Кажется, что вероятность некоторых счётов одинакова — к примеру, при p=0.1, q=0.9 вероятность для 0-10 и 1-10 не поменялась. Обратимся к выведенным ранее формулам. Вероятность счёта (0, N) есть q^N . Вероятность счёта (1, N) есть N p q^N . Т.е. вероятности оказываются одинаковыми при $Np=1 \Leftrightarrow p=\frac{1}{N}$ . Несмотря на то, что вероятность более длинной серии матчей для счёта (1, N) меньше вероятности короткой серии матчей для счёта (0, N) , за счёт увеличения числа серий матчей, при которых достигается счёт (1, N) вероятность счёта (1, N) равна вероятности счёта (0, N) .

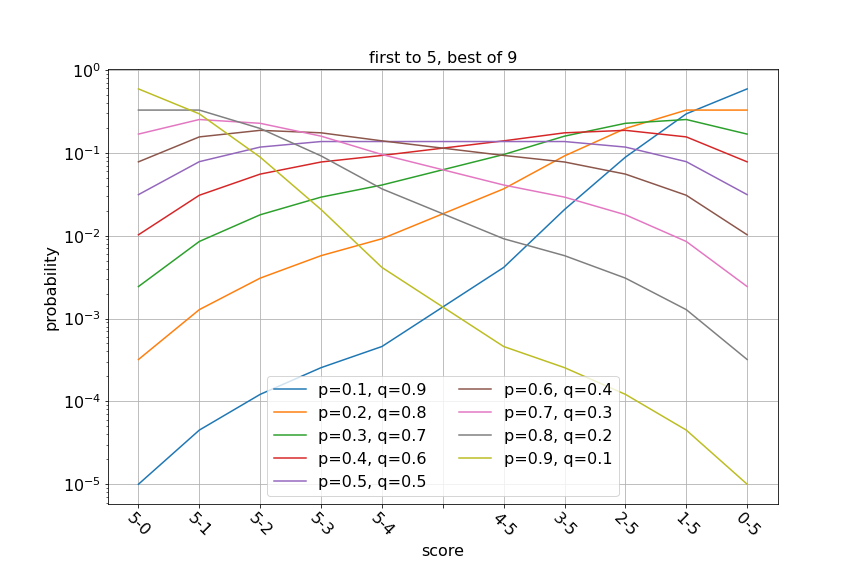
Для N=5 подобный эффект наблюдается уже при p=0.2, q=0.8 и p=0.8, q=0.2 соответственно, тогда как для p=0.1, q=0.9 и p=0.9, q=0.1 вероятность есть монотонная функция от счёта. Рассмотрение утверждения о том, что вероятность является монотонной функцией от счёта для любых случаев, когда $p<\frac{1}{N}$ либо $q < \frac{1}{N}$ , оставим читателю.

Также, при $p=q=\frac{1}{2}$ наблюдается равенство вероятностей для счётов 10-8, 10-9, 9-10, 8-10, и для счётов 3-5, 4-5, 5-4, 5-3. Покажем, что для любого $N \ge 2$ при $p=q=\frac{1}{2}$ вероятность счёта (N, N-2) равна вероятности счёта (N, N-1) .

Вероятность счёта (N, N-2) в данном случае есть $\binom{2N-3}{N-2} \frac{1}{2^{2N - 2}}$ , а вероятность счёта (N, N-1) есть $\binom{2N-2}{N-1} \frac{1}{2^{2N - 1}}$ .

Заметим, что $\binom{2N-2}{N-1}=\binom{2N-3}{N-2} \frac{2N-2}{N-1}=2\binom{2N-3}{N-2}$ .

Получаем, что $\binom{2N-2}{N-1} \frac{1}{2^{2N - 1}} = 2\binom{2N-3}{N-2}\frac{1}{2^{2N - 1}}=\binom{2N-3}{N-2}\frac{1}{2^{2N - 2}}$ .

Полученный результат легко объясняется с точки зрения модели: и для счёта (N, N-2) и для счёта (N, N-1) в серии матчей должен возникнуть счёт (N-1, N-2) после какого-то матча. Из этого счёта может с вероятностью $\frac{1}{2}$ получиться счёт , либо с вероятностью $\frac{1}{2}$ может получиться счёт (N-1, N-1) . Из последнего счёта возможен только счёт (N, N-1) или (N-1, N) с равными вероятностями.

Так, для формата FT2/BO3 получаем что действительно, если команды равны и исход матча определяется симметричной бернуллиевской монеткой, то вероятности счётов 2-0/0-2 и счётов 2-1/1-2 одинаковы и составляют $\frac{1}{2}$ каждый. Означает ли это, однако, что итоговый счёт для формата FT2/BO3 не позволяет извлечь совершенно никакой информации о силе команд и вероятностях победы?

Заметим, что полученные нами ранее формулы для вероятностей счёта позволяют найти ML-оценки вероятностей победы и . Вероятность счёта (x_1, x_2) пропорциональна произведению $p^{x_1} q^{x_2}$ . Логарифм правдоподобия, с точностью до постоянного слагаемого, есть $L = x_1 \ln p + x_2 \ln q = x_1 \ln p + x_2 \ln (1-p)$ . Дифференцируя логарифм правдоподобия по и приравнивая производную к нулю получаем условие экстремума: $\frac{x_1}{x_2} = \frac{p}{1-p}=\frac{p}{q}$ .

Отсюда следуют оценки на вероятности: $\hat{p}=\frac{x_1}{x_1 + x_2}$ , $\hat{q}=\frac{x_2}{x_1 + x_2}$ . Доказательство того, что эти оценки максимизируют логарифм правдоподобия, оставим читателю.

Таким образом, хоть формата FT2/BO3 и недостаточно для точной оценки относительной силы команд, однако некоторую информацию ML-подход всё-таки позволяет извлечь. Рассмотрим, как меняется функция правдоподобия для фиксированного счёта:

Вероятности для счётов 2-0 и 0-2 принимают максимум в точках, соответствующих однозначной победе соответствующей команды. Вероятности для счётов 2-1 и 1-2 принимают максимум в точках $p=\frac{2}{3}, q=\frac{1}{3}$ и $p=\frac{1}{3}, q=\frac{2}{3}$ соответственно, т.е. счёт с одной победой в серии проигравшей команды является более сильным свидетельством в пользу равенства команд, нежели счёт "в одни ворота". Как от вероятности зависит будет ли счёт "в одни ворота" или нет в формате FT2/BO3 ?

Вероятность счёта "в одни ворота" есть сумма вероятностей для счётов 2-0 и 0-2. Эта вероятность есть:

Вероятность счёта "не в одни ворота" есть сумма вероятностей для счётов 2-1 и 1-2. Эта вероятность есть:

Можно заметить, что счёты 2-1/1-2 могут выпадать при практически любом соотношении сил команд, кроме крайних случаев p=0, q=1 или p=1, q=0 . При увеличении равенства сил команд, т.е. при $p \to \frac{1}{2}$ , вероятность счётов 2-1/1-2 увеличивается, но она всегда ниже вероятности счётов 2-0/0-2 и становится равной только в точке своего максимума (и минимума вероятности 2-0/0-2), при $p=\frac{1}{2}$ . Т.е. проводя между фиксированными командами достаточно большое количество серий матчей в формате FT2/BO3, мы не увидим результатов 2-1/1-2 более чем в 50% серий матчей просто в силу того, что счёт "не в одни ворота" не выпадает чаще 50% независимо от силы команд. А в случае неравенства сил команд частоты счётов 2-1/1-2 будут даже меньше 50%. Факт выпадения счётов 2-1/1-2 свидетельствует в пользу равенства команд, тогда как факт выпадения счётов 2-0/0-2 говорят об обратном.

При проведении турнира у нас нет возможности посчитать частоты различных счётов, так как большинство серий матчей проводятся для каждой пары команд, т.е. для каждых вероятностей и , лишь один раз. Тем не менее, даже единственный сампл счёта позволяет извлечь информацию об относительной силе команд. Несмотря на то, что при равной силе команд счёты 2-0/0-2 выпадают с такой же частотой, что и счёты 2-1/1-2, это не говорит о том, что мы можем просто не учитывать факт выпадения тех или иных счётов. Чем больше счётов 2-1/1-2 мы получаем в турнире — тем больше у нас оснований полагать, что в условиях описанный выше модели силы команд, участвующих в турнире, действительно примерно равны.

Теги:

Хабы:

Математика

Вероятность счёта серии матчей в бернуллиевской модели

Сценарий

Вероятность определённого счёта в серии матчей

Результаты

Публикации

Истории

Ближайшие события