Приветствую Вас, уважаемые Читатели! Сегодня я хочу поговорить о таком геометрическом понятии, как конгруэнтность. В повседневной жизни мы его не используем, ведь куда проще говорить о равенстве, чем о такой трудновыговариваемой конструкции. Однако, в математике между ними есть отличие. Давайте на примерах!
Для начала возьмем два отрезка. В графическом редакторе они у меня получились с помощью "копировать-вставить". Что мы можем сказать о них?
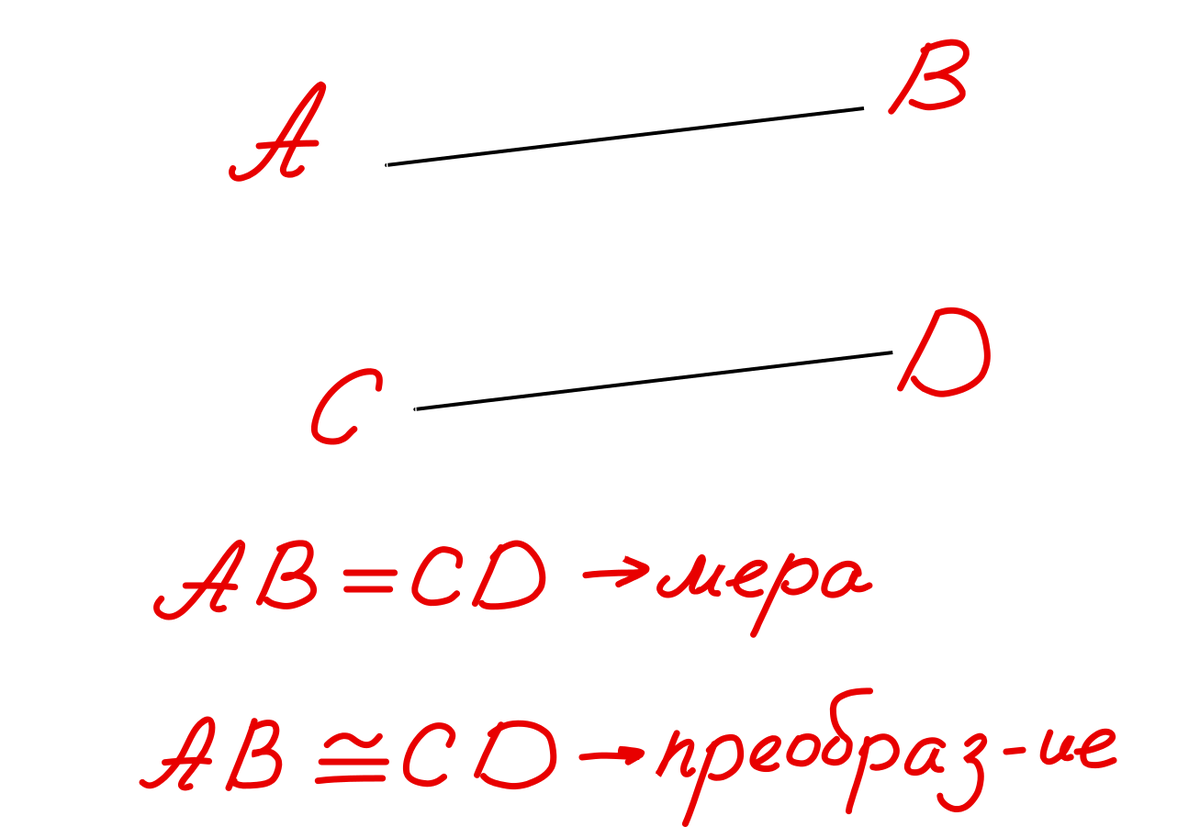
Когда мы говорим о "равенстве", мы предполагаем наличие некоторой меры, которая так или иначе сводится к числу. В нашем случае мерой является расстояние между точками или длина отрезка. В то же время мы можем говорить и о конгруэнтности отрезков, имея ввиду, что как геометрические фигуры (наборы точек) любой из отрезков можно получить из другого с помощью некоторого преобразования.
Например, в Евклидовой геометрии две фигуры называются конгруэнтными, если их можно взаимно получить из переноса, вращения и симметрии. Конгруэнтность определяется как отношение эквивалентности, обладающее свойствами рефлексивности, транзитивности и симметричности.
Теперь давайте перейдем к двумерным геометрическим фигурам. Очевидно, что треугольники, показанные на рисунке равны с точки зрения меры-площади и конгруэнтны, т.к. получены симметрией:

А что, если речь идёт о таком случае:

Здесь мера могла бы позволить нам говорить о равенстве площадей, но о конгруэнтности не может быть и речи. Однако же, если разрешить непрерывные деформации - сжатия и растяжения, все немного поменяется... В общем случае, конгруэнтность - это понятие, которое относится к теоретико-множественному представлению геометрических фи��ур. Апологетом этого подхода в СССР была знаменитый математик А.Н. Колмогоров.

Колмогоров вообще к определениям относился с большим вниманием. Например, категорически не любил понятие "равных" фигур (в том смысле, в котором его сейчас в школе используют), предпочитая определять их исключительно как "конгруэнтные". В качестве аргумента рисовал на доске два конгруэнтных треугольника А и B и говорил: "Ну как же эти фигуры могут быть равны? Если бы они были именно равны, то мы имели бы здесь A∩B = A = B. Это, очевидно, не так, ибо пересечение пусто A∩B = Ø!"

Этот подход, оказывается, применяется и в теории категорий, где можно отказаться от понятия равенства объектов, заменив их равенством т.н. стрелок между ними и введя понятие изоморфизма. Математика удивительна! Как здесь не вспомнить знаменитую фразу из Конституции США, написанной Томасом Джефферсоном: "Все люди равны между собой". Нет! Они создаются конгруэнтными. Они могут иметь равные права, но ни один человек не равен другому человеку.
