nulovkin 6 фев 2023 в 10:00

Простейшая нейросеть: еще раз и подробнее

10 мин

59K

Программирование*Математика*Параллельное программирование*Машинное обучение*

Обзор

Введение

Некоторое время назад, во время учебы в институте, я решил понять принцип работы нейросетей. Усвоить его на уровне, необходимом, чтобы написать небольшую нейросеть самостоятельно. Начать я решил с книги Тарика Рашида "Создай свою нейросеть". Эта статья представляет из себя краткий конспект этой книги для тех, кто, как и я, столкнулся с трудностями во время изучения этой темы и этого учебника (не в последнюю очередь благодаря проблемам редактуры). В процессе я надеюсь разложить все по полочкам еще раз. Предположу, что перемножение матриц и взятие производной никого из читателей не смутят и сразу пойду дальше.

Итак, машинное обучение это незаменимый инструмент для решения задач, которые легко решаются людьми, но не классическими программами. Ребенок легко поймет, что перед ним буква А, а не Д, однако программы без помощи машинного обучения справляются с этим весьма средне. И едва ли вообще справляются при минимальных помехах. Нейросети же уже сейчас решают многие задачи (включая эту) намного лучше людей. Их способность обучаться на примерах и выдавать верный результат поистине очаровывает, однако за ней лежит простая математика и сейчас я покажу это на примере перцептрона.

Описание работы нейронов

Перцептрон с тремя слоями по три нейрона

Каждый нейрон (или узел) принимает сигналы от узлов предыдущего слоя и передает на следующий. Каждая связь между нейронами имеет собственный вес.
Таким образом, входной сигнал узла 1 слоя 1 передается на узел 1 слоя 2 с коэффициентом $w_{11},$ на узел 2 слоя 2 с коэффициентом $w_{12}$ и так далее. Все сигналы, полученные узлом уровня 2 складываются. Это его входной сигнал. Таким образом сигналы передаются с уровня на уровень, до выхода.

Для того, чтобы результат был более предсказуемым, используется функция сглаживания, одна из самых популярных - сигмоида y=1/(1+e^-x).

Если каждый узел обрабатывает поступивший сигнал функцией сглаживания, то можно быть полностью уверенным, что он не выйдет за пределы от 0 до 1.

Таким образом, нейрон суммирует входные сигналы, умноженные на веса связей, берет сигмоиду от результата и подает на выход.

Еще раз, для всего слоя:

А как это решает задачу?

Итак, как же применить нейросеть для распознавания букв на картинке?

Входным сигналом для этой картинки 28 на 28 будет последовательность из 784 чисел от 0 до 255, каждое из которых шифрует цвет соответствующего пикселя. Итак, на входном уровне должно быть 784 узла.
Информация, которую нам необходимо получить на выходе это "какая цифра скорее всего на картинке". Всего 10 вариантов. Значит, на выходном уровне будет 10 узлов. Узел, на котором сигнал будет больше и будет ответом нейросети на задачу - например, для этой картинки в идеале все узлы выходного уровня должны показывать на выходе ноль, а пятый - единицу.
Добавим еще уровень, чтобы переход не был таким резким. Допустим, нейросеть будет из трех слоев - 784, 100 и 10 узлов. Общепринятого метода выбора точного количества узлов на промежуточных слоях и количества самих промежуточных слоев не существуют - разве что проводить эксперименты, и сравнивать результаты. В нашем случае первый уровень представляет пиксели входного изображения, третий - распознанные цифры а второй каким-то трудноотслеживаемым образом представляет закономерности, подмножества пикселей, которые свойственны разным цифрам.

Добавим матрицы

Переведем правила распространения сигнала на язык математики. Задача получить сигналы нового слоя, то есть "Умножить вес каждого узла слоя 1 на его выходную связь, ведущую к узлу слоя 2 и сложить" на удивление сильно подходит на описание умножения матриц. В самом деле, расположим в каждом столбце матрицы весов веса связей, исходящих из одного узла и умножим справа на столбец входных сигналов и получим выходной сигнал этого слоя в столбце получившейся матрицы.

Получение сигнала следующего уровня по формуле X = W*I

В строках же матрицы весов будут веса связей, ведущих в один узел нового слоя, каждый из которых умножается на вес порождающего его узла. Очень изящно! Разумеется, из-за правил перемножения матриц высота конечного столбца будет равна высоте матрицы весов, а высота матрицы входных сигналов -- ширине матрицы весов. Для перехода из первого слоя (784 узла) во второй (100 узлов) в матрице весов нашей задачи понадобится таблица в 100 строк и 784 столбца.
Итак, вся загадка заключается в том, какими именно значениями заполнена матрица весов. Ее заполнение называется тренировкой нейросети. Затем останется лишь опросить нейросеть, то есть решить конкретную задачу:

Подать на вход картинку, то есть столбец из 784 сигналов.
Умножить на него справа таблицу весов 12.
Применить сигмоиду для сглаживания результатов.
На результат справа умножить таблицу весов 23.
Применить сигмоиду.
Взять номер узла с наибольшим значением.

Таким образом, из 784 значений с помощью всего лишь двух матричных умножений и сглаживаний получилось 10 чисел в диапазоне от 0 до 1. Номер узла с самым большим из них это значение цифры на картинке, как ее распознала нейросеть. Насколько это соответствует истине, зависит от тренировки нейросети.

Тренировка. Обратное распространение ошибок

Метод обратного распространения ошибок это сердце нейросети. Его суть заключается в том, чтобы после получения значения ошибки на последнем слое передать правки на предыдущие слои.

Один из основных существующих подходов - распределять ошибку пропорционально весам связей.

Или то же самое, но для нескольких узлов на внешнем слое:

Обратное распространение ошибки с нескольких слоев

Ошибка, то есть e, это разница между t - желаемым значением и o - значением на выходном слое: .

Как мы видим, o1 высчитывается из узлов первого слоя с помощью связей w11 и w12, а значит, именно их и нужно корректировать с помощью ошибки этого узла. Новое значение w11 зависит от доли w11 в сумме связей, ведущих к узлу: $\frac{w11}{w11+w21}$ . Конечно, для w21 нужно заменить w11 в числителе на w21.

Теперь можно было бы приступить и к, собственно обратному распространению ошибки. Использовать данные следующего слоя для работы с предыдущим:

Однако, у нас нет целевых значений для скрытого слоя. Не беда. Просто сложим ошибки всех связей, исходящих из этого узла, и получим его ошибку!

Сложим, получим значение ошибки и просто повторим все еще раз. Пример показан ниже:

Еще раз, словами: Ошибку Oi умножаем на долю связи $w_{ki}/\sum_i W_i$ в сумме связи отдельного узла k со всеми узлами следующего уровня, чтобы получить ошибку узла k предыдущего слоя. Затем все ошибки связей из узла k складываем и получаем его собственную ошибку. И так далее.
Перепишем все вышесказанное в виде матриц:

Удобно. Но не до конца. Было бы здорово избавиться от всех этих отличающихся знаменателей. И деления. совсем не удобно делить тысячу узлов на тысячу разных сумм. Было бы здорово как-то все упростить. Тут нам поможет тот факт, что ~~для написания~~ ~~нейросети позволено забыть математику за третий класс~~ на практике у нас будет больше двух узлов в слое. И значение числителя (например 0,2, 0,4 или 0,9) гораздо важнее, чем значение знаменателя (например 9,7, 9,3 или 8,4). Что приводит нас к моему любимому моменту в книге. Нормирующий множитель? Да зачем он нам?

Здорово упрощенный расчет ошибки скрытого слоя

Мы получили донельзя простую формулу обратного распространения ошибки с помощью матрицы весов и ошибки наружного слоя. Обратите внимание, что столбцы матрицы весов здесь поменяны местами со строками и наоборот, то есть матрица транспонирована.

Однако, нужно держать в уме, что это просто иллюстрация для идеального случая и понимания концепции. В нашей нейросети все немного сложнее.

Тренировка. Обновление весов

Однако, нужно напомнить, что мы дважды применяем сигмоиду по мере расчета веса узла. Кроме того, представим, что на узле ошибка 0,3. Если мы изменим одну связь, ведущую к этому узлу, то изменение других связей может снова все испортить. А так быть не должно. Интуитивно кажется, что каждая связь должна меняться сообразно своей роли в ошибке. При этом эта роль это не просто доля веса, ведь мы дважды применяли сигмоиду!
Итак, нам нужно свести ошибку каждого узла к нулю. Ошибка зависит от множества переменных, каждая из которых влияет на результат по разному. Звучит как задача для производной!

Здесь нам пригодится метод градиентного спуска. Если нам известно, что связь Wij влияет на общую ошибку, то просто посчитаем производную и сделаем шаг в направлении нуля.

Нам нужно минимизировать ошибку. Значит, наш шаг должен вести нас к нулевой O . Нам нужно узнать соответствующую Wij. И выполнить это для каждой связи в узле, а затем для каждого узла в слое.

Рассмотрим это для нашей многомерной функции: нам нужно узнать такие значения W (такие координаты, только не на двумерной плоскости, а во множестве измерений. Но это не сильно все осложнить), чтобы значение O было минимальным (спуститься в самую глубокую яму на карте).
Напомню, что нужно делать все более мелкие шаги, чтобы не пройти центр "ямы". Для этого нужен специальный коэфициент, убывающий во время обучения.
Также вы можете подумать, что легко можно забрести в неправильную "яму", то есть ложный минимум:

К счастью, по какой-то причине для задач, подобных нашей, большинство ложных минимумов располагаются близко от основного и почти также глубоки. Сейчас можно об этом не беспокоиться.
Самое лучшее в методе градиентного спуска, это его устойчивость к ошибкам. Если попадется несколько ошибок в тренировочных данных, последующие примеры постепенно сгладят эффект.

Как на самом деле посчитать ошибку

Для начала, вспомним, что ошибиться можно в обе стороны. А значит, значения ошибок будут как отрицательные, так и положительные. Тогда сумма ошибок может оказаться не тем больше, чем больше ошибки, а просто близкой к нулю. Значит, e = t-o как значение ошибки использовать нельзя. Приходит на ум модуль: e = |t-o|, чтобы избежать отрицательных значений. Однако тогда функция будет вести себя странно в районе нуля. Лучший вариант из всех для оценки ошибки это .
Теперь, когда мы исправили проблему подсчета ошибок, попробуем посчитать производную.. Это выражение представляет изменение значения ошибки при изменении веса узла.

Перепишем функцию оценки ошибки:

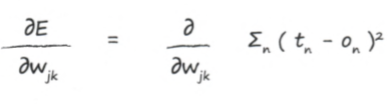
Получившееся выражение можно сразу упростить. Ошибка не зависит от всех значений на узлах, только от тех, что соединены с узлом k. Упростим выражение:

Воспользуемся цепным правилом дифференцирования сложных функций:

Теперь мы можем работать с частями этого уравнения по отдельности:

$\frac{dE}{do_k} = \frac{d(t_k-o_k)^2}{{do_k}} = -2(t_k-o_k)$

В осталось разобраться со второй частью, а первую подставим в общее уравнение:

Перепишем выходной сигнал в явном виде:

Мы заменили выходной сигнал на сумму произведений каждой из связей, ведущих к этому узлу, на вес узла-источника.

Вот формула, по которой дифференцируется сигмоида (и как хорошо, что нам не нужно это доказывать. Это работает):

Применим это к нашей формуле и получим:

Обратите внимание на то, что в последней формуле появился сомножитель (Одна из смущающих вещей в редактуре учебника. В этой формуле j под суммой и j в остальных местах, разумеется, разные, хотя оба представляют предыдущий уровень, так что здесь я обозначу индекс под суммой i. j находится в промежутке от 0 до i.):

$o_j=\frac{d(\sum_iw_{ik}*o_i)}{dw_{jk}}$ .

Это результат применения цепного правила дифференцирования сложной функции, то есть производная выражения в скобках сигмоиды. Возможно вы, как и я поначалу, не поняли, почему оно именно такое. Что ж, это значение представляет зависимость суммы всех связей с узлом k, умноженных на веса их узлов от веса одной связи. Поскольку производная суммы равна сумме производных, а все прочие веса кроме $w_{jk}$ относительно него считаются константами, то:

$\frac{d(\sum_iw_{ik}*o_i)}{dw_{jk}} = \frac{d(w_{jk}*o_j)}{dw_{jk}} = o_j * w_{jk}^0 = o_j$ .

Таким образом, окончательный вид функции для изменения узлов предпоследнего слоя это (еще раз, помните, что на картинках j под суммой это не тот же j, что и снаружи):

Градиент функции ошибки связей с выходным слоем

Чтобы таким же образом изменить узлы слоя до него, подставим нужные связи и заменим очевидную финальную ошибку на посчитанную ранее ошибку скрытого слоя

Градиент функции ошибки связей со скрытым слоем

Применим нашу формулу, отображая тот факт, что результат необходимо умножить на коэфициент обучения, а градиент по знаку противоположен изменению связей:

Перенесем W налево и покажем, как выглядят эти вычисления в матричной записи (коэфициент обучения для наглядности опущен), Е это значение ошибки узла, S это сумма произведений весов, ведущих к одному узлу, на их связь с этим узлом, на которую примененили сигмоиду, O это сигнал на выходе из предыдущего слоя:

Перепишем формулу целиком в удобном матричном виде (как можно было заметить в предыдущей формуле, последний сомножитель это транспонированная матрица выходных сигналов предыдущего слоя):

Эту формулу будет удобно использовать в коде.

Разбор примера обновления коэфициентов

Если вы не совсем поняли с первого раза, какие значения куда подставлять, то разберем такой пример:

Возьмем конкретно первый узел выходного слоя, где Мы хотим обновить весовой коэффициент $w_{11}$ для связи между последними двумя слоями. Вспомним формулу градиента ошибки:

Вместо подставим нашу ошибку

Сумма $\sum _jw_{jk}o_j$ в данном случае равна (2,0*0,4) + (3,0*0,5) = 2,3.

Сигмоида $1/(1+e^{-2,3}) = 0,909.$

Сигнал .

Следовательно, все значение в целом составит .
Допустим, что коэффициент обучения составляет 0,1. Тогда изменение веса составит -0,1*(-0,02647)=+0,002647. Это и есть тот довесок, который нам нужно добавить в связь $w_{11}$ . Новое значение ее веса составит 2,002647.
Еще несколько тысяч таких изменений и чаша наша полна.

Пара слов о подготовке данных

Как мы видим, при больших значениях входного сигнала значение сигмоиды будет изменяться очень слабо, вне зависимости от знака. Это будет означать, что нейросеть почти не будет изменяться и веса останутся после обучения почти такими же. Значит, весовые коэфициенты должны располагаться поближе к нулю (но не слишком, это может вызвать проблемы с подсчетами из-за ограничений формата с плавающей точкой). Нам хорошо подойдет масштабирование входных сигналов от 0,0 до 1,0 - еще и потому, что именно такие сигналы обеспечивает сигмоида. Значение никогда не выдет за пределы (0;1).

Для работы нейросети необходимо указать начальные значения весовых коэффициентов. Причем, это не могут быть нули или просто одинаковые значения - в таких условиях они получат одинаковые правки и останутся совпадающими после обучения, что явно не даст нам хороших результатов. Остается указать случайные значения в приемлемом диапазоне, например от -1,0 до +1,0. Однако очевидно, что если значения весов в начале обучения будут близки к максимальным, то нейросеть может быстро насытиться. Это рассуждение, подкрепленное наблюдениями, породило эмпирическое правило: весовые коэффициенты должны выбираться из диапазона, приблизительно оцененного обратной величиной корня из количества связей, ведущих к узлу. Если к узлу ведут 3 связи, его вес должен быть случайным значением в промежутке $(0;\frac{1}{\sqrt3})$ .

Итоги

Эта статья, представляющая конспект-пересказ книги Тарика Рашида "Создай свою нейросеть" призвана объяснить некоторые детали того, как проектируется и работает простой перцептрон и обратное распространение ошибок в нем. Я написал ее для того, чтобы охватить всю картину вместе, однако даже после столь внимательного погружения в материал и прояснения каждой его части я не уверен, что смогу написать что-то похожее, например распознавалку знаков, без заглядывания в книгу. Однако, я намного ближе к этому, чем какое-то время назад.
Я надеюсь, что эта статья поможет таким же как я новичкам в мире нейросетей, кто не понял все аспекты процесса с первого раза и забросил книгу на пару лет.

Я приветствую критику как от них, так и от всех остальных, касательно фактических ошибок, стиля подачи материала, неточностей, упущений и других проблем статьи, которые, я уверен, найдутся, поскольку раньше я ничего подобного не писал.
Спасибо вам всем!

Теги:

Хабы: