Ряд Фибоначчи
Чи́сла Фибона́ччи (вариант написания — Фибона́чи[2]) — элементы числовой последовательности
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),
в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел[3]. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)[4].
- Википедия


Ряд Фибоначчи часто упоминается на собеседованиях, потому что в нем демонстрируется множество мощных методов, включая рекурсию. Он является отличным примером того, что мы называем мемоизацией(запоминанием). Понимание ряда Фибоначчи и его работы очень полезно.
Математически ряд Фибоначчи представляет собой последовательность чисел, которые следуют этому уравнению: F(n) = F(n-1) + F(n-2). Эта последовательность встречается в различных интересных контекстах, например, в природе, в раковинах, спиральных структурах и галактиках, а также в дизайне римских полов, и даже брокеры используют ряд Фибоначчи для прогнозирования акций.
func fib(_ n: Int) -> Int { if n == 0 { return 0 } else if n == 1 { return 1 } else { return fib(n - 1) + fib(n - 2) } }
В коде серия Фибоначчи выглядит следующим образом: для F(0) и F(1) возвращаем их значения напрямую, а затем алгоритм сводится к этой строке - return fib(n-1) + fib(n-2). Это является ключевым моментом алгоритма и демонстрирует использование рекурсии.
Однако у ряда Фибоначчи есть проблема: с увеличением чисел в последовательности алгоритм требует все больше времени для вычисления. Это связано с тем, что время, необходимое для вычислений, растет экспоненциально, и сложность алгоритма составляет O(2^n). Это делает вычисления очень затратными.
Наша задача - найти способ оптимизировать этот алгоритм и сделать его быстрее. Именно здесь на помощь приходит мощная техника, известная как мемоизация, которую важно знать и понимать.
Мемоизация
Чтобы понять мемоизацию, нужно рассмотреть проблему с рядом Фибоначчи. Для простых чисел, таких как число до F(5), ряд Фибоначчи вычисляется достаточно быстро. Однако, при вычислении чисел более высокого порядка, повторное вычисление чисел становится очень затратным по времени.
Мемоизация - это техника оптимизации, ускоряющая алгоритмы за счет кэширования или хранения результатов вычислений для их использования в будущих вычислениях. В случае ряда Фибоначчи, мы можем создать словарь (назовем его "Memo") для хранения ранее вычисленных чисел. Затем, когда мы вычисляем каждое число ряда Фибоначчи, мы сохраняем результат в массиве и возвращаем его. Таким образом, в следующий раз нам не нужно вычислять это число снова и снова.
var memo = [Int: Int]() func fib(_ n: Int) -> Int { if n == 0 { return 0 } else if n == 1 { return 1 } if let result = memo[n] { return result } memo[n] = fib(n - 1) + fib(n - 2) return memo [n]! }
Благодаря мемоизации, эффективность алгоритма возрастает значительно. Теперь вместо того, чтобы за 19 секунд вычислить ряд Фибоначчи из 30 чисел, мы можем вычислить тысячи чисел. Это увеличение на 3333%. Мы превратили алгоритм из экспоненциального (O(2^n)) в линейный (O(n)).
Именно поэтому ряд Фибоначчи и мемоизация являются отличными примерами для интервью. Они объединяют рекурсию и мемоизацию, показывая, как сделать затратный алгоритм быстрее. Знание и понимание ряда Фибоначчи и мемоизации помогут вам решать подобные задачи быстро и эффективно.
import UIKit func fibNaive(_ n: Int) -> Int { print(n) if n == 0 { return 0 } else if n == 1 { return 1 } else { return fibNaive(n - 1) + fibNaive(n - 2) } } fibNaive(20) // 20 = 13s / 22 = 54 s var memo = [Int: Int]() func fib(_ n: Int) -> Int { if n == 0 { return 0} else if n == 1 { return 1 } if let result = memo[n] { return result } memo[n] = fib(n - 1) + fib(n - 2) return memo[n]! } fib(22) // 90 max
Что касается создания одного из них с нуля, то это очень просто. Представляю к вашему вниманию две реализации: одну наивную, которая ничего не запоминает и не хранит, и вторую, где мы используем мемоизацию и храним наши результаты по мере их вычисления.
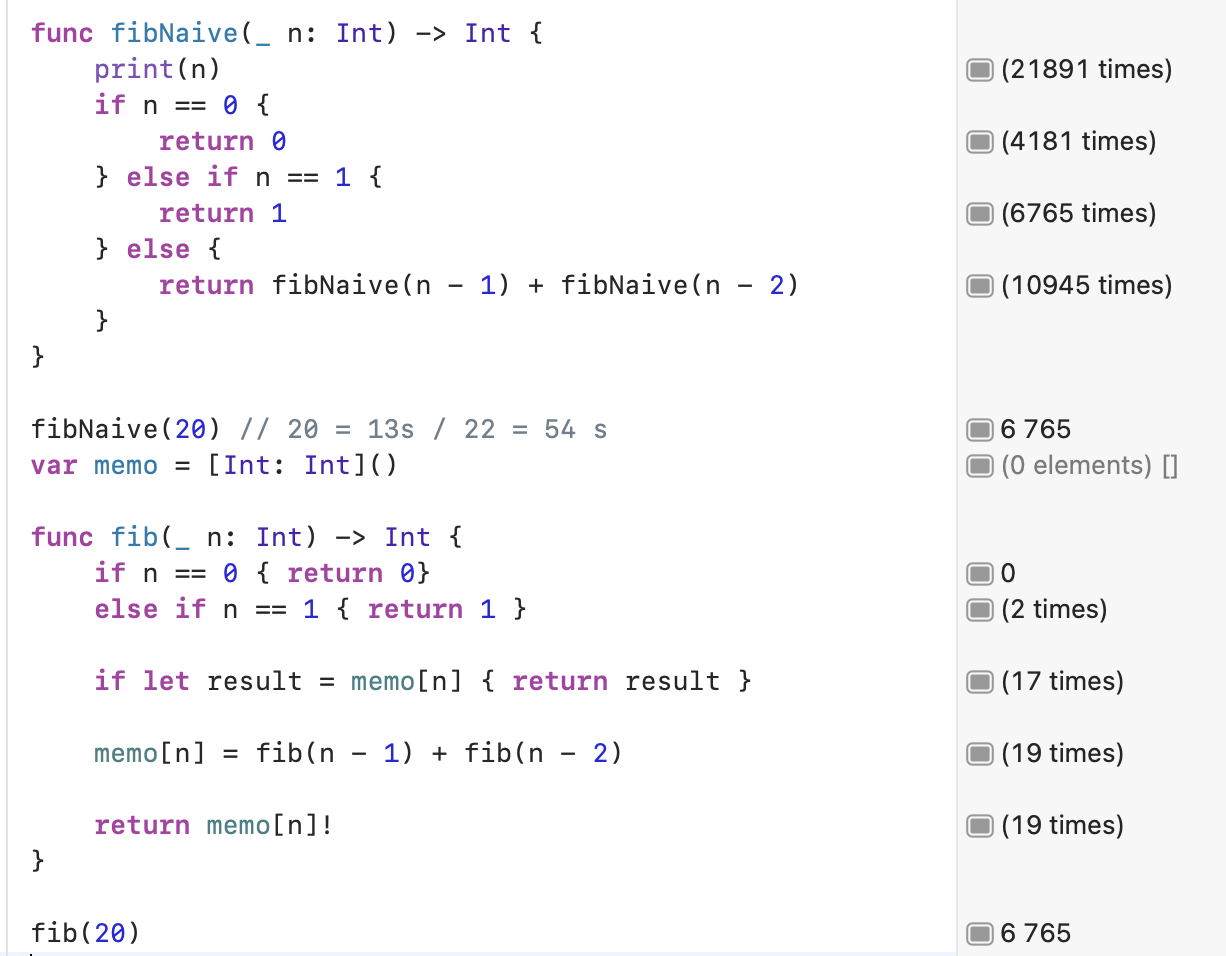
На мгновение остановимся на мемоизированном варианте, чтобы показать, сколько времени требуется для выполнения очень маленького вычисления Фибоначчи для числа 20. Если мы запустим его для простого числа, например, 20, вы увидите, что счетчик работает, пересчитывая одни и те же числа снова и снова. В среднем это занимает около 13 секунд, что не так уж и много. Теперь, если я увеличу его на один или два, это займет еще больше времени. Это экспоненциальный рост, увеличивающийся в размерах, и для очень маленьких приращений числа требуется все больше и больше времени. Именно так работает ряд Фибоначчи, и именно поэтому он так затратен.
Теперь давайте сравним это с мемоизированной версией и посмотрим, каково это - хранить эти значения. Во втором случае мы будем хранить наши результаты в словаре. Каждый раз, когда мы вычисляем F(n-1) + F(n-2), мы будем хранить его в ключе, представленном N, каким бы ни было число в этот момент (20, 21, 22 и т. д.). Мы просто сохраним этот результат. Затем, по мере выполнения последовательных вычислений, если мы можем извлечь результат из словаря, мы просто вернем его, не вычисляя его снова.
Заключение:
Это удобно не только для рядов Фибоначчи, но и для всего, что связано с дорогостоящими вычислениями, которые можно сохранить, кэшировать и использовать в будущих результатах.
В этом и заключается сила мемоизации.
Она используется для самых разных вещей.
Ряд Фибоначчи - отличный пример. Когда дело доходит до реального интервью.
Я слышал, как людей просили воспроизвести ряд Фибоначчи.
Это не огромный алгоритм, он сводится к одной строчке и двум случаям: конец равен нулю и единице. Но мой совет - просто запомните эту строчку, потому что она демонстрирует такую вещь как рекурсия.
Как только вы это пойме��е, очень просто перейти к мемоизированному примеру, где вы сможете продемонстрировать как взять трудозатратный алгоритм и сделать его более эффективным. Вы знаете - это называется мемоизацией.
