neshkeev 15 авг 2023 в 06:06

Обработка больших и очень больших графов: Pregel

Средний

24 мин

1.8K

Алгоритмы*Apache*Распределённые системы*

Обработка больших и очень больших графов:

Введение
Pregel

DISCLAIMER

Статья преследует цель реализации алгоритмов обработки графов на Apache Spark, которые в силу своего большого размера невозможно обработать классическими алгоритмами на одной машине. Оптимизация производительности реализованных алгоритмов выходит за рамки текущей статьи.

TLDR

Статья является продолжением предыдущей статьи в рамках цикла статей, посвященных обработке больших и очень больших графов. В статье реализованы распределенные версии четырех классических алгоритмов: "Связные компоненты", "Кратчайшее расстояние", "Топологическая сортировка" и PageRank на Apache Spark DataFrame API. Алгоритмы составлены в соответствии с идеями популярного фреймворка распределенной обработки графов Pregel.

Мотивация

В предыдущей статье было дано теоретическое описание трех фреймворков для обработки: Pregel, GraphLab, PowerGraph. Настало время для практической реализации, и первым на очереди будет Pregel.

Обзор фреймворка Pregel

Перед разбором практической части, необходимо вспомнить основные концепции фреймворка.

Если разложить фреймворк Pregel по четырем измерениям, то можно характеризовать его следующим образом:

программная модель: вершинно-центричная,
модель исполнения: синхронная,
способ синхронизации: обмен сообщений,
разбиение графа: по ребрам (edge-cut).

Вершинно-центричная программная модель

Реализованные алгоритмы запускаются на каждой вершине одновременно. В алгоритмах можно использовать только то, что доступно вершине напрямую: значение вершины, смежные рёбра, веса рёбер и т.д.

Такой подход именуют "думай как вершина" (think like a vertex). Разработанный алгоритм много раз запускается на каждой вершине до тех пор, пока он не сойдётся. Один запуск алгоритма на вершине называется superstep - шаг.

Синхронная модель исполнения

Вычисление результата на графах обычно включает в себя четыре стадии:

запуск алгоритма на всех вершинах одновременно,
сбор результатов,
синхронизация результатов,
обновление состояния (данных в графе).

Фреймворк Pregel следует синхронной модели исполнения, что означает, что каждая стадия выполняется строго после предыдущей: пока алгоритм не завершится на всех вершинах, исполнение не перейдет к стадии сбора результатов и т.д.

Обмен сообщениями

Обмен сообщениями является центральной идеей фреймворка Pregel: разработанный алгоритм выполняется на каждой вершине, результаты которого отправляются всем смежным вершинам по отношению к исходящим ребрам. Важно учитывать, что отправка сообщений смежным вершинам по отношению к входящим ребрам невозможна: поток данных идет только в одном направлении.

Разбиение графа

Фреймворк Pregel полагается на разбиение графа по рёбрам. Такой подход ведет к перекосу (skew) данных при обработке power-law графов, которых в реальном мире большинство. На практике удобнее использовать разбиение по вершинам: одна вершина может присутствовать в нескольких подграфах. Разбиение графа на подграфы по вершинам тривиально: достаточно просто разделить множество ребер на непересекающиеся подмножества.

На картинке ниже представлено разбиение множества ребер на три непересекающихся подмножества. Так же можно заметить, что вершины 4 (красный) и 6 (синий) находятся в разных подмножествах:

Пример разбиения графа на подграфы по вершинам

Практическое применение

Программный Интерфейс Pregel

Хотя весь код будет реализован в декларативном виде на базе Apache Spark DataFrame API запросов, ниже приведен программный интерфейс фреймворка Pregel на Python. Императивный вариант распределенных алгоритмов на графах на Pregel будут демонстрироваться при помощи указанного API.

class PregelVertex(Protocol[VertexValue, EdgeValue, MessageValue]):

    @abstractmethod
    def compute(self, messages: List[MessageValue]) -> None:
        ...

    @abstractmethod
    def send_message(self, target_vertex_id, message: MessageValue):
        ...

    @abstractmethod
    @property
    def value(self) -> VertexValue:
        ...

    @abstractmethod
    @value.setter
    def value(self, new_value: VertexValue) -> None:
        ...

    @abstractmethod
    def out_edges(self) -> List[EdgeValue]:
        ...

Пояснения:

PregelVertex представляет собой абстракцию над вершиной графа, которая имеет три типовых параметра:
1. VertexValue тип данных, которые могут храниться в вершине,
2. EdgeValue тип данных для абстракции над ребрами;
3. MessageValue тип данных передаваемых сообщений.
метод compute принимает на вход список сообщений и вычисляет новое значение, которое сохраняется внутри текущего объекта,
метод send_message отправляет сообщение указанной вершине,
метод value представляет собой property для доступа к текущему значению,
метод out_edges позволяет получить список исходящих из текущей вершины ребер.

Оригинальная публикация допускает отправку сообщений произвольным вершинам. Концептуально, если отправлять сообщения несуществующим вершинам, то можно создавать новые вершины. На практике список адресатов составляют только из списка непосредственных соседей. Такое ограничение позволяет применять более эффективные алгоритмы разбиения графов с учетом локальности данных.

Задача "Связные компоненты" (Connected Components)

Решение задачи поиска связных компонент позволяет разбить граф на подграфы, между которыми нет связей (Wikipedia). Иными словами, можно разбить вершины и ребра графа на непересекающиеся множества. В результате каждая вершина должна быть помечена тегом, который позволяет определить ее принадлежность к определенному подграфу.

Императивный алгоритм

Алгоритм на Pregel выглядит следующим образом:

class CCPregelVertex(PregelVertex[int, Tuple[CCPregelVertex, CCPregelVertex], int]):

    def __init__(self, id: int):
        self.id = id
        self.value = id

    def compute(self, messages: List[int]) -> None:
        min_message_value = min(messages)

        if self.value > min_message_value:
            self.value = min_message_value

            for _, target in self.out_edges():
                self.send_message(target.id, self.value)

Комментарии к коду:

CCPregelVertex наследует PregelVertex, где типовые параметры:
1. int - тип значения, т.е. номер компонента связности/подграфа, к которому относится текущая вершина;
2. Tuple[CCPregelVertex, CCPregelVertex] - тип ребра в формате: (исходная вершина, конечная вершина);
3. int - тип сообщения, т.е. номер подграфа, в котором должны жить соседние вершины.
изначально предполагается, что в графе нет ребер, а значит каждая вершина является компонентом связности/подграфом;
метод compute корректирует номер подграфа, в котором находится текущая вершина:
1. на вход приходят сообщения, которые были отправлены текущей вершине;
2. выполняется поиск минимального сообщения;
3. минимальное сообщение сравнивается с текущим значением - минимальное из двух будет являться номером подграфа, который содержит текущую вершину;
4. если значение в текущей вершине было обновлено, то оповестить об этом соседей.
реализация остальных методов исключена, т.к. по большей части зависит от окружения.

Процесс вычисления конечного результата является итеративным (планировщик выполняет superstep много раз), и программист сам должен управлять сходимостью алгоритма и прервать его, когда полученный результат будет устраивать. В худшем случае (когда граф - это связный список без циклов) количество необходимых шагов (superstep) будет линейно зависеть от диаметра самой большой связной компоненты.

ПРИМЕЧАНИЕ: Если граф является направленным, то необходимо дополнить список рёбер рёбрами, которые идут в обратном направлении, т.к. для поиска компонентов связности необходимо распространять информацию и в прямом, и в обратном направлении.

Алгоритм на Apache Spark

Решение для Apache Spark строится на базе Spark DataFrame API запроса. Для исключения дублирования кода, основной алгоритм вынесен в функцию pregel_cc (подробные комментарии ниже):

def pregel_cc(edges: DataFrame, values: DataFrame, steps: int) -> DataFrame:
    result_df = values

    for i in range(1, steps + 1):
        result_df = (
            edges.join(result_df, col("src") == col("id"))
                .select(col("dst").alias("id"), col("value").alias("message"))
                .groupBy(col("id")).agg(F.min("message").alias("message"))
                .join(result_df, "id", "right")
                .select("id", F.least("message", "value").alias("value"))
        )
        if i % 5 == 0:
            result_df = result_df.checkpoint()

    return result_df

Комментарии к коду:

функция pregel_cc принимает на вход три параметра:
1. edges - датафрейм с ребрами графа. В датафрейме обязательно должны быть две колонки:
  - src - исходная вершина,
  - dst - конечная вершина.
2. values - датафрейм с вершинами графа. В датафрейме обязательно должны быть две колонки:
  - id - идентификатор вершины,
  - value - сохраненное в вершине значение.
3. steps - количество шагов (superstep), которое необходимо выполнить, чтобы алгоритм сошёлся.
result_df - датафрейм, который аккумулирует в себе результирующий план запроса;
каждые пять шагов (superstep) управляющая программа будет вычислять накопленный план.

Рассмотрим запрос поближе и укажем на аналогии с кодом на Python для вычисления связных компонент:

edges.join(result_df, col("src") == col("id")) позволяет соединить датафреймы ребер и вершин, так в результате появятся как минимум четыре колонки:
1. src - исходная вершина;
2. dst - конечная вершина;
3. id - идентификатор вершины (равен src);
4. value - текущее значение вершины (src и id). Это значение нужно отправить всем вершинам dst. В самом начале оно равно значению из колонки id.
.select(col("dst").alias("id"), col("value").alias("message")) формирует сообщение для каждой вершины. Фактически программа говорит: сейчас у вершины src значение value, каждая вершина dst должна об этом знать. На рисунке ниже можно найти соответствие этой инструкции коду для вычисления связных компонент на Pregel:

.groupby(col("id")).agg(F.min("message").alias("message")) позволяет вычислить итоговое сообщение. Вершина dst может получить много сообщений от разных src вершин, а значит необходимо выбрать из сообщений минимальное значение;

.join(result_df, "id", "right") позволяет соединить итоговые сообщения с датафреймом, в котором находятся текущие значения. Как минимум в итоге получится три колонки:
1. id - идентификатор текущей вершины,
2. value - текущее значение вершины,
3. message - итоговое сообщение от всех соседей. Нужно проверить меньше ли оно, чем текущее значение value.
.select("id", F.least("message", "value").alias("value")) позволяет вычислить итоговое значение:
1. id - текущая вершина,
2. F.least("message", "value") - выбрать минимум между сообщением и текущим значением,
3. .alias("value") - заменить текущее значение value в вершине id на вычисленное.

result_df = (...) позволяет актуализировать значения вершин. Эта операция аналогична рассылке сообщений, но со всех вершин и сразу всем.

Пример работы

Граф, представленный на картинке выше содержит две связные компоненты:

вершины {1,2,3,4,5},
вершины {6}.

Приведенный граф можно сгенерировать при помощи следующей функции:

def small_graph():
    """Generates a small graph for tests"""
    vertices = [ (x,) for x in range(1, 7) ]
    vertices_df = (
        spark
            .createDataFrame(vertices)
            .toDF("id")
    )
    edges = [ (1, 2, 1), (1, 3, 5), (2, 3, 1), (3, 4, 1), (4, 5, 1), (6, 6, 1) ]
    edges_df = (
        spark
            .createDataFrame(edges)
            .toDF("src", "dst", "weight")
    )
    return edges_df, vertices_df

Подготовка данных:

edges_df, vertices_df = small_graph()

Проследим как меняются значения в вершинах:

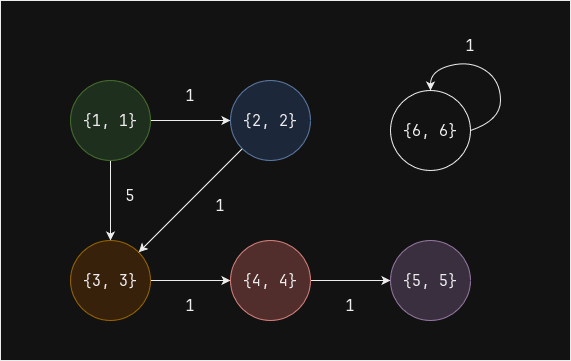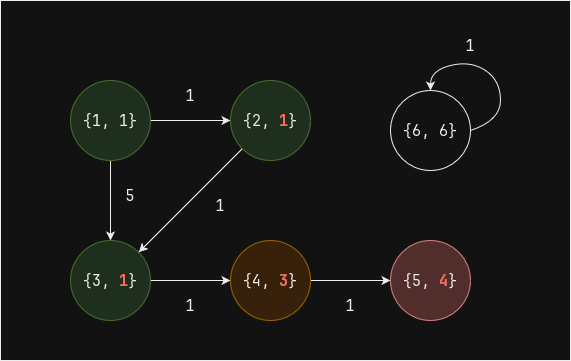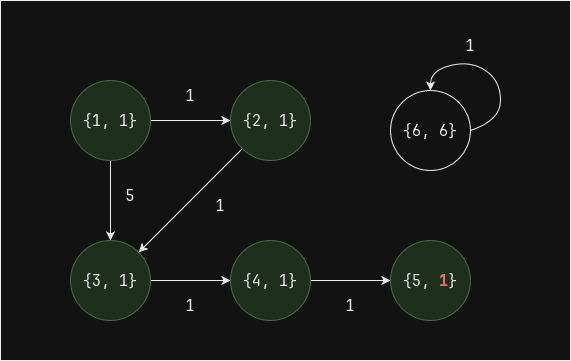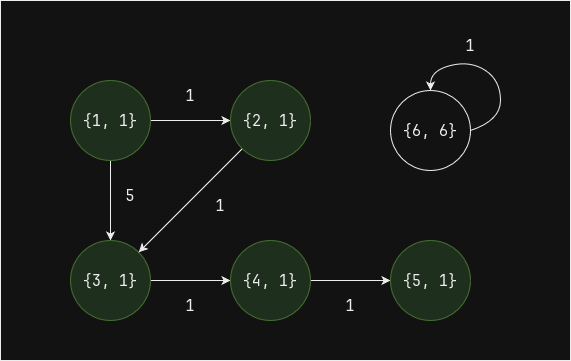
Начальное состояние - каждая вершина является компонентом связности/подграфом:

pregel_cc_df = vertices_df.withColumn("value", col("id"))
pregel_cc_df.show()

Выполним один шаг (superstep) - вершины 2 и 3 напрямую связаны с вершиной 1, поэтому для них значение value равно 1:

pregel_cc_df = pregel_cc(edges_df, pregel_cc_df, 1)
pregel_cc_df.show()

Выполним еще один шаг (superstep) - вершина 4 напрямую связана с вершиной 3, до нее дошло значение value равное 1:

pregel_cc_df = pregel_cc(edges_df, pregel_cc_df, 1)
pregel_cc_df.show()

Выполним еще один шаг (superstep) - вершина 5 напрямую связана с вершиной 4, до нее дошло значение value равное 1:

pregel_cc_df = pregel_cc(edges_df, pregel_cc_df, 1)
pregel_cc_df.show()

Выполним еще один шаг (superstep) - изменений больше нет, алгоритм сошёлся:

pregel_cc_df = pregel_cc(edges_df, pregel_cc_df, 1)
pregel_cc_df.show()

Таким образом, получилось два компонента связности: 1 и 6.

Замечания

Стоит заметить, что нумерация компонентов связности не обязательно монотонно возрастает на единицу: компоненты связности используют в качестве своих идентификаторов значение идентификатора одной из вершин, входящих в подграф. Этот факт необходимо учитывать, если нужно будет посчитать общее число компонентов связности или выполнить другую аналитику при помощи этой информации.

Реализованный алгоритм останавливается только, когда определенное количество шагов было выполнено. Заинтересованный читатель может реализовать остановку алгоритма по отсутствию новых сообщений самостоятельно. Для этого необходимо добавить новую колонку типа boolean под именем value_changed, значение которой необходимо установить в True, если F.least("message", "value") != col("value"). Когда алгоритм сойдется, изменений значения колонки value не будет, а следовательно, все строки будут иметь значение False в колонке value.

Задача о кратчайшем расстоянии (Single Source Shortest Path)

Решение задачи о кратчайшем расстоянии позволяет найти минимальное расстояние от одной из вершин графа до всех остальных вершин (Wikipedia). В результате в каждой вершине будет храниться сумма всех весов ребер, которые составляют кратчайший путь до текущей вершины от заданной вершины.

Императивный алгоритм

Алгоритм на Pregel выглядит следующим образом:

class MinDistPregelVertex(PregelVertex[int, Tuple[MinDistPregelVertex, MinDistPregelVertex, int], int]):

    def __init__(self, id: int, start_vertex_id: int):
        self.id = id
        self.value = 0 if id == start_vertex_id else sys.maxsize // 2

    def compute(self, messages: List[int]) -> None:
        min_dist_message_value = min(messages)

        if self.value > min_dist_message_value:
            self.value = min_dist_message_value

            for _, target, weight in self.out_edges():
                self.send_message(target.id, self.value + weight)

Комментарии к коду:

MinDistPregelVertex наследует PregelVertex, где типовые параметры:
1. int - тип значения, т.е. сумма весов ребер до текущей вершины от заданной вершины;
2. Tuple[MinDistPregelVertex, MinDistPregelVertex, int] - тип ребра в формате: (исходная вершина, конечная вершина, вес ребра);
3. int - тип сообщения, т.е. сумма весов ребер до соседних вершин.
в конструктор передаются два параметра:
1. идентификатор текущей вершины,
2. идентификатор вершины, от которой необходимо вычислить кратчайшее расстояние до текущей вершины. Возможны два варианта:
  - если текущая вершина является начальной вершиной, то кратчайшее расстояние будет равно нулю,
  - в противном случае начальное значение расстояния считается равным sys.maxsize // 2 (бесконечности). Такое значение выбрано, чтобы не допустить переполнения целочисленного типа.
метод compute корректирует значение весов ребер кратчайшего расстояния до текущей вершины от заданной:
1. на вход приходят сообщения, которые были отправлены текущей вершине;
2. выполняется поиск минимального сообщения;
3. минимальное сообщение сравнивается с текущим значением - минимальное из двух будет являться значением кратчайшего расстояния до текущей вершины;
4. если значение в текущей вершине было обновлено, то отправить соседям сообщение состоящее из суммы нового значения и значения веса до соседней вершины.
реализация остальных методов исключена, т.к. по большей части зависит от окружения.

Процесс вычисления конечного результата так же является итеративным (планировщик выполняет superstep много раз), и программист сам должен управлять сходимостью алгоритма и прервать его, когда полученный результат будет устраивать. В худшем случае (когда граф - это связный список без циклов) количество необходимых шагов (superstep) будет линейно зависеть от диаметра самой большой связной компоненты.

Алгоритм на Apache Spark

Решение для Apache Spark строится на базе DataFrame API запроса. Для исключения дублирования кода, основной алгоритм вынесен в функцию pregel_min_dist (подробные комментарии ниже):

def pregel_min_dist(edges: DataFrame, values: DataFrame, steps: int) -> DataFrame:
    result_df = values

    for i in range(1, steps + 1):
        result_df = (
            edges.join(result_df, col("src") == col("id"))
                .select(col("dst").alias("id"), F.expr("dist + weight").alias("message"))
                .groupBy(col("id")).agg(F.min("message").alias("message"))
                .join(result_df, "id", "right")
                .select("id", F.least("message", "dist").alias("dist"))
        )
        if i % 5 == 0:
            result_df = result_df.checkpoint()

    return result_df

Комментарии к коду:

на вход приходит 3 параметра:
1. edges - датафрейм с рёбрами графа. В датафрейме обязательно должны быть колонки:
  - src - исходная вершина,
  - dst - конечная вершина,
  - weight - вес ребра.
2. values - датафрейм с вершинами графа. В датафрейме обязательно должны быть колонки:
  - id - идентификатор вершины,
  - dist - значение минимального расстояния до текущей вершины.
3. steps - количество шагов (superstep), которое необходимо выполнить, чтобы алгоритм сошёлся.
каждые пять шагов управляющая программа (драйвер) будет запускать план на исполнение.

Рассмотрим запрос поближе и укажем на аналогии с кодом на Python для вычисления связных компонент:

edges.join(result_df, col("src") == col("id")) позволяет соединить датафреймы ребер и вершин, так в результате появятся как минимум пять колонок:
1. src - исходная вершина;
2. dst - конечная вершина;
3. id - идентификатор вершины (равен src);
4. weight - вес ребра от вершины src до вершины dst;
5. dist - текущее значение вершины (src и id). Сумму этого значения и веса ребра (weight) до соседней вершины нужно отправить всем вершинам dst.
.select(col("dst").alias("id"), F.expr("dist + weight").alias("message")) формирует сообщение для каждой вершины. Фактически программа говорит:
- сейчас у вершины src значение dist,
- вес ребра от src до dst равен weight,
- каждая вершина dst должна знать о значении dist + weight
На рисунке ниже можно найти соответствие этой инструкции коду для вычисления связных компонент на Pregel:

.groupby(col("id")).agg(F.min("message").alias("message")) позволяет вычислить итоговое сообщение. Вершина dst может получить много сообщений от разных src вершин, а значит необходимо выбрать из сообщений минимальное значение;

.join(result_df, "id", "right") позволяет соединить итоговые сообщения с датафреймом, в котором находятся текущие значения. Как минимум в итоге получится три колонки:
1. id - идентификатор текущей вершины,
2. dist - текущее значение вершины,
3. message - итоговое сообщение от всех соседей. Нужно проверить меньше ли оно, чем текущее значение dist.
.select("id", F.least("message", "dist").alias("dist")) позволяет вычислить итоговое значение:
1. id - текущая вершина,
2. F.least("message", "dist") - выбрать минимум между сообщением и текущим значением,
3. .alias("dist") - заменить текущее значение dist в вершине id на вычисленное.

result_df = (...) позволяет актуализировать значения вершин. Эта операция аналогична рассылке сообщений, но со всех вершин и сразу всем.

Пример работы

Приведенный граф тот же самый, который использовался в алгоритме поиска связных компонент. Минимальное расстояние будет вычисляться относительно вершины 1.

Подготовка данных

Функция get_min_dist_init_df позволит проинициализировать колонку dist по принципу:

если идентификатор текущей вершины равен идентификатору стартовой вершины, то кратчайшее расстояние равно 0,
в противном случае значение вершины равно sys.maxsize // 2 (бесконечность). Такое значение выбрано, чтобы не выйти за границы целого числа.

def get_min_dist_init_df(values: DataFrame, start: int = 1) -> DataFrame:
    return values.withColumn("dist",
        F.when(
            col("id") == F.lit(start),
            F.lit(0)
        )
        .otherwise(F.lit(sys.maxsize // 2))
    )

edges_df, vertices_df = small_graph()
min_dist_df = get_min_dist_init_df(vertices_df, start=1)

Проследим как меняются значения в вершинах:

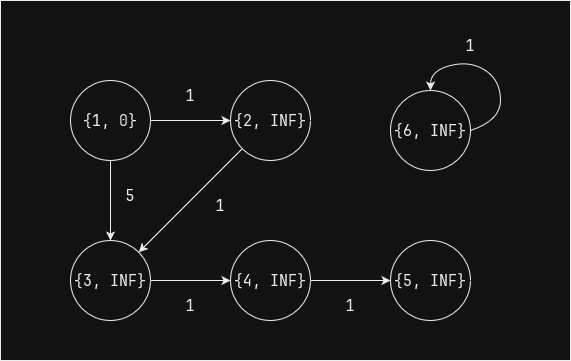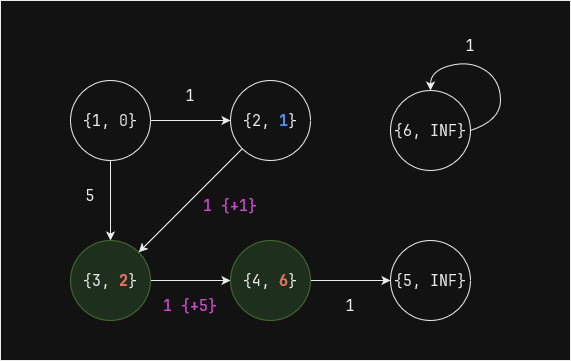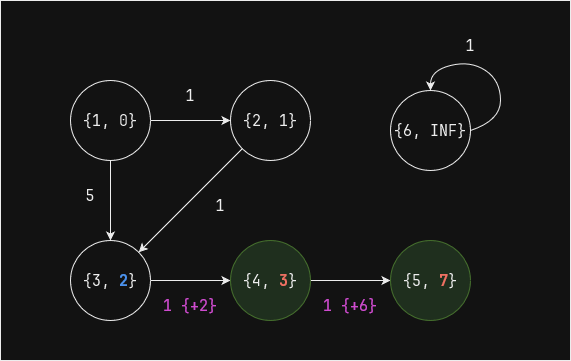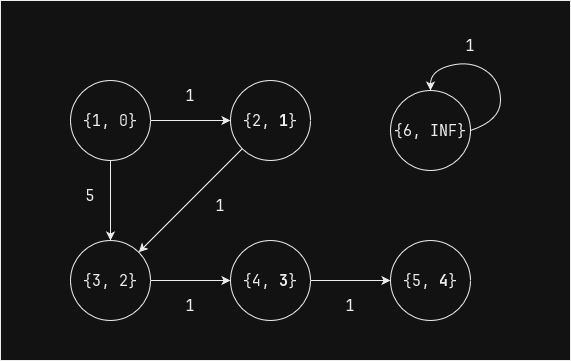
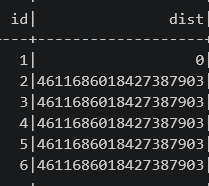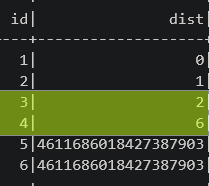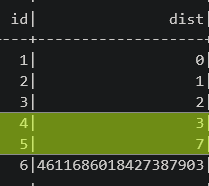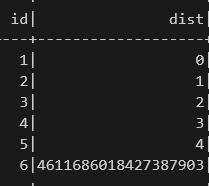
Начальное состояние - значение вершины 1 равно 0, значение остальных - бесконечность:

min_dist_df.show()

Выполним один шаг (superstep) - вершины 2 и 3 напрямую связаны с вершиной 1, поэтому для них значение dist изменяется:

min_dist_df = pregel_min_dist(edges_df, min_dist_df, 1)
min_dist_df.show()

Выполним еще один шаг (superstep) - вершина 3 связна с вершиной 2, а вершина 4 напрямую связана с вершиной 3, поэтому их значение dist изменяется:

min_dist_df = pregel_min_dist(edges_df, min_dist_df, 1)
min_dist_df.show()

Выполним еще один шаг (superstep) - вершина 5 напрямую связана с вершиной 4, поэтому ее значение dist изменяется, а вершина 4 получила сообщение, что значение dist вершины 3 изменилось, поэтому значение dist вершины 4 так же изменяется:

min_dist_df = pregel_min_dist(edges_df, min_dist_df, 1)
min_dist_df.show()

Выполним еще один шаг (superstep) - вершина 5 получила новое сообщение от вершины 4, поэтому значение dist вершины 5 было уточнено:

min_dist_df = pregel_min_dist(edges_df, min_dist_df, 1)
min_dist_df.show()

Выполним еще один шаг (superstep) - изменений больше нет, алгоритм сошёлся:

min_dist_df = pregel_min_dist(edges_df, min_dist_df, 1)
min_dist_df.show()

Замечания:

значения dist у вершин уточняются на каждом шаге, и в конечном итоге алгоритм сходится,
вершина 6 не связана с вершиной 1, поэтому минимальное расстояние равно бесконечности.

Топологическая сортировка (Topological Sort)

Топологическая сортировка (Wikipedia) позволяет отсортировать граф таким образом, что:

в начале списка будут находиться независимые вершины, на которые никто не ссылается
далее идут вершины, которые ссылаются на независимые вершины
далее вершины, которые ссылаются на вершины из предыдущего пункта и т.д.

В результате в каждой вершине будет храниться порядковый номер вершины.

Топологическая сортировка применима только, если в графе нет циклов.

Самый распространенный пример топологической сортировки - это компиляция программ: к моменту компиляции одного модуля, все модули, от которых он зависит, должны быть уже скомпилированы.

Императивный алгоритм

Основная идея в том, что текущая вершина должна иметь порядок на единицу больше, чем максимальная из вершин, которые ссылаются на нее:

class TopologicalSortPregelVertex(PregelVertex[int, Tuple[TopologicalSortPregelVertex, TopologicalSortPregelVertex], int]):

    def __init__(self, id: int):
        self.id = id
        self.value = 1

    def compute(self, messages: List[int]) -> None:
        max_incoming_order = max(messages)

        if self.value < max_incoming_order + 1:
            self.value = max_incoming_order + 1

            for _, target, weight in self.out_edges():
                self.send_message(target.id, self.value)

Комментарии к коду:

TopologicalSortPregelVertex наследует PregelVertex, где типовые параметры:
1. int - тип значения, поярковый номер вершины;
2. Tuple[TopologicalSortPregelVertex, TopologicalSortPregelVertex] - тип ребра в формате: (исходная вершина, конечная вершина);
3. int - тип сообщения, т.е. порядковый номер вершины.
изначально считается, что каждая вершина независима, поэтому ее порядок равен 1;
метод compute корректирует порядок текущей вершины:
1. на вход приходят сообщения, которые были отправлены текущей вершине. Сообщения содержат значение порядка вершин;
2. выполняется поиск максимального порядка среди входящих сообщений;
3. максимальное значение порядка сравнивается с текущим значением: текущее значение должно быть не меньше, чем максимальный порядок среди всех входящих вершин увеличенный на единицу;
4. если значение в текущей вершине было обновлено, то отправить соседям сообщение, состоящее из актуального порядка текущей вершины.
реализация остальных методов исключена, т.к. по большей части зависит от окружения.

Алгоритм на Apache Spark

Решение для Apache Spark строится на базе DataFrame API запроса. Для исключения дублирования кода, основной алгоритм вынесен в функцию pregel_topological_sort (подробные комментарии ниже):

def pregel_topological_sort(edges: DataFrame, values: DataFrame, steps: int) -> DataFrame:
    result_df = values

    for i in range(1, steps + 1):
        result_df = (
            edges.where("src != dst")
                .join(result_df, col("src") == col("id"))
                .select(col("dst").alias("id"), col("ord").alias("message"))
                .groupBy(col("id")).agg(F.max("message").alias("message"))
                .join(result_df, "id", "right")
                .select("id", F.greatest(F.expr("message + 1"), "ord").alias("ord"))
        )
        if i % 5 == 0:
            result_df = result_df.checkpoint()

    return result_df

Комментарии к коду:

на вход приходит 3 параметра:
1. edges - датафрейм с рёбрами графа. В датафрейме обязательно должны быть колонки:
  - src - исходная вершина,
  - dst - конечная вершина.
2. values - датафрейм с вершинами графа. В датафрейме обязательно должны быть колонки:
  - id - идентификатор вершины,
  - ord - порядковое значение вершины в графе.
3. steps - количество шагов (superstep), которое необходимо выполнить, чтобы алгоритм сошёлся.
каждые пять шагов драйвер будет запускать план на исполнение.

Рассмотрим запрос поближе и укажем на аналогии с кодом на Python для вычисления связных компонент:

edges.where("src != dst") - исключить ребра, когда вершина ссылается на саму себя. Изначально ожидается, что в графе нет циклов, это лишь дополнительная защита;
edges.join(result_df, col("src") == col("id")) позволяет соединить датафреймы ребер и вершин, так в результате появятся как минимум четыре колонки:
1. src - исходная вершина;
2. dst - конечная вершина;
3. id - идентификатор вершины (равен src);
4. ord - текущее значение вершины (src и id). Это значение нужно отправить всем вершинам dst.
.select(col("dst").alias("id"), col("ord").alias("message")) формирует сообщение для каждой вершины. Фактически программа говорит, что сообщением является значение ord;
На рисунке ниже можно найти соответствие этой инструкции коду для вычисления связных компонент на Pregel:

.groupby(col("id")).agg(F.max("message").alias("message")) позволяет вычислить итоговое сообщение. Вершина dst может получить много сообщений от разных src вершин, а значит необходимо выбрать из сообщений максимальное значение;

.join(result_df, "id", "right") позволяет соединить итоговые сообщения с датафреймом, в котором находятся текущие значения. Как минимум в итоге получится три колонки:
1. id - идентификатор текущей вершины,
2. ord - текущее значение вершины,
3. message - итоговое сообщение от всех соседей. Нужно проверить больше ли значение ord текущей вершины, чем входящее сообщение увеличенное на единицу.
.select("id", F.greatest(F.expr("message + 1"), "ord").alias("ord")) позволяет вычислить итоговое значение:
1. id - текущая вершина,
2. F.expr("message + 1") - входящее сообщение увеличенное на единицу,
3. F.greatest(F.expr("message + 1"), "ord").alias("ord")) - выбрать максимум между сообщением, увеличенным на единицу, и текущим значением,
4. .alias("ord") - заменить текущее значение ord в вершине id на вычисленное.

result_df = (...) позволяет актуализировать значения вершин. Эта операция аналогична рассылке сообщений, но со всех вершин и сразу всем.

Пример работы

Приведенный граф тот же самый, который использовался в алгоритме поиска связных компонент.

Подготовка данных

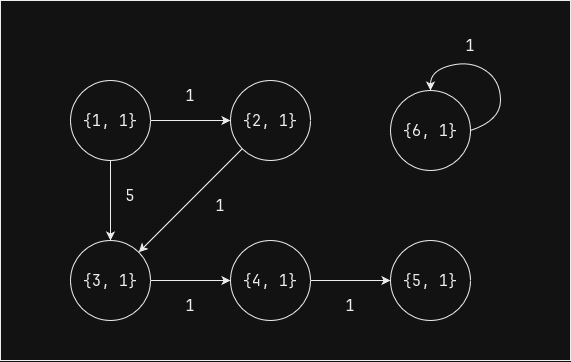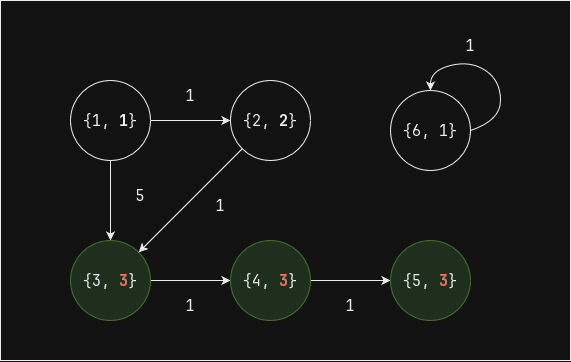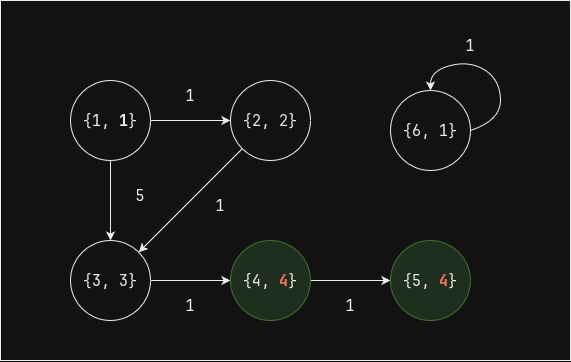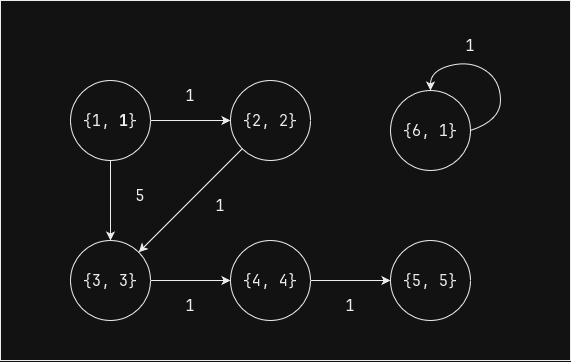
Каждая вершина изначально считается независимой, поэтому у них у всех порядковый номер 1 (колонка ord).

edges_df, vertices_df = small_graph()
sorted_df = vertices_df.withColumn("ord", F.lit(1))

Проследим как меняются значения в вершинах:

Начальное состояние - значение ord всех вершин равно 1:

sorted_df.orderBy("id").show()

Выполним один шаг (superstep) - все вершины за исключением 1 и 6 имеют входящие ребра, поэтому для них значение ord становится равным 2:

sorted_df = pregel_topological_sort(edges_df, sorted_df, 1)
sorted_df.orderBy("ord").show()

Выполним еще один шаг (superstep) - вершина 3 связна с вершиной 2, поэтому ее значение меняется на 3, т.к ее текущее значение равно 2. Вершины 4 и 5 увеличивают на единицу значение ord, т.к. вершина 3 передает вершине 4 значение 2, и вершина 5 получает от вершины 4 значение 2:

sorted_df = pregel_topological_sort(edges_df, sorted_df, 1)
sorted_df.orderBy("ord").show()

Выполним еще один шаг (superstep) - вершины 1, 2, 3 и 6 больше не получают сообщений, которые были бы больше чем их текущее значение, а вершина 4 получает от вершины 2 значение 3, и вершина 5 так же получает от вершины 4 значение 3, поэтому их значение становится равным 4:

sorted_df = pregel_topological_sort(edges_df, sorted_df, 1)
sorted_df.orderBy("ord").show()

Выполним еще один шаг (superstep) - только вершина 5 увеличивает свое значение ord на единицу, т.к.вершина 4 передала ей значение 4:

sorted_df = pregel_topological_sort(edges_df, sorted_df, 1)
sorted_df.orderBy("ord").show()

Выполним еще один шаг (superstep) - изменений больше нет, алгоритм сошёлся:

sorted_df = pregel_topological_sort(edges_df, sorted_df, 1)
sorted_df.orderBy("ord").show()

Замечания:

значения ord у вершин уточняются на каждом шаге, и в конечном итоге алгоритм сходится,
алгоритм назначает вершинам их порядковый номер, а реальная сортировка выполняется при помощи orderBy("ord").

Обобщение алгоритма

Может показаться сложным писать код для каждого случая, но если взглянуть на реализации, то можно найти закономерности.

Поставив все три реализованных алгоритма друг напротив друга, можно выделить закономерности и найти "подвижные части":

Основные отличия:

на второй строке вычисляется сообщение;
на третьей строке выполняется агрегация сообщений;
на последней строке выполняется вычисление нового значения вершины.

Дополнительно можно заметить, что для топологической сортировки еще накладывается условие, которое исключает тривиальные циклы (вершина ссылается на саму себя). Датафрейм edges передается в качестве параметра, и поэтому программист может предварительно наложить это условие на датафрейм перед передачей его в функцию.

Учитывая найденные отличия, можно реализовать обобщенную функцию (подробные комментарии ниже), которая будет вычислять любой алгоритм на графах с помощью Pregel:

def pregel_superstep(
    edges: DataFrame,
    values: DataFrame,
    message: Column,
    combiner: Callable[[Column], Column],
    computer: Column,
    **columns: Column
) -> DataFrame:
    message_box_df = (
        edges.where(col("src") != col("dst"))
            .join(values, col("src") == col("id"))
            .select(col("dst").alias("id"), message.alias("message"))
    )
    accumulator_df = (
        message_box_df
            .groupby(col("id"))
            .agg(combiner(col("message")).alias("message"))
    )
    result_df = (
        accumulator_df
            .join(values, "id", "right")
            .select("id", computer.alias("value"), *columns.values())
    )
    return result_df

Комментарии к коду:

Функция pregel_superstep принимает на вход шесть параметров:
1. edges - датафрейм с ребрами графа,
2. values - датафрейм с вершинами графа и начальными значениями,
3. message - объект типа Column выбирает из датафрейма колонку или выражение, которое является присланным сообщением,
4. combiner - лямбда функция (Column -> Column), которая агрегирует все входящие сообщения,
5. computer - объект типа Column выбирает из датафрейма колонку или выражение, которое будет итоговым значением вершины
6. columns дополнительный набор колонок, которые программист хочет видеть в итоговом датафрейме
тело функции разбито на части для упрощения восприятия. Составные части:
- message_box_df - почтовый ящик,
- accumulator_df - агрегация сообщений,
- result_df - датафрейм с вершинами и итоговыми результатами.

Связные компоненты

При помощи функции pregel_superstep можно реализовать алгоритм поиска связных компонент:

edges_df, vertices_df = small_graph()
cc_df = vertices_df.withColumn("value", col("id"))

for _ in range(5):
    cc_df = pregel_superstep(
        edges=bidirectional(edges_df),
        values=cc_df,
        message=col("value"),
        combiner=F.min,
        computer=F.least(col("value"), col("message"))
    )

cc_df.show()

+---+-----+
| id|value|
+---+-----+
|  1|    1|
|  3|    1|
|  2|    1|
|  4|    1|
|  6|    6|
|  5|    1|
+---+-----+

Примечание: функция bidirectional добавляет в датафрейм с ребрами ребра в обратном направлении.

Кратчайшее расстояние

При помощи функции pregel_superstep можно реализовать алгоритм поиска кратчайшего расстояния:

edges_df, vertices_df = small_graph()
pregel_min_dist_df = get_min_dist_init_df(vertices_df, start=1) \
    .withColumnRenamed("dist", "value")

for _ in range(5):
    pregel_min_dist_df = pregel_superstep(
        edges=edges_df,
        values=pregel_min_dist_df,
        message=F.expr("value + weight"),
        combiner=F.min,
        computer=F.least("message", "value")
    )

pregel_min_dist_df.show()

+---+-------------------+
| id|              value|
+---+-------------------+
|  1|                  0|
|  3|                  2|
|  2|                  1|
|  4|                  3|
|  6|4611686018427387903|
|  5|                  4|
+---+-------------------+

Топологическая сортировка

При помощи функции pregel_superstep можно реализовать алгоритм топологической сортировки:

edges_df, vertices_df = small_graph()
pregel_sort_df = vertices_df.withColumn("value", F.lit(1))

for _ in range(5):
    pregel_sort_df = pregel_superstep(
        edges=edges_df.where("src < dst"),
        values=pregel_sort_df,
        message=col("value"),
        combiner=F.max,
        computer=F.greatest(F.expr("message + 1"), "value")
    )

pregel_sort_df.orderBy("value").show()

+---+-----+
| id|value|
+---+-----+
|  1|    1|
|  6|    1|
|  2|    2|
|  3|    3|
|  4|    4|
|  5|    5|
+---+-----+

PageRank

Алгоритм PageRank (Wikipedia) позволяет определить на сколько авторитетен источник на основе источников, которые ссылаются на него. Изначально был создан Google для ранжирования страниц при поиске информации в интернете.

Алгоритм PageRank активно работает с исходящей степенью вершины, поэтому необходимо вычислить значение степени для каждой вершины:

out_deg = (
    edges_df
        .groupBy("src")
        .agg(F.count("src").alias("out_deg"))
        .withColumnRenamed("src", "id")
)

В формуле PageRank значение out_deg находится в знаменателе, а поэтому необходимо избавиться от нулей и пустых значений:

deg_vert_df = (
    vertices_df
        .join(out_deg, "id", "left")
        .select(
            "id",
            F.coalesce("out_deg", F.lit(1)).alias("out_deg")
        )
)

Изначально все вершины равны между собой, поэтому для всех устанавливается начальное значение равное 1:

page_rank_result_df = deg_vert_df.withColumn("value", F.lit(1))

Алгоритм PageRank никогда не сойдется к какому-то конкретному значению, поэтому очень часто его прерывают после определенного числа шагов, для примера используется 10 шагов:

for i in range(10):
    page_rank_result_df = pregel_superstep(
        edges=edges_df,
        values=page_rank_result_df,
        message=col("value"),
        combiner=F.sum,
        computer=F.expr("(0.15 + 0.85 * nvl(message, value)) / out_deg"),
        out_deg=col("out_deg")
    )
    if i % 5 == 0:
        page_rank_result_df = page_rank_result_df.checkpoint()

page_rank_result_df.orderBy("id").show()

+---+--------+-------+
| id|   value|out_deg|
+---+--------+-------+
|  6|1.000000|      1|
|  5|0.626186|      1|
|  4|0.560219|      1|
|  3|0.482611|      1|
|  2|0.260871|      1|
|  1|0.130436|      2|
+---+--------+-------+

Результат очень похож на правду:

на вершину 1 никто не ссылается, поэтому у вершины 1 самое низкое значение;
на вершину 5 ссылаются все остальные вершины напрямую или через другие вершины, поэтому у вершины 5 самое высокое значение;
вершина 6 находится вне зоны доступа других вершин, поэтому ее значение осталось равным начальному.

GraphFrames

Фреймворк GraphFrames, который работает поверх Apache Spark реализует большое число стандартных алгоритмов на графах. Для реализации своих алгоритмов предлагается использовать Pregel API.

PageRank

Ниже приведена реализация алгоритма PageRank при помощи GraphFrames, которая требует от пользователя следующие значения:

строка 11: начальное значение, в нашей реализации параметр values уже ожидает датафрейм с установленным начальным значением;
строка 12: механизм обновления столбца rank, в нашей реализации это параметр computer;
строка 15: формирование сообщения, в нашей реализации это параметр message;
строка 17: агрегация сообщений, в нашей реализации это параметр combiner.

initialMsg = F.lit(1.0)
# afterMsgAgg = (0.15 + 0.85 * nvl(message, value)) / out_deg
afterMsgAgg = (F.lit(0.15) + F.lit(0.85) * F.coalesce(Pregel.msg(), col("rank"))) / col("outDegree")

ranks = (
    graph.pregel
        .setMaxIter(10)
        # withVertexColumn создает дополнительную колонку, в которой будет накапливаться результат: rank
        .withVertexColumn(
            "rank", # в этом столбце будет накапливаться PageRank
            initialMsg, # начальное значение столбца
            afterMsgAgg # механизм обновления столбца
        )
        # sendMsgToDst определяет как формируется сообщение, которое необходимо отправить каждому соседу (по направлению ребра)
        .sendMsgToDst(Pregel.src("rank"))
        # aggMsgs определяет как сообщения будут агрегироваться для конкретной вершины
        .aggMsgs(F.sum(Pregel.msg()))
)

ranks.run().orderBy("id").show()

+---+---------+-------------------+
| id|outDegree|               rank|
+---+---------+-------------------+
|  1|      2.0|0.13060196535694696|
|  2|      1.0| 0.2612039307138939|
|  3|      1.0| 0.4836117921416817|
|  4|      1.0| 0.5622235842833633|
|  5|      1.0| 0.6301971685667266|
|  6|      1.0|                1.0|
+---+---------+-------------------+

Полный рабочий пример можно найти в репозитории.

Приведенный пример показывает, что наша реализация была корректно обобщена.

Разбиение по вершинам

Нигде в реализациях не был указан способ разбиения графа на части. Можно предположить, что это связано с небольшим размером датафрейма с рёбрами. Но правда в том, что Apache Spark автоматически разбил множество вершин на непересекающиеся множества.

Чтобы проверить этот факт, можно воспользоваться функцией spark_partition_id, которая каждой строке поставит значение ее партиции. Для примера был сгенерирован большой граф (см. notebook).

edges_df_with_part = edges_df.withColumn("partition_id", F.spark_partition_id())

df = (
    edges_df_with_part.alias("t1")
        .join(edges_df_with_part.alias("t2"), "src")
        .where("t1.partition_id != t2.partition_id")
        .select("src", "t1.partition_id", "t2.partition_id")
)
df.show(5)

+------+------------+------------+
|   src|partition_id|partition_id|
+------+------------+------------+
|250010|           0|           1|
|250010|           1|           0|
|250011|           0|           1|
|250011|           0|           1|
|250011|           0|           1|
+------+------------+------------+

Можно увидеть, что вершина 250010 находится в нескольких партициях. Таким образом, можно заключить, что Apache Spark автоматически разбивает граф по вершинам (vertex-cut).

Заключение

Фреймворк Pregel продолжает славную традицию парадигмы map-reduce, которая так же была создана в Google. Фреймворк позволяет сегментировать графы на любое число частей, и он все равно будет работать.

Приведенная реализация алгоритма на Apache Spark полагается на тот факт, что функции, которые агрегируют входящие сообщения, являются ассоциативными: min(a, min(b, c)) == min(min(a, b), c), что позволяет Apache Spark вычислить промежуточные результаты параллельно, а потом собрать все промежуточные результаты для финальной агрегации. Если какой-то из алгоритмов не сможет предоставить ассоциативную функцию для агрегации сообщений, то его невозможно будет реализовать на Apache Spark указанным способом. К счастью, множество задач имеет больше, чем одно решение, а поэтому большинство стандартных алгоритмов на графах можно реализовать при помощи Pregel.

Написание алгоритмов для Pregel требует корректировки мышления: программисты с опытом map-reduce смогут быстро разрабатывать свои алгоритмы, остальным потребуется практика.

Дополнительно

Все указанные алгоритмы оформлены в виде Jupyter Notebook и доступны на GitHub для экспериментов как локально, так и в облаке. Запуск в облаке (бесплатно) возможен через:

Задания для самостоятельной работы

Заинтересованный читатель может реализовать следующие алгоритмы:

(простой) сумма всех вершин в графе: в каждой вершине должна находиться итоговая сумма,
(сложный) раскраска графа: в каждой вершине должен находиться цвет вершины. Вдохновение можно почерпнуть из реализации этого алгоритма в Apache Giraph.

Теги:

Хабы:

Обработка больших и очень больших графов: Pregel

DISCLAIMER

TLDR

Мотивация

Обзор фреймворка Pregel

Вершинно-центричная программная модель

Синхронная модель исполнения

Обмен сообщениями

Разбиение графа

Практическое применение

Программный Интерфейс Pregel

Задача "Связные компоненты" (Connected Components)

Императивный алгоритм

Алгоритм на Apache Spark

Пример работы

Замечания

Задача о кратчайшем расстоянии (Single Source Shortest Path)

Императивный алгоритм

Алгоритм на Apache Spark

Пример работы

Топологическая сортировка (Topological Sort)

Императивный алгоритм

Алгоритм на Apache Spark

Пример работы

Обобщение алгоритма

Связные компоненты

Кратчайшее расстояние

Топологическая сортировка

PageRank

GraphFrames

PageRank

Разбиение по вершинам

Заключение

Дополнительно

Задания для самостоятельной работы

Публикации

Истории

Работа

Ближайшие события