kenoma 29 мар в 10:11

Варим кашу из нечеткой логики и вариационных автоэнкодеров

Сложный

13 мин

2.9K

Алгоритмы*Машинное обучение*Искусственный интеллект

✏️ Технотекст 2023

Пока весь мир затаив дыхание следит за большими языковыми моделями и одни грезят о том, как подсадят всех на свои сервисы LLM, а другие прикидывают как заменить бездушными симулякрами если не зажравшихся айтишников, то хотя бы ~~женщин~~ штукатуров и бухгалтеров, обычным ML‑инженерам, по щиколотку в коричневой жиже машинного обучения, приходится решать приземлемые задачи чем бог послал.

Кадр из фильма «Танкер „Дербент"» для привлечения внимания к проблеме машинистов — Кадр из фильма «Танкер „Дербент“» для привлечения внимания к проблеме машинистов

Когда перед нашей командой появилась очередная интересная задача из разряда «сделайте из датасета картинок с исправными пружинами детектор неисправных амортизационных комплексов», а из подручных средств только бытовые видеокарты да джентльменский набор сеток yolo, пришлось искать способы, как упростить себе жизнь хотя бы с разметкой данных. Появилась идея использования элементов нечеткой логики в связке с вариационными энкодерами (VAE) для целого круга задач, связанных не только с разметкой.

Начнем с небольшого лирического вступления.

Когда то давным давно, когда вариационные автоэнкодеры только только вышли на сцену, это было потрясающе. Казалось, что наконец‑то нейронные сети смогут извлекать знание из данных, представляя их в виде параметризированных моделей, прямо как это делают в формулах физики\математики! Воображение рисовало возможности легким движением руки отращивать волосы нужной длины на фотографиях людей, извлекать из тензометрических данных температурные параметры, сжимать покерные руки в эффективные бакеты малой размерности и надирать всем зад, но...

Реальность оказалась щедрой на сложности и разочарования. Чистая VAE даже в продвинутой реализации $\beta$ -VAE выдает набор латентных признаков, интерпретация которых требует перебора в некоторой заранее неизвестной области определения и экспертного мнения для отслеживания правильности того, правильно ли шевелится на выходе то, что вы шевелите на входе.

Механизм, по задумке, должен выглядеть так: покрутил параметр - увидел, что у стульчик на картинке завращался в ответ? Отлично, параметр вращения! Изменил другой параметр - размер стульчика начал меняться? Шикарно, параметр размера. И так до посинения...

А если переобучил модель с нуля, то и разбор параметров начинай заново.

Вышеописанная процедура не является особой проблемой, если задача довольно простая и не требует познаний в предметной области, рабочее время бесплатное, а вычислительное время бесконечное.

Реальные же задачи, чем они дальше от привычных обывателю вещей, тем сильнее завязаны на экспертные знания (то бишь разметку). И этих знаний всегда мало. И всегда велико искушение саму нейросетевую модель выдрессировать работать с ними.

Так появились расширенные вариационные автоэнкодеры (Conditional Variational Autoencoder, CVAE), которые вместе с задачей реконструкции и сжатия признаков решают еще и задачу классификации.

Положа руку на сердце, стоит признать что CVAE с полносвязными слоями в качестве классификаторов уступают и простым классификаторам и чистым VAE. Просто потому, что классификаторам не надо решать задачи реконструкции, а VAE не нужно бороться на многообразии в латентном пространстве с конкурентами за топологию.

Так какие преимущества дает CVAE?

Если посмотреть на некоторые реализации CVAE, то, кажется, что использование CVAE только лишь усиливает углеродный след: вопросы интерпретации латентных признаков не решены, а точности классификатора и реконструктора хуже.

Размышляя над тем, как (и зачем) можно улучшить CVAE, и перепробовав кучу подходов в духе dbscan/нечеткой кластеризацией/градиентного бустинга над скрытым слоем, как-то само собой родилось понимание, что необходимо обучать VAE и выполнять кластеризацию в латентном пространстве одновременно в процессе обучения.

Оказалось, что этого можно добиться, если использовать для модуля классификации в CVAE штуку, которую мы обозвали нечетким слоем.

Какие возможности это дает и расскажем в этой статье.

Предполагаем, что читатель в достаточной мере знаком с теорией и практикой построения VAE\CVAE, поэтому некоторые детали просто опустим. Благо, на Хабре есть достаточно статей по теме, например тут замечательный цикл.

Нечеткий слой

Сам термин "нечеткий" нами используется довольно свободно, по факту вся идея основана на принципах работы характеристической функции. Эти функции описывают степень принадлежности некоего входного значения к определенному нечеткому множеству, выражая эту степень от 0 (не принадлежит) до 1 (принадлежит полностью). Разновидностей функций принадлежности существует огромное количество, на любой вкус и цвет.

Но зачем городить огород, если есть прекрасная классическая гауссиана, для одномерного случая имеющая вид

$\mu(x)=e^{-(\frac{x-a}{b})^2}.$

Параметры и в этой формуле отвечают за смещение центра гауссианы относительно нуля и ее ширину, варьируя их можно более аккуратно подогнать гауссиану под конкретное нечеткое множество.

Многомерные гауссианы, которые представляют больший практический интерес, можно записать в виде $\mu(x,A)=e^{-||[A.\tilde x]_{1\cdots m}||^2}$ где это размерность пространства, а это матрица переноса:

$A_{(m+1) \times (m+1)} = \left[ {\begin{array}{cccc} s_{1} & a_{12} & \cdots & a_{1m} & c_{1}\\ a_{21} & s_{2} & \cdots & a_{2m} & c_{2}\\ \vdots & \vdots & \ddots & \vdots & c_{3}\\ a_{m1} & a_{m2} & \cdots & s_{m} & c_{m}\\ 0 & 0 & \cdots & 0 & 1\\ \end{array} } \right],$

где $c_{1\cdots m}$ - это центроид гауссианы, $s_{1\cdots m}$ ее масштабирующие факторы, а $a_{1\cdots m, 1\cdots m}$ параметры расположения гауссианы вокруг центроида.

Вопросы некоторых ограничений на матрицу (например, подматрица, составленная из $s_{1\cdots m}$ и $a_{1\cdots m, 1\cdots m}$ должна быть положительно определенной), мы оставим на случай, если нарвемся на недружелюбно настроенных математиков. Пока что можно нагло заявить, что параметры этой матрицы, с помощью волшебства обратного распространения ошибки в любимом ML-фреймворке подгонят бугорок гауссианы под целевое скопление входных векторов.

*Тот самый бугорок на 2D плоскости, по третьей оси отложено выходное значение характеристической функции*

Связав характеристические функции с отдельными классами в разметке можно интерпретировать датасет уже как набор нечетких множеств. Совокупность функций принадлежности для таких классов образует нечеткий слой, питоновская реализация которого носит название FuzzyLayer.

Модуль FuzzyLayer в процессе обучения не только стремиться сгруппировать входные вектора под те функции принадлежности, которые они активируют, но и адаптировать форму и месторасположение многомерной гауссианы.

Вживляем нечеткость в VAE

Проведя умозрительный эксперимент, можно обнаружить, что использование нечеткого слоя FuzzyLayer в CVAE не сильно вмешивается в работу VAE - составляющей, ведь и в самом деле, какая разница, где ему размещать свои распределения в латентном пространстве. Главное, чтобы размерности хватило аллоцировать кластеры неконфликтующим образом. Иными словами, роль FuzzyLayer сводится к указанию VAE где следует размещать вектора средних для распределений признаков так, чтобы они максимально соответствовали своим нечетким множествам.

Наглядная иллюстрация как задумывался эффект от применения FuzzyLayer в связке с VAE

Для демонстрации применения FuzzyLayer будем препарировать многострадальный MNIST и попробуем на нем построить CVAE классификатор два в одном: цифры и признак наличия в начертании цифры замкнутого округлого контура. Т.е. цифры 0,6,8,9 (обзовем из цифрами с кружком) налево, а 1,2,3,4,5,7 (без кружка) направо.

Ради наглядности, размерность латентного вектора выберем равной двойке.

Код блокнота доступен на гитхабе, обратим внимание на ряд моментов.

Момент первый - кодирование меток

При предобработке датасетов целевые метки для классификации преобразуются в два вектора - вектор целевого значения выхода нечеткого слоя и маска.

Вектор маски это вектор той же размерности, что и целевой вектор, но на каждой позиции находится 0, если позиция не участвует в вычислении невязки и 1 - если участвует.

Маска, состоящая из одних нулей означает, что данный образец при обучении проходит только через VAE и не вносит никакого вклада в структуру нечеткого слоя.

Например, для цифры 0, полноценно участвующей в обучении CVAE, такое представление разметки под нашу задачу будет иметь вид:

	_{Цифра 0}	_{Цифра 1}	_{Цифра 2}	_{Цифра 3}	_{Цифра 4}	_{Цифра 5}	_{Цифра 6}	_{Цифра 7}	_{Цифра 8}	_{Цифра 9}	_{С кружком}	_{Без кружка}
_{Целевой}	1	0	0	0	0	0	0	0	0	0	1	0
_Маска	1	1	1	1	1	1	1	1	1	1	1	1

Все компоненты маски единичные, что означает, что все компоненты целевого вектора будут учтены при вычислении невязки.

Маска позволяет реализовать ряд нестандарных вещей, обретающих смысл в сеттинге, когда VAE - компонента нашей модели строит латентные представления входных векторов, а нечеткий слой над этим дополнительно выполняет кластеризацию в соответствии с предоставленной ему разметкой.

Во-первых, с помощью маски можно пополнять разметку только для отдельно взятых классов.

Для цифры 0 это будет выглядеть так:

	_{Цифра 0}	_{Цифра 1}	_{Цифра 2}	_{Цифра 3}	_{Цифра 4}	_{Цифра 5}	_{Цифра 6}	_{Цифра 7}	_{Цифра 8}	_{Цифра 9}	_{С кружком}	_{Без кружка}
_{Целевой}	1	0	0	0	0	0	0	0	0	0	1	0
_Маска	1	0	0	0	0	0	0	0	0	0	0	0

Обратите внимание, что признак С кружком мы тоже отключили. Этот прием полезен, когда по каким-то причинам есть необходимость сосредоточиться на отдельно взятом классе, а все остальное стоит проигноировать.

Во-вторых, бывали ли у вас ситуации, когда вы смотрите на результаты классификации кошек и вдруг видите что сетка сработала на что-то совершенно несуразное, и к кошкам отношение имеющее только общим нарративом?

Можете не отвечать!

В примере с цифрой 0 такая ситуация бы выглядела так:

	_{Цифра 0}	_{Цифра 1}	_{Цифра 2}	_{Цифра 3}	_{Цифра 4}	_{Цифра 5}	_{Цифра 6}	_{Цифра 7}	_{Цифра 8}	_{Цифра 9}	_{С кружком}	_{Без кружка}
_{Целевой}	0	0	0	0	0	0	0	0	0	0	1	0
_Маска	1	0	0	0	0	0	0	0	0	0	0	0

С помощью маски мы обозначили, что разметка относится только к классу Цифра 0, а в целевом векторе указали, что представленный пример точно не является цифрой 0. Чем же является этот пример на самом деле, мы не знаем и нет времени выяснять, пусть нейронная сеть сама разбирается.

Такие манипуляции с масками позволяют целенаправленно влиять на отдельно взятые функции принадлежности нечеткого слоя, не задевая остальные. При этом VAE в составе модели продолжает обучаться безотносительно того, подаем ли мы пример с разметкой или без.

Момент второй - функция потерь

Особых ухищрений с невязками при обучении не производим, просто суммируем их

    loss = loss_recon + loss_kl + gamma * loss_fuzzy

Первые два слагаемые знакомы тем, кто имел дело с VAE, а третий компонент это среднее суммы квадратов невязки целевого вектора с выходом нечеткого слоя, пропущенная через маску:

target_firings = ... #целевой вектор
mask = ... #маска разметки
loss_fuzzy = (mask * torch.square(target_firings - predicted_labels)).sum(-1).mean()

Когда дело доходит до частично размеченных датасетов, возможны ситуации, что вклад от loss_fuzzy перебивается другими компонентами невязки. В этом случае можно увеличить значение параметра gamma, чтобы усилить его.

Если же размеченных данных совсем мало, в качестве крайней меры есть вариант делать два отдельных прохода обратным распространением ошибки за итерацию - сначала лоссом от чистого VAE, а затем от того, что есть в loss_fuzzy.

Иногда помогает.

Момент третий - модель

Структура сети для нашего демонстрационного проекта выбрана наобум - энкодер и декодер на свертках с парочкой полносвязных слоев.

Внимательный и опытный взгляд моментально обнаружит, что в структуре энкодера и декодера нет вообще никаких отличий от VAE, поэтому их код приводить тут не будем, посмотрите в блокноте сами, распишем тут ряд ньюансов, которые вы там встретите.

Структура CVAE с нечетким слоем FuzzyLayer

Интерес представляет класс CVAE, в котором объединены компоненты энкодера, декодера и FuzzyLayer в качестве классификатора:

class CVAE(nn.Module):
    """
    Реализация Conditional Variational Autoencoder (C-VAE) 
    
    Args:
        latent_dim (int): Размер латентного вектора.
        labels_count (int): Количество выходов классификатора
    """
    def __init__(self, latent_dim, labels_count):
        super(CVAE, self).__init__()

        self.encoder = Encoder(latent_dim)        
        self.decoder = Decoder(latent_dim)

        self.fuzzy = nn.Sequential(
             FuzzyLayer.fromdimentions(latent_dim, labels_count, trainable=True)
        )
        
    def forward(self, x):
        """
        Возвращает компоненты внутренних слоев CVAE, результаты реконструкции и классификации
        
        Args:
            x (torch.Tensor): Входной вектор.
        
        Returns:
            mu, x_recon, labels
        """

        mu, _,  _, = self.encoder(x)
        x_recon = self.decoder(mu)
        labels = self.fuzzy(mu)

        return mu, x_recon, labels
    
    def half_pass(self, x):
        """
        Возвращает вывод только энкодера и классификатора, без операции декодирования
        """
        mu, logvar, z = self.encoder(x)
        labels = self.fuzzy(mu)

        return mu, logvar, z, labels
    
    def decoder_pass(self, latent_x):
        """
        Реконструирует вывод из вектора latent_x
        """
        return self.decoder(latent_)

Из общих особенностей модели стоит отметить, что используется функция активации SiLU вместо распространенной Relu. В последнее время появляется все больше свидетельств о том, что нейронные сети с SiLU ведут себя лучше в процессе обучения в плане стабильности и сходимости, поэтому не будем отставать от модных тенденций.

Другой особенностью нашей модели вариационного автоэнкодера является наличие постоянного небольшого слагаемого eps к компоненту дисперсии в энкодере. Этот прием был подсмотрен из других реализаций автоэнкодеров и в целом повышает стабильность обучения.

Следующий аспект модели, на который стоит обратить внимание - нормализация батчей. Как показывает практика, без батчнорма у автоэнкодеров есть тенденция не разворачивать латентное пространство в кластерную структуру. Судя по всему, это довольно распространенная проблема автоэнкодеров и нормализация батчей позволяет с этим в какой то мере бороться.

В ходе обучения представленной модели применяется градиентный клиппинг для того, чтобы немного замедлить скорость сходимости весов сетки в надежде на более качественные итоговые результаты.

И последнее, что стоит сказать про представленную модель это то, что она не является по факту системой нечеткого вывода, поскольку одних характеристических функций недостаточно, чтобы ее так обозвать. Если присовокупить к FuzzyLayer линейный слой на входе и софтмакс на выходе, то в таком виде эту конструкцию уже можно выдать за нечеткий вывод Мамдани. Тогда латентный вектор от VAE будет представлять собой набор признаков, линейная комбинация которых активирует то или иное правило нечеткого вывода.

Сейчас так глубоко погружаться в это не будем, просто отметим что есть возможность построения и таких систем.

Как говорится, рычаг я дам, а камень я не дам.

Эксперименты с полностью размеченным датасетом

Перейдем наконец к картинкам и графикам.

Первым делом рассмотрим чистый VAE с отключенными нечеткими компонентами (gamma = 0), чтобы у нас появились хоть какие-то ориентиры. После 50 итераций обучения на тестовой выборке имеем следующую картину для потерь VAE - составляющей:

Графики функций потерь для обычного VAE, слева направо - полный лосс, лосс реконструкции и KL-лосс.

А в латентном пространстве образовались какие-то структуры, которые раскрашены по фактической метке класса

Латентное пространство чистого VAE, раскрашенное по меткам цифр

Кластеры довольно хорошо соотносятся с реальными цифрами, хотя и видны наползания и наложения друг на дружку.

На этом моменте нужно побороть сильное желание выполнить поиск кластеров с помощью того же k-means и жить дальше в проклятом мире, который сами же и создадим.

Идем дальше, теперь включим нечеткий слой (gamma = 1) и обучим модель на полностью размеченном датасете 10 классов цифр, а 2 класса очертаний пока отключим через маску.

Графики функций потерь для обычного VAE, слева направо - полный лосс, лосс реконструкции и KL-лосс. Голубым цветом обозначены значения функций потерь для CVAE с нечетким слоем.

По итоговым потерям VAE-компоненты принципиальной разницы нет, общий лосс разве что выше из-за того, что к нему прибавился loss_fuzzy.

Точность классификации 10 цифр на тестовой выборке составила по итогу ~ 96.52%. Прежде чем вы с хохотом закроете эту статью, вспомните, что размерность латентного пространства равна двойке. В практически полезных задачах борьбу за точность вывода стоит начинать с подбора правильной размерности латентного вектора. В задаче MNIST нам удалось получить результаты выше 99% на размерностях латентного пространства выше 12. Однако визуализация 12-мерных пространств это дело на любителя и, нет, t-sne плохая рекомендация, потому что мы и так знаем, что у нас имеются ярко выраженные кластерные группировки.

Вот так выглядит структура латентного пространства с уже включенным лоссом для нечеткого слоя

Структуры в латентном пространстве СVAE с нечетким слоем, раскрашенные по соответствующим им цифрам

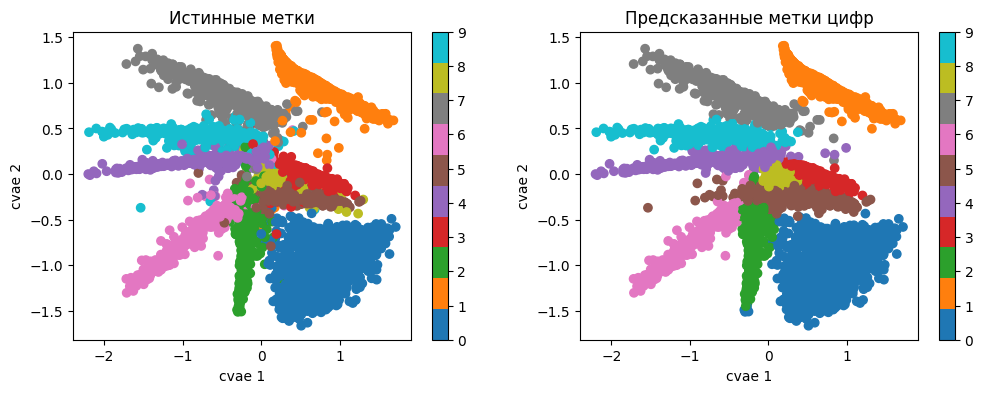
Кластеры стали заметно лучше разделены, изменилось их взаимное расположение.

Включим все 12 классов, к 10 цифрам добавим еще два очертательных класса и посмотрим что будет.

Графики функций потерь для обычного VAE, слева направо - полный лосс, лосс реконструкции и KL-лосс. Розовым цветом обозначены значеня функций потерь для 12 классового CVAE с нечетким слоем.

Лоссы VAE-составляющей плюс-минус те же, но точность классификации 10 цифр на тестовой выборке составила уже ~ 97.52%, на целый процент выше. Доказывать статистически и разбираться с этим явлением сейчас не будем, не об этом статья. Но забегая вперед, отметим, что CVAE с нечетким классификатором действительно работает тем лучше, чем больше разнообразной непротиворечивой экспертной информации об элементах обучающей выборки мы предоставляем.

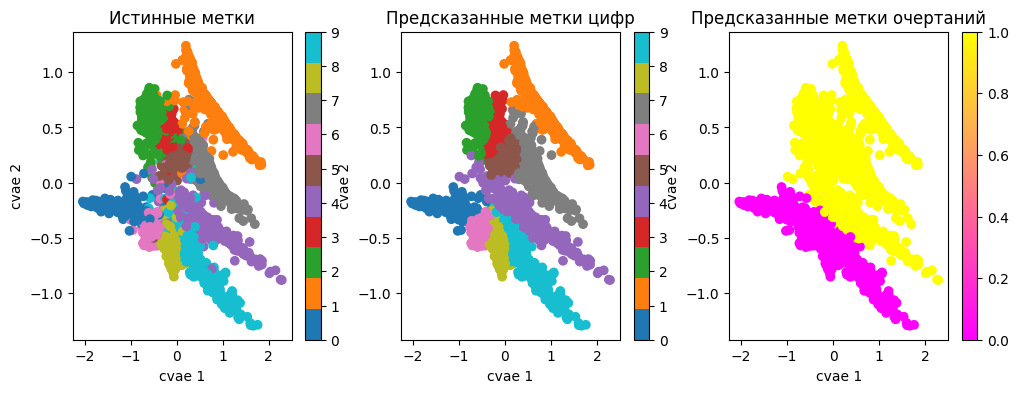
Из структур латентного пространства можно вывести ряд интересных наблюдений.

Прежде всего это класс цифры 4, который оказался пограничным между классами с замкнутыми округлыми очертаниями и без. Оказывается, некоторые цифры 4 имеют варианты начертаний с замкнутой верхушкой. При этом наибольшая область соприкосновения с 4 есть у класса 9 и 0, а классы 6 и 8 с четверкой практически не соприкасаются.

Попробуем осмысленно попутешествовать теперь по латентному пространству и превратим 9 в 4 двумя разными способами - первый заходящий недалеко в область четверок с замкнутыми контурами, а второй - подальше от линии соприкосновения в глубь глубже в кластер 4.

Маршруты путешествия по латентному пространству. Маршрут 1- близко линии разделения, ожидаем увидеть замкнутые четверки. Маршут 2 - дальше от линии разделения, ожидаем четверки без замкнутого сверху контура.

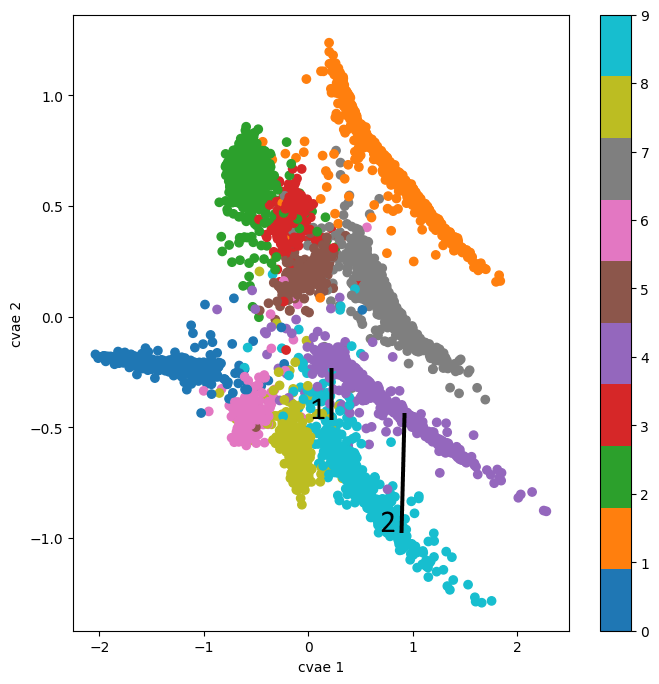
Цифры, сгенерированные по маршруту 1 получились более размытыми и трудно различимыми друг от друга, а контуры у четверок - замкнутыми сверху.

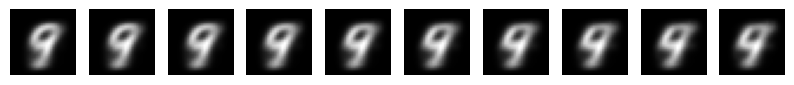
На втором маршруте изображения получились более четкими и проще различимыми друг от друга, а контуры четверок - разомкнутыми.

Принципиальный момент тут заключается в том, что мы только что получили инструмент, с помощью которого можно целенаправленно трансформировать и генерировать данные, с которыми работает CVAE. При этом есть возможность наделить их свойствами, переданными с помощью экспертного знания в разметке. Напоминаем, что конкретные параметры центроидов кластеров и области их размещения можно вытащить из матрицы соответствующих термов нечеткого слоя.

Частично размеченные датасеты и ускоренная доразметка

Перейдем ко второй коронной фишке нечетких CVAE - обучению на частично размеченных датасетах.

Приведем зависимость точности 10 циферного классификатора на тестовом датасете от процента неразмеченных данных.

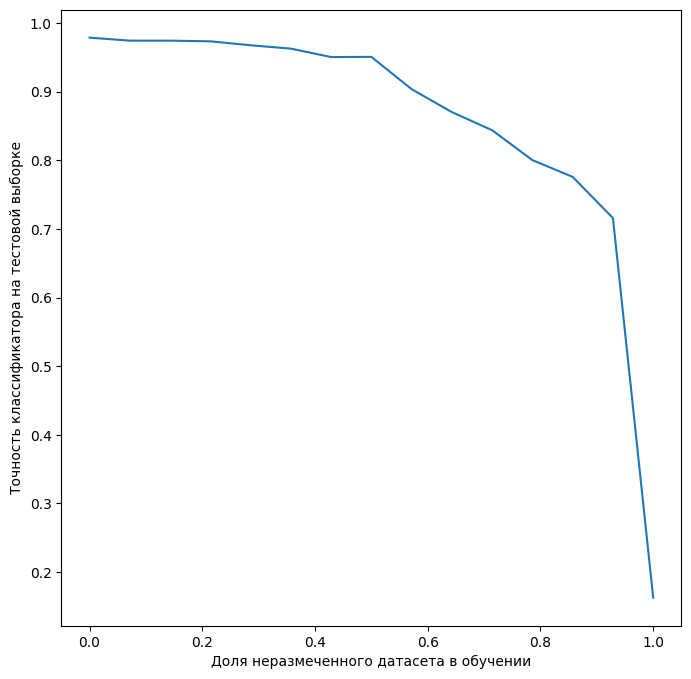
Да, с точки зрения статистики результат не вполне корректный, однако принципиальный момент тут отражен, и его не скроешь за ложью статистики: более менее приемлемых результатов можно добиться и на половине размеченного датасета, однако дальнейшее сколько-нибудь значимое улучшение возможно если докинуть еще столько же размеченных данных. Эффект этот связан прежде всего с тем, что при разметке квадратно-гнездовым способом, когда размечается все, что под руку попадает, нередка ситуация избыточной разметки. Другими словами, в таких случаях разметка новых примеров не дает нового знания нейросетевой модели.

Нами применяется подход, когда CVAE с нечеткими слоями обучался на небольшой порции размеченных данных, а дальнейшая разметка осуществляется итеративно, с помощью подсказок от CVAE. В каждом цикле разметки отмечаются новые примеры классов и ошибки, сделанные на предыдущей итерации. После доразметки новой небольшой порции данных CVAE дообучается и процедура повторяется заново. Процесс разметки прекращается, когда новая порция данных не дает существенного прироста в качестве вывода модели. Затем принимается решение или построить более сложную CVAE или эксплуатировать получившуюся модель.

Приведенная процедура оказалась очень эффективной для быстрого прототипирования моделей в одну каску и в сжатые сроки.

Возможная причина такой эффективности скорее всего связана с тем, что в процедуре дообучения не требуется кардинальной перестройки многообразия латентного представления данных - фичи VAE и так уже примерно расположены на своих местах, центроиды гауссиан из нечеткого слоя слегка мигрируют на новые позиции при дообучении, все ровно, плавно, без надрывов.

Заключение

На текущий момент это все, чем мы хотели бы поделиться с вами. Из больших вопросов, которые не были рассмотрены, осталась детекция аномалий, которая с помощью FuzzyLayer становится интересным и увлекательным делом.

Расскажем об этом в следующий раз, если захотите.

В сухом остатке, представлена модель CVAE с нечетким классификатором, которая позволяет реорганизовать структуру латентного пространства максимально щадящим для VAE образом, сохраняя ее кластерную структуру. Это дает возможность с помощью экспертного знания (разметки) локализовать области латентного пространства, связанные с конкретными классами из разметки. А это в свою очередь делает процесс генерации из латентных векторов более управляемым процессом.

С другой стороны, при дообучении таких моделей отсутствие взрывного перестроения латентного многообразия делает возможным продедуру итеративной разметки минимально необходимого датасета для приемлемого решения задачи.

За помощь в данной публикации спасибо @dnlhov, вместе с которым мы эту тему развиваем до продуктового состояния. Также выражаю благодарность @sukharudzeи @St_Hedgehogза продуктивные обсуждения и замечания.

Полный код модулей и примеров, упоминаемых в статье можно найти в репозитории pytorch-fuzzy.

Теги:

Хабы:

Варим кашу из нечеткой логики и вариационных автоэнкодеров

Публикации

Истории

Работа

Ближайшие события