Коротенькое ТЗ: создадим игру, в которой можно будет привычными способами (что-то вроде стандартного FPS контроллера) управлять перемещением игрок�� по поверхности ленты Мебиуса.
Игру в 3D с управлением от первого или третьего лица можно создать на любом современном движке минимальными усилиями — на все ключевые компоненты есть готовые решения, остается их только подключить. В чем сложность использования готовых компонентов на ленте Мёбиуса? Если коротко, сложность в гравитационном поле.
Более развернуто:
Мир большинства игр (конечно, мы рассматриваем игры с бегающим героем в 3D) — плоскоземельный мир с однородным гравитационным полем. Вектор силы земного притяжения не нуждается в серьезных расчетах. Взяли орт «минус Up» (по более-менее традиционным соглашениям о системах координат это {0; -1; 0}), умножили его на mg, готово. Гравитация в окрестностях ленты нуждается в более сложной модели.
Прямое следствие плоскоземельности — возможность упростить 3D пространство. Вектор гравитации — это еще и вектор вертикали, задающий ось «курсового» вращения контроллера игрока (мышь влево-вправо). Очень удобно иметь эту ось постоянной, занимаясь лишь двумя углами Эйлера из трех. В нашем случае очевидно, что ось будет подвижной.
Как вообще должно работать гравитационное поле на ленте Мёбиуса, чтобы по ней можно было ходить? Здесь возможны некоторые вариации, но более-менее логичным выглядит правило: направление местного результирующего вектора притяжения ленты не должно слишком отличаться от нормали к поверхности ленты в ее ближайшей точке. Это правило должно соблюдаться для тех участков, в которых мы собираемся обеспечивать привычную ходьбу.
Вооружившись этим замыслом, перейдем к математическому описанию мира.
Генерируем террейн
Примем, что линия, разрезающая ленту Мёбиуса (далее - «лента») вдоль посередине, представляет собой окружность с центром в начале координат (далее — «большая окружность»). Она будет лежать в плоскости Oxy.
Будем собирать ленту из тонких «брусков», нанизываемых своими серединами на большую окружность. Расположим каждый из них вдоль оси Oz. Получаем сформированную из брусков цилиндрическую поверхность. Для получения ленты осталось закрутить ее.
Каждый брусок получит индивидуальный поворот. Все они поворачиваются вокруг «своих» касательных к большой окружности, значение угла поворота определяется угловым положением бруска на ней, отсчитанным вдоль её дуги.
using System.Collections; using System.Collections.Generic; using UnityEngine; public class Root : MonoBehaviour { private const int NUM_OF_ITEMS = 1250; [SerializeField] private GameObject terrainItem; private GameObject InstantiateItem(float posRadians) { Vector3 pos = new Vector3(Mathf.Cos(posRadians), Mathf.Sin(posRadians), 0f); pos = pos * WorldPhysics.GetTerrainRadius(); GameObject res = Object.Instantiate(terrainItem, pos, Quaternion.identity); float degreesPos = RadToDeg(posRadians); res.transform.Rotate(new Vector3(Mathf.Cos(posRadians + Mathf.PI / 2f), Mathf.Sin(posRadians + Mathf.PI / 2f), 0f), degreesPos / 2f); return res; } private float RadToDeg(float radians) { return radians * 180f / Mathf.PI; } void Start() { float stepRadians = 2 * Mathf.PI / NUM_OF_ITEMS; for (int i = 0; i<NUM_OF_ITEMS; i++) InstantiateItem(i * stepRadians); } }
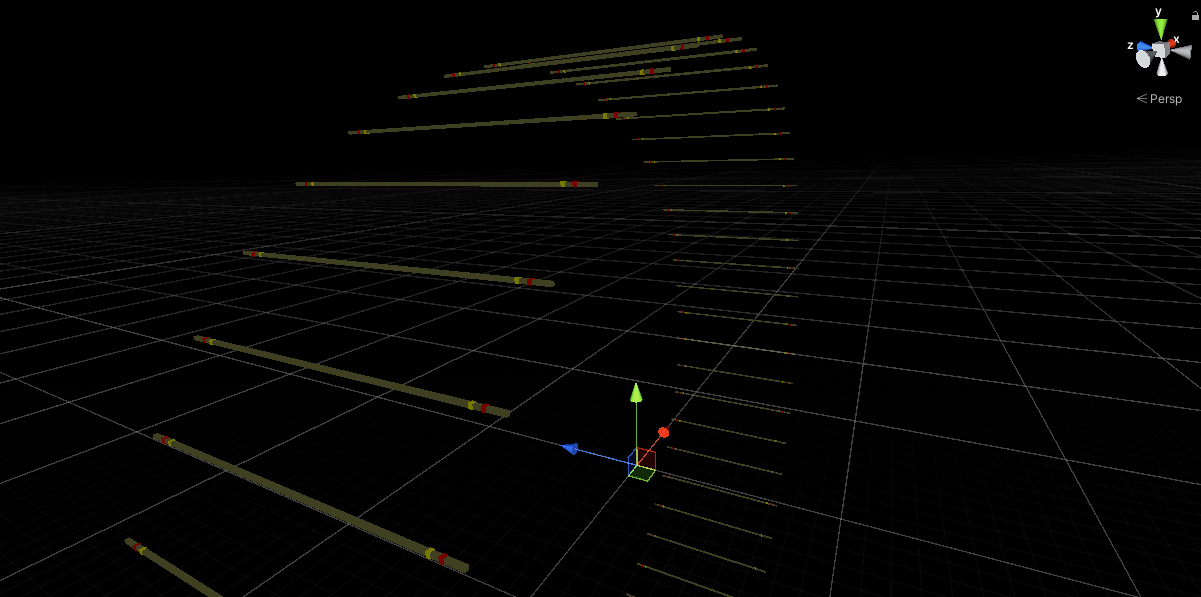
Продвигаясь вдоль большой окружности на угол 2π радиан, мы должны повернуть ленту на π радиан, следовательно, соотношение углов будет 1 к 2.

Продвижение по дуге большого круга с вызовами instantiateItem() реализовано в методе Start(). Передаваемое значение — угол дуги большой окружности, отсчитанный от оси Ox до позиции конкретного бруска. По этому значению в методе instantiateItem() будет определено, где установить новый брусок и как его повернуть.
Наименее очевидной частью скрипта выглядит вызов res.transform.Rotate() внутри метода instantiateItem(). Первым аргументом передается трехмерный вектор оси поворота (в нашем случае это касательная к большой окружности), вторым — величина поворота в градусах.
Очевидно, «плотность» ленты регулируется значением константы NUM_OF_ITEMS.
Приемлемый внешний вид — вещь субъективная, но за отправную точку можно принять, что при радиусе большой окружности 20 метров можно сделать почти сплошную ленту из примерно 1200 довольно тонких «брусков».
Создаем гравитационное поле
Было бы странно иметь привычную гравитацию и механику ходьбы после ухода с поверхности ленты в открытый космос. Определим для привычной физики пространство внутри тора, содержащего ленту. Радиус образующей его окружности равен половине ширины ленты, или, проще говоря, нам нужен минимальный «бублик», содержащий в себе ленту. За пределами этой фигуры гравитация будет принципиально другой, а движение перестанет быть управляемым.
При таком подходе на удалении от краев ленты (при ходьбе около центральной части «тропинки») все работает стандартно. По мере приближения к ним нарушается безопасность выполнения прыжков. Можно нечаянно покинуть область действия гравитации ленты и улететь.
Такое свойство ленты кажется естественным. Вполне вероятно, что аналогичный риск присутствует и на настоящих космических лентах для ходьбы.
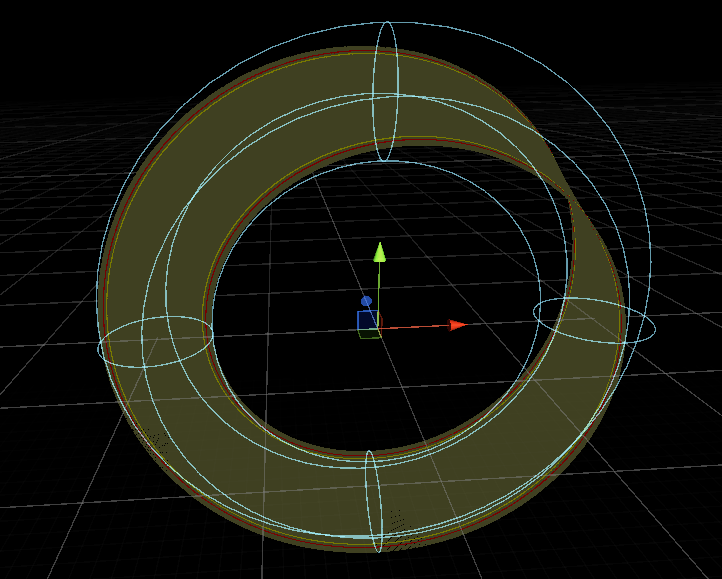
Выше сказано, что желательным направлением гравитации является нормаль к поверхности ленты возле игрока.
Существует довольно много вариантов реализации расчета поля:
Хранить данные — предварительно просчитанные значения вектора гравитации, в трехмерном массиве, где его индексы массива соответствуют движению вдоль трех осей. Зная текущую позицию, можно было бы взять значения из ближайшей соответствующей ячейки или из нескольких ячеек с последующей интерполяцией.
Вычислять гравитацию по закону всемирного тяготения, приняв какое-то огромное значение плотности вещества для ленты, и разбив ее на небольшие притягивающие элементы. Вектор гравитации будет суммой притяжений всех элементов. Отметим, что при точном расчете правило действия гравитации по нормали выполняться не будет.
Можно считать вектор ближайшей нормали при каждом обращении во время выполнения.
Приведенный список не может претендовать на полноту, а сравнение достоинств разных методов с учетом их возможных модификаций и оптимизаций займет не одну статью. Ограничимся отражением факта, что для реализации был выбран третий путь.
Логика приложения внешних сил помещена в статический класс WorldPhysics. Рассмотрим методы формирования гравитации.
static public bool IsInOuterSpace(Vector3 position) { Vector3 projOnWorldPlane = position; projOnWorldPlane.z = 0f; projOnWorldPlane = projOnWorldPlane.normalized; Vector3 grndOrig = projOnWorldPlane * terrainRadius; return (position - grndOrig).sqrMagnitude > SQ_HALF_TER_WIDTH; }
Определим, находимся ли мы внутри тора, где действует «обычная механика» ходьбы. Параметр position (позиция объекта), учитывая наше соглашение о расположении ленты, является радиус-вектором из центра большой окружности. Легко найти ближайшую к position точку большой окружности (проекция вектора position на Oxy, нормализация полученного вектора и умножение результата на радиус большой окружности). Далее остается проверить дистанцию между position и найденной точкой. Она сравнивается с радиусом образующей окружности разграничивающего тора, равной половине ширины ленты. На практике для большей эффективности вычислений будем сравнивать квадраты величин (имеем право, поскольку операнды неотрицательные).
Научившись понимать, на ленте мы или в открытом космосе, приступим к вычислению местной вертикали «внутри бублика».
static public Vector3 GetLocalGravity(Vector3 position) { Vector3 projOnWorldPlane = position; projOnWorldPlane.z = 0f; projOnWorldPlane = projOnWorldPlane.normalized; float worldAngleCos = Vector3.Dot(new Vector3(1f, 0f, 0f), projOnWorldPlane); float worldAngle = Mathf.Acos(worldAngleCos); if (position.y < 0f) worldAngle = Mathf.PI * 2 - worldAngle; Vector3 grndRotationAxis = Vector3.Cross(WORLD_AXIS, projOnWorldPlane).normalized; Quaternion grndItemRot = Quaternion.AngleAxis(worldAngle * 90f / Mathf.PI, grndRotationAxis); Vector3 grndNormal = grndItemRot * projOnWorldPlane; Vector3 grndOrig = projOnWorldPlane * terrainRadius; Vector3 grndToPos = position - grndOrig; float posToGrndDist = Vector3.Dot(grndToPos, grndNormal); Vector3 gravityDirection = -posToGrndDist * grndNormal; return gravityDirection.normalized; }
Метод принимает позицию и возвращает единичный вектор направления местной вертикали.
Последовательность вычислений включает уже знакомую проекцию на плоскость большой окружности, вычисление угла позиции в ней, отсчитанного от оси Ox через скалярное произведение векторов, определение вектора местной касательной к большой окружности (он же ось вращения местного элемента террейна, см. описание создания ленты выше), вращение нормализованного вектора проекции вокруг местной оси крутки террейна на половину позиционного угла (то есть на угол крутки террейна). Местная касательная к большой окружности определяется через векторное произведение векторов: этот вектор перпендикулярен как WORLD_AXIS (ось Oz), так и нормализованной проекции радиуса-вектора на Oxy projOnWorldPlane (касательная к окружности перпендикулярна радиусу в точке касания и перпендикулярна нормали к плоскости окружности). Поворот вектора на заданный угол вокруг заданной оси выполняется с помощью класса кватернионов Unity, имя AngleAxis() точно отражает суть метода.
Теперь, имея позицию игрока, мы точно знаем, куда направлена сила тяжести. В коде проекта на GitHub есть также контроллер игрока с механикой ходьбы, бега, прыжков и полета в открытом космосе. Возможно, этим компонентам будут посвящены новые публикации.
