
«Наименьшее первоначальное отклонение от истины умножается впоследствии тысячекратно» (Аристотель)
«Смещение одного электрона на миллиардную долю сантиметра в какой-то момент может сыграть решающую роль в том, погибнет ли человек год спустя в лавине или спасётся» (Алан Тьюринг)
«Кто в себе не носит хаоса, тот никогда не породит звезды» (Фридрих Ницше)
«Эволюция – это хаос с обратной связью» (Джозеф Форд)
«Поистине творческие перемены и большие сдвиги происходят прямо на грани хаоса» (Роберт Билдер)
«Значительная идея организации не может быть получена в мире, в котором всё необходимо и нет ничего случайного» (Норберт Винер)
Являются ли случайность и хаос фундаментальными свойствами нашего мира, или за ними всегда скрывается некий порядок, а нам просто не хватает знаний и точности измерений, чтобы его постичь? Изучением этого вопроса занимаются несколько тесно связанных между собой междисциплинарных наук: синергетика, неравновесная термодинамика, теория хаоса, теория катастроф, фрактальная геометрия, теория систем и кибернетика. На первый взгляд эти дисциплины очень абстрактны и совершенно непонятны без изучения их сложного математического аппарата. Но в действительности они гораздо ближе к жизни, чем квантовая механика или теория относительности, поскольку имеют дело не со «сферическими конями в вакууме», а с реальными процессами.
О явлениях хаоса и самоорганизации я рекомендую прочитать книгу Джеймса Глейка «Хаос. Создание новой науки» (1987). Если же у вас нет ни времени, ни желания изучать всю историю науки о хаосе, вы узнаете всё самое важное из данной статьи. Здесь я разъясняю множество специфических терминов, которые приведут в ужас даже хорошо образованного человека: эмерджентность, синергия, флуктуации, диссипативные структуры, динамический хаос, точка бифуркации, аттракторы, фракталы и т.д. Также мы выясним, не противоречит ли самоорганизация второму началу термодинамики и действительно ли случайность, необратимость и неустойчивость являются источниками всякого развития. Это будет первая из серии статей, посвящённых теме эмерджентности, происхождения жизни и универсальной эволюции.
Синергетика и неравновесная термодинамика
Традиционно целью науки считается поиск закономерностей среди окружающего нас беспорядка и предсказание будущего по начальным условиям в прошлом или настоящем, которые можно измерить с необходимой для этого точностью. Ньютоновская механика выполняла большинство поставленных перед ней практических задач безотказно, и мир представлялся детерминированным часовым механизмом. Квантовая механика разрушила эту идиллию. Многие до сих пор верят, что в природе хаоса нет, всё идёт по плану, случайности не случайны и т.д. Почему это не так, мы разбирали в предыдущей статье «Квантовая случайность против детерминизма». Но быть может, непредсказуемы только квантовые процессы, а в масштабах классического макромира они не играют никакой роли? Нет – отвечают теория хаоса, синергетика и другие «нелинейные» науки. Хотя, как однажды заметил математик Станислав Улам, «использование такого термина, как «нелинейная наука», равносильно тому, чтобы называть большую часть зоологии исследованием животных, не являющихся слонами». То есть линейные, детерминированные и предсказуемые процессы являются скорее исключением, ��ем правилом, в нашем хаотическом мире.
Синергетика появилась в результате объединения двух разделов физики: неравновесной термодинамики и статистической механики необратимых процессов. Её основы были заложены научно-исследовательской деятельностью Брюссельской школы во главе с Ильёй Пригожиным (1917-2003), который в 1947 г. доказал свою знаменитую теорему о минимальном производстве энтропии в линейной неравновесной системе. Родоначальником именно синергетики считается немецкий физик, профессор штутгартского университета, специалист по нелинейной оптике Герман Хакен (род. 1927): в 1973 г. слово «синергетика» прозвучало в его докладе «Кооперативные явления в сильно неравновесных и нефизических системах». Но сам термин «синергетика» (от др-греч. συν и ἔργον – «совместная деятельность, содействие») придумал ещё в 1927 г. американский архитектор и философ Ричард Бакминстер Фуллер (1895–1983). В 1974 г. был опубликован первый из двух томов его книги «Синергетика: исследования в области геометрии мышления», суммировавшей исследования, проведенные за всю его жизнь. Датой рождения синергетики как науки можно считать 1977-й год, когда вышла книга Германа Хакена «Синергетика», Илья Пригожин получил Нобелевскую премию по химии за вклад в изучение диссипативных структур в термодинамических системах, далёких от равновесия, а Нью-Йоркская академия наук организовала первый симпозиум по хаосу. В 1978 г. старейший и крупнейший форум физиков – Сальвеевский конгресс – был полностью посвящён проблемам самоорганизации.

На постсоветском пространстве пользуется популярностью термин «постнеклассическая наука», предложенный в 90-е гг. Вячеславом Семеновичем Стёпиным по аналогии с постнеклассической философией. Поклонники Томаса Куна говорят о целой нелинейной синергетической парадигме, осуществляющей синтез научного знания. Дескать наука стала слишком специализированной, редукционистской и несогласованной, поэтому пришло время вырабатывать универсальные, холистические, обобщённые системные подходы и «теории всего», применимые как в естественных отраслях, так и в гуманитарных. Начиная с 1920-х гг. появляются междисциплинарные, околонаучные и философские направления разной степени фальсифицируемости, претендующие на то, чтобы объяснить всё на св��те: тектология Александра Богданова, общая теория систем Людвига фон Берталанфи, переосмысленная гегелевская диалектика, теория аутопоэзиса Никласа Лумана, системогенетика (А.И. Субетто), универсальный эволюционизм (Н.Н. Моисеев), концепция универсальной истории (А.П. Назаретян); психофрактальная эволюция социумов (Е.А. Донченко); ритмокаскадная модель развития (В.Г. Буданов) и т.д. Но самое видное место в этом ряду занимает синергетика, о которой речь пойдёт в данной статье.
Синергия и системный эффект
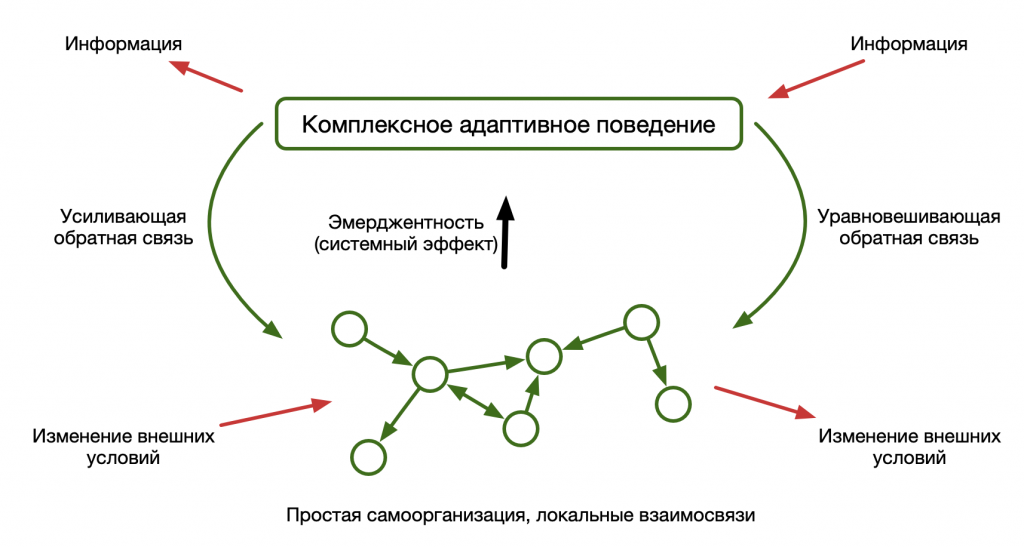
Начнём мы объяснение принципов синергетики с системного подхода. В самом общем определении система – это целостный комплекс взаимосвязанных элементов. В отличие от простого множества отдельных элементов, система имеет упорядоченные внутренние связи между её частями, то есть некую иерархическую структуру, и взаимодействует со средой как единое целое. Но главным признаком системы является несводимость свойств системы к сумме свойств её элементов – системный эффект, или эмерджентность. Грубо говоря, в системе 1+1 всегда равно больше 2. Это свойство систем описывал еще Аристотель в своей «Метафизике»: «целое больше, чем сумма его частей». С эмерджентностью тесно связано понятие синергии – совместного действия нескольких факторов, которое существенно превосходит простую сумму действий каждого из этих факторов. Отсюда и название междисциплинарной науки.

Любой макроскопический объект можно рассматривать как систему, состоящую из большого множества элементов и подсистем (молекул, атомов, элементарных частиц). Если объект обладает ненулевой энтропией (т.е. не охлаждён до абсолютного нуля), он является динамической системой, для которой можно установить функциональную зависимость между временем и положением каждого её элемента в фазовом пространстве. Иначе говоря, реальные физические системы всегда изменяются во времени, поскольку частицы, из которых они состоят, движутся. В динамических системах постоянно происходят флуктуации – случайные отклонения состояний их элементов и подсистем. Как станет ясно чуть позже, они играют ключевую роль в возникновении нового порядка и усложнении.
Закрытая система, не взаимодействующая со средой и не получающая энергию извне, в соответствии с законами термодинамики стремится к состоянию с максимальной энтропией – тепловому равновесию. В таком состоянии эволюция сколь угодно сложной системы прекращается. Но есть и другие, открытые системы, которые обмениваются энергией и информацией с окружающей средой. К таким системам неприменимы формулы классической термодинамики, включая закон неубывания энтропии, который по определению описывает только изолированные (закрытые) системы. Подробнее мы разбирали этот вопрос в статье «Правда и мифы об энтропии».
В динамически стабильных системах, которые развиваются линейно и предсказуемо, флуктуации подавляются с помощью механизма отрицател��ной обратной связи. Это когда выходной сигнал системы уменьшает действие входного сигнала, обеспечивая сохранение устойчивой структуры и состояния системы, близкого к равновесию. По принципу отрицательной обратной связи работают почти все автоматические устройства, от бачка унитаза до системы управления ядерным реактором. Все они являются примерами адаптивных систем, способных изменять свою структуру, подстраиваться под условия среды и учиться на собственном опыте. Сложные адаптивные системы (CAS) изучает наука об управлении – кибернетика, а также теория сложности. Под сложностью (complexity) системы в данном случае подразумевается, что она состоит из большого количества и разнообразия взаимозависимых, но автономных частей. Примерами сложных адаптивных систем являются живые организмы и роботы, которые получают обратные сигналы от рецепторов или датчиков относительно своего положения и корректируют положение к исходному состоянию исполнительными механизмами.
Диссипативные системы и самоорганизация
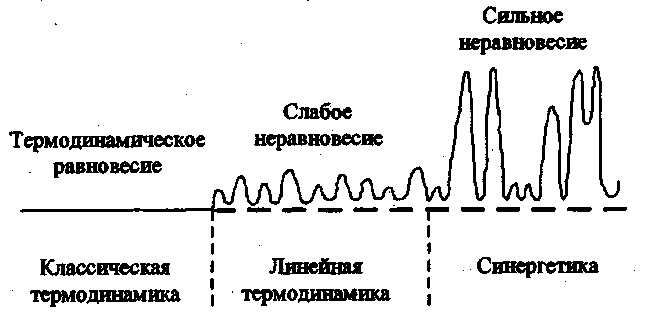
С точки зрения синергетики наибольший интерес представляют диссипативные системы, которые поглощают извне большое количество высоко упорядоченной энергии (электрического тока, света, кинетической энергии воздушных или водяных потоков) и отдают её назад в виде тепла. Их ещё называют неравновесными открытыми системами, потому что они могут сохранять устойчивое состояние в неравновесной среде за счёт диссипации (от лат. dissipatio — «рассеиваю, разрушаю») поступающей энергии. Диссипативные системы развиваются нелинейно и непредсказуемо, совершая фазовые переходы из неупорядоченного в упорядоченное состояние и обратно. В математике и естественных науках линейность означает, что система должна изменяться пропорционально изменению некой переменной. Соответственно нелинейность – это изменение выходных данных не пропорционально изменению входных данных. Например, в линейной стереосистеме вы поворачиваете регулятор громкости на одну единицу – громкость увеличивается на одну единицу. Но если вы повернёте регулятор громкости слишком резко, громкость может увеличиться больше, чем на количество единиц поворота, и вдобавок звук будет искажён – это уже нелинейный ответ.
Только диссипативные системы способны к спонтанной самоорганизации. По определению Германа Хакена, «Самоорганизация — процесс упорядочения (пространственного, временного или пространственно-временного) в открытой системе, за счёт согласованного взаимодействия множества элементов её составляющих». Самоорганизация означает резкое уменьшение количества степеней свободы (энтропии) системы, что сопровождается увеличением макроскопического «порядка» (формированием паттернов), который не зависит от микроскопических деталей взаимодействия подсистем. У диссипативной системы есть два стационарных устойчивых режима: а) хаотический, в котором элементы взаимодействуют некогерентно (не согласованно) и б) упорядоченный, в котором элементы ведут себя когерентно (согласованно), даже если это обнаруживается только на микроскопическом уровне. Самые простые примеры самоорганизующихся систем – ячейки Бенара или фигуры Хладни. Более сложные примеры – лазеры, капельный кластер, периодическая реакция Белоусова-Жаботинского, клубы дыма, циркуляция атмосферы и, наконец, биологическая жизнь.
В самоорганизующейся системе, по выражению Пригожина, возникает «порядок из хаоса»: вследствие случайных флуктуаций элементы спонтанно синхронизируют свои движения и образуют упорядоченную структуру, которая в дальнейшем начинает подавлять флуктуации с помощью механизма отрицательной обратной связи, защищая себя от разрушения. В неравновесных условиях относительная независимость элементов системы уступает место коооперации элементов: вблизи равновесия элемент взаимодействует только с соседними, вдали от равновесия – «видит» всю систему целиком и действует согласованно с другими элементами. Но возникновение и поддержание порядка всегда происходит за счёт увеличения хаоса (энтропии) окружающей среды. Так закон роста энтропии в целом соблюдается, но природа как бы находит в нём «лазейку» и создаёт локальную упорядоченность.
Для возникновения локальной упорядоченности и самоорганизации нужны особые условия:
Система должна быть достаточно сложной, то есть состоять из большого количества взаимодействующих между собой элементов и обладать высокой амплитудой флуктуаций;
Система должна быть открытой, то есть свободно обмениваться энергией и веществом с внешней средой;
Система должна быть неравновесной, то есть находиться далеко от точки термодинамического равновесия с окружающей средой.
При соблюдении всех этих условий срабатывает механизм, напоминающий диалектический закон перехода количества в качество: постепенное накопление необратимых количественных изменений приводит к катастрофе или резкому качественному скачку на новый уровень организации. Здесь вступает в силу математический аппарат теории катастроф, разработанной в конце 1960-х — начале 1970-х гг. математиками Рене Томом, Кристофером Зиманом и Владимиром Арнольдом. Термин «катастрофа» в этой теории означает резкое качественное изменение объекта при плавном количественном изменении параметров, от которых он зависит. То есть катастрофой можно назвать не только разрушение, но и любую трансформацию объекта, полностью изменяющую его свойства. Другие термины, позаимствованные синергетикой из теории катастроф – это бифуркация, аттрактор, неустойчивость, режим с обострением и фазовый переход. Их также использовали математики А.А. Самарский и С.П. Курдюмов, развивая свою теорию нестационарных структур в режимах с обострением.
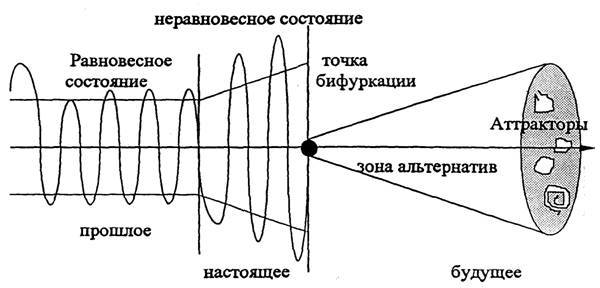
Когда динамическая система входит в неустойчивый режим с обострением, начинают преобладать положительная обратная связь, при которой выходной сигнал усиливает входной. Из-за этого возникшие в ходе флуктуаций изменения не подавляются, а со временем накапливаются и возрастают, расшатывая прежний порядок. Система проходит через кратковременное хаотическое состояние, что приводит либо к разрушению её структуры, либо к возникновению нового порядка и новых структур. Критический момент, когда система находится на распутье перед несколькими возможными исходами, называется точкой бифуркации. Бифуркация — это скачкообразная качественная перестройка структуры системы при плавном изменении еë параметров.

Поскольку флуктуации по своей природе случайны, состояние системы после бифуркации предсказать невозможно. Как пишет Пригожин,
«любое описание системы, претерпевающей бифуркации, включает и детерминистический, и вероятностный элементы (…) между двумя точками бифуркации в системе выполняются детерминистические законы, например, законы химической кинетики, но в окрестностях точек бифуркации существенную роль играют флуктуации, и именно они «выбирают» ветвь, которой будет следовать система».
«В макроскопической физике флуктуации, как правило, не играют заметной роли и входят только в небольшие поправки, которыми допустимо пренебречь, если система достаточно велика. Однако вблизи бифуркаций флуктуации приобретают решающее значение, так как в окрестностях точек бифуркации средние определяются именно флуктуациями. Именно в этом состоит суть понятия порядка через флуктуации».
Аттракторы в фазовом пространстве
Для моделирования поведения динамической системы всю бесконечность её возможных состояний представляют в виде пространства точек – фазового пространства. Каждая точка фазового пространства представляет данную систему в кратчайшем временном отрезке. В каждой точке концентрируются все известные данные о системе за каждый момент времени. Обычно достаточно всего двух переменных: положения системы в пространстве и скорости (импульса). Всю эволюцию системы можно изобразить на графике, следя за перемещениями точки с течением времени и наблюдая за ее траекторией в фазовом пространстве. В этом пространстве обязательно обнаружатся траектории, которые система предпочитает любым другим. Все вместе они образуют аттрактор – множество точек в фазовом пространстве, к которому стремится динамическая система с течением времени. На более простом языке аттрактор можно понимать как состояние, к которому стремится система и которое определяет траекторию её движения. Вот как описывает его Илья Пригожин:
«При исследовании того, как простое относится к сложному, мы выбираем в качестве путеводной нити понятие "аттрактора", то есть конечного состояния или хода эволюции диссипативной системы… Идеальный маятник (без трения) не имеет аттрактора и колеблется вечно. С другой стороны, движение реального маятника - диссипативной системы, движение которой включает трение, - постепенно останавливается в положении равновесия. Это положение является аттрактором: как известно, при любой начальной скорости и любом начальном положении маятник по истечении достаточного времени будет обнаружен покоящимся в состоянии равновесия. Аналогичным образом, является аттрактором и состояние термодинамического равновесия: популяция из миллиардов и миллиардов частиц, образующих изолированную систему, эволюционирует к состоянию равновесия, описание которого зависит лишь от немногих параметров, таких, как температура и давление». (И. Пригожин «Время, хаос, квант»)

Выделяют следующие типы аттракторов:
Точечный – направляет систему к единственному состоянию по прямой линии (одномерная траектория).
Циклический – определяет движение вперёд-назад, притяжение-отталкивание, смену двух противоположных состояний.
Аттрактор Торас – задаёт более сложную циркуляцию, повторяющую себя по мере движения вперёд. Может быть представлен в виде замкнутого кольца, бублика, трёхмерной спирали или вихря.
Странный – аттрактор, организующий на первый взгляд хаотичное поведение системы и оставляющий ей большую свободу выбора. Является четырёхмерным аналогом фрактального множества Мандельброта.
Скрытый – сосуществует с устойчивым состоянием равновесия, его область притяжения не пересекается с открытой окрестностью точек равновесия, поэтому выбор начальных данных для его визуализации не очевиден. В 2009 г. был обнаружен скрытый аттрактор в простейшей электрической цепи Чуа с одним нелинейным резистором, демонстрирующей режимы хаотических колебаний.
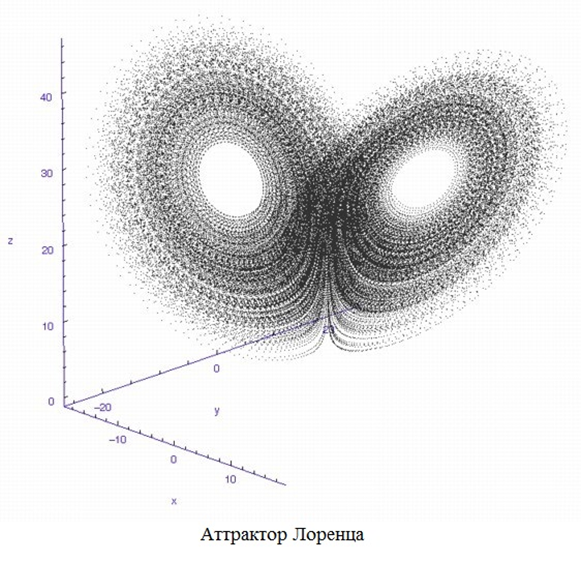
Для простой механической системы вроде падающего на землю камня все траектории сведутся к одной нижней точке – равновесному состоянию с максимальной энтропией. Это будет точечный аттрактор. Есть системы, которые непрерывно повторяют одни и те же движения, как планеты, вращающиеся по орбитам вокруг звезды (если пренебречь потерями энергии через гравитационные волны) – это циклический аттрактор в виде замкнутой кривой. У диссипативной системы поведение сложнее: она может менять траекторию в точках бифуркации и поочерёдно стремиться к разным состояниям. Для моделирования её поведения используется понятие странного аттрактора – притягивающего множества неустойчивых траекторий в фазовом пространстве диссипативной системы. Такой аттрактор имеет фрактальную структуру и может принимать довольно причудливую форму. Например, странный аттрактор Лоренца представляет собой две фрактальные спирали, смещённые в пространстве и соединённые в знак бесконечности, наподобие ленты Мёбиуса. Ещё один странный аттрактор – соленоид Смейла-Вильямса – напоминает четырёхмерную бутылку Клейна.

Теория хаоса и эффект бабочки
Для описания поведения нелинейной динамической системы в неустойчивом режиме используется математический аппарат теории хаоса. Последователи Хакена считают её разделом синергетики, а в США и других англоязычных странах – наоборот, называют синергетику ответвлением теории хаоса. Как бы то ни было, теория хаоса — раздел математики, изучающий поведение детерминированных динамических систем, где решения имеют достаточно сложную структуру, поэтому кажется, что во времени они ведут себя случайным образом. В этой теории есть понятие динамического, или детерминированного хаоса. Джеймс Глейк приводит шесть разных определений хаоса от первооткрывателей этого явления:
сложные апериодичные динамические системы, обычно с малым числом измерений (Филип Холмс, математик из Корнелла);
тип порядка, которому несвойственна периодичность, а также: быстро развивающаяся область исследований, в которую внесли важный вклад математики, физики, специалисты по гидродинамике, экологи, или: недавно признанный и повсеместно встреч��ющийся класс естественных явлений (Хао Бай-Линь, китайский физик);
явно беспорядочное, повторяющееся поведение в простой детерминистской системе, похожей на работающие часы (Х. Брюс-Стюарт, математик из Брукхевенской национальной лаборатории на Лонг-Айленде);
иррегулярное и непредсказуемое поведение детерминистских нелинейных динамических систем (Родерик В. Дженсен, физик-теоретик из Йельского университета);
динамика с положительной, но ограниченной метрической энтропией, что в переводе с языка математики звучит следующим образом: поведение, которое порождает информацию (усиливает малые неопределенности), но не является полностью предсказуемым (Джеймс Кручфилд из университета Санта-Круз);
динамика, сбросившая наконец оковы порядка и предсказуемости… системы, каждую динамическую возможность которых теперь можно свободно рассматривать… разнообразие, которое будоражит, богатство выбора, изобилие вероятностей… (Джозеф Форд, «проповедник хаоса»)
Независимо от того, какое определение вы предпочтёте, у хаоса есть набор характерных признаков. В таком состоянии поведение системы кажется случайным и неупорядоченным, несмотря на то, что оно определяется детерминистическими законами. Система выглядит хаотичной на макроскопическом масштабе, потому что её упорядоченность скрыта на микроуровне. Детерминированный хаос можно обнаружить во многих природных явлениях, начиная с турбулентных потоков в атмосфере и заканчивая динамикой численности биологических популяций. Теорию хаоса используют для моделирования ураганов, турбулентности, движения потоков жидкости, частоты падения капель из подтекающего крана, эволюции шаровых звёздных скоплений и галактик, сейсмической активности, прогнозирование данных фондовой биржи, сердечных аритмий, распространения эпидемий и т.д.

У всех перечисленных систем есть общее свойство: незначительное воздействие на систему может иметь большие и непредсказуемые последствия, в том числе в совершенно другом месте. Речь идёт об эффекте бабочки, который по-научному называют «сильной зависимостью от начальных условий». Первым его упомянул французский математик Анри Пуанкаре в своём исследовании задачи о движении трёх тел в 1890 г.: «небольшие различия в начальных условиях рождают огромные различия в конечном явлении… Предсказание становится невозможным». В популярном представлении эффект бабочки ассоциируется с путешествиями во времени: в фильме «Эффект бабочки» (2004) главный герой возвращался в своё прошлое, изменял в нём незначительные детали и получал непредсказуемые, радикальные изменения в настоящем, а в знаменитом рассказе Рэя Брэдбери «И грянул гром» (1952) один персонаж полностью меняет будущее, просто наступив на бабочку во время экскурсии в эпоху динозавров. На самом деле эффект бабочки может проявляться и на более коротких отрезках времени. Хорошей его иллюстрацией является сказка «Репка»: чувствительность к начальным условиям формируется детерминированно, а спусковым крючком или триггером может послужить самый незначительный фактор.

Эффект бабочки открыл американский метеоролог Эдвард Лоренц, пытаясь осуществить долгосрочный прогноз погоды. В 1963 г. он опубликовал в журнале Journal of the Atmospheric Sciences статью «Детерминированное непериодическое течение», заложившую основы теории хаоса. Вы наверняка уже слышали историю о том, как Лоренц моделировал на ЭВМ динамику воздушных потоков в атмосфере, решая набор из 12-ти уравнений. Однажды он остановил вычисление на середине и ввёл полученные значения в качестве начальных условий, но компьютер ради экономии ресурсов округлил числа с шести до трёх знаков после запятой (например, вместо 0.0506127 напечатал 0.506). В результате программа решила уравнения совсем по-другому, и полученный график сильно отклонялся от первоначального. Поскольку начальные условия (температуру и давление в каждой точке атмосферы) невозможно измерить с бесконечной точностью, Лоренц пришёл к выводу, что долговременное предсказание погоды невозможно. В хаотическом мире трудно предсказать, какие вариации возникнут в данное время и в данном месте, ошибки и неопределённость нарастают экспоненциально с течением времени.

Словосочетание «эффект бабочки» связывают не только с удачной метафорой Лоренца, вынесенной в название его доклада 1972 г. «Вызывает ли взмах крыльев бабочки в Бразилии торнадо в Техасе?», но и с характерной формой аттрактора Лоренца, напоминающей крылья бабочки. Этот аттрактор иллюстрирует эффект бабочки как перемешивание фазового пространства: чувствительность к начальным условиям приводит к тому, что при попытке рассчитать движение системы из двух очень близких начальных состояний, решения уравнений, неотличимые вначале, различаются всё сильнее и сильнее, пока не разойдутся окончательно. Аттрактор Лоренца описывает медленное хаотичное вращение конвекционных потоков жидкости попеременно то в одном, то в другом направлении. Это устойчивый непериодический странный аттрактор с тремя независимыми переменными. Вся его прелесть заключается в том, что его петли и спирали кажутся бесконечно глубокими, потому что никогда до конца не соединяются и не пересекаются. Тем не менее, бесконечное множество траекторий помещается в ограниченном трёхмерном пространстве. Как такое возможно?

Возможно, если вспомнить необычные свойства фракталов. Фракталы имеют дробную разм��рность и обладают самоподобной структурой: сколько бы вы не увеличивали масштаб, один и тот же паттерн будет повторяться снова и снова, часть всегда идентична или подобна целому. Странные аттракторы хаотических моделей как раз имеют бесконечное количество слоёв повторяющейся структуры, что позволяет траекториям оставаться в пределах ограниченной области пространства состояний, складываясь и переплетаясь друг с другом, никогда не пересекаясь и не повторяя себя в точности. В данном случае фрактальную структуру имеет как сам процесс самоорганизации (траектории движения системы в фазовом пространстве), так и его результат (форма самой диссипативной структуры). Поэтому теория хаоса не может обойтись без фрактальной геометрии Бенуа Мандельброта, которая сводит сложные самоподобные структуры к коротким рекурсивным функциям. Но фракталы – слишком интересная тема, чтобы не посвятить ей отдельную статью.
Квантовый хаос
Связь между классическим хаосом и квантовой механикой изучает малоизвестный и далеко не общепризнанный раздел физики под названием квантовая хаология. Дело в том, что само существование квантового хаоса пока ещё под вопросом. В теории классического хаоса не существует нижнего предела того, насколько малыми могут быть некоторые изменения или возмущения – малейшие эффекты в конечном итоге будут усиливаться, влияя на поведение любой системы, чувствительной к начальным условиям. В связи с этим некоторые авторы допускают, что случайные квантовые флуктуации могут «заразить» хаотические системы классической механики. Сформулированная ими гипотеза квантового хаоса звучит так: «короткодействующие корреляции в энергетических спектрах квазиклассических квантовых систем, сильно хаотичных в классическом пределе, подчиняются универсальным законам флуктуаций, основанным на ансамблях случайных матриц без свободных параметров». Но на сегодняшний день есть аргументы как «за», так и «против» данной гипотезы.
С одной стороны, в основе классического хаоса должны существовать квантовые механизмы. Это следует из принципа соответствия, согласно которому классическая механика является предельным случаем квантовой механики, когда отношение постоянной Планка к действию системы стремится к нулю. Джозеф Форд предложил другую интерпретацию этого принципа: «Любые две действительные физические теории, области действия которых пересекаются, должны с соответствующей точностью давать одни и те же предсказания для физических наблюдений». В случае квантовой и ньютоновской механики это означает, что «квантовая механика должна в целом согласовываться с предсказаниями ньютоновской механики, когда изучаемые системы являются макроскопическими». По мнению Форда, «сама суть соответствия заключается в идее, что квантовая механика может описывать события в макроскопическом мире без каких-либо ограничений. Если бы это было не так, то не было бы пересечения квантовой и классической областей достоверности».

С другой стороны, в квантовой механике нет ничего похожего на экспоненциальную чувствительность к начальным условиям, и для её возникновения в классическом хаосе нет никаких оснований. Во-первых, классический хаос характеризуется нелинейностью, тогда как уравнение Шрёдингера, описывающее эволюцию квантовых систем, является линейным. Во-вторых, пространство состояний классической системы поддерживает фрактальную структуру, а пространство состояний квантовой системы – нет. В реальных физических системах не существует по-настоящему странных аттракторов с фрактальной размерностью, возможны только предфрактальные аттракторы с самоподобием в конечных пространственных масштабах. Это исключает наличие бесконечного числа степеней свободы системы и бесконечную точность измерения начальных условий. В-третьих, рассмотрение смешанных квантовых состояний как фактически классических, с точным состоянием системы, неизвестным наблюдателю – это пережиток копенгагенской интерпретации, делившей мир на квантовый и классический. Сегодня переход чистого состояния в смешанное называют декогеренцией, которая является линейным и унитарным процессом.
В 2020 г. группа исследователей под руководством Николая Синицына из Лос-Аламосской национальной лаборатории провела эксперимент, доказавший отсутствие эффекта бабочки в квантовой механике. Учёные смоделировали на квантовом компьютере IBM-Q «путешествие в прошлое», повернув вспять эволюцию системы запутанных кубитов. Затем они сильно повредили один из кубитов, вернули систему в «настоящее» и провели измерение. Оказалось, что повреждение в прошлом вызывает лишь локальные и несущественные изменения в настоящем, тогда как в хаотичной макроскопической системе незначительное влияние в начале может повлечь большие и непредсказуемые последствия в конце. Следовательно, эффект бабочки в квантовой механике не работает. Это хорошо в случае, если злоумышленник выполнит измерения, наносящие ущерб сильно запутанному состоянию кубитов: получатель всё равно сможет легко восстановить полезную информацию, поскольку ущерб не увеличивается в процессе декодирования. Но нас больше интересует теоретический аспект исследования: откуда берётся хаос в макромире, если его нет в микромире?
Вроде бы известно немало относительно простых макроскопических систем с нелинейной динамикой, которые считаются классическими и детерминированными. Это колебание двойного маятника, бросание монетки и, конечно же, проблема трёх тел. Анри Пуанкаре обнаружил, что в системах из 3-х и более гравитационно связанных тел незначительное изменение начальных условий (положения и скорости) приводит к тому, что траектории тела очень быстро удаляются друг от друга. Существует множество частных решений задачи трёх тел, но аналитического решения для общего случая не существует. Динамическая система трех тел, вращающихся вокруг друг друга, хаотична для большинства начальных условий, и в большинстве случаев единственный способ определить их положения — это рассчитать их с помощью численных методов. Поэтому предсказать поведение системы из трёх звезд можно лишь с некоторой точностью и до некоторого момента, при этом наша возможность ��редсказывать упирается только в доступную точность измерений начальных условий. Незначительная разница в точности измерений может быть вызвана фоновым шумом, тепловыми флуктуациями, неисправностью оборудования и другими факторами, которых практически невозможно избежать. Как показывают недавние исследования, даже слабого молекулярного шума достаточно, чтобы вызвать эффект бабочки. Следовательно, не существует систем, которые не подвержены влиянию случайных квантовых флуктуаций, и эти флуктуации и являются причиной макроскопического хаоса.
Так всё-таки хаос детерминирован или нет? Отчасти детерминирован, а отчасти случаен.

Давайте снова посмотрим на аттрактор Лоренца. Математик сразу увидит в нём бинарность решений системы нелинейных дифференциальных уравнений, которые при разных входных параметрах стремятся к одному из «крыльев» аттрактора. Система способна непредсказуемо перепрыгивать от одного «крыла» аттрактора к другому (например, из нормального климата в ледниковый период и обратно) вследствие незначительных изменений исходных параметров. Если разница в начальных условиях обусловлена квантовыми эффектами, система абсолютно недетерминирована. Однако все решения уравнений группируются вокруг двух зон притяжения – «крыльев» аттрактора, система никогда не выйдет за пределы этих областей. Следовательно, два возможных исхода эволюции детерминированы, но какой из них «выберет» система, оказавшись в точке бифуркации – дело случая.
Ок, но как это согласуется с отсутствием эффекта бабочки в квантовой механике и с детерминированной эволюцией волновой функции? Для ответа на этот вопрос нам не обойтись без многомировой интерпретации Эверетта, которая даёт более наглядное представление хаотических процессов. Действительно, в масштабах отдельных частиц чувствительности к начальным условиям нет, их взаимодействия линейны и детерминированы. Случайным считается только результат квантового измерения с точки зрения наблюдателя, однако в теории Эверетта это обусловлено вполне детерминированным ветвлением самого наблюдателя на копии, существующие в параллельных мирах. В нашем случае наблюдатель вообще ни при чём, поскольку речь идёт об эволюции чистого состояния изолированной системы. Если система состоит из огромного количества частиц, внутри неё царит настоящий квантовый хаос, но этот хаос линейный и не распространяющийся на макромасштабы: тепловые флуктуации компенсируют друг друга и усредняются.

В некоторых версиях многомировой интерпретации это выглядит так, как если бы ветви волновой функции расщеплялись и почти сразу «склеивались», не разрастаясь до полноценных параллельных миров. Другие эвереттианцы считают, что такое «склеивание» возможно только в контролируемых условиях (например, на квантовом компьютере), а в нашем случае квантовая интерференция в системе отсутствует, поэтому миры расщепляются навсегда. С другой стороны, понятие «ветви» волновой функции или синглвёрса по большому счёту произвольно, мы можем делить реальность на любое количество ветвей, опуская незаметные детали. Тогда совокупность едва различающихся между собой «мелкозернистых» параллельных миров будет выглядеть как единая ветвь Мультивселенной на «крупнозернистом» масштабе. И на этом масштабе мы увидим, что в точке бифуркации одна классическая вселенная разделилась на две, соответствующие двум «крыльям» аттрактора Лоренца. Затем происходит каскад дальнейших ветвлений, и получается, что одна незначительная причина (квантовая «бабочка») вызывает разнообразные и значительные следствия (ураган или его отсутствие). А на «мелкозернистом» масштабе множество «тонких», почти равновероятных ветвей, линейно переходит в такое же множество ветвей. Здесь бабочка уже не является причиной урагана: взмах её крыла мог запустить, а мог и не запустить каскад ветвлений, к тому же на месте бабочки с таким же успехом могли оказаться стрекоза или майский жук. В любом случае процесс ветвление вселенной детерминирован, а иллюзия случайности возникает из-за того, что наблюдатель не знает, в какой ветви он оказался. Подробнее о неопределённости самолокации я рассказывал в статье «Проблема измерения».
Роль синергетики в объяснении абиогенеза и эволюции
О современной гипотезе диссипативной адаптации, объясняющей происхождение жизни и дарвиновскую эволюцию с помощью неравновесной термодинамики, у меня будет отдельная статья. А пока мы проследим истоки этой идеи в работах теоретиков хаоса.
В 1981 г. Роберт Шоу в статье «Странные аттракторы: хаотическое поведение и поток информации» сделал первую попытку объединения теории хаоса и теории информации. Он пересмотрел некоторые предположения классической механики и пришёл к выводу, что странные аттракторы являются эффективными смесителями, которые создают непредсказуемость, повышая тем самым энтропию, и порождают информацию там, где её ранее не существовало. С точки зрения Шоу, хаотические системы позволяют преодолеть разрыв в предсказаниях между ньютоновской механикой и термодинамикой, когда суммарная энергия микромасштабов превышает энергию макромасштабов. Классической механика описывает макрообъекты без учёта их температуры, трения и т.д., а термодинамика характеризует движение неисчислимого количества молекул усреднёнными данными, такими как температура, давление и т.д.
Тем временем советские учёные Андрей Колмогоров и Яков Синай разработали математические методы, позволяющие связать удельную энтропию системы (энтропию на единицу времени), с геометрическими изображениями растягивающихся и сгибающихся в фазовом пространстве поверхностей. Изменения площади соответствовали внесению неопределенности относительно прошлого системы, получению или утрате информации.
«Каким-то образом по мере движения Вселенной к конечному равновесию в лишённом характерных черт пекле максимальной энтропии появляются удивительные структуры. Вдумчивые физики, соприкасающиеся с действием термодинамики, понимают, насколько волнующим является вопрос, который один из них сформулировал следующим образом: «Как бесцельный поток энергии может привносить жизнь и сознание в наш мир?» Решить проблему помогает весьма расплывчатое понятие энтропии, вполне приемлемое и хорошо определенное для целей термодинамики, когда речь идет о нагреве и температуре, однако чертовски сложное для того, чтобы его можно было ассоциировать с мерой беспорядка» (Джеймс Глейк, «Хаос. Создание новой науки»)
Илья Пригожин тоже неоднократно намекал, что неравновесная термодинамика является ключом к пониманию процесса абиогенеза, т.е. возникновения жизни из неорганической материи:
«По-видимому, большинство биологических механизмов действия свидетельствуют о том, что жизнь сопряжена с далёкими от равновесия условиями за порогом устойчивости термодинамической ветви. В этой связи невольно напрашивается мысль, что происхождение жизни может быть связано с серией последовательных неустойчивостей, аналогичных серии последовательных бифуркаций, которая привела к состоянию вещества с повышенной когерентностью».
Более того, Брюссельская школа Пригожина рассматривала неравновесную термодинамику как универсальную теорию эволюции, применимую к любым сложным системам во Вселенной. Действительно, открытые ею принципы распространяются практически на все сферы знания, включая биологическую теорию эволюции. Но не следует переоценивать синергетику и применять её математический аппарат к явлениям, не поддающимся количественному измерению, или слишком сложным для компьютерного моделирования. Этим грешил даже Герман Хакен, рассуждая в своей книге «Тайны природы. Синергетика: учение о взаимодействии» о возможности предсказания вооружённых конфликтов и революций. Очевидно, биологические и социальные системы намного сложнее тех диссипативных структур, поведение которых описывает синергетика. Одних только формул неравновесной термодинамики будет недостаточно, чтобы смоделировать развитие человеческой популяции, динамику экономического роста или исход войны. Поведение людей гораздо сложнее поведения атомов и молекул, поэтому математический аппарат синергетики едва ли применим к социальным, экономическим, историческим или психологическим процессам. Что не мешает активным сторонникам «новой парадигмы» свободно подгонять свою теорию под факты, проводить поверхностные аналогии и употреблять при каждой возможности синергетическую терминологию, значения которой всё равно никто не понимает.
Псевдосинергетика
Некоторые синергетики заходят ещё дальше и ступают на поле философских рассуждений, весьма далёких от науки. Так, представители российской синергетической школы во главе с Сергеем Курдюмовым занимались поисками спектров эволюционных форм – дискретного множества наиболее устойчивых структур, которые природа предпочитает всем остальным. Я ничего не имею против Курдюмова и признаю его научный вклад в изучение сложных адаптивных систем, но написанные им в соавторстве с философом Еленой Князевой книги и статьи переполнены весьма сомнительными утверждениями. По-видимому, не сильно разбираясь в Стандартной модели квантовой теории поля, учёные стали задавать вопросы вроде: почему атомов порядка сотни, а не, скажем, существенно больше или меньше? почему существует дискретный набор зарядов ядер атомов, спектр типов атомов? почему заряды целочисленны? почему существуют только несколько типов астрофизических объектов (звёзды, галактики, скопления и сверхскопления галактик) и т.п. Естественно, на эти вопросы сразу нашлись «синергетические» ответы. Объясняя дискретность атомов и других физических объектов существованием «структур самоорганизации некой открытой нелинейной среды», особого «архитектурного каркаса» или «спектра эволюционных форм наблюдаемой Вселенной», российские синергетики связали это с понятием аттракторов и дошли до того, что отождествили их с платоновскими идеями:
«Природа имеет внутренние предпочтения к определенным формам живого и неживого. Только определённые наборы форм осуществимы в природных средах. А на другие формы наложен эволюционный запрет… Результаты синергетики как бы возвращают нас к идеям древних о потенциальном и непроявленном. В частности, они близки к представлениям Платона о неких первообразцах и совершенных формах в мире идей, уподобиться которым стремятся вещи видимого, всегда несовершенного мира. Или же к представлениям Аристотеля об энтелехии, о некой внутренней энергии, заложенной в материи, вынуждающей её к обретению определенной формы» (Князева Е. Н., Курдюмов С. П. «Эволюция вселенной с точки зрения синергетики»)
Так что же получается, синергетика возвращает нас к объективному идеализму и требует смены научной парадигмы? Нет, это очередной псевдонаучный миф. Аттракторы не существуют как физические объекты, это просто математические модели. И когда кто-то утверждает, что аттрактор определяет эволюцию нелинейной системы и «притягивает» к себе траекторию её движения, он путает причину со следствием. Будущего состояния системы ещё нет, оно не может влиять на настоящее. Это в настоящем система содержит в себе информацию о возможных путях своей эволюции. И на основе этой информации можно предсказать её поведение в будущем. С линейными системами это получается хорошо, они более-менее детерминированы. А вот нелинейные динамические системы, которые изучает синергетика, находятся в состоянии хаоса, что и отражают модели странных аттракторов. Предсказать поведение такой системы невозможно, потому что её судьба зависит от случайных квантовых событий.
Как же человеку, далёкому от науки, отличить «настоящую» синергетику от псевдосинергетики? Примерно так же, как и любое другое знание – об этом мы писали в статье «Критерии истины в эпоху постправды». Если теория научна, она даёт проверяемые предсказания, которые не противоречат предсказаниям других ��еорий, её трудно варьировать, и она включает в себя механизм собственного опровержения, т.е. является фальсифицируемой. Публикации по «настоящей» синергетике редко выходят за пределы рецензируемых научных журналов, изобилуют математическими формулами и решают преимущественно прикладные задачи. А псевдосинергетика характеризуется такими признаками, как философское многословие, использование множества непонятных терминов («солитон-фоновые возбуждения фрактальных слоёв кристалла первичной материи, именуемого физическим вакуумом», «ψ-поля степеней себя», «человекомерные системы» и т.д.), сопоставление далёких и никак не связанных между собой категорий (например, частоты обращений планет вокруг Солнца с музыкальными интервалами, цветами и мировыми религиями) и ссылки на эзотерические концепции (астрологию, «тонкие энергии», торсионные поля и т.д.), а также провозглашение синергетики «новой научной парадигмой» или «универсальной теорией всего». Что касается сходства принципов самоорганизации с законами биологической и культурной эволюции, то оно является скорее аналогией, проистекающей из вычислительной универсальности, чем причинно-следственной связью.
Вывод
В рамках исследований хаоса учёные пришли к одному важному выводу: простые системы дают начало сложному поведению, а сложные системы порождают простое поведение. Это противоречит нашему интуитивному представлению о том, что причина и следствие должны быть соизмеримыми. Подобная ошибка свойственна конспирологам, которые ищут в каждой пандемии, войне или смерти известного человека следы заговора, ведь не могут же такие важные события быть результатом случайных и малозначимых факторов! В действительности же происходит всё по-другому: слабые и незаметные воздействия иногда вызывают серьёзные последствия, а значительные усилия по их преодолению могут ни к чему не привести. Например, одна-единственная мутация в геноме коронавируса и чья-то дурная привычка есть летучих мышей привели к пандемии COVID-19, которую с трудом остановили даже глобальный локдаун с массовой вакцинацией. Также у большого следствия может быть множество мелких причин, или у одной большой причины – множество мелких следствий.
И главный вывод. Фразу «порядок из хаоса» не нужно понимать так, что за любым хаосом на самом деле скрывается порядок, и что любой на первый взгляд хаотичный процесс в действительности упорядочен и детерминирован. Она означает лишь то, что все упорядоченные и сложные природные объекты, которые нас окружают, появились из хаоса в результате самоорганизации в нелинейных диссипативных системах. Хаос – неотъемлемая часть мироздания, но в условиях постоянного потока концентрированной энергии из него может возникнуть порядок, чтобы создать вокруг себя ещё больше хаоса. Энтропия открытой диссипативной системы может уменьшаться, если это способствует более эффективному рассеянию энергии и росту энтропии в окружающей среде. Это просто одно из следствий второго закона термодинамики, в нём нет ничего мистического и сверхъестественного. В следующих статьях я раскрою немаловажную роль хаоса для понимания природы сознания и того, как эмерджентные свойства макроскопических систем возникают из квантовой механики и почему мы не наблюдаем квантовых эффектов в макромире.
