
Времена когда горящий куст мог принести озарение давно прошли. Примитивный опыт уже не может стать источником открытий. А всё потому, что он обобщён и впитан в культуру человечества. И чтобы подключиться к мудрости предков нужно опереться на философию. В этой статье мы познакомимся с новым алгоритмом кластеризации и поверхностно затронем некоторые философские категории. Перевернём объективность в субъектность и обратно.
Инструменты кластеризации
Кластеризация — это поиск групп о которых ничего не известно (не путать с классификацией, т. е. с назначением класса элементам). Неизвестность разрешается перебором параметров.
Если известно k количество искомых групп, то можно применить метод k-средних (k-means). Такой алгоритм подбирает центры. Работает для сферических групп.
Если перед вами вытянулись колбаски, то можно применить плотностный алгоритм DBSCAN(ε, k) — задать размер области ε и сколько точек k должна содержать область. Если две точки касаются друг друга такими областями, тогда эти точки принадлежат одному кластеру.
В обоих случаях приходится перебирать параметры. Перезапуск затратен, и выбор варианта человеком субъективен. Вот было бы здорово исключить эту меру мер и собрать решение за один прогон.

В поисках универсалий
Поступай с другими так, как хочешь, чтобы поступали с тобой.
И если другой ответит взаимностью, то вы притянитесь. Подобное соединяется с подобным, а неравноправным отношениям стыд, срам и конец очереди.
Но позвольте! У нас же данные, а не человеки! Поэтому нам предстоит очеловечить точки, закрыть их от окружающего мира и тем самым превратить в субъектов.
Если из точки распространить шар, то можно будет посчитать сколько точек попало в шар и какой радиус этого шара. А если остановить рост этого шара на конкретной точке, то определится отношение к этой точке-соседу. У этого отношения будет две стороны, количественный ранг и качественное расстояние.

Рассмотрим отношение между A и B:
• Для A: A, B, C, E. Ранг AB = 2.
Расстояние d.
• Для B: B, C, D, A. Ранг BA = 4. Расстояние d.
Оба шара имеют одинаковый радиус d = d(AB) = d(BA), но ранги отличаются. В жизни так же, вы стоите напротив человека, а он напротив вас. Объективно между вами равное расстояние, мерь хоть от него, хоть от вас, но есть маленький субъектный нюанс. Два нюанса, его и ваш. Учтём их. Сотворим из точек субъектов и оценим чужое качество.
Итак, у нас две независимые точки A и B. И явная разница в окружении: у А 2 точки, а у B 4 точки. Из "глаз" A оценим чужое отношение так, как будто у B столько же точек. То есть посчитаем BA в единицах A: поделим d на 4 и умножим на 2. И наоборот, из "глаз" B — оценка AB = 4/2·d.

Второй способ оценки — через перенос и натягивание чужого шара.
Перенесём голубой шар в систему координат A, сохраняя количественные свойства шара (внутри должно быть 4 точки). Тогда шар увеличится, чтобы вместить A, B, C, E!
Для B тоже всё поменяется — только наоборот шар уменьшится до точек B, C (белым пунктиром).
Итого получены по две оценки чужого отношения каждым субъектом. Сравним эти оценки с изначальным радиусом AB=d.
Для A: количественная оценка уменьшилась до 2/4·d; качественная оценка увеличилась до AE, т. е. до четвёртого ранга d(A₄);
Для B наоборот: количественная оценка увеличилась до 4/2·d; качественная оценка уменьшилась до второго ранга d(B₂).
Каждая точка стала субъектом, у неё нет доступа к чужим радиусам, к качественным сторонам отношений других. Но при этом у них появились две оценки происходящего r/R·d(r) и d(R). Заметим, что если бы ранги совпадали r=R, то обе оценки были бы равны d. Выбрав наибольшую оценку, станет возможным отделить подобные от неподобных
Самое близкое из таких отношений и кристаллизуется в ребро. Образуется деревце, и поиск наиближайшего запустится снова. Так будет продолжаться до тех пор, пока все точки не соединятся.
Без всяких зацепок-параметров нам удалось создать формулу диалектического расстояния, отражающую суть отношений точек в пространстве. Объективность пространства перешла в субъектность точек и вывернулась обратно в объект-ребро. Пройдя двойное отрицание, абстрактное стало конкретным.
ДРУГ (druhg)
Взаимное опосредование точек друг другом снял вопрос параметров и их подбора. Получился детерминированный алгоритм. Вначале собираются двухточечные деревья рангом 2. Потом сгустки точек растут, соединяя соседей, пока всё не превратится в единое дерево. При этом выбросы (ранги 2) будут иметь последнюю очередь соединений.
Алгоритм идеален для первичного исследования данных (EDA) и для поиска глобальных выбросов.

Глобальный порядок, локальный расчёт

Создаётся видимость глобального порядка соединений. Но это не так.
Ребро a значительно меньше ребра b, но они не влияют друг друга. Главное чтобы они случились до ребра c.
Частичный порядок позволяет познавать мир локально и не требует знаний обо всех точках света. Что открывает возможность параллельных вычислений на ячейках сетки пространства.
Сложность вычислений
Может также показаться, что сравнение всех точек со всеми — это вычислительно затратная задача с квадратичной сложностью O(n²). А повторный запуск процесса поиска ближайшего соединения усложняет вычисление до O(n³). Но это не так.
Поиск глобального ближайшего заменяется на поиск субъектных ближайших и хранение этих оптимумов. Структура данных k-ближайших соседей упрощает алгоритмическую сложность до O(n logn).

Точность vs производительность
В настоящей реализации можно ускорить алгоритм, ограничив количество соседей max_ranking. Но тогда есть вероятность, что в соседи не попадут точки другого кластера. (На предыдущей картинке пятый тест был перезапущен по этой причине).
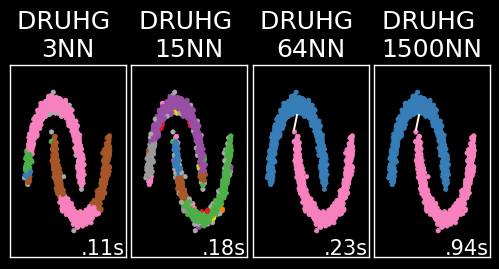
При ограничении от 6 до 63 ближайших соседей достигается хороший результат. После 64 соседей результат сходится и впустую тратится время обработки (возможно алгоритмически решится через поиск лучшего для дерева, а не точки).

Запуск и исследование вложенности
Жми сюда. Пример и код
Нажал сюда, нажми и на звёздочку с лайком.
https://github.com/artamono1/druhg/
# pip install druhg from druhg import DRUHG import matplotlib.pyplot as plt import pandas as pd, numpy as np XX = pd.read_csv('chameleon.csv', sep='\t', header=None) XX = np.array(XX) clusterer = DRUHG(max_ranking=200, do_edges=True) clusterer.fit(XX) # research tool with silders clusterer.plot() # manual labels labels = clusterer.relabel(exclude=[], size_range=[0.2, 2242], fix_outliers=1)
Первоначальный запуск дороговат. Но исследование вложенной структуры практически бесплатно. Можно экспериментировать:
Разбить кластер по его лейблу.
exclude=[7749] разобьёт красный огурецНе выводить слишком маленькие или слишком большие кластеры.
size_range=[0.2,2242] от 20% размера выборки до конкретных 2242. Слайдер Qty справа.Покрасить выбросы по соединённости.
fix_outliers=1.
Или запустить clusterer.plot():

Инструмент позволяет выбрать нужную разбивку по размеру кластеров — почему-то такой инструмент не предоставляется в стандартных инструментах. Позволяет выявлять глобальные выбросы. Получать общую информацию по кластеру. Наигравшись, можно сохранить результат через relabel().
P.S. о секретном соусе, превращающем деревья в кластеры, и о диалектике целостности расскажу в следующей статье.
