Начнем с резкого заявления: Математическая теория не подводила ИИ. Это ИИ не смог понять математическую теорию - а именно те разделы математики, которые напрямую влияют на интеллектуальные системы: теорию категорий, топологию, дифференциальную геометрию и структуры, связывающие их воедино.
Это различие крайне важно, потому что прямо сейчас «категориальный ИИ» становится модным способом рисовать стрелочки, чтобы звучать глуб��комысленно и при этом тихо игнорировать те самые вещи, которые делают интеллект по-настоящему сложным: время, память, историю и пути.
Если вы когда-нибудь задавались вопросом, почему ваш ИИ ведет себя во вторник иначе, чем в понедельник, хотя «ничего не менялось», - читайте дальше, здесь мы объясним почему. И это не баг. Это фундаментальная архитектурная слепота, которая уходит глубже, чем кто-либо готов признать.
Пристегнитесь. Мы начинаем!
1. Что на самом деле дает теория категорий (и ничего сверх того)
В своей основе теория категорий дает дисциплину. Не интеллект. Не смыслы. Именно дисциплину.
Объекты: состояния, пространства, типы
Морфизмы: трансформации
Композиция: то, как трансформации выстраиваются в цепи
Идентичность: понимание того, что на самом деле означает «ничего не делать»
Это важно. Без этого системы незаметно гниют. Теория категорий запрещает «магический клей», она принуждает к использованию четких интерфейсов и делает бессвязность вне закона.
Но давайте будем точны: теория категорий - это грамматика, а не литература. Грамматика не делает вас мудрым... но без нее вы не сможете связать и двух слов.
Для читателей, не знакомых с формализмом: не волнуйтесь. Базовый вопрос, на который отвечает теория категорий, обманчиво прост: когда можно соединять вещи друг с другом и что при этом происходит?. Это всё. Остальное - лишь строгость вокруг этого вопроса.
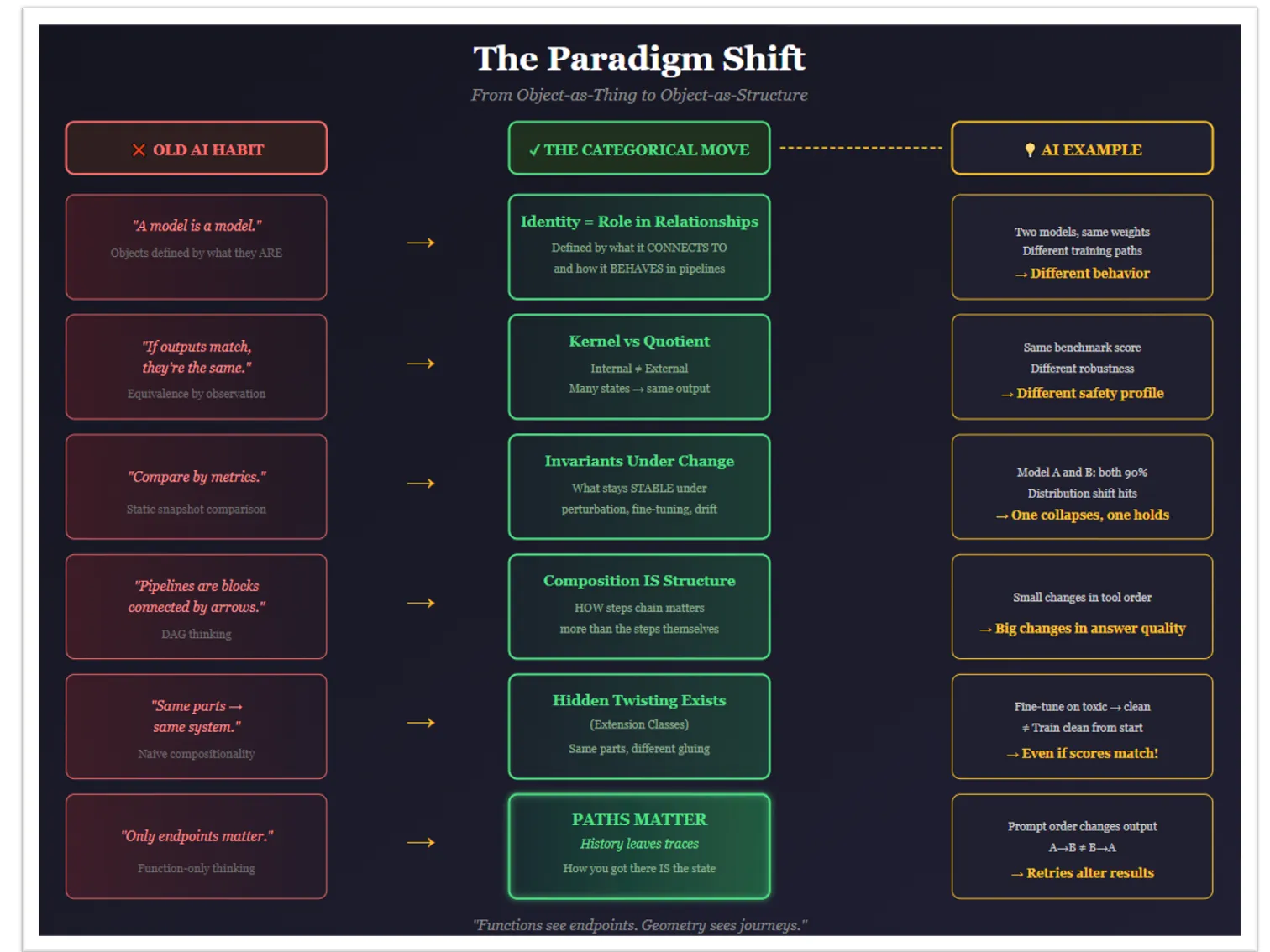
2. Первая ошибка: отношение к категориям как к простым функциям
Большинство работ по ИИ останавливаются на категории Set (Множества):
Объекты = множества
Морфизмы = тотальные функции
Композиция = композиция функций
Это уже является скрытым преступлением. Функции лишены памяти. Функция не знает: как вы пришли к входным данным, что было до этого и какую кривизну пространства вы пересекли. Она просто отображает вход в выход, как ячейка в вашей любимой таблице: f(x)=y. Ни контекста. Ни пути. Ни шрамов.
Но системы ИИ - это и есть накопленная история. Мы все знаем очевидное: каждый токен зависит от контекста. Каждое взаимодействие агента зависит от порядка этих взаимодействий. Каждая обученная модель несет в себе осадок пройденного пути обучения.
Поэтому, когда кто-то говорит, что «наша ИИ-система категориальна» (или, в узком смысле, функциональна), обычно имеется в виду: «мы просто соединяем кучу маппингов без сохранения состояния». Называть груду функций без состояния «категориальной глубиной» - это не наука. Это косплей.
3. Ядра (Kernels): часть реальности, которую не видит ваша архитектура
Здесь большинство дискуссий об ИИ заходят в тупик, потому что в них никогда не упоминаются ядра. Математически ядро - это просто: пространство различий, которые не создают никакой наблюдаемой разницы.
Ядро - это то, что меняется незаметно для окружающих, где «окружающие» - это ваш инструмент измерения. В ИИ это смертельно опасно: именно в ядрах прячутся монстры.
Потому что ИИ-системы полны направлений ядра: внутренних состояний, которые различаются; историй, которые расходятся; путей обучения, которые вращают систему... в то время как результат на выходе остается прежним.
Подумайте об этом. Две языковые модели, дообученные по совершенно разным траекториям: одна видела токсичный контент на ранних этапах и была «очищена», вторая изначально обучалась на чистых данных. В бенчмарках они набирают одинаковые баллы. Тот же результат. Но внутри? Совершенно разная геометрия. Разные режимы отказов, ждущие своего часа. Разные реакции на промпты, которые вы еще не тестировали.
Разница между ними живет в ядре вашей оценочной карты. Если ваша архитектура не может представить свое ядро, она не может знать, к чему она слепа. Это не философия. Это инженерия. И игнорирование этого - причина того, почему ИИ ломается в продакшене так, как никто не мог предсказать по бенчмаркам.
4. Фактор-множества (Quotients): когда вы решаете, что считать «одинаковым»
Теперь перейдем к эпистемологическому шагу. Имея ядро, мы формируем фактор-множество (quotient). Не путем удаления информации, а путем объявления различий неважными. Два состояния эквивалентны, если их разница лежит в ядре.
Фактор-множество - это реальность после акта забывания. ИИ-системы делают это постоянно:
Равенство токенов (разные представления Unicode → тот же токен)
Баллы бенчмарков (разные модели → тот же показатель точности)
Метрики успеха (разные пути рассуждения → правильный ответ)
Сходство эмбеддингов (разные смыслы → та же область вектора)
Разные внутренние миры. Тот же класс эквивалентности. И система не может отличить их друг от друга.
Вот неудобная правда: каждая метрика - это отображение в фактор-множество. Каждая оценка схлопывает огромное пространство внутренних состояний в тонкую линию цифр. Ядро этого отображения - всё, что ваша метрика не может различить, - это место, где прячутся все интересные сбои.
Когда ваш ИИ в продакшене уверенно галлюцинирует или когда «эквивалентные» модели ведут себя совершенно по-разному на крайних случаях - вы видите, как заявляют о себе направления ядра. Различия, которые вы объявили неважными, оказываются значимыми.
5. Ловушка «Ядро-Фактор»
Итак, у нас есть две операции:
Ядро: то, что ваша система не может видеть
Фактор: то, что ваша система отказывается различать
Вместе они образуют нашу ловушку для ИИ. Чтобы сделать системы управляемыми, мы агрессивно факторизуем их: объявляем огромные массивы состояний «эквивалентными» для наших целей. Бенчмарки, метрики, оценки - все это фактор-карты.
Но факторы не уничтожают ядро. Они его прячут. Состояния, которые вы схлопнули, все еще там; они развиваются и накапливают различия вдоль своих путей. Вы просто не видите их через выбранную линзу.
А потом в один прекрасный день что-то выплывает из ядра. Поведение, которое никто не предсказывал. Режим отказа, который не поймал ни один бенчмарк. Внезапный скачок способностей или поломка, которые на самом деле назревали месяцами в тех измерениях, к которым вы были слепы.
Ловушка «ядро-фактор» похожа на историю, где три персонажа стартуют в одном месте, а рассказчик сообщает вам только финал, но никогда не говорит, как они туда попали. Все они достигли 94,2%, заключает история. Но один шел чистым путем. Другой спиралью прошел через загрязнение. Третий в дюйме от обрыва. Финал выглядит одинаково. Пути - нет. А именно пути определяют, что произойдет в сиквеле.
Чтобы не гадать, как поведёт себя та или иная модель в ваших задачах, важно иметь под рукой удобный полигон для испытаний. Делегируйте часть рутинных задач вместе с BotHub!
Это удобный доступ к топовым нейросетям без VPN и с оплатой российскими картами.
По ссылке вы можете получить 100 000 бесплатных токенов для первых задач и приступить к работе прямо сейчас!
6. Пути, голономия и то, что функции не могут выразить
Теперь мы можем сформулировать основную проблему точно: композиция функций стирает пути. Реальность их помнит.
В плоских пространствах это не имеет значения. Все пути между двумя точками эквивалентны. Но пространства состояний ИИ не плоские. В них есть кривизна. А кривизна означает голономию: феномен, когда путь, который вы выбираете, меняет результат, даже если вы в итоге оказались в той же самой точке.
Представьте, что вы несете стрелку по поверхности планеты. Вы начинаете на Северном полюсе, стрелка указывает на Лондон. Идите в Лондон, держа стрелку параллельно (не вращая её). Затем идите по экватору в Токио. Вернитесь на Северный полюс. Вы вернулись в исходную точку. Но стрелка? Она указывает в другом направлении, чем в начале.
Ваш путь повернул её. Геометрия сферы вызвала трансформацию, которую чистая функция «от старта до финиша» не видит. Это и есть голономия. И в ИИ это происходит постоянно. Два пути обучения могут привести к одним и тем же весам модели. Тот же финиш. Но разная внутренняя геометрия. Разные режимы отказов.
Путь оставил следы, которые ваша функциональная архитектура не может представить. Если система не различает, как было достигнуто состояние, она не может рассуждать о явлениях, зависящих от траектории.
7. Иллюзия DAG: путаница диаграмм с динамикой
Современные системы ИИ рисуются как блок-схемы: направленные ациклические графы (DAG). Узлы - это модели, ребра - потоки данных. Это выглядит категориально. Можно прищуриться и увидеть объекты и стрелки.
Но это ничего не говорит о динамике. У DAG нет:
Понимания того, как вы его проходите
Накопленных ошибок вдоль пути
Памяти за пределами явно передаваемого состояния
Представления о собственном ядре
Конкретный пример: два ИИ-агента ведут переговоры. Агент А предлагает, Б критикует, А пересматривает. Теперь поменяйте порядок: пусть Б предлагает первым! Те же агенты. Та же композиция. Но результат другой. DAG говорит, что эти конвейеры эквивалентны. Реальность смеется в ответ. Порядок обхода вращает внутреннее состояние так, как DAG не видит, потому что у графов нет геометрии. Они плоские.
8. Преступление функционального программирования
Это не только проблема ИИ. Это проблема вычислительной культуры. Даже Haskell - предполагаемый «собор категориальной чистоты» - совершает то же преступление.
Haskell реализует категорию Hask (типы и функции), которая по сути является той же категорией Set с лучшим маркетингом. Монады, которые якобы управляют эффектами, этого не исправляют. Монада выстраивает вычисления в линейную цепь, но у этой цепи нет геометрии. Путь схлопывается в свою конечную точку.
То, что Haskell не может выразить:
Две последовательности операций, которые должны быть эквивалентны, но не являются ими (голономия)
Движение по вычислительной петле с возвращением в неожиданное место (кривизна)
Операции, зависящие от того, как вы прибыли в точку (зависимость от пути)
Вся махина функционального программирования построена на одной плоской категории. Монады, функторы - это просто перестановка мебели в комнате без окон.
9. Теория категорий уже решила это (никто не заметил)
В этом и заключается горькая ирония. Современная теория категорий (развитая с 1960-х) имеет мощный аппарат именно для этих феноменов:
Обогащенные категории: морфизмы несут структуру (стоимость, время, вероятность)
Высшие категории: морфизмы между морфизмами, фиксирующие трансформации трансформаций
Категории: башни морфизмов, кодирующие пути и петли
Пучки (Sheaves): локальное поведение, ограниченное глобальной согласованностью
Эти фреймворки осознают пути. Голономия и память живут там. Но почти ни одна архитектура ИИ их не использует. Сообщество ИИ все еще рисует плоские блок-схемы, называя их категориальными.
10. Что ломается на практике
Игнорирование структуры пути имеет последствия:
Ошибки накапливаются незаметно. В плоской композиции это шум. В искривленных пространствах они соединяются в траектории, которые уводят вас в неожиданные места.
Петли обратной связи непредсказуемы. Без геометрии нельзя предсказать, куда сойдутся эти петли - и сойдутся ли вообще.
Повторы не идемпотентны. Запуск того же взаимодействия агента дважды не должен иметь значения, но имеет, так как состояние эволюционировало по пути, который архитектура не отслеживает.
Автономные агенты превращаются в хаос. Возникают эмерджентные поведения — «колеи» и осцилляции, которые никто не проектировал, потому что никто не моделировал геометрию пространства их взаимодействия.
Вот почему слои оркестрации со временем «гниют». В итоге система превращается в путаницу неявных голономий, которые никто не может нанести на карту.
11. Как бы выглядел ИИ, учитывающий пути?
Подлинно осознающая пути архитектура ИИ должна:
Представлять пространства состояний как геометрические объекты (многообразия), где кривизна что-то значит
Явно отслеживать траектории: знать, как вы прибыли, а не только где вы
Моделировать ядра: знать, что архитектура не может различить, чтобы осознавать свои слепые зоны
Инструменты существуют: расслоения, параллельный перенос, характеристические классы. Теория категорий дает организационную основу, но нужны её обогащенные и высшие версии, а не фрагмент 1940-х годов.
12. Почему это произошло
Эта архитектурная слепота не случайна:
Машинное обучение выросло из статистики, а не из геометрии. Его метафоры - регрессия и оптимизация, которые живут в плоских пространствах.
Программная инженерия мыслит функциями. Категории множеств кажутся естественными, категории пространств - чуждыми.
Высшая теория категорий по-настоящему сложна. Проще налепить ярлык «категориальный» на DAG и опубликоваться.
Нет немедленной награды. Система с правильным отслеживанием путей не покажет лучшие результаты в сегодняшних бенчмарках. Выгоды проявятся в стабильности и интерпретируемости - вещах, которые не раздувают демо-показатели.
13. Обвинение
Давайте скажем прямо: проблема не в том, что теория категорий слишком абстрактна для ИИ. Проблема в том, что ИИ и компьютерные науки используют её искалеченный фрагмент: функции без путей, стрелки без памяти, ядра без признания.
Это не теория категорий. Это косплей. Это как утверждать, что используешь исчисление, отказываясь признавать производные. Мы заперли себя в вестибюле «Отеля Категория», игнорируя остальные этажи.
-категории, где пути, гомотопии и голономия становятся полноправными объектами... и где геометрия пространств состояний наконец обретает четкие очертания. Лифт исправен. Пентхаус сияет огнями. Но никто не поднимается наверх. И это не проблема инструментов. Это даже не проблема нехватки знаний. Это проблема культуры: композиция функций сработала, и восхождение прекратилось. Вестибюль кажется целым миром, если вы никогда не видели вид, открывающийся с высоты.14. Путь вперед
Математика уже решила эти проблемы. Что нужно сделать?
Исследователям ИИ: Изучите геометрию. Не только линейную алгебру, а настоящую дифференциальную геометрию. Поймите, что такое связность и кривизна.
Программистам: Признайте, что Haskell — не финал. Посмотрите на гомотопическую теорию типов (HoTT), где пути - это граждане первого класса.
Всем создателям ИИ: Когда ваша система ведет себя таинственно - это не шум. Это сигнал. Это геометрия, которую вы игнорируете, заявляет о себе.
Вопрос в том, повзрослеет ли ИИ, чтобы выучить реальную математику... или продолжит играть с плоскими диаграммами, удивляясь, почему ничего толком не работает.
Подводя итог...
Если архитектура не различает, как было достигнуто состояние, она не может по-настоящему рассуждать или адаптироваться. Если она не видит собственного ядра, она не знает, чего она не знает.
Теория категорий не была ошибочной. Она была неправильно использована. Пути все еще там, они изгибаются через ваши системы. Ядра все еще там, скрывая различия. Вы можете моделировать их или делать вид, что их нет. Но они будут иметь значение, признаете вы это или нет.
