100 лет спустя: заполненные пропуски в записях Рамануджана

Перевод поста Олега Маричева и Майкла Тротта "After 100 Years, Ramanujan Gap Filled".
Скачать файл, содержащий текст статьи, интерактивные модели и весь код, приведенный в статье, можно здесь.
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.

---

Сто лет назад Сриниваса Рамануджан и Г. Х. Харди начали знаменитую переписку о настолько поразительных вещах в математике, что Харди описал это как нечто едва возможное, чтобы в это поверить. Первого мая 1913-го года Рамануджан получил постоянную должность в Университете Кембриджа. Через пять лет и один день он стал научным сотрудником королевского общества, а его группа стала самой престижной на тот момент научной группой в мире. В 1919-ом году Рамануджан смертельно заболел во время длительного путешествия на пароходе Нагоя в Индию, которое проходило с 27-го февраля по 13-ое марта. Всё, что у него было — блокнот и ручка (да, никакой Mathematica в то время), и перед смертью он хотел оставить на бумаге свои уравнения. Он утверждал, что у него есть решения для целого ряда функций, однако ему хватало времени записать лишь несколько, прежде чем перейти к другим областям математики. Он записал следующее неполное уравнение и 14 других (см. ниже), из которых только три на данный момент решены.



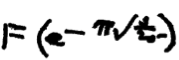
Он умирал несколько месяцев, вероятно, от печёночного амёбиаза. Его последний блокнот был отправлен Университетом Мадраса к Г. Х. Харди, который затем передал его математику Г. Н. Уотсону. В 1965-ом году, когда Уотсон умер, директор колледжа нашёл блокнот в его офисе, отбирая документы на уничтожение. Джордж Эндрюс заново открыл этот блокнот в 1976 году и, наконец, в 1987 году он был опубликован. Брюс Берндт и Эндрюс писали об утерянном Блокноте Рамануджана в серии книг (Часть 1, Часть 2, и Часть 3). Как сказал Берндт: «Открытие этого „утерянного блокнота“ вызвало бум в математическом мире такой же, какой могло бы вызвать открытие десятой симфонии Бетховена в мире музыкальном».

В своей книге, анализируя результаты Рамануджана, Берндт указывает на существование решения для , однако отмечает, что решение является не особо изящным, чтобы его в ней приводить. Как будет показано ниже, существует решение столь же изящное, сколь и остальные, найденные самим Рамануджаном.



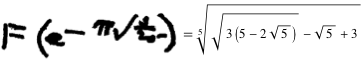
Что означает это уравнение? Начнём со сравнения арифметической и геометрической прогрессий.

Сумма первых n членов некоторой арифметической прогрессии: 1 + 2 + 3 + … + n.

Сумма первых n членов некоторой геометрической прогрессии: a¹ + a² + a³ + … + aⁿ.

Для каждого типа прогрессии мы можем предсказывать её поведение с помощью формулы частичной суммы, если свернуть приведенные выше выражения к их замкнутой форме.

Вот другая форма арифметической прогрессии, представленная в форме непрерывных дробей:



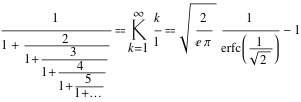
где символ соответствует функции ContinuedFractionK в Mathematica.

Аналогично, «геометрический» вариант непрерывных дробей известен как функция R Роджерса-Рамануджана. Она родственна функции S Роджерса-Рамануджана (Леонард Джеймс Роджерс публиковался вместе с Рамануджаном в 1919-ом году). В «утерянном блокноте» F(q) представляется как S(q).

R(q) — непрерывная дробь следующего вида:



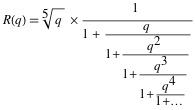
И аналогично для S(q). (Использование множителя делает формулы более «удобными»). Вот более формальные определения:





Эти функции связаны соотношением . Многие опубликованные работы упоминают S(q) = -R(-q), но это неверно из-за многолистности корня в комплексной области. Мы так же можем задать R и S через q-символы Похгаммера для существенного ускорения вычислений.





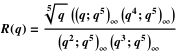
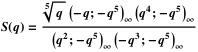
Вот иллюстрация поведения функции R в единичном кругеk на комплексной плоскости. Полученные значения могут быть комплексными, поэтому отображены действительная, мнимая части, аргумент и абсолютное значение (Im, Re, Arg и Abs) функции R(q). Сама единичная окружность является естественной границей аналитичности этой функции и содержит множество особенностей функции R(q). Как можно заметить, функции Роджерса-Рамануджана красивы не только из-за своих математических свойств, но и чисто визуально.



Функции R и S — две из небольшого количества именованных функций, связанных с непрерывными дробями. В последнее время мы собирали теоремы и формулы для функций R и S, включая незавершённые из «утерянного блокнота» Рамануджана. Последняя строчка эквивалентна .



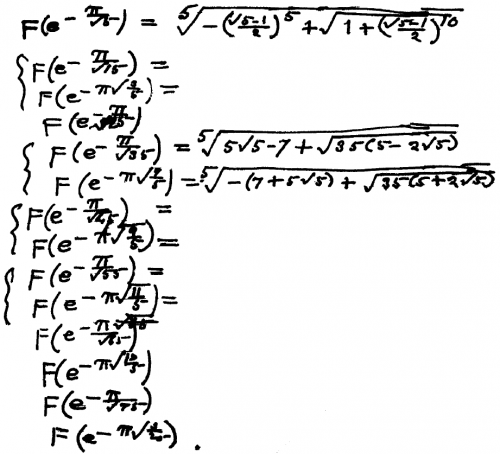
Многие из них были повторно найдены после Рамануджана. Все из них легко решаются в Mathematica. Приведём известные решения, начиная с тех, которые появились ранее, а так же те, которые Олег Маричев впервые реализовал в Mathematica.



Брюс Берндт отметил: «значение может быть определено через значение и известное уравнение, связывающее R(q⁵) с R(q). Не будем приводить здесь полученное значение, потому что оно не особо изящно.»

С Simplify, RootReduce и многими другими функциями Mathematica большие уравнения могут быть сведены к своей самой изящной форме. Рамануджан использовал мел и свой интеллект для упрощения получаемых результатов — громоздкие он стирал из своего списка, а изящные оставлял. Кажется вероятным, что Рамануджан на самом деле знал изящное решение, или по крайней мере способ найти его, но у него уже не оставалось времени, чтобы его записать. Вот метод, который мы использовали. Сперва следует получить численное значение в интересующей точке. Далее следует получить некоторую замкнутую алгебраическую форму для этого числа. Затем выразить полученное алгебраическое число через конструкцию из радикалов. Затем нужно проверить полученную форму численно с первоначальным значением с очень высокой точностью.















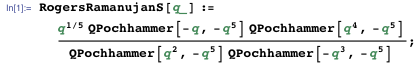
То есть мы проверяем, что численное значение предполагаемой формы такое же, как значение функции. Значения совпадают по крайней мере на первых 10,000 цифрах.





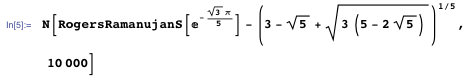
Поскольку они оба — алгебраические числа весьма изящного вида, то это — довольно убедительная проверка. И метод легко может быть обобщён для поиска многих неизвестных на данный момент значений S(q) и R(q).

Фактическое доказательство может быть реализовано через модульные уравнения (modular equations). Это модульное уравнение 5-го порядка для S:





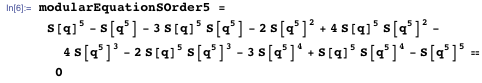
Мы используем ранее известное значение для S(q⁵) и решаем уравнение относительно S(q), чтобы получить значение .









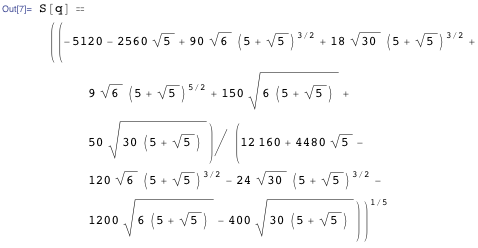
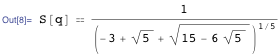
Избавившись от знаменателей, получаем приведённый ниже результат.





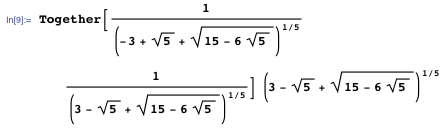
Уравнения Рамануджана близки по тематике к нашей недавней работе — добавлению множества различных знаний о непрерывных дробях в Wolfram|Alpha. В одном из следующих постов мы расскажем о новых возможностях, таких как ввод запроса о цепной дроби K (1, n, {n, 1, inf}).

Мы так же составили список сотен точных значений в интерактивной демонстрации “Ramanujan R and S”.



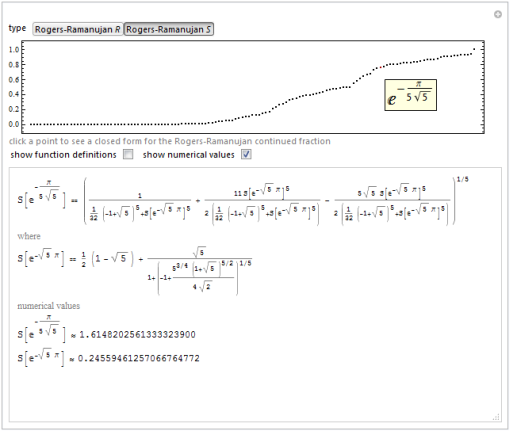
«Не особо изящно» — это то, чего никак нельзя сказать о работах Рамануджана. И мы рады были показать, насколько изящны его идеи.