Научно-популярное

Закон сохранения массы, изобретённый Ньютоном, утратил свою актуальность более полувека назад. С появлением квантовой физики стало понятно, что он является только частным и ограниченным случаем закона сохранения энергии и не всегда выполняется. При поступлении энергии в систему масса увеличивается и наоборот. Например, при нагревании утюга его масса увеличивается, а при термоядерных реакциях внутри Солнца масса получившегося гелия меньше, чем масса водорода. В случае с утюгом энергия поглощается, а в случае с Солнцем — выделяется.

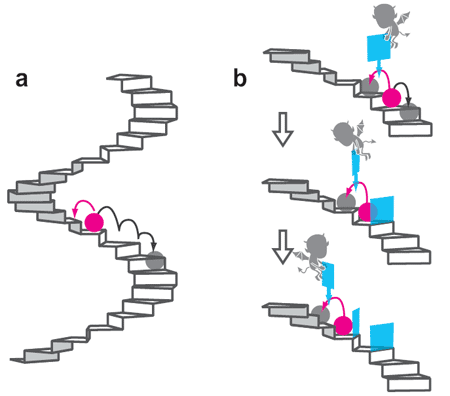
Необычные свойства графена (а именно то, что электроны в графене предположительно ведут себя как фермионы Дирака с нулевой эффективной массой — релятивистские частицы) дали богатую пищу для размышлений физикам-теоретикам. Например, группа физиков из Саудовской Аравии и Марокко выдвинула интересную теорию, в которой предположительные свойства графена объединены с теорией струн, а именно — с гипотезой о компактификации измерений.

Хорошая визуализация теории

Уникальные фотографии со съемочных площадок первых по времени съемок Звездных войн. Желающие могут пустить скупую мужскую слезу :)


Дарт Вейдер открывает свой секрет Люку, который висит над картонными коробками, накрытыми матрасами.


Фил Типпет и Джон Берг работают над анимацией трех шагающих роботов.

«Сколько-сколько рукопожатий?» Все ли мы знаем об устройстве сетей? И когда слабые связи оказываются сильными?

А действительно, что мы знаем о сетях? Очень многие уже в курсе, хотя при внимательном взгляде на этот предмет не все оказывается так просто. Почти все знают о странном факте «шести рукопожатий». Несмотря на то, что данное свойство сетей может быть доказано с математической (статистической) точностью, его бывает сложно осознать и всегда найдется множество сомневающихся. Смотри, например, интересные обсуждения этого предмета под знаком вопроса «миф или научная истина?» или в другом хабратопике  «Шесть рукопожатий сменяются тремя».

То, что сейчас известно в науке о реальном устройстве сетей, бывает не стыкуется с привычными представлениями о сетях. И поэтому попадаются на глаза забавные заблуждения, время от времени встречающиеся в форумах и блогах. Например, многие уверенны, что суть закона кроется в магическом числе, которое точно не известно (примерно 6 или 7 рукопожатий), но это число существует и, даже кажется, что оно (почти) фиксировано для любых сетей. Конечно же, само число не причем, оно может варьироваться для различных реальных сетей и довольно заметно. Более того, существуют примеры сетей, где правило шести рукопожатий вообще не работает и ниже здесь будет представлена подобная модель сети. На самом деле, все о чем говорит правило шести рукопожатий, — что мир тесен, и его размер в рукопожатиях почти всегда пренебрежимо мал, по сравнению с размером сети, подсчитанным по количеству узлов или связей. Как правило, все стихийно образуемые социальные сети все-таки выполняют правило шести (трех, дести и т.д. в разных сетях по разному) рукопожатий. Но вот в области транспортных сетей легко найти хорошо знакомые примеры сети, где это правило не выполняется. Это обычная сеть автодорог. Понятно, что мы считаем не рукопожатия, а перекрестки, повороты или населенные пункты, пройденные на пути из точки А в точку Б. Я не буду здесь подробно это доказывать, кажется, это не сложно понять просто открыв и проанализировав любую карту. Кстати, в сети авиасообщений правило «шести рукопожатий» (пересадок или транзитов) выполняется. В общем случае количество «рукопожатий» для каждой сети может зависеть от размера сети, статистического распределения связей между узлами, степени кластеризации и некоторых других не столь заметных факторов.

На днях произошел любопытный и местами смешной случай с одним из снимков аэрокосмического агентства NASA.



Если фотографию двух лун Сатурна (Дионы на фоне Титана), представленную выше, открыть в фотошопе и выкрутить контраст на максимум, то сразу вылезет вся «правда»:

Сегодня ее присудили двум ученым (Андрею Гейм и Константину Новосёлову ) из России за открытие графена.
Вообще над графеном работает коллаборация ученных из разных стран, но премию получили эти двое. Спустя всего несколько лет после открытия графена (это очень мало) наметились области его применения в реальной жизни:
На основе графена — пленки толщиной в 1 атом будут разработаны новые тачскрины. Если вам интересно узнать что такое графен более подробно и из из первых уст рекомендую видео лекцию Михаила Кацнельсона, ученого из Нидерландов, который работает в этой же коллаборации.

27 сентября 2010 года группа японских учёных под руководством Соити Тоябэ (Shoichi Toyabe) опубликовала результаты интересного эксперимента, который служит доказательством практической возможности превращения информации в энергию по принципу гипотетической машины Силарда. Под воздействием постоянного фидбек-контроля (меняя два электромагнитных поля) учёным удалось заставить частицу полистирола подниматься по спиральной лестнице, получая энергию от броуновского движения молекул в окружающем воздухе.


^{На иллюстрации из научной работы изображён демон Максвелла, который якобы помогает в эксперименте.}

Научная работа “Information heat engine: converting information to energy by feedback control” лежит в открытом доступе, можете ознакомиться с экспериментом.

Американский физик Александр Зибров вместе с группой помощников изобрёл лазерный компас принципиально новой конструкции, который способен максимально точно высвечивать направленность магнитного поля.

Метод Зиброва состоит в лазерной подсветке кристаллов рубидия-87, которые в определённых условиях (при температуре 45°C) создают решётку, зависимую от магнитного поля. С помощью лазера можно детектировать, как изменяется структура решётки при появлении магнитного поля, и эта информация даёт возможность точно установить силу и направленность поля.

Лазерный компас значительно превосходит все существующие компасы по простоте работы. Конечно, и сегодня существуют компасы, которые работают на лазерах и учитывают атомную решётку, но все они гораздо сложнее и требуют неких математических моделей.

Во время эксперимента компас Зиброва успешно детектировал магнитную индукцию от 0,1 гаусса до 200 гауссов. Это впечатляющие показатели. Авторы изобретения добавляют, что характеристики прибора можно регулировать, если изменять размер и температуру чипа.

Учёные из Имперского колледжа Лондона разработали теоретическую основу для первого эксперимента, который мог бы подтвердить справедливость теории струн. Предполагается, что теория струн — единственный способ формулирования так называемой единой теории, описывающей все известные фундаментальные взаимодействия в природе. Несмотря на математическую строгость и целостность теории, пока не найдены варианты экспериментального подтверждения теории струн.

Эксперимент британских учёных предполагает измерение степени запутанности четырёх кубитов. Дело в том, что последние научные работы обнаружили некоторую взаимосвязь между запутанностью кубитов в квантовой теории и чёрными дырами в теории струн. Если говорить конкретнее, то есть прямое соответствие между классификацией трёхкубитных взаимодействий и классификацией внешних чёрных дыр в теории супергравитации.

Всем кто следит за проектом Марс-500 наверняка будет интересно совершить виртуальную прогулку по марсианскому комплексу.

Исследователи из Университета штата Мичиган, факультетов электротехники и кинезиологии (это физиология движений), объединились для создания надежной и простой в эксплуатации системы, которая позволяет отслеживать собственную физическую активность. В наше время действительно сложно следить за тем, сколько ты работаешь за компьютером, понятно, сидя (ну или лежа), а сколько — работаешь физически (хотя бы зарядка). В общем, недолго думая, американцы создали беспроводную систему, действительно отслеживающую физическую активность человека. Для этого нужно закрепить на теле три небольших беспроводных сенсора, на определенных частях тела (запястье, плечо, колено). Вот и все, подготовка к работе системы завершено. После этого все данные, считываемые сенсорами, будут поступать по беспроводной сети на оснащенные специальным ПО компьютерам.

В продолжение столь тепло принятого моего прошлого поста про Луну, не могу не продолжить тему и представляю следующий материал о Меркурии:

• Меркурий — самая близкая к Солнцу планета.
• Среднее расстояние до Солнца — 57,91 млн км (0,387 а.е.), т.е. втрое ближе чем Земля.
• Меркурий получает в 7 раз больше солнечной энергии, чем Земля.
• Меркурианские солнечные сутки длятся два меркурианских года (сутки длиннее года из-за необычного соотношения орбитальной скорости и скорости вращения вокруг своей оси).
• Орбитальная скорость Меркурия самая высокая среди планет — 47,87 км/с (1,64 Земной).
• Объём — 6,08272·10¹⁰ км³, что составляет 0,056 Земных.
• Радиус составляет всего 2439,7 км, что даже меньше радиусов спутника Юпитера Ганимеда и спутника Сатурна Титана.
• Таким образом, Меркурий — самая маленькая планета в Солнечной системе (да да, Плутон хоть и меньше, но уже не считается планетой).
• Масса Меркурия — 3,3022·10²³ кг (0,055 Земных).
• Ускорение свободного падения — 3,7 м/с² или 0,377 g.

Интересности

Несмотря на то, что ближайшими к Земной орбитами являются орбиты Марса и Венеры, именно Меркурий является большую часть времени ближайшей к Земле планетой.

Меркурий имеет предельно разреженную атмосферу, давление которой в 5·10¹¹ раз меньше давления земной атмосферы. В таких условиях атомы чаще сталкиваются с поверхностью планеты, чем друг с другом.

Скажу кратко — разработка впечатляет.

Астрономом Тед Бауэлл (Ted Bowell) из Обсерватории Лоуэлла (Lowell Observatory) и его коллеги использовали набор данных "astorb.dat"(The Asteroid Orbital Elements Database), содержащую в себе информацию о всех известных человечеству астероидах, создали компьютерную модель нашей солнечной системы с визуализацией всех ближайших астероидов.

Эта поистине впечатляющая работа стала доступна для просмотра всем желающим.

В самом начале на анимации показаны местоположения всех астероидов, известных на момент начала 1980 года, затем, в хронологическом порядке по мере их обнаружения, на изображение добавляются новые астероиды. Эта анимация является ярким и наглядным примером развития современной астрономии и истории изучения Солнечной системы и использует данные обсерваторий и астрономов-любителей со всего мира.

Long Bets — это сайт, где любой желающий может сделать ставку или долгосрочный прогноз, какого-либо события, имеющего научный или социальный интерес.
-----------------------------------------------------------------------------
Минимальная сумма ставки — 200$
Минимальный срок — 2 года
-----------------------------------------------------------------------------
Ниже предлагаю список из 10 наиболее интересных пари, которые активны на данный момент:

1. До 2029 никакой компьютер или искусственный интеллект не пройдет Тест Тьюринга.

2. К 2012 Wall Street Journal и New York Times будут именовать Россию, как «мировой лидер в разработке программного обеспечения».

Статья публикуется по просьбе моего товарища kokoff.



После прочтения статей о человеческом мозге долго не получалось написать о задуманном, но вот наконец таки. Заметил часто встречающееся определение, которое вынес в заголовок. Меня самого очень сильно интересует это сторона психологии человека. Считаю, что порой она играет излишне сильную роль в жизни некоторых людей. Что греха тоить? У меня самого, есть парочка стереотипов, которые раздражают и с ними веду активную борьбу. Всем тем содержанием, что под катом, я хочу подробно раскрыть суть понятия и некоторые проблемы с ним связанные. Для изложения использовал литературу, интернет и личный жизненный опыт. Статья содержательная — надеюсь будет интересно и полезно почитать.

Давно на Хабре не было постов на космическую тематику. Тем не менее, космические статьи зачастую достаточно интересны хабрасообществу. Слово MESSENGER в заголовке возможно поначалу воспримется как «Instant Messenger», а статья – как очередная новость о детище от Майкрософт. Но речь пойдет немного о другом.

Вниманию читателей предлагается небольшая статья о космическом проекте MESSENGER.
MESSENGER – научное исследование планеты Меркурий путем запуска к ней космического корабля.
Имя миссии MESSENGER составлено из английских фраз:
MErcury Surface (Поверхность Меркурия)
Space ENvironment (Космическое пространство)
GEochemistry (Геохимия)
Ranging (Классификация).
Сам же Меркурий, кстати, назван в честь мифического посланника (англ. messenger) богов.

Под катом сведения о проекте и любопытные фотографии.

Меня всегда интересовали новинки в мире технологий, в частности, технологий информационных. Несколько дней назад, 10-го августа, прочитал на страничке ФИАН интересную информацию о спинтронных структурах, которые позволяют создать новейшие энергонезависимые магниторезистивные носители информации. Суть метода — использование не только заряда электрона, но и спина электрона, которым, как известно, можно управлять посредством магнитного поля. В результате создания новейших наноструктур «ферромагнетик — изолятор — ферромагнетик» на основе FeSix, MgO и FeOy возможна и реализация реальных носителей информации, которые работают на указанном принципе. В общем-то, дело нужное, новые носители информации нужны, как никогда. Но интересно также и другое — сегодня нашел публикацию (примерно того же времени, что и российская) на страничках сайта Ohio State University, где слово в слово повторяется то, что уже было прочитано мной на сайте ФИАН. Суть не в самой идее, а в том, что ученые и первой, и второй организации создали аналогичные модели спинтронной системы.

Большой адронный коллайдер (LHC) уже начал свою работу. Его запуск вызвал значительный интерес и сопровождался большим количеством разнообразных и, порой, антинаучных слухов и спекуляций.

Одной из важных целей работы LHC является проверка суперсимметричных моделей. Суперсимметрия как раз является областью моей научной деятельности, и я решил в научно-популярной форме попытаться рассказать, что же это такое.

Я остановлюсь в этой статье на современных теориях физики элементарных частиц, на некоторых идеях и следствиях этих теорий. Среди рассмотренных тем следующие:

• Стандартная модель фундаментальных взаимодействий (описывает практически все экспериментальные данные в физике элементарных частиц),
  
• ее достоинства и недостатки,
  
• идея суперсимметрии,
  
• решение многих проблем Стандартной модели при ее суперсимметричном обобщении,
  
• некоторые особенности минимальной суперсимметричной Стандартной модели (МССМ),
  
• экспериментальный статус суперсимметрии.
  

Я постарался вести рассказ максимально популярно, поэтому пришлось отказаться от математической строгости. Однако кое-где предполагается, что хабралюди, все-таки, еще помнят школьную математику и физику. Без этого было бы затруднительно, если вообще возможно, изложить часть понятий и идей.

Существует множество алгоритмов, которые собирают кубик Рубика — более или менее эффективно. Те из них, которые может выучить и применять средний смертный, обычно требуют более 40 ходов. Алгоритмом бога называют алгоритм, использующий для сборки любой начальной конфигурации минимальное количество ходов (термин связан с концепцией всеведения и применяется также для ряда других механических и логических задач). Число бога, соответственно, определяют как количество ходов, требующееся этому алгоритму в худшем случае. Так вот, для кубика Рубика это число равно 20.

Немного истории

Сам кубик был придуман в 1974 году. Теоретические исследования кубика сосредотачивались на оценке нижней и верхней границ максимального количества ходов для решения кубика.