Топологическая сортировка (Topological sort) — один из основных алгоритмов на графах, который применяется для решения множества более сложных задач.
Задача топологической сортировки графа состоит в следующем: указать такой линейный порядок на его вершинах, чтобы любое ребро вело от вершины с меньшим номером к вершине с большим номером. Очевидно, что если в графе есть циклы, то такого порядка не существует.
Ориентированной сетью (или просто сетью) называют бесконтурный ориентированный граф. В задачах подобного плана рассматриваются только конечные сети.
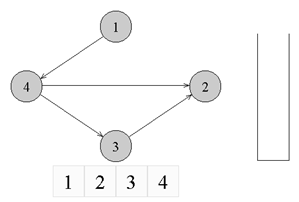
Из рисунка видно, что граф не отсортирован, так как ребро из вершины с номером 4 ведет в вершину с меньшим номером (2).
Существует несколько способов топологической сортировки — из наиболее известных:
Поиск в глубину или обход в глубину (англ. Depth-first search, сокращенно DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Подробнее о поиске в глубину можно почитать в статье на Хабре.
Запускаем обход в глубину, и когда вершина обработана, заносим ее в стек. По окончании обхода в глубину вершины достаются из стека. Новые номера присваиваются в порядке вытаскивания из стека.
Цвет: во время обхода в глубину используется 3 цвета. Изначально все вершины белые. Когда вершина обнаружена, красим ее в серый цвет. Когда просмотрен список всех смежных с ней вершин, красим ее в черный цвет.
Думаю будет проще рассмотреть данный алгоритм на примере:

↑ Имеем бесконтурный ориентированный граф. Изначально все вершины белые, а стек пуст. Начнем обход в глубину с вершины номер 1.
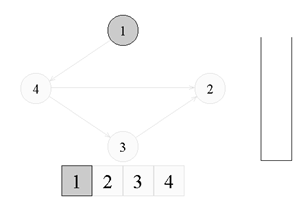
↑ Переходим к вершине номер 1. Красим ее в серый цвет.

↑ Существует ребро из вершины номер 1 в вершину номер 4. Переходим к вершине номер 4 и красим ее в серый цвет.

↑ Существует ребро из вершины номер 4 в вершину номер 2. Переходим к вершине номер 2 и красим ее в серый цвет.
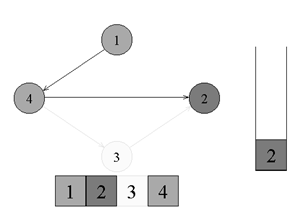
↑ Из вершины номер 2 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 2 в черный цвет и кладем ее в стек.
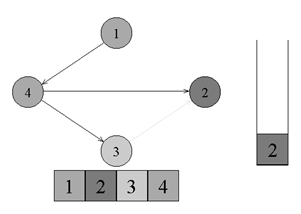
↑ Существует ребро из вершины номер 4 в вершину номер 3. Переходим к вершине номер 3 и красим ее в серый цвет.
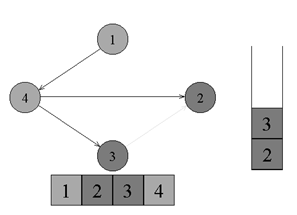
↑ Из вершины номер 3 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 3 в черный цвет и кладем ее в стек.

↑ Из вершины номер 4 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 1. Красим вершину номер 4 в черный цвет и кладем ее в стек.
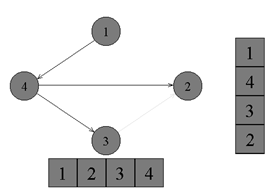
↑ Из вершины номер 1 нет рёбер, идущих не в черные вершины. Красим её в черный цвет и кладем в стек. Обход точек закончен.

↑ По очереди достаем все вершины из стека и присваиваем им номера 1, 2, 3, 4 соответсвенно. Алгоритм топологической сортировки завершен. Граф отсортирован.
Топологическая сортировка применяется в самых разных ситуациях, например при распараллеливании алгоритмов, когда по некоторому описанию алгоритма нужно составить граф зависимостей его операций и, отсортировав его топологически, определить, какие из операций являются независимыми и могут выполняться параллельно (одновременно). Примером использования топологической сортировки может служить создание карты сайта, где имеет место древовидная система разделов. (если интересно — to google)
Что касается реализации — здесь Вы можете найти 22 строчки кода, реализующих данный алгоритм (все тщательно закомментировано)
Задача топологической сортировки графа состоит в следующем: указать такой линейный порядок на его вершинах, чтобы любое ребро вело от вершины с меньшим номером к вершине с большим номером. Очевидно, что если в графе есть циклы, то такого порядка не существует.
Ориентированной сетью (или просто сетью) называют бесконтурный ориентированный граф. В задачах подобного плана рассматриваются только конечные сети.

↑ Пример ориентированного неотсортированного графа, к которому применима топологическая сортировка
Из рисунка видно, что граф не отсортирован, так как ребро из вершины с номером 4 ведет в вершину с меньшим номером (2).
Существует несколько способов топологической сортировки — из наиболее известных:
- Алгоритм Демукрона
- Метод сортировки для представления графа в виде нескольких уровней
- Метод топологической сортировки с помощью обхода в глубину
Суть алгоритма
Поиск в глубину или обход в глубину (англ. Depth-first search, сокращенно DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Подробнее о поиске в глубину можно почитать в статье на Хабре.
Запускаем обход в глубину, и когда вершина обработана, заносим ее в стек. По окончании обхода в глубину вершины достаются из стека. Новые номера присваиваются в порядке вытаскивания из стека.
Цвет: во время обхода в глубину используется 3 цвета. Изначально все вершины белые. Когда вершина обнаружена, красим ее в серый цвет. Когда просмотрен список всех смежных с ней вершин, красим ее в черный цвет.
Думаю будет проще рассмотреть данный алгоритм на примере:

↑ Имеем бесконтурный ориентированный граф. Изначально все вершины белые, а стек пуст. Начнем обход в глубину с вершины номер 1.

↑ Переходим к вершине номер 1. Красим ее в серый цвет.

↑ Существует ребро из вершины номер 1 в вершину номер 4. Переходим к вершине номер 4 и красим ее в серый цвет.

↑ Существует ребро из вершины номер 4 в вершину номер 2. Переходим к вершине номер 2 и красим ее в серый цвет.

↑ Из вершины номер 2 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 2 в черный цвет и кладем ее в стек.

↑ Существует ребро из вершины номер 4 в вершину номер 3. Переходим к вершине номер 3 и красим ее в серый цвет.

↑ Из вершины номер 3 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 3 в черный цвет и кладем ее в стек.

↑ Из вершины номер 4 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 1. Красим вершину номер 4 в черный цвет и кладем ее в стек.

↑ Из вершины номер 1 нет рёбер, идущих не в черные вершины. Красим её в черный цвет и кладем в стек. Обход точек закончен.

↑ По очереди достаем все вершины из стека и присваиваем им номера 1, 2, 3, 4 соответсвенно. Алгоритм топологической сортировки завершен. Граф отсортирован.
Применение
Топологическая сортировка применяется в самых разных ситуациях, например при распараллеливании алгоритмов, когда по некоторому описанию алгоритма нужно составить граф зависимостей его операций и, отсортировав его топологически, определить, какие из операций являются независимыми и могут выполняться параллельно (одновременно). Примером использования топологической сортировки может служить создание карты сайта, где имеет место древовидная система разделов. (если интересно — to google)
Что касается реализации — здесь Вы можете найти 22 строчки кода, реализующих данный алгоритм (все тщательно закомментировано)
