Недавно прочитал пост из «Дополненной реальности», в котором упоминается Фильтр Калмана в сравнении с более простым «альфа-бета» фильтром. Давно собирался сочинить нечто вроде сниппета по составлению ФК, и вот думаю самое время. В статье я вам расскажу как на практике можно составить расширенный ФК не особо утруждая себя высоконаучными размышлениями и глубокими теоретическими изысканиями.Основные понятия
- Уравнение «вход-выход» — это дифференциальное уравнение (например, составленное по уравнениям Лагранжа второго рода), у которого с левой стороны от знака равенства находятся слагаемые, зависящие от переменной выхода (обобщенные координаты собственного движения системы), а с правой — слагаемые с входной переменной или свободные члены. Для простоты можно привести следующий пример: для маятника в левой части уравнения «вход-выход» будут стоять слагаемые с углом отклонения груза от положения покоя, а в правой — слагаемые с силой тяжести и другими внешними силами. Как получаются такие уравнения я описывать не буду — нет необходимости усложнять публикацию бесполезными теоретическими выкладками. Ниже покажу, что обойтись можно удобными для практики методами.
- Передаточная функция (ПФ) — отношение выхода ко входу, вернее выходной переменной ко входной. По правилу пропорции, после выноса
мозгапеременных за скобки, передаточная функция будет равна отношению левой части, записанной в операторной форме, к правой. - Операторная форма записи — в ней записывается уравнение «вход-выход» после замены вида: s = d/dt и x(t) -> x(s). В результате уравнение вида:
a1*x''+a2*x'+a3*x = b1*u'+b2*u,
преобразуется к виду:
(a1*s^2+a2*s+a3)*x(s) = (b1*s+b2)*u(s).
При этом передаточная функция будет иметь вид:
W(s) = x(s)/u(s) = (b1*s+b2)/(a1*s^2+a2*s+a3)
Задача
В качестве приложения для ФК возьмем задачу обработки информации блока датчиков (см. [1]). Мы имеем четыре единицы двухосевых микромеханических акселерометров (ММА). Всего 8 измерительных каналов, для каждого из которых можно составить отдельное уравнение типа «вход-выход». Тут следует заметить, что некоторые из производителей датчиков (к примеру, Analog Devices) предоставляют приближенную линеаризованную (это важно в нашем случае) математическую модель. При работе над дипломом я получил от коллег модель для MatLab. Но даже, если производитель
Таким образом, мы сами можем составить нужную нам модель датчиков. И таким путем мы убиваем сразу двух зайцев: составляем простую линеаризованную модель и вводим фильтрацию шумов уже на самом низком уровне. Про простоту модели нужно заметить, что при использовании уравнения, точно описывающего динамику датчика, мы будем вынуждены составлять матрицы фильтра Калмана из чисел, порядки которых сильно различаются. В модели «от производителя» для упомянутых акселерометров отношение максимального коэффициента к минимальному — порядка 1e+10. Это приводит к жестоко низкой обусловленности вычислений, т.е. малая погрешность в задании значения коэффициента может привести к очень большой вычислительной погрешности. Сужая полосу пропускания, заложенную в математическую модель, мы по сути увеличиваем стабильность вычислений.
Так как составить эту самую модель? Да очень просто. Воспользовавшись пакетами MatLab или Octave и задавшись нужной нам полосой пропускания (ФНЧ, ФВЧ или полосового фильтра), методом тыка или с помощью плагинов в пакетах синтезируем ПФ. Тут нужно заметить, что в пакет MatLab входит визуальное средство синтеза дискретного фильтра. В Octave пока я аналога не нашел. В обоих пакетах можно построить графики АЧХ и ФЧХ, на которых нужно обратить внимание на частоту (или частоты) среза, а также на колебания графика АЧХ в и вне полосы пропускания. В общем, шаманим с коэффициентами передаточной функции до тех пор, пока графики АЧХ и ФЧХ нас не удовлетворят. Я же для себя уже наметил другой, более
Математическая модель
И так для простоты условимся, что имеется уравнение в операторной форме:
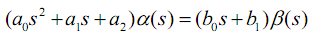
Это одно из самых распространенных уравнений динамического звена второго порядка. В этом уравнении а2 — играет роль коэффициента жесткости пружины (сила жесткости прямо пропорциональна расстоянию положения чувствительного элемента от положения покоя); а1 — коэффициент демпфирования (сила, пропорциональная скорости движения; вспомните о мёде — медленно двигать в нем ложку легче, чем быстро); а0 — характеризует инерцию. В коэффициенты справа от знака равенства вкладывается несколько иной смысл. Эти коэффициенты характеризуют эффективность воздействия по разным порядкам производных. Тут важно понимать, что требование физической реализуемости ограничивает максимальный порядок производной справа максимальным порядком производной левой части.
Получив в распоряжение такое уравнение мы можем начинать подготовку к составлению фильтра Калмана. Для этого нам сначала нужно преобразовать уравнение «вход-выход» к модели «пространства состояний». Это делается с помощью преобразования к «форме Коши».
Для начала следует преобразовать к форме пропорций и ввести новую (фиктивную) переменную:
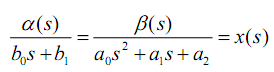
В результате получим систему уравнений:
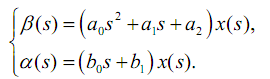
В этой системе первое уравнение — уравнение динамического процесса, а второе — уравнение наблюдения.
Приведем первое уравнение к форме Коши (к системе дифференциальных уравнений первого порядка) заменой x1 = x:
Для удобства записи замен в этой системе было произведено обратное преобразование
Лапласа (переход от операторной формы к дифференциальной). В результате мы разбили
исходное уравнение на два уравнения первого порядка. Введенные переменные х1 и х2 называются «переменными состояния» или «фазовыми координатами». Полученная система оперирует «непрерывным» временем. Мы ее составляли по исходным дифференциальным уравнениям. Но нам нужно построить разностный алгоритм (алгоритм в дискретном времени) для вычисления значения фазовых координат рекуррентным способом в ЭВМ. Поэтому перед использованием в фильтре Калмана эту систему нужно будет «дискретизовать». Но об этом позже.
Сейчас нам нужно составить уравнение наблюдения для введенных фазовых координат. С учетом
введенных замен и в дифференциальной форме получим:
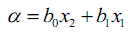
Остается переписать полученные уравнения в векторно-матричной форме, предварительно расставив слагаемые в соответствии с индексами фазовых координат:
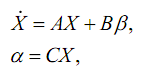
В этом уравнении
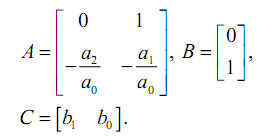
Для дискретизации этих уравнений нужно использовать следующие выражения:
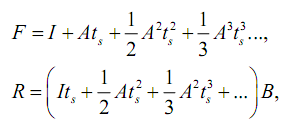
где I — единичная матрица, F и R — искомые дискретизированные матрицы модели пространства состояний (разностных уравнений), ts — период квантования.
Период квантования – это ключевой элемент в дискретизации. Чем он меньше, тем точнее
повторяет дискретная модель поведение модели с непрерывным временем. К тому же, при
слишком больших значениях ts из-за вычислительных погрешностей дискретная модель станет
неустойчивой. Если объект не является высоко динамичным (например, фильтр низких частот с
полосой пропускания до 10 Гц), то период квантования можно выбрать достаточно большим. Для
упомянутого ФНЧ период квантования можно выбрать с большим запасом равным 0.01 сек.
Итак, мы получили дискретную модель вида:
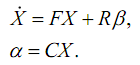
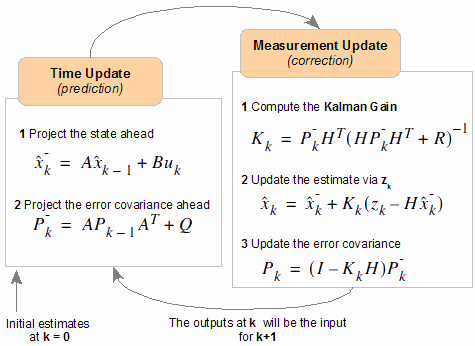
Теперь все готово для составления модели ФК. Мы должны просто выстроить по диагонали полученные для каждого измерительного канала матрицы F, R, и С. Для 8 измерительных каналов, для каждого из которых составлена дискретная собственная матрица F с размерами 2х2 мы получим собственную матрицу A фильтра Калмана (см. изображение в начале публикации) с размерами 16х16. Также поступаем с вектором-столбцом R: 2х1 * 8 каналов = 16х8 — матрица B в модели ФК. Из векторов-строк C составляется матрица H фильтра Калмана (8х16).
Готово! Дальше нужно это все запрограммировать. Лично я предпочитаю для этого использовать Ruby + NArray — прототипировать с этой связкой одно удовольствие, но это мое личное мнение… кому как. Только учтите, что в лоб программировать эти уравнения не стоит — полученные матрицы сильно разрежены нулями. Если подумать, то все матричные выражения можно разбить на блочные операции. Оптимизировать здесь много чего нужно на стадии реализации.
Заключение
Извините за некоторую путаницу в обозначениях. Формулы дергались из разных трудов. Постараюсь кратко разъяснить что есть что в уравнениях ФК на изображении в начале поста.
Первое, что может броситься в глаза — матрицы P, Q, R, K. Это, соответственно, матрица ковариаций ошибок оценивания (ошибок решения задачи ФК), матрицы ковариаций шумов динамического процесса и измерительных шумов, а также матрица коэффициентов усиления фильтра Калмана. Векторы «х» и «z» — это фазовый вектор ФК (имитация фазового вектора блока датчиков внутри модели ФК) и вектор выходных сигналов реальных датчиков (по сути это канал поступления информации извне в ФК). Из представленной диаграммы легко понять принцип работы ФК.
Вроде ничего сложного. Однако в работе ФК существует ряд важных нюансов. Так ФК разработан как алгоритм, дающий наименьшую среднеквадратическую ошибку при соблюдении нескольких условий (гипотез). Первая — шумы являются белыми (равномерная спектральная характеристика) с гауссовым распределением случайных величин. Но на практике эта гипотеза не выполняется, т.к. трудно найти источник шумов с такими идеальными параметрами. К тому же сами измерительные системы имеют конечные полосы пропускания. В этом случае в фазовый вектор ФК нужно включить еще и переменные для шумовых процессов. Используется искусственный подход: считается, что у нас есть источник белого шума, сигнал от которого проходит через фильтр. Таким образом в модель ФК добавляется модель еще двух динамических объектов — фильтров, которые преобразуют пару белых шумовых процессов в цветные шум динамического процесса и измерительный шум.
Вторая гипотеза — некоррелированность шумов разных измерительных каналов. Она также выполняется редко и опять же есть искусственные методы обойти это ограничение. Все эти методы приводят к увеличению размерности ФК => увеличивают вычислительную нагрузку.
Тонкости работы ФК усложняют жизнь
Список литературы
- Неортогональная БИНС для малых БПЛА
- habrahabr.ru/blogs/augmented_reality/118192
- Браммер К., Зиффлинг Г. Фильтр Калмана-Бьюси. Пер. с нем. – М.: Наука. Главная
редакция физико-математической литературы. 1982. - Сизиков В.С. Устойчивые методы обработки результатов измерений. Учебное пособие.
– СПб.: «СпецЛит», 1999. – 240 с. - Greg Welch, Gary Bishop. An Introduction to the Kalman Filter. TR 95-041, Department of
Computer Science, University of North Carolina at Chapel Hill. April 5, 2004.
