Данная статья рассказывает не только о наиболее распространённых фильтрах обработки изображений, но в понятной форме описывает алгоритмы их работы. Статья ориентирована, прежде всего, на программистов, занимающихся обработкой изображений.
Фильтров использующих матрицу свёртки много, ниже будут описаны основные из них.
Матрица свёртки – это матрица коэффициентов, которая «умножается» на значение пикселей изображения для получения требуемого результата.
Ниже представлено применение матрицы свёртки:
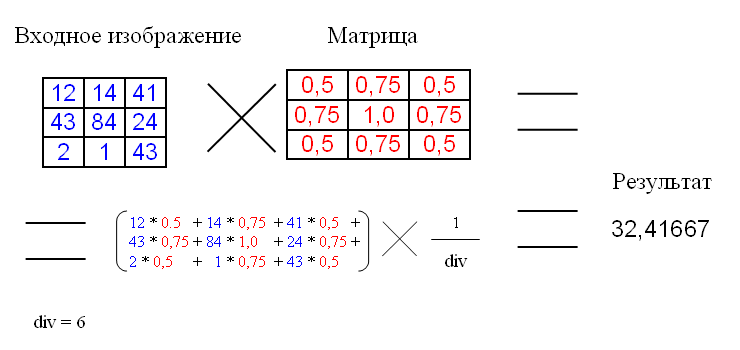
div – это коэффициент нормирования, для того чтобы средняя интенсивность оставалась не изменой.
В примере матрица имеет размер 3x3, хотя размер может быть и больше.
Наиболее часто используемым фильтром, основанным на матрице свёртки, является фильтр размытия.
Обычно матрица заполняется по нормальному (гауссовому закону). Ниже приведена матрица размытия 5x5 заполненная по закону Гауссовского распределения.
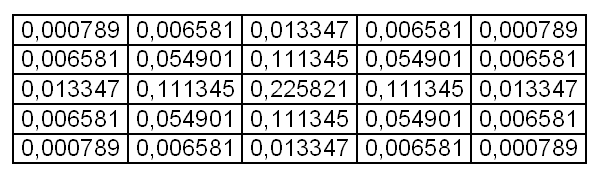
Коэффициенты уже являются нормированными, так что div для этой матрицы равен одному.
От размера матрицы зависит сила размытия.

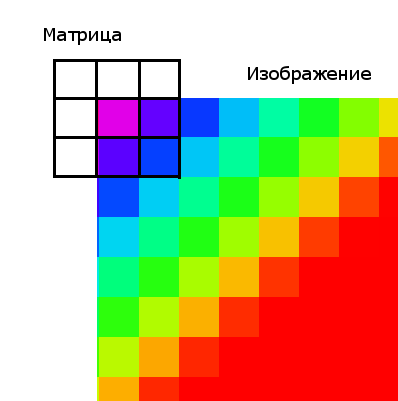
Стоит упомянуть о граничных условиях (эта проблема актуальна для всех матричных фильтров). У верхнего левого пикселя не существует «соседа» с права от него, следовательно, нам не на что умножать коэффициент матрицы.
Существует 2 решения этой проблемы:
1. Применение фильтра, только к «окну» изображения, которое имеет координаты левого верхнего угла [kernelSize / 2, kernelSize / 2], а для правого нижнего [width — kernelSize / 2, height — kernelSize / 2]. kernelSize – размер матрицы; width, height – размер изображения.
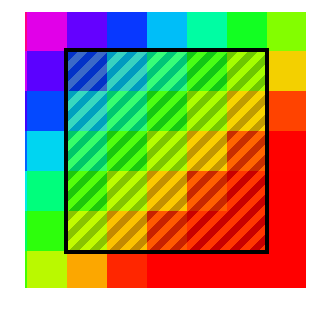
Это не лучший способ, так как фильтр не применяется ко всему изображению. Качество при этом довольно сильно страдает, если размер фильтра велик.
2. Второй метод (дополнение) требует создания промежуточного изображения. Идея в том, чтобы создавать временное изображение с размерами (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). В центр изображения копируется входная картинка, а края заполняются крайними пикселями изображения. Размытие применяется к промежуточному буферу, а потом из него извлекается результат.
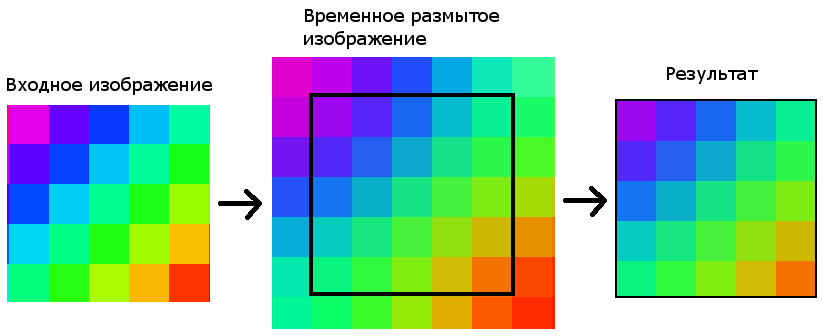
Данный метод не имеет недостатков в качестве, но необходимо производить лишние вычисления.
Фильтр размытия по Гауссу имеет сложность O(hi * wi * n *n), где hi, wi – размеры изображения, n – размер матрицы (ядра фильтра). Данный алгоритм можно оптимизировать с приемлемым качеством.
Квадратное ядро (матрицу) можно заменить двумя одномерными: горизонтальным и вертикальным. Для размера ядра 5 они будут иметь вид:

Фильтр применяется в 2 прохода: сначала горизонтальный, а потом к результату вертикальный (или на оборот).
Сложность данного алгоритма будет O(hi * wi * n) + O(hi * wi * n) = 2 * O(hi * wi * n), что для размера ядра больше двух, быстрее, чем традиционный метод с квадратной матрицей.
Для улучшения четкости необходимо использовать следующую матрицу:
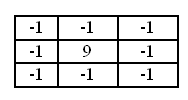
Эта матрица увеличивает разницу значений на границах. Div для этой матрицы равен 1.

В программе GIMP есть фильтр «Матрица свёртки», который упрощает поиск необходимого Вам матричного преобразования.
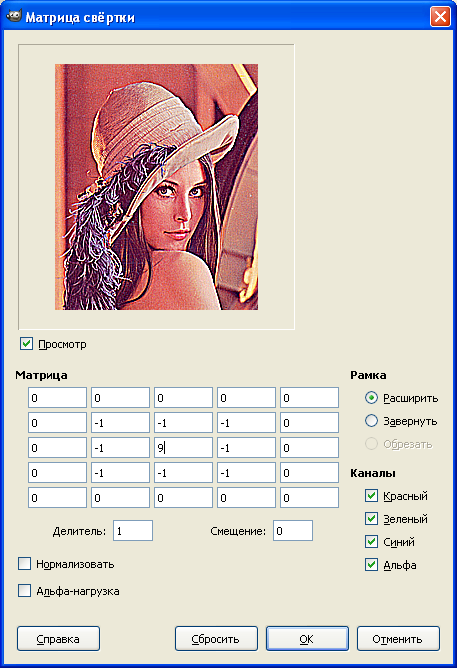
Более подробную информацию о фильтрах основанных на матрице свёртки вы можете найти в статье «Графические фильтры на основе матрицы скручивания».
Медианный фильтр обычно используется для уменьшения шума или «сглаживания» изображения.

Фильтр работает с матрицами различного размера, но в отличие от матрицы свёртки, размер матрицы влияет только на количество рассматриваемых пикселей.
Алгоритм медианного фильтра следующий:
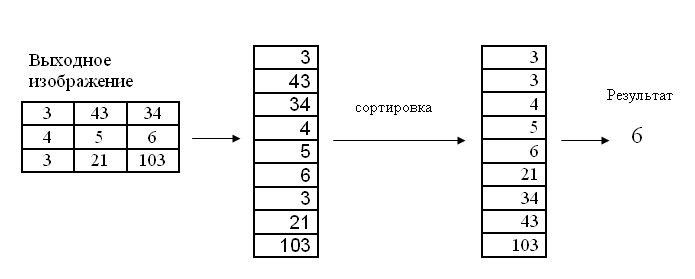
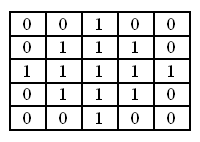
Для текущего пикселя, пиксели, которые «попадают» в матрицу, сортируются, и выбирается средние значение из отсортированного массива. Это значение и является выходным для текущего пикселя.
Ниже представлена работа медианного фильтра для размера ядра равного трём.
Фильтры наращивание и эрозия служат для получения морфологического расширения или сужения соответственно. Проще говоря, для изображений это значит выбор пикселя с максимальной или минимальной интенсивностью из окрестности.

В результате наращивания происходит увеличение ярких объектов, а эрозии – увеличение тёмных объектов.
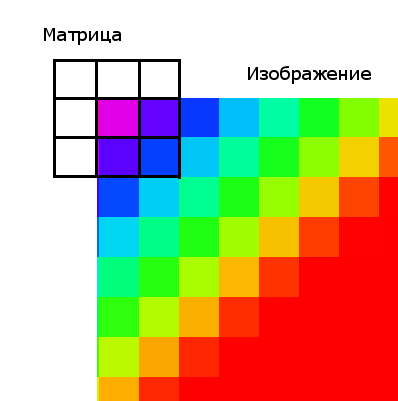
Фильтр использует входное изображение и бинарную матрицу. Бинарная матрица определяет форму окрестности. Обычно окрестность имеет круглую форму.
Фильтр наращивание может быть использован для увеличения бликов, ярких отражений.
В статье были описаны некоторые из фильтров обработки изображения, описаны их алгоритмы и особенности применения.
ru.wikipedia.org/wiki/Медианный_фильтр
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Математическая_морфология
habrahabr.ru/post/43895
Матрица свёртки
Фильтров использующих матрицу свёртки много, ниже будут описаны основные из них.
Матрица свёртки – это матрица коэффициентов, которая «умножается» на значение пикселей изображения для получения требуемого результата.
Ниже представлено применение матрицы свёртки:
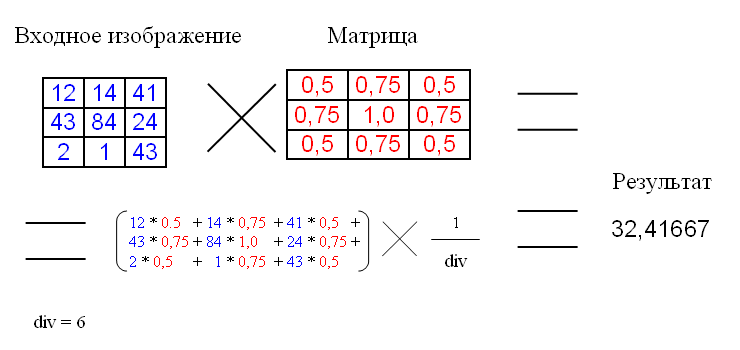
div – это коэффициент нормирования, для того чтобы средняя интенсивность оставалась не изменой.
В примере матрица имеет размер 3x3, хотя размер может быть и больше.
Фильтр размытия
Наиболее часто используемым фильтром, основанным на матрице свёртки, является фильтр размытия.
Обычно матрица заполняется по нормальному (гауссовому закону). Ниже приведена матрица размытия 5x5 заполненная по закону Гауссовского распределения.
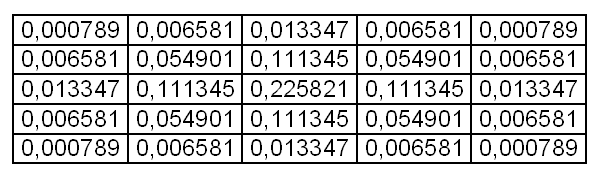
Коэффициенты уже являются нормированными, так что div для этой матрицы равен одному.
От размера матрицы зависит сила размытия.

Стоит упомянуть о граничных условиях (эта проблема актуальна для всех матричных фильтров). У верхнего левого пикселя не существует «соседа» с права от него, следовательно, нам не на что умножать коэффициент матрицы.
Существует 2 решения этой проблемы:
1. Применение фильтра, только к «окну» изображения, которое имеет координаты левого верхнего угла [kernelSize / 2, kernelSize / 2], а для правого нижнего [width — kernelSize / 2, height — kernelSize / 2]. kernelSize – размер матрицы; width, height – размер изображения.
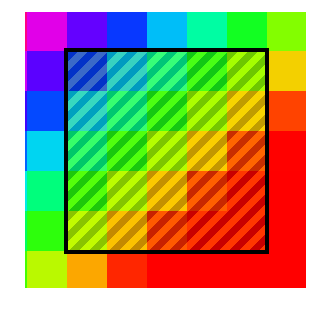
Это не лучший способ, так как фильтр не применяется ко всему изображению. Качество при этом довольно сильно страдает, если размер фильтра велик.
2. Второй метод (дополнение) требует создания промежуточного изображения. Идея в том, чтобы создавать временное изображение с размерами (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). В центр изображения копируется входная картинка, а края заполняются крайними пикселями изображения. Размытие применяется к промежуточному буферу, а потом из него извлекается результат.

Данный метод не имеет недостатков в качестве, но необходимо производить лишние вычисления.
Фильтр размытия по Гауссу имеет сложность O(hi * wi * n *n), где hi, wi – размеры изображения, n – размер матрицы (ядра фильтра). Данный алгоритм можно оптимизировать с приемлемым качеством.
Квадратное ядро (матрицу) можно заменить двумя одномерными: горизонтальным и вертикальным. Для размера ядра 5 они будут иметь вид:

Фильтр применяется в 2 прохода: сначала горизонтальный, а потом к результату вертикальный (или на оборот).
Сложность данного алгоритма будет O(hi * wi * n) + O(hi * wi * n) = 2 * O(hi * wi * n), что для размера ядра больше двух, быстрее, чем традиционный метод с квадратной матрицей.
Фильтр улучшения чёткости
Для улучшения четкости необходимо использовать следующую матрицу:
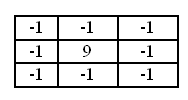
Эта матрица увеличивает разницу значений на границах. Div для этой матрицы равен 1.

В программе GIMP есть фильтр «Матрица свёртки», который упрощает поиск необходимого Вам матричного преобразования.
Более подробную информацию о фильтрах основанных на матрице свёртки вы можете найти в статье «Графические фильтры на основе матрицы скручивания».
Медианный фильтр
Медианный фильтр обычно используется для уменьшения шума или «сглаживания» изображения.

Фильтр работает с матрицами различного размера, но в отличие от матрицы свёртки, размер матрицы влияет только на количество рассматриваемых пикселей.
Алгоритм медианного фильтра следующий:
Для текущего пикселя, пиксели, которые «попадают» в матрицу, сортируются, и выбирается средние значение из отсортированного массива. Это значение и является выходным для текущего пикселя.
Ниже представлена работа медианного фильтра для размера ядра равного трём.
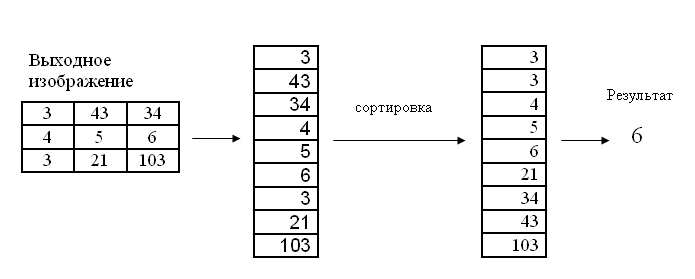
Фильтры эрозия и наращивание
Фильтры наращивание и эрозия служат для получения морфологического расширения или сужения соответственно. Проще говоря, для изображений это значит выбор пикселя с максимальной или минимальной интенсивностью из окрестности.

В результате наращивания происходит увеличение ярких объектов, а эрозии – увеличение тёмных объектов.
Фильтр использует входное изображение и бинарную матрицу. Бинарная матрица определяет форму окрестности. Обычно окрестность имеет круглую форму.
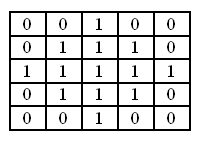
Фильтр наращивание может быть использован для увеличения бликов, ярких отражений.
Заключение
В статье были описаны некоторые из фильтров обработки изображения, описаны их алгоритмы и особенности применения.
ru.wikipedia.org/wiki/Медианный_фильтр
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Математическая_морфология
habrahabr.ru/post/43895






