На Хабре и в сети часто начали появляться статьи, посвященные уязвимостям генераторов случайных чисел. Данная тема крайне обширна и является одной из основных в криптографии. Под катом находится описание случайных чисел от A до Z. Статья является результатом свободного перевода цикла статей из одного западного блога и личных дополнений автора. Основная цель — получить feedback и поделиться знаниями.

Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:
Пусть есть последовательность чисел:

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
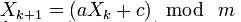
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed'а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
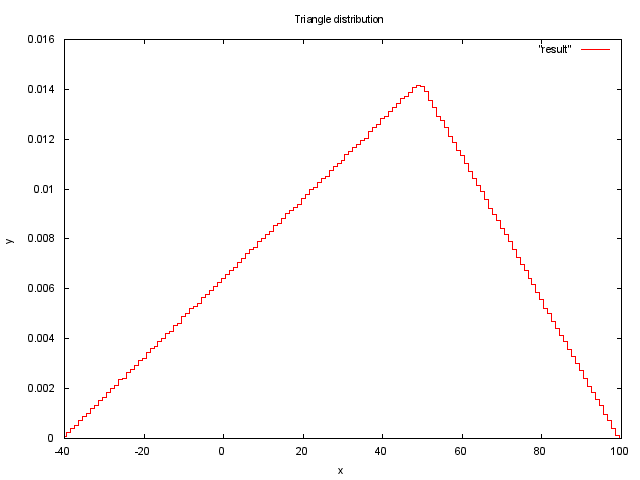
В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так
Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
[1] Дональд Кнут, Искусство программирования (Том 2. Получисленные алгоритмы)
[2] Брюс Шнайер, Прикладная криптография(Глава 16)
[4] www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html
[5] www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html
[6] en.wikipedia.org/wiki/Mersenne_twister
[7] en.wikipedia.org/wiki/Triangular_distribution
[8] ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод
[9] zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf
[10] www.cacert.at/random
[11] www.cs.berkeley.edu/~daw/papers/ddj-netscape.html
[12] www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug
[13] Описан интересный пример генерации через md5 raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.html
jazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.html
jazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.html
jazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html

Введение
Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:
- Генераторы сессий (PHPSESSID)
- Генерация текста для капчи
- Шифрование
- Генерация соли для хранения паролей в необратимом виде
- Генератор паролей
- Порядок раздачи карт в интернет казино
Как отличить случайную последовательность чисел от неслучайной?
Пусть есть последовательность чисел:
1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9. Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
- Предсказуемая зависимость между числами.
- Предсказуемое начальное значение генератора.
- Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
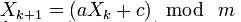
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
public static int a = 45;
public static int c = 21;
public static int m = 67;
public static int seed = 2;
public static int getRand() {
seed = (a * seed + c) % m;
return seed;
}
public static void main(String[] args) {
for(int i=0; i<30; i++)
System.out.println(getRand());
}
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
private static final long multiplier = 0x5DEECE66DL; // 25214903917
private static final long addend = 0xBL; // 11
private static final long mask = (1L << 48) - 1; // 281474976710655 = 2^48 – 1
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
protected int next(int bits) {
long oldseed, nextseed;
AtomicLong seed = this.seed;
do {
oldseed = seed.get();
nextseed = (oldseed * multiplier + addend) & mask;
} while (!seed.compareAndSet(oldseed, nextseed));
return (int)(nextseed >>> (48 - bits));
}
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
((x1*multiplier + addend) & mask) << 16
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
import java.lang.reflect.Field;
import java.util.Random;
import java.util.concurrent.atomic.AtomicLong;
public class PasswordCracking {
public static final long multiplier = 0x5DEECE66DL;
public static final long addend = 0xBL;
public static final long mask = (1L << 48) - 1;
public static void main(String[] args) {
Random random = new Random();
long v1 = random.nextInt();
long v2 = random.nextInt();
long v3 = random.nextInt();
long v4 = random.nextInt();
System.out.println("v1=" + v1 + "\nv2=" + v2 + "\nv3=" + v3 + "\nv4=" + v4);
// brute-force seed
for (int i = 0; i < 65536; i++) {
long seed = (((long) v1) << 16) + i;
int nextInt = (int)(((seed * multiplier + addend) & mask) >>> 16);
if (nextInt == v2) {
System.out.println("Seed found: " + seed);
Random crackingRandom = new Random();
try {
/* set the seed for Random to be convinced that we have found the
right seed because constructor Random (long seed) uses the
private static long initialScramble (long seed) {
return (seed ^ multiplier) & mask;
}
for simplicity will use Reflection */
Field privateSeedField = Random.class.getDeclaredField("seed");
privateSeedField.setAccessible(true);
AtomicLong crackingSeed = (AtomicLong)privateSeedField.get(crackingRandom);
crackingSeed.set(seed);
}catch(Exception e) {
System.out.println(e.toString());
System.exit(1);
}
long cv1 = crackingRandom.nextInt();
long cv2 = crackingRandom.nextInt();
long cv3 = crackingRandom.nextInt();
long cv4 = crackingRandom.nextInt();
System.out.println("Set fiend seed and generate random numbers");
System.out.println("cv1=" + cv1 + "\ncv2=" + cv2 + "\ncv3=" + cv3 + "\ncv4=" + cv4);
break;
}
}
}
}
Вывод данной программы будет примерно таким:
v1 = -1184958941
v2 = 274285127
v3 = -1566774765
v4 = 30466408
Seed found: -77657469128792
Set fiend seed and generate random numbers
cv1 = 274285127
cv2 = -1566774765
cv3 = 30466408
cv4 = -803980434
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
public static long getPreviousSeed(long prevSeed) {
long seed = prevSeed;
// reverse the addend from the seed
seed -= addend; // reverse the addend
long result = 0;
// iterate through the seeds bits
for (int i = 0; i < 48; i++) {
long mask = 1L << i;
// find the next bit
long bit = seed & mask;
// add it to the result
result |= bit;
if (bit == mask) {
// if the bit was 1, subtract its effects from the seed
seed -= multiplier << i;
}
}
System.out.println("Previous seed: " + result);
return result;
}
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Содержимое файла /ext/standard/basic_functions.h
#define MT_N (624)
/* rand.c */
php_uint32 state[MT_N+1]; /* state vector + 1 extra to not violate ANSI C */
php_uint32 *next; /* next random value is computed from here */
int left; /* can *next++ this many times before reloading */
unsigned int rand_seed; /* Seed for rand(), in ts version */
zend_bool rand_is_seeded; /* Whether rand() has been seeded */
zend_bool mt_rand_is_seeded; /* Whether mt_rand() has been seeded */
Содержимое файла /ext/standard/rand.c:
#define N MT_N /* length of state vector */
#define M (397) /* a period parameter */
#define hiBit(u) ((u) & 0x80000000U) /* mask all but highest bit of u */
#define loBit(u) ((u) & 0x00000001U) /* mask all but lowest bit of u */
#define loBits(u) ((u) & 0x7FFFFFFFU) /* mask the highest bit of u */
#define mixBits(u, v) (hiBit(u)|loBits(v)) /* move hi bit of u to hi bit of v */
#define twist(m,u,v) (m ^ (mixBits(u,v)>>1) ^ ((php_uint32)(-(php_int32)(loBit(u))) & 0x9908b0dfU))
/* {{{ php_mt_reload
*/
static inline void php_mt_reload(TSRMLS_D)
{
/* Generate N new values in state
Made clearer and faster by Matthew Bellew (matthew.bellew@home.com) */
register php_uint32 *state = BG(state);
register php_uint32 *p = state;
register int i;
for (i = N - M; i--; ++p)
*p = twist(p[M], p[0], p[1]);
for (i = M; --i; ++p)
*p = twist(p[M-N], p[0], p[1]);
*p = twist(p[M-N], p[0], state[0]);
BG(left) = N;
BG(next) = state;
}
/* }}} */
/* {{{ php_mt_initialize
*/
static inline void php_mt_initialize(php_uint32 seed, php_uint32 *state)
{
/* Initialize generator state with seed
See Knuth TAOCP Vol 2, 3rd Ed, p.106 for multiplier.
In previous versions, most significant bits (MSBs) of the seed affect
only MSBs of the state array. Modified 9 Jan 2002 by Makoto Matsumoto. */
register php_uint32 *s = state;
register php_uint32 *r = state;
register int i = 1;
*s++ = seed & 0xffffffffU;
for( ; i < N; ++i ) {
*s++ = ( 1812433253U * ( *r ^ (*r >> 30) ) + i ) & 0xffffffffU;
r++;
}
}
/* }}} */
/* {{{ php_mt_srand
*/
PHPAPI void php_mt_srand(php_uint32 seed TSRMLS_DC)
{
/* Seed the generator with a simple uint32 */
php_mt_initialize(seed, BG(state));
php_mt_reload(TSRMLS_C);
/* Seed only once */
BG(mt_rand_is_seeded) = 1;
}
/* }}} */
/* {{{ php_mt_rand
*/
PHPAPI php_uint32 php_mt_rand(TSRMLS_D)
{
/* Pull a 32-bit integer from the generator state
Every other access function simply transforms the numbers extracted here */
register php_uint32 s1;
if (BG(left) == 0) {
php_mt_reload(TSRMLS_C);
}
--BG(left);
s1 = *BG(next)++;
s1 ^= (s1 >> 11);
s1 ^= (s1 << 7) & 0x9d2c5680U;
s1 ^= (s1 << 15) & 0xefc60000U;
return ( s1 ^ (s1 >> 18) );
}
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
public static long unBitshiftRightXor(long value, long shift) {
// we part of the value we are up to (with a width of shift bits)
long i = 0;
// we accumulate the result here
long result = 0;
// iterate until we've done the full 32 bits
while (i * shift < 32) {
// create a mask for this part
long partMask = (-1 << (32 - shift)) >>> (shift * i);
// obtain the part
long part = value & partMask;
// unapply the xor from the next part of the integer
value ^= part >>> shift;
// add the part to the result
result |= part;
i++;
}
return result;
}
public static long unBitshiftLeftXor(long value, long shift, long mask) {
// we part of the value we are up to (with a width of shift bits)
long i = 0;
// we accumulate the result here
long result = 0;
// iterate until we've done the full 32 bits
while (i * shift < 32) {
// create a mask for this part
long partMask = (-1 >>> (32 - shift)) << (shift * i);
// obtain the part
long part = value & partMask;
// unapply the xor from the next part of the integer
value ^= (part << shift) & mask;
// add the part to the result
result |= part;
i++;
}
return result;
}
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
long value = output;
value = unBitshiftRightXor(value, 18);
value = unBitshiftLeftXor(value, 15, 0xefc60000);
value = unBitshiftLeftXor(value, 7, 0x9d2c5680);
value = unBitshiftRightXor(value, 11);
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed'а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
double triangular(double a, double b, double c) {
double U = rand() / (double) RAND_MAX;
double F = (c - a) / (b - a);
if (U <= F)
return a + sqrt(U * (b - a) * (c - a));
else
return b - sqrt((1 - U) * (b - a) * (b - c));
}
В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так

Экспоненциальное распределение
Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
Известные взломы генераторов случайных чисел
- Ранние версии протокола шифрования SSL компании Netscape, c малой энтропией [11]
- Уязвимость PHP сессий habrahabr.ru/company/pt/blog/149746
- CryptGenRandom компании Microsoft [12]
- Многие онлайн казино не раз становились объектом атаки через уязвимости в ГПСЧ
Список литературы
[1] Дональд Кнут, Искусство программирования (Том 2. Получисленные алгоритмы)
[2] Брюс Шнайер, Прикладная криптография(Глава 16)
[4] www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html
[5] www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html
[6] en.wikipedia.org/wiki/Mersenne_twister
[7] en.wikipedia.org/wiki/Triangular_distribution
[8] ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод
[9] zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf
[10] www.cacert.at/random
[11] www.cs.berkeley.edu/~daw/papers/ddj-netscape.html
[12] www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug
[13] Описан интересный пример генерации через md5 raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1
Оригинал
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.html
jazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.html
jazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.html
jazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html
