… Танцоры не сводили с нее глаз, а она подпрыгивала и кружила между ними, каждый раз оказываясь там, где никого не было.
сэр Терри Пратчетт "Зимних дел мастер"
Несмотря на всю свою неказистость, "Крестики-нолики" являются краеугольным камнем мира настольных игр. Принцип "N в ряд" настолько прост и естественен, что был независимо изобретён сразу несколькими древними народами. В Китае и Японии он лёг в основу таких игр как "Рендзю" и "Хасами Сёги", в древней Европе — породил "Мельницу" — прародительницу "Алькуэрка" и, в конечном итоге, всего разнообразия современных шашек.
В своём исходном виде, «Крестики-нолики» не кажутся игрой сколь нибудь интересной. В самом деле, беспроигрышная стратегия, для каждого из игроков, в этой игре, совершенно очевидна, а победить, при правильной игре, совершенно невозможно. Подобная игра может привлечь к себе младших школьников, но никак не серьёзных игроков. Впрочем, есть несколько способов всё исправить…
Причём тут кот?
Когда речь заходит об улучшении «Крестиков-ноликов», первое, что приходит в голову — увеличение размеров (или размерности) игрового пространства. Действительно, игра на доске 3x3x3 уже не столь тривиальна, а среди множества разновидностей игры на большой доске имеются дисциплины считающиеся профессиональными (правда, в этом случае, речь идёт о выстраивании пяти фигур в ряд). Существуют и менее очевидные возможности улучшения игры. Так, задействовав в качестве одного из игровых факторов гравитацию, мы получим очень занимательную игру "Четыре в ряд", а простое изменение условия победы (игрок, вынужденно построивший ряд из трёх фигур — проигрывает) даёт нам «Losing Tic-Tac-Toe», победить в котором совсем не просто.
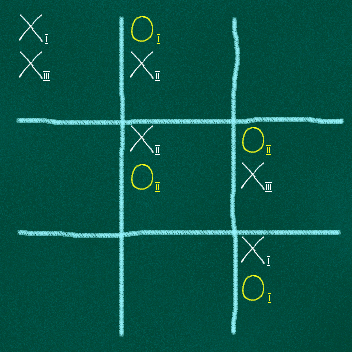
В 2006 году, Allan Goff придумал ещё один способ радикального улучшения игры. Сделал он это не просто так, а с целью иллюстрации таких сложных понятий квантовой механики как «суперпозиция», «запутанность» и «свёртка». В предлагаемом им варианте игры, каждый игрок, вместо того чтобы поставить свой крестик или нолик, делает два полухода в разные позиции игрового поля. Добавленная на доску фигура равновероятно присутствует в двух позициях одновременно. В индексах сохраняется информация об очерёдности ходов игроков, в дальнейшем используемая при разрешении возникающих коллизий.
До тех пор, пока фигуры присутствуют на доске лишь в форме полуходов, мы не можем сказать точно, в какой из позиций каждая из них находится. Возможно, это не самая удачная метафора квантовой механики, поскольку в рамках этой модели каждая фигура может быть «размазана» не более чем по двум возможным расположениям (также возможны некоторые сложности с определением победителя, о которых я скажу ниже). В 2010 году J. N. Leaw и S. A. Cheong предложили более сложный вариант игры, в котором каждый ход представляет собой вектор в девятимерном гильбертовом пространстве. Краткое описание можно посмотреть здесь.
Разумеется, идея ''размазывания'' ходов не нова
Так например, в Refusal Chess (Fred Galvin, 1958), каждый игрок предлагал два возможных хода, а его оппонент выбирал один ход из предложенных. Исключение делалось лишь для позиций с единственным возможным разрешённым ходом. Сходным образом игровой процесс построен в "Ambiguous Chess" (Fabrice Liardet, 2005). В этой разновидности игры, игрок помечает поле на которое собирается сходить (оно может быть занято вражеской фигурой), а его противник выбирает фигуру, способную выполнить этот ход:
В любом случае, концепция показалась мне интересной. Настольные игры, в основе своей, просты. Фигуры ставятся на доску, перемещаются, превращаются, забирают другие фигуры — всё это очень легко реализовать. Но встречаются «изюминки», сложность которых буквально «зашкаливает». В Шахматах, это концепции шаха и мата, в Шашках — «правило большинства», в Го — взаимное влияние фигур. Концепции «суперпозиции» и связанной с ней «запутанности» — одна из таких «изюминок».
Распутываем запутанности
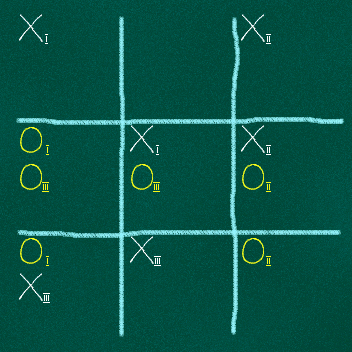
Если бы дело ограничивалось одними лишь полуходами, в «Квантовых крестиках-ноликах» не было бы ничего интересного. Для победы необходимо обеспечить стопроцентное присутствие фигур на заданных позициях! Каким образом полуходы превращаются в полноценные фигуры? Пришло время в этом разобраться. Если заполнять доску полуходами достаточно долго, рано или поздно возникнет ситуация, подобная следующей:
Возникла коллизия, своего рода парадокс — противоречие в исходных данных. В конечном итоге, расположение каждой фигуры должно быть точно определено. Все полуходы должны быть «свёрнуты», но существуют две принципиально различных возможности такой «свёртки». В одном из этих случаев, игра заканчивается.
Игрок, замкнувший цикл взаимозависимостей, виновен в возникновении «парадокса». По этой причине, выбор варианта свёртки предоставляется его оппоненту. В нашем случае, цикл был замкнут «крестиками». Это означает, что «ноликам» удастся избежать поражения. Они просто выберут «из двух возможных миров» тот, в котором «крестики» ещё не победили. Но возможны ситуации, в которых от выбора варианта свёртки уже ничего не зависит:
Что здесь не выбирай, конечный итог для «ноликов» одинаков — они проиграли. Возможна и вырожденная ситуация. Любой из игроков может сделать два полухода в одну и ту же область доски. Это самая короткая из возможных коллизий. Поскольку она подразумевает «выбор» из двух совершенно одинаковых вариантов, такая последовательность полуходов фактически равноценна полному ходу в это поле:
Обратите внимание на то, как ход «крестиков» вытесняется с выбранного поля. Каждая ячейка доски может содержать результат не более чем одного «полного» хода. Такое «вытеснение» может распространяться далее, по цепочке (на самом деле, по дереву). На мой взгляд, подобные ходы находятся где-то на грани фола. Они слишком сильные. Такой «детерминированный» ход равносилен обычному ходу в «Крестиках-ноликах» и, кроме того, позволяет «вытеснить» противника с выбранной позиции. В большей части вариантов своей реализации «Квантовых крестиков-ноликов» (6 из 10) я запретил выполнение «детерминированных» ходов.
Как это всё работает?
Этот код — воплощение ночных кошмаров. Я трижды переписывал его! Теперь он как-то работает. Я не очень хорошо понимаю как, поскольку, в настоящий момент, он, в основном, состоит из заплаток. Сам процесс отладки Axiom-приложений непрост. Если в коде есть ошибки — он падает. В большинстве случаев. Но если всё работает — это вовсе не означает, что ошибок нет. Просто сами ошибки становятся причудливее. И да, без рекурсии дело не обошлось.
Как бы там ни было, это сердце всего проекта. Самым сложным оказалось само определение факта наличия коллизии, а также поиск всех фигур входящих в неё. Процесс «распутывания» можно начинать только с этих фигур. И пока есть коллизия, а она может быть только одна, нельзя разрешать никакие другие ходы кроме «распутывания». В противном случае, есть шанс окончательно всё запутать. Это не сложно. Помогают приоритеты. Если имеется хотя бы один приоритетный ход, никакие другие ходы выполняться не могут. Это не самый универсальный механизм, но он работает:
Оставшаяся часть проста. Даже корректное выполнение свёртки не столь сложно. Грег придумал специальные функции для работы с кольцевым буфером, но я, к стыду своему, так ни разу ими и не воспользовался. Старый добрый трюк с добавлением в конец массива, по которому идут итерации, всё ещё работает:
: in-collision? ( -- ? )
FALSE 0 BEGIN
DUP curr-size @ < IF
DUP pos[] @ here = IF
2DROP TRUE 0
TRUE
ELSE
1+ FALSE
ENDIF
ELSE
TRUE
ENDIF
UNTIL DROP
;
: pair-found? ( -- ? )
FALSE 0 BEGIN
DUP empty-at? NOT OVER piece-type-at piece-type = AND IF
DUP here <> IF
DUP 0 pos[] @ = IF
collision-size @ 0= IF
curr-size @
collision-size !
ENDIF
DROP ALL
ELSE
DUP to
here curr-size @ pos[] !
curr-size ++
2DROP TRUE ALL
ENDIF
ENDIF
ENDIF
1+ DUP ALL >=
UNTIL DROP
;
: not-prev? ( -- ? )
curr-size @ 0> IF
curr-size @ 1- pos[] @ here <>
ELSE
TRUE
ENDIF
;
: try-pos ( -- )
down DROP
BEGIN here
my-empty? NOT not-prev? AND IF
here curr-size @ pos[] !
curr-size ++
pair-found? curr-size @ TOTAL < AND IF
RECURSE
curr-size --
ENDIF
curr-size --
ENDIF
to up NOT my-empty? OR collision-size @ 0> OR
UNTIL
;
: check-collision ( -- )
find-mark
try-pos
collision-size @
DUP 2 > verify
curr-size !
from to
in-collision? verify
;
Как бы там ни было, это сердце всего проекта. Самым сложным оказалось само определение факта наличия коллизии, а также поиск всех фигур входящих в неё. Процесс «распутывания» можно начинать только с этих фигур. И пока есть коллизия, а она может быть только одна, нельзя разрешать никакие другие ходы кроме «распутывания». В противном случае, есть шанс окончательно всё запутать. Это не сложно. Помогают приоритеты. Если имеется хотя бы один приоритетный ход, никакие другие ходы выполняться не могут. Это не самый универсальный механизм, но он работает:
{move-priorities
{move-priority} high-priority
{move-priority} normal-priority
{move-priority} low-priority
move-priorities}
{moves p-drop
{move} select-piece {move-type} high-priority
{move} drop-half {move-type} normal-priority
{move} drop-piece {move-type} normal-priority
{move} Pass {move-type} low-priority
moves}
{pieces
{piece} M {drops} p-drop
{piece} x1
{piece} o1
{piece} x2
{piece} o2
{piece} x3
{piece} o3
{piece} x4
{piece} o4
{piece} x5
{piece} X1 1 {value}
{piece} O1 1 {value}
{piece} X2 2 {value}
{piece} O2 2 {value}
{piece} X3 3 {value}
{piece} O3 3 {value}
{piece} X4 4 {value}
{piece} O4 4 {value}
{piece} X5 5 {value}
pieces}
Оставшаяся часть проста. Даже корректное выполнение свёртки не столь сложно. Грег придумал специальные функции для работы с кольцевым буфером, но я, к стыду своему, так ни разу ими и не воспользовался. Старый добрый трюк с добавлением в конец массива, по которому идут итерации, всё ещё работает:
: add-position ( -- )
0 BEGIN
DUP here <> OVER empty-at? NOT AND IF
DUP piece-type-at piece-type = OVER not-in-position? AND curr-size @ ALL < AND IF
DUP curr-size @ pos[] !
curr-size ++
ENDIF
ENDIF
1+ DUP ALL >=
UNTIL DROP
;
: mark-all ( player -- )
marked-player !
here curr-pos !
down DROP
mr verify marked-player @ mark create-player-piece-type
down DROP
BEGIN
empty? NOT here curr-pos @ <> AND piece-type mark > AND IF
add-position
ENDIF
marked-player @ mark create-player-piece-type
up NOT
UNTIL
;
: untangle ( -- )
0 BEGIN
DUP curr-size @ < IF
DUP pos[] @
to player piece-type OVER mark-all
down DROP
bg verify
DIM + create-player-piece-type
1+ FALSE
ELSE
TRUE
ENDIF
UNTIL DROP
;
Остался ещё один не рассмотренный вопрос. Игра завершается, когда одному из игроков удаётся построить линию из крестиков или ноликов (конечно, в обычных «Крестиках-ноликах» такое происходит крайне редко), но в нашем безумном квантовом мире крестики и нолики могут построить свои линии одновременно! Кого считать победителем?
Allan Goff предлагает вновь задействовать индексы, использованные для нумерации ходов. Для каждой построенной линии должен быть найден максимальный индекс. Тот, у кого этот индекс оказался меньше, побеждает. Поскольку, в своей работе, он использует сквозную нумерацию ходов (X1, O2, X3,...), при наличии линии, победитель будет всегда. Легко заметить, что я использую другую схему нумерации и, в моём случае, вновь получается ничья.
Что заставило меня отойти от канонов? Два соображения. Во первых, сквозная схема нумерации даёт очень серьёзное преимущество первому игроку. На мой взгляд, игровой баланс гораздо важнее гипотетической возможности получения ничьей (серьёзно, в «Квантовых крестиках-ноликах», ничья — редкая ситуация). Что ещё важнее, сквозная нумерация (и связанная с ней методика определения победителя) совершенно неприемлема для «Квантового Морриса», речь о котором пойдёт ниже. Там, у каждого из игроков, всего по три фигуры.
Танцуют все!
Танец Морриса — древнейший английский обычай, связанный с ритуалами плодородия. Желающим проникнуться духом этого действа с удовольствием рекомендую «Зимних дел мастера» за авторством Терри Пратчетта. Про сам танец там рассказано вскользь, но зато от души! В рамках нашего повествования, более важна связь этого обычая с целым семейством настольных игр, невероятно популярным в средневековой Европе. Младшая игра семейства ("Танец трёх мужчин") — ещё один способ «улучшения» крестиков-ноликов. Фактически, это связующее звено между ними и более поздними играми с подвижными фигурами, такими как "Лиса и гуси" или "Алькуэрк".
В основе игры лежит очень простая идея: если не удалось построить ряд сразу, то всё ещё можно победить, двигая уже выложенные фишки по очереди! Чтобы было куда двигаться, каждый игрок использует всего по три фигуры (этого достаточно для построения линии). В старших играх семейства, таких как "Танец девяти мужчин", игрок, построивший ряд («мельницу»), имеет право безвозвратно «смолоть» любую фигуру противника, уже поставленную на доску. В нашем случае, поскольку фигур с каждой стороны всего по три, потеря любой из них означает безусловное поражение. Двух фигур недостаточно для построения ряда!
Отсюда до «Квантового Морриса» всего один шаг! Хотя проблема «ничейной смерти» уже не стоит в «Квантовых крестиках-ноликах» столь остро, сама игра остаётся слишком быстротечной. Ограничение количества фигур до трёх (с каждой стороны) и их перемещение после выставления на доску, помогут «растянуть» игру, добавив в неё зрелищности и неожиданности.
Легко заметить, что перемещаются лишь малые «полуфигуры». Также возможно «расщепление» полной фигуры на две полуфигуры, с перемещением одной из них на другую позицию. Большую фигуру перемещать нельзя. Как и в «Квантовых крестиках-ноликах», существует возможность «детерминированных» ходов. Помимо «сброса» двух полуходов в одну ячейку, мы можем «слить» полуфигуры, перемещая одну из них к другой. Я по-прежнему считаю такие ходы излишне сильными и запрещаю их в части вариантов игры.
Срываем покровы
Рассмотрим один из предыдущих скриншотов, используя слегка изменённый набор графических ресурсов. Всё тайное немедленно становится явным:

Эти тёмно-зелёные кружочки — вспомогательные фигуры, невидимые при нормальной работе приложения. Для чего они? Начнём с ячейки содержащей два кружочка. Вспомогательная фигура, расположенная в правом нижнем углу — маркер. Им отмечается область доски, в которой выполнялся последний ход. С этой позиции можно начинать поиск коллизии. Если коллизия есть, одна из областей входящих в неё обязательно будет помечена. В принципе, можно было бы обойтись и без маркеров, но мне не хотелось усложнять и без того сложный алгоритм поиска коллизий. Очевидно, что эту ячейку можно использовать совершенно безопасно. Каждая область доски может содержать не более восьми малых фигур.
Кружочек по центру — более интересный объект. Дело в том, что малые фигуры добавляются в ячейки доски по порядку, а не в то место куда выполняется сброс (drop) фигуры через пользовательский интерфейс. Соответственно, и сбрасывается не сама фигура, а вспомогательный невидимый маркер. Почему он не удаляется? Игра использует две доски (grid), наложенные одна поверх другой. В 9x9 хранятся малые фигуры, а в 3x3 — большие. Если я буду удалять сбрасываемый маркер, то разрушу изображение на укрупнённой доске. На видео заметно, что изображение всё равно разрушается (при расщеплении больших фигур), но этот эффект кратковременен. Кроме того, с ним я ничего поделать не могу.
Забавнее всего назначение девяти кружочков, расположенных в одной области с крупной фигурой. Здесь мы вновь имеем дело с издержками пользовательского интерфейса. Ячейки доски 9x9 расположены поверх крупной сетки и практически полностью перекрывают её фигуры. В игре Морриса, фигуры необходимо двигать. В том числе и крупные (при этом происходит их расщепление). Но для того, чтобы подвинуть фигуру, необходимо иметь возможность «зацепить» её мышью, а для фигур на сетке 3x3 сделать это довольно проблематично (даже если над ними нет никаких фигур). Пришлось добавить «рукоятки», дёргая за которые можно расщеплять крупные фигуры.
Эти тёмно-зелёные кружочки — вспомогательные фигуры, невидимые при нормальной работе приложения. Для чего они? Начнём с ячейки содержащей два кружочка. Вспомогательная фигура, расположенная в правом нижнем углу — маркер. Им отмечается область доски, в которой выполнялся последний ход. С этой позиции можно начинать поиск коллизии. Если коллизия есть, одна из областей входящих в неё обязательно будет помечена. В принципе, можно было бы обойтись и без маркеров, но мне не хотелось усложнять и без того сложный алгоритм поиска коллизий. Очевидно, что эту ячейку можно использовать совершенно безопасно. Каждая область доски может содержать не более восьми малых фигур.
Кружочек по центру — более интересный объект. Дело в том, что малые фигуры добавляются в ячейки доски по порядку, а не в то место куда выполняется сброс (drop) фигуры через пользовательский интерфейс. Соответственно, и сбрасывается не сама фигура, а вспомогательный невидимый маркер. Почему он не удаляется? Игра использует две доски (grid), наложенные одна поверх другой. В 9x9 хранятся малые фигуры, а в 3x3 — большие. Если я буду удалять сбрасываемый маркер, то разрушу изображение на укрупнённой доске. На видео заметно, что изображение всё равно разрушается (при расщеплении больших фигур), но этот эффект кратковременен. Кроме того, с ним я ничего поделать не могу.
Забавнее всего назначение девяти кружочков, расположенных в одной области с крупной фигурой. Здесь мы вновь имеем дело с издержками пользовательского интерфейса. Ячейки доски 9x9 расположены поверх крупной сетки и практически полностью перекрывают её фигуры. В игре Морриса, фигуры необходимо двигать. В том числе и крупные (при этом происходит их расщепление). Но для того, чтобы подвинуть фигуру, необходимо иметь возможность «зацепить» её мышью, а для фигур на сетке 3x3 сделать это довольно проблематично (даже если над ними нет никаких фигур). Пришлось добавить «рукоятки», дёргая за которые можно расщеплять крупные фигуры.
«Квантовые крестики-нолики» являются, возможно не идеальной, но весьма удачной иллюстрацией идей квантовой механики. Эта игра привлекает к себе внимание. Она используется при проведении соревнований по программированию, вопросы на эту тему периодически появляются на StackExchange. В настоящее время, не составляет труда найти её программную реализацию. Она разработана как для Android так и для iOS. Особо нетерпеливые могут играть непосредственно через Web-интерфейс. Одними лишь «Крестиками-ноликами» набор «квантовых» игр не ограничивается. В качестве бонуса, могу порекомендовать еще и эту игру.
Всех с пятницей, Господа!
