Речь пойдёт о картографии, имеющей дело с фантастическими мирами.
На данный момент процедурная генерация карт это уже обширная тема получившая развитие, главным образом, в рамках гейм-индустрии. Существуют способы автоматической генерации различных типов карт от простых изображений в ролевых и экшен играх до tile-карт в стратегических играх. Первые дают представления о месте действия игры и отличаются маленьким охватом территории, вторые могут моделировать обширные области целых планет, но имеют малую детализацию.
Давно и хорошо известны методы создания карт и рельефов для небольших территорий:
метод срединного смещения, метод шумовых функций (Noise Functions). Сравнительно недавно появился интересный способ основанный на разбиении плоскости полигонами Polygonal Map Generation for Games. Существует сайт, где собраны ссылки на различные ресурсы по искусственной генерации рельефов.
Как правило, чаще всего, дело ограничивается созданием текстур для моделирования ландшафта, но какой бы красивый и зрелищный не получился ландшафт, это ещё не является полноценной картой.
Вообще, будем отличать в дальнейшем рельеф от карты: рельеф считаем разновидностью текстуры и имеем возможность его наблюдать, в отличие от рельефа, карту можем „пощупать“, это подразумевает, что объекты карты должны быть самостоятельными сущностями и существует определённый способ, которым можно их изменять. К тому же, наличие карты не отменяет существование и наблюдение рельефа.
Существует множество программных средств и стандартов для работы с картами Земли. Географические информационные системы предназначены для захвата, манипуляции, анализа и представления всех типов географических данных. OpenStreetMap (OSM) является одним из примеров GIS, который призван собирать географические данные и выдавать их в свободный доступ.
Широкий спектр разнообразных GIS, а так же множество программных средств и техник, появившихся в результате развития проекта OpenStreetMap, просто напрашивается использовать для работы с картами фантастических планет. Если бы такие уже существовали как существует Земля с ее поверхностью.
Далее описываю предлагаемый способ генерации планеты (на пальцах). Делая рельеф планетарного масштаба довольно быстро приходишь к пределам вычислительной системы. Количество производимых вычислений увеличивается квадратично по отношению к уменьшению шага между точками сетки на сфере. В этом главная причина, по которой карты планетарного масштаба не создавались. Вторая из причин — необходимость реализации глобальной речной сети и связывания ее с рельефом.
Приступая к этой задаче первое желание, которое возникает, это избежать вычисления тригонометрических функций, но на сфере это не представляется возможным. Существует способ, когда для создания текстуры на сфере она, сначала, рисуется на гранях правильного многогранника, например куба, и затем отображается на сферу. Понятно, что углы многогранника при таком отображении должны давать искажения. Применение такого способа к большой планете вызвало бы чересчур заметные искажения. Будем использовать другую разновидность этого подхода.
Без разрывов отображаем сферу планеты на соединённые в основании круглые конусы, линия экватора, при этом, должна совпадать с линией соединения конусов. В конце процесса построения рельефа на конусах делаем обратное отображение на сферу. Конечно, искажений не избежать, но, делая отображения по-разному, возможно различно распределить результирующие искажения на сфере. Хорошая новость — полностью избавляемся от вычисления тригонометрических функций.
В качестве рабочего отображения используем вариант, при котором сохраняются расстояния по меридианам. По вертикали мы избегаем искажений совсем, а по горизонтали искажения растут линейно, и около полюсов рост искажений уменьшается, достигая максимума 1.57.
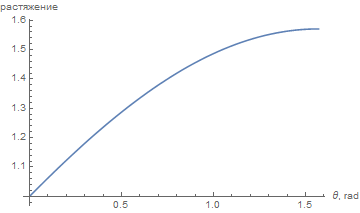
Такое отображение хорошо подходит к планетам, у которых вблизи полюсов океаны или белые пятна. У экватора или в средних широтах визуально заметить привносимые искажения трудно (искажения, привносимые выбранной основной сеткой, могут быть заметны сильнее).
Даже, с учётом упрощения с помощью конической проекции, вычисления для всей планеты остаются затратными по расходу памяти. Для решения этой проблемы прибегаем к двухуровневой генерации. Сначала генерируем основную или глобальную сетку высот. Основным параметром этой сетки служит величина gn, которая определяет количество делений сетки на четверти экватора равным 2gn. Процесс генерации высот на основной сетке выявляет основные участки сущи. Здесь же устанавливается уровень моря по соотношению количества точек попадающих в сушу и океан.
На примерах планет, которые были изготовлены, gn=7. Что является довольно скромной величиной и, в процессе оптимизации алгоритмов и наращивании „железа“, будет возможность постепенно увеличивать gn для новых планет.
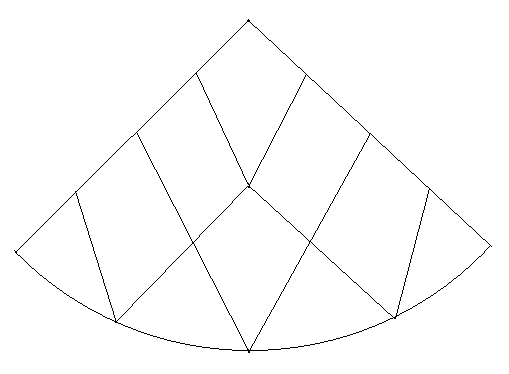
Процесс построения основной сетки. Делим экватор 4*2gn точками на одинаковые отрезки длины l, далее отступаем по нулевому меридиану расстояние l на север и делим параллель, на которой находимся, на 4*(2gn-1) отрезков. Продолжаем процесс далее до полюса, уменьшая при каждой итерации количество точек на каждой следующей параллели на 4. То же самое делаем с южной полусферой. Каждая точка глобальной сетки определяет ромб на конусе (исключения: точки полюсов, которым нет сопоставимых ромбов) и весь двойной конус оказывается поделён на ромбы. Заметим, что это ромбы на поверхности круглого конуса, а не на плоскости. На следующем рисунке изображен фрагмент основной сетки ромбов, содержащий четверть верхнего конуса для gn=2 (без претензии на точность, но полезно для уяснения сути дела).
Переход к сетке на сдвоенных конусах приводит к неожиданному результату: точки основной сетки (без полюсов) компонуются в массив размерностью 2gn на 4*2gn. Для этого сначала заносим в массив точки южного конуса и экватора, а затем справа на свободные места помещаем точки северного конуса, при этом развернув их слева направо. Как следствие, многие алгоритмы в реализации на конусах выглядят проще чем их возможные аналоги на сфере.
Вот, например, как может просто выглядеть код функции увеличивающей высоту окрестности южного полюса радиусом r на единицу (реальная функция в коде проекта выглядит иначе, учитывая более общий случай).
При генерации рельефа на основной сетке стремимся к тому, чтобы образовалось несколько значительных участков суши. Достижение разделения суши на отдельные участки важно для распараллеливания вычислений, так как речная система строится для каждого участка суши независимо. Так выглядит модель планеты изображающей распределение высот основной сетки.

Для перехода на следующий уровень устанавливаем локальную сетку в каждом ромбе и строим рельеф отталкиваясь от уже известных значений высот в вершинах ромба (которые принадлежат основной сетке). Таким образом, итоговый рельеф будет представлять собой разновидность мульти-фрактала.
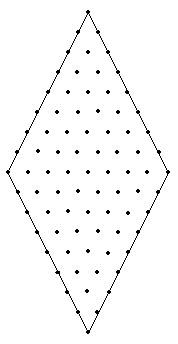
Основной параметр локальной сетки — величина ln, которая задаёт количество шагов сетки в двух направлениях: 2ln+1 и 2*2ln+1 соответственно. На рисунке пример ромба с локальной сеткой при ln=3.
Для генерации рельефа можно осуществить алгоритм, при котором в памяти обязан находится только массив высот одного ромба. Это позволяет осуществить генерацию планет с высоким разрешением объектов карты.
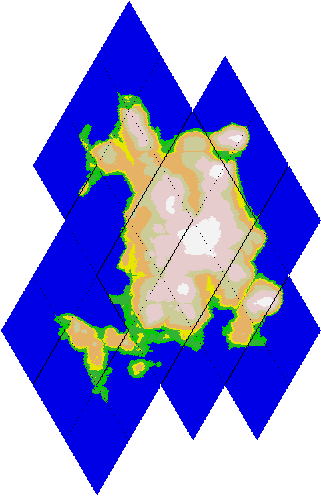
При реализации проектов со сложными и многоэтапными алгоритмами часто есть необходимость построения зрительных образов промежуточных данных. Вот, к примеру, образ средней величины острова в процессе создания планеты; видно деление на ромбы пунктирной линией.
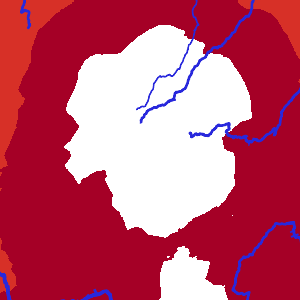
Существует работа посвященная созданию речной системы. Но двухуровневый характер генерации потребовал создать специфические алгоритмы составляющие реки из отдельных кусков. Схематическое изображение рек для небольшого острова смотрите на рисунке. Итоговое изображение рек будет зависеть от их полноводности в устье.
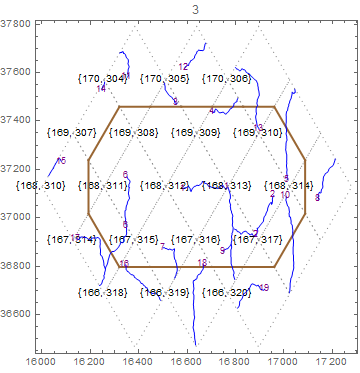
Озера возникают как места локальных минимумов в основной сетке высот. Задача состоит в том, чтобы определить полигон, внутри которого содержится этот локальный минимум.
Несколько красивых фрагментов карт несуществующих миров, которые возникают в результате реализации описанного алгоритма.
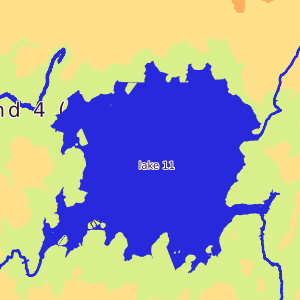
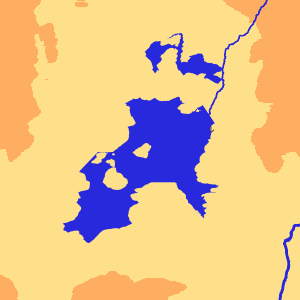

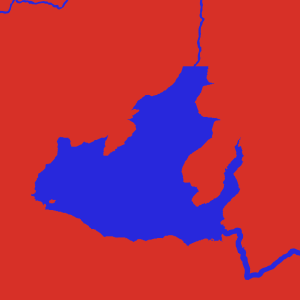

Положение дел с процедурной генерацией карт
На данный момент процедурная генерация карт это уже обширная тема получившая развитие, главным образом, в рамках гейм-индустрии. Существуют способы автоматической генерации различных типов карт от простых изображений в ролевых и экшен играх до tile-карт в стратегических играх. Первые дают представления о месте действия игры и отличаются маленьким охватом территории, вторые могут моделировать обширные области целых планет, но имеют малую детализацию.
Давно и хорошо известны методы создания карт и рельефов для небольших территорий:
метод срединного смещения, метод шумовых функций (Noise Functions). Сравнительно недавно появился интересный способ основанный на разбиении плоскости полигонами Polygonal Map Generation for Games. Существует сайт, где собраны ссылки на различные ресурсы по искусственной генерации рельефов.
Как правило, чаще всего, дело ограничивается созданием текстур для моделирования ландшафта, но какой бы красивый и зрелищный не получился ландшафт, это ещё не является полноценной картой.
Вообще, будем отличать в дальнейшем рельеф от карты: рельеф считаем разновидностью текстуры и имеем возможность его наблюдать, в отличие от рельефа, карту можем „пощупать“, это подразумевает, что объекты карты должны быть самостоятельными сущностями и существует определённый способ, которым можно их изменять. К тому же, наличие карты не отменяет существование и наблюдение рельефа.
GIS и OpenStreetMap как способ представления фантастических карт
Существует множество программных средств и стандартов для работы с картами Земли. Географические информационные системы предназначены для захвата, манипуляции, анализа и представления всех типов географических данных. OpenStreetMap (OSM) является одним из примеров GIS, который призван собирать географические данные и выдавать их в свободный доступ.
Широкий спектр разнообразных GIS, а так же множество программных средств и техник, появившихся в результате развития проекта OpenStreetMap, просто напрашивается использовать для работы с картами фантастических планет. Если бы такие уже существовали как существует Земля с ее поверхностью.
Процедурная генерация планеты
Далее описываю предлагаемый способ генерации планеты (на пальцах). Делая рельеф планетарного масштаба довольно быстро приходишь к пределам вычислительной системы. Количество производимых вычислений увеличивается квадратично по отношению к уменьшению шага между точками сетки на сфере. В этом главная причина, по которой карты планетарного масштаба не создавались. Вторая из причин — необходимость реализации глобальной речной сети и связывания ее с рельефом.
Двойной конус как приближение сферы
Приступая к этой задаче первое желание, которое возникает, это избежать вычисления тригонометрических функций, но на сфере это не представляется возможным. Существует способ, когда для создания текстуры на сфере она, сначала, рисуется на гранях правильного многогранника, например куба, и затем отображается на сферу. Понятно, что углы многогранника при таком отображении должны давать искажения. Применение такого способа к большой планете вызвало бы чересчур заметные искажения. Будем использовать другую разновидность этого подхода.
Без разрывов отображаем сферу планеты на соединённые в основании круглые конусы, линия экватора, при этом, должна совпадать с линией соединения конусов. В конце процесса построения рельефа на конусах делаем обратное отображение на сферу. Конечно, искажений не избежать, но, делая отображения по-разному, возможно различно распределить результирующие искажения на сфере. Хорошая новость — полностью избавляемся от вычисления тригонометрических функций.
В качестве рабочего отображения используем вариант, при котором сохраняются расстояния по меридианам. По вертикали мы избегаем искажений совсем, а по горизонтали искажения растут линейно, и около полюсов рост искажений уменьшается, достигая максимума 1.57.

Такое отображение хорошо подходит к планетам, у которых вблизи полюсов океаны или белые пятна. У экватора или в средних широтах визуально заметить привносимые искажения трудно (искажения, привносимые выбранной основной сеткой, могут быть заметны сильнее).
Два уровня генерации карты
Даже, с учётом упрощения с помощью конической проекции, вычисления для всей планеты остаются затратными по расходу памяти. Для решения этой проблемы прибегаем к двухуровневой генерации. Сначала генерируем основную или глобальную сетку высот. Основным параметром этой сетки служит величина gn, которая определяет количество делений сетки на четверти экватора равным 2gn. Процесс генерации высот на основной сетке выявляет основные участки сущи. Здесь же устанавливается уровень моря по соотношению количества точек попадающих в сушу и океан.
На примерах планет, которые были изготовлены, gn=7. Что является довольно скромной величиной и, в процессе оптимизации алгоритмов и наращивании „железа“, будет возможность постепенно увеличивать gn для новых планет.
Процесс построения основной сетки. Делим экватор 4*2gn точками на одинаковые отрезки длины l, далее отступаем по нулевому меридиану расстояние l на север и делим параллель, на которой находимся, на 4*(2gn-1) отрезков. Продолжаем процесс далее до полюса, уменьшая при каждой итерации количество точек на каждой следующей параллели на 4. То же самое делаем с южной полусферой. Каждая точка глобальной сетки определяет ромб на конусе (исключения: точки полюсов, которым нет сопоставимых ромбов) и весь двойной конус оказывается поделён на ромбы. Заметим, что это ромбы на поверхности круглого конуса, а не на плоскости. На следующем рисунке изображен фрагмент основной сетки ромбов, содержащий четверть верхнего конуса для gn=2 (без претензии на точность, но полезно для уяснения сути дела).

Переход к сетке на сдвоенных конусах приводит к неожиданному результату: точки основной сетки (без полюсов) компонуются в массив размерностью 2gn на 4*2gn. Для этого сначала заносим в массив точки южного конуса и экватора, а затем справа на свободные места помещаем точки северного конуса, при этом развернув их слева направо. Как следствие, многие алгоритмы в реализации на конусах выглядят проще чем их возможные аналоги на сфере.
Вот, например, как может просто выглядеть код функции увеличивающей высоту окрестности южного полюса радиусом r на единицу (реальная функция в коде проекта выглядит иначе, учитывая более общий случай).
import Data.Array.Base
import Data.Array.ST
type Height = Int
type GHeights = UArray (Int,Int) Height
type GHeightsMutable s = (STUArray s (Int,Int) Height)
-- | Make Heights array mutable
thawGHeightsArr :: GHeights -> ST s (GHeightsMutable s)
thawGHeightsArr = unsafeThaw
-- | Increase values around south pole
shiftSouth :: GHeights -> Int -> GHeights
shiftSouth hs r = runSTUArray $ do
a <- thawGHeightsArr hs
mapM_ (\y ->
(mapM_ (\x -> do
v <- readArray a (x,y)
writeArray a (x,y) (v + 1)
) [1..4*y])
) [1..r]
return a
При генерации рельефа на основной сетке стремимся к тому, чтобы образовалось несколько значительных участков суши. Достижение разделения суши на отдельные участки важно для распараллеливания вычислений, так как речная система строится для каждого участка суши независимо. Так выглядит модель планеты изображающей распределение высот основной сетки.

Для перехода на следующий уровень устанавливаем локальную сетку в каждом ромбе и строим рельеф отталкиваясь от уже известных значений высот в вершинах ромба (которые принадлежат основной сетке). Таким образом, итоговый рельеф будет представлять собой разновидность мульти-фрактала.
Основной параметр локальной сетки — величина ln, которая задаёт количество шагов сетки в двух направлениях: 2ln+1 и 2*2ln+1 соответственно. На рисунке пример ромба с локальной сеткой при ln=3.

Для генерации рельефа можно осуществить алгоритм, при котором в памяти обязан находится только массив высот одного ромба. Это позволяет осуществить генерацию планет с высоким разрешением объектов карты.
При реализации проектов со сложными и многоэтапными алгоритмами часто есть необходимость построения зрительных образов промежуточных данных. Вот, к примеру, образ средней величины острова в процессе создания планеты; видно деление на ромбы пунктирной линией.

Реки и озера
Существует работа посвященная созданию речной системы. Но двухуровневый характер генерации потребовал создать специфические алгоритмы составляющие реки из отдельных кусков. Схематическое изображение рек для небольшого острова смотрите на рисунке. Итоговое изображение рек будет зависеть от их полноводности в устье.

Озера возникают как места локальных минимумов в основной сетке высот. Задача состоит в том, чтобы определить полигон, внутри которого содержится этот локальный минимум.
Поэзия карт
Несколько красивых фрагментов карт несуществующих миров, которые возникают в результате реализации описанного алгоритма.





