У того, кто в детстве не писал на Прологе — нет сердца, а у того, кто пишет на нём сегодня — нет мозгов. (оригинал)

Если вас всегда терзали мучительные сомнения — что за фигня это Логическое Программирование (ЛП) и вообще зачем оно нужно? То это статья для вас.

Можно по-разному разделить языки программирования на группы (часто их называют парадигмами программирования), например, вот так:

• структурное: программа разбивается на блоки — подпрограммы (изолированные друг от друга), а основными элементами управления являются последовательность команд, ветвление и цикл.
• объектно-ориентированное: задача моделируется в виде объектов, которые отправляют друг другу сообщения. Объекты обладают свойствами и методами. Абстракция. Инкапсуляция. Полиморфизм. Ну в общем, все в курсе.
• функциональное: базовым элементом является функция и сама задача моделируется в виде функции, а, точнее, чаще всего в виде их композиции, если f(.) и g(.) — это функции, то f(g(.)) — это их композиция.
• логическое: вот тут, как правило, начинается феерия — если про первые три написаны сотни статей, книг, обзоров, презентаций и учебников, то здесь мы в лучшем случае видим что-то про Prolog и разработки времён Pink Floyd и Procol Harum (ну хоть с музыкой им тогда повезло) и на этом история заканчивается.

Вот эту оплошность я и собираюсь сегодня исправить.

Важнейший тезис этой статьи:

Логическое программирование != Prolog.

И вообще последний вам скорее всего не нужен. А вот первое вполне может быть.

Структура статьи:

• Что такое Пролог и почему он вам скорее всего не нужен
• Зачем оно надо, или краткое введение в Answer Set Programming
• Решаем задачи на ASP
• Комбинаторная оптимизация
• Вероятностное ЛП: ProbLog
• ЛП на классической логике FO(.) и IDP
• Sketched Answer Set Programming
• Экспериментальный анализ
• Тестирование и корректность программ
• Заключение

В данной статье (возможно) впервые на русском языке собраны основные аспекты современного логического программирования вместе с объяснением зачем они нужны. Логическое программирование (ЛП) напрямую связано с темой моего PhD (о нем будет отдельный подробный пост). В процессе работы я заметил, что материала на русском языке практически не существует и решил заполнить этот пробел (в русской википедии даже нет статьи про ASP, которую бы стоило написать).

Отдельные части статьи могут быть не связаны с друг другом напрямую, такие какие Sketching и Problog — в некотором смысле это персональный обзор наиболее интересных тем и разработок в области логического программирования. Здесь безусловно не получится покрыть все темы связанные с ЛП — но можно считать, что это первый шаг, чтобы заинтересованный читатель погрузился в тему или представил, что ЛП за зверь такой.

Что такое Пролог и почему он вам скорее всего не нужен

Prolog (Programming in Logic, в оригинале: programmation en logique) был разработан в Марселе в начале 70-х Аленом Колмероэ. В основу языка легла процедурная интерпретация логических выражений Хорна (т.е., как именно можно машинно выполнить) утверждений вида:

a :- b, c, d,...,z.

Что может быть прочитано как: "если условия b, c, d, ..., z — выполнены, тогда и "a" должно быть верно.

И, упрощенно говоря (вот тут мы опускаем все технические детали), может быть переписано в виде логического следования:

По сути Сэр Боб Ковальски — -- придумал такую вещь: утверждение "a" верно, если мы докажем, что все предпосылки к нему верны. (Кстати, отличный и веселый мужик — еще здоров и сыпет шутками и байками, год назад на конференции в Королевском сообществе в Лондоне он прочитал отличную и временами смешную лекцию по истории Пролога и логического программирования.)

В чём соль, Ковальски? Если взять выражение "a :- b,c,d", то его можно прочитать так:

"a" — верно, если я могу: доказать "b", доказать "c" и доказать "d".

Тогда каждая программа — это набор теорем для вывода утверждений, а каждое выражение "доказывается" (внимательный читатель конечно же заметит здесь изоморфизм Карри — Ховарда).

Задача становится чуть веселее, если добавить сюда отрицание. В Прологе оно называется negation as failure и отличается от классического отрицания в логике. В теории это звучит так: если я не смог доказать утверждение "a", то значит оно неверно. В логике такое предположение называется closed world assumption и иногда оно очень даже осмысленно.

Negation as Failure и Closed World Assumption

Представьте себе расписание автобуса 11-го маршрута города Самары, фрагмент:

• 15:15
• 15:45
• 16:15
• 16:45
• 17:15

Вопрос: есть ли автобус в 16:00? Его нет, потому что мы не можем доказать, что он есть согласно расписанию — т.е. расписание обладает полной картиной мира хождения 11-го маршрута в городе Самаре. Отсюда собственно и название closed world assumption — предположение о том, что весь условный мир описан данной программой — всё вне — ложно. Как правило также применяется в базах данных — кстати про них писал тут.

Пролог, как Тьюринг полный язык программирования

Вместе с еще парой интересных операторов (как например cut) из Пролога получается — Тьюринг полный язык — вкратце — если программа на прологе P вычисляет функцию f(x), то найдется программа M на любом другом Тьюринг полном языке, которая тоже вычисляет f(x). Таким образом, если вы можете решить программу на Прологе — значит и на любом другом языке (Python, Java, C, Haskell, etc) можно написать решение. Никаких чакр тут не открывается.

В целом решение задачи на Прологе раскладывается согласно Бобу Ковальски в схему

Algorithm = Logic + Control

Хороший пример задачи, которая хорошо формулируется и решается на прологе, — это набор правил, согласно которому выполняется или нет определенное условие. Однако вам самим придется задать алгоритм поиска решения — что является пространством допустимых значений, в каком порядке они обходятся и тд. По сути вы моделируете задачу в виде правил вывода и с помощью правил вывода задаете процедуру поиска решения (порядок правил, cut, переход от значений в списке из тела правило в голову, и тд) и допустимое пространство решений.

Приведем в качестве примера быструю сортировку на прологе — комментарии мои, код из The Art Of Prolog (если у вас возникнет спонтанное желание читать рэп изучать Пролог, то рекомендую именно эту книгу)

quicksort([X|Xs],Ys) :- % head: X -- pivot element, Xs -- the rest, Ys -- sorted array
                        partition(Xs,X,Littles,Bigs), % X divides Xs into Littles = [x < X for x in Xs], and Bigs
                        quicksort(Littles,Ls),  % The smaller ones are sorted into Ls
                        quicksort(Bigs,Bs), % Same for biggies
                        append(Ls,[X|Bs],Ys). % Then Ys -- output is literally Ls + [X] + Bs
quicksort([],[]). % empty array is always sorted

partition([X|Xs],Y,[X|Ls],Bs) :- X =< Y, partition(Xs,Y,Ls,Bs). % If X an element of the given array is above Y, it goes into biggies
partition([X|Xs],Y,Ls,[X|Bs]) :- X > Y,  partition(Xs,Y,Ls,Bs). % else into littles 
partition([],Y,[],[]). % empty one is always partitioned 

Мы видим, что предикат quicksort определен для двух случаев — пустой и непустой список. Нам интересен непустой случай: в нем список [X|Xs], где X — голова списка, т.е., первый элемент (car — для тех, кому кажется, что в этой программе мало скобочек) и Xs — хвост (tail, он же cdr) разбивается на два списка Bigs и Littles — те, кто больше, и те, кто меньше, Х. Затем оба этих списка рекурсивно сортируются и объединяются в финальный выходной список Ys. Как мы видим в целом мы задаем правилами вывода работу всего алгоритма.

Чем хорош пролог? У него хорошо с формальной семантикой — т.е. можно формально показывать свойства (например доказать, что программа выше и правда сортирует числа), хорошо расширяется на вероятностный случай (см. раздел ProbLog) и вообще хорошо расширяется, удобный язык для моделирования логических задач, хорошо подходит для математических работ, для мета-языковых операций и тд.

Вкратце, если вы не пишите научную работу, где вам нужно формально показать свойства поведения программы — скорее всего вам не очень нужен Пролог. Но может быть вам пригодится логическое программирование?

Зачем оно надо, или краткое введение в Answer Set Programming (ASP)

Краткое объяснение, что такое ASP:

если SAT — это assembler, то современный ASP — это C++.

Вот тут стоит начать с такой штуки, как декларативное программирование и принцип устойчивости к изменениям (elaboration tolerance principle) от Джона Маккарти (который придумал LISP, повлиял на Алгол и вообще предложил термин "Искусственный Интеллект").

Что такое декларативный подход? Если вкратце, то мы описываем задачу и её свойства, а не как её решать. В этом случае задача чаще всего представляется в виде:

Проблема = Модель + Поиск

Где мы регулярно встречаемся с таким подходом? Например, в базах данных SQL — это декларативный язык запросов, а поиском ответа на этот запрос занимается СУБД. Для эффективной работы СУБД придуманы тысячи эффективных алгоритмов, данные хранятся в оптимизированном виде, всюду индексы, методы оптимизации запросов и тд.

Но самое важное, что пользователь видит вершину айсберга: язык SQL. И имея некоторое представление о СУБД пользователь может писать эффективные запросы. Объясним для начала принцип устойчивости к изменениям на простом примере. Допустим, что мы написали простой запрос Q, который считает среднюю зарплату по департаментам компании. Через какое-то время нас попросили немного изменить запрос — например не учитывать в подсчетах менеджмент — нас стала интересовать средняя зарплата технических специалистов. В таком случае, в запрос Q нужно добавить всего лишь условие "role != 'manager'".

Значит, наш новый запрос Q_updated представляется в виде базового запроса + дополнительное условие. Говоря чуть более обще, мы видим, что

Вариация Задачи = Базовая Модель + Доп Условие

А значит, что когда мы немного меняем условие задачи на какое-то дополнительное условие X, нам необходимо изменить модель (которая моделирует изначальную задачу на каком-то формальном языке — например SQL), добавив дополнительное условие C_X.

Причем тут ASP и Логическое программирование?

Ссылки:

• Много материала можно найти на странице профессора Торстена Шауба
• Tutorial Штефана Халбоблера
• Подборка видео tutorial: into into ASP, ASP for Knowledge Representation
• Хороший вводный материал от Томаса Айтера: ASP primer
• Книга ASP in Practice — раньше была в свободном доступе (сейчас что-то не вижу прямой ссылки)

В чем принципиальная разница между Прологом и ASP? По сути ASP — это декларативный язык ограничений, т.е., мы задаем пространство перебора в виде специальных ограничений называемых choice rules, например:

1 { color(X,C) : colors(C) } 1 :- node(X).

Такие правила определяют пространство перебора — буквально читается следующим образом: для каждого X в предикате (читай здесь — во множестве) node, i.e., для каждой вершины X — должен быть верен один — единичка слева от "{" и только один — единичка справа от "}" атом color(X,C), такой что C пришел к нам из множества colors (унарный предикат colors/1).

Одной из главных особенностей ASP является то, что в ограничениях определяется, что НЕ является решением, например — рассмотрим следующее правило:

:- edge(X,Y), color(X,Cx), color(Y,Cy), Cx = Cy. 

Ограничения (в научной англоязычной литературе употребляется термин: integrity constraints) — по сути, правила из самого начала статьи — только у них “пустая голова” ~ empty head: и на самом деле, это сокращение от правил вида:

false :- a_1, a_2, … a_n

т.е. если выполняются a_1, … a_n, то выводится “ложь” и моделью это не является.
(еще точнее: false — это синтаксическая конструкция для b :- a_1, …. a_n, not b. — b выводится в предположении, что b неверно — что является противоречием).

На этом закончим теоретический экскурс и посмотрим на правило внимательнее — оно утверждает следующее: если между X и Y есть дуга, цвет Х — это Cx, а цвет Y — это Сy и Cx == Cy, то это НЕ решение.

Кстати говоря, люди знакомые с ASP, скорее всего записали бы это правило так:

:- edge(X,Y), color(X,C), color(Y,C).

Переменные с одинаковым именем внутри одного и того же правила — считаются равными (и скорее всего это поможет на этапе grounding — но это отдельная история).

Перейдем к описанию всей задачи в целом (и еще парочке).

Разбираем пару популярных комбинаторных задач: NP-полных и не очень

Код, описанный здесь, лучше всего запускать в Clasp (где он перед художественной обработкой и написанием комментариев и тестировался).

Мы поговорим о следующих задачах:

• раскраска графа: дан граф, нужно определить можно ли раскрасить его в три цвета так, что никакие две вершины не раскрашены в один и тот же цвет
• черно-белые королевы: на доске n на n, расставить k черных и белых королев, так что никакие две королевы разных цветов не должны бить друг друга

И решим каждую из них с помощью ASP, а заодно и разберем основные приемы моделирования.

Раскраска графа

Дан граф:

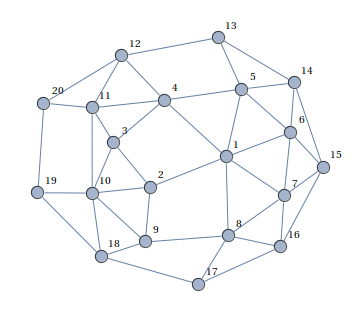
Нужно раскрасить его вершины в три цвета (красный-синий-зеленый), так чтобы никакие две соседние вершины не были одинакового цвета, либо сказать, что это невозможно.

Выход:

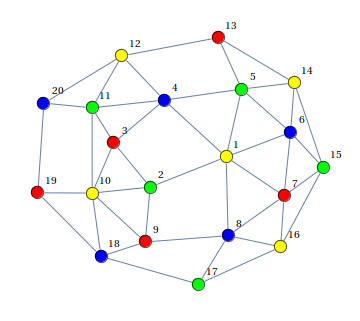
(картинки взяты отсюда)

Основные конструкции ASP кода мы уже разобрали — пройдемся по остальным элементам: node/1 (node(a). node(b)...) — объявляет множество вершин графа, порядок не важен, edge/2 — объявляет дуги. Такие атомы в ASP (и логическом программировании) называются — фактами, фактически это сокращение от “a :- true.”, а выводится просто из утверждения, которое всегда верны, т.е., атомы задают данные программы.

% -- это комментарий, как и всё что идет в строке после символа "%"
% Объявляем четыре вершины графа
node(a). node(b). node(c). node(d).
% Объявляем ребра графа
edge(a,b). edge(a,d).
edge(b,c). edge(b,d).
edge(c,d).
% Говорим, что если между X и Y, есть вершина, то и между Y и X она есть -- делаем граф ненаправленным
edge(Y,X) :- edge(X,Y).
% Объявляем допустимые цвета
colors(red). colors(green). colors(blue).
% Говорим, что для каждой вершины, у неё должен быть один и только один цвет причем из предиката colors(.) выше
1 { color(X,C) : colors(C) } 1 :- node(X).
% Если у вершин X, Y (какого-либо ребра) вдруг один и тот же цвет, ака Cx = Cy, то это НЕ решение 
:- edge(X,Y), color(X,C), color(Y,C).
% Показывать только цвета вершин в выводе
#show color/2.

Черно-белые королевы

Про расстановку королев (включаю эту вариацию) писал раньше подробнее вот здесь.

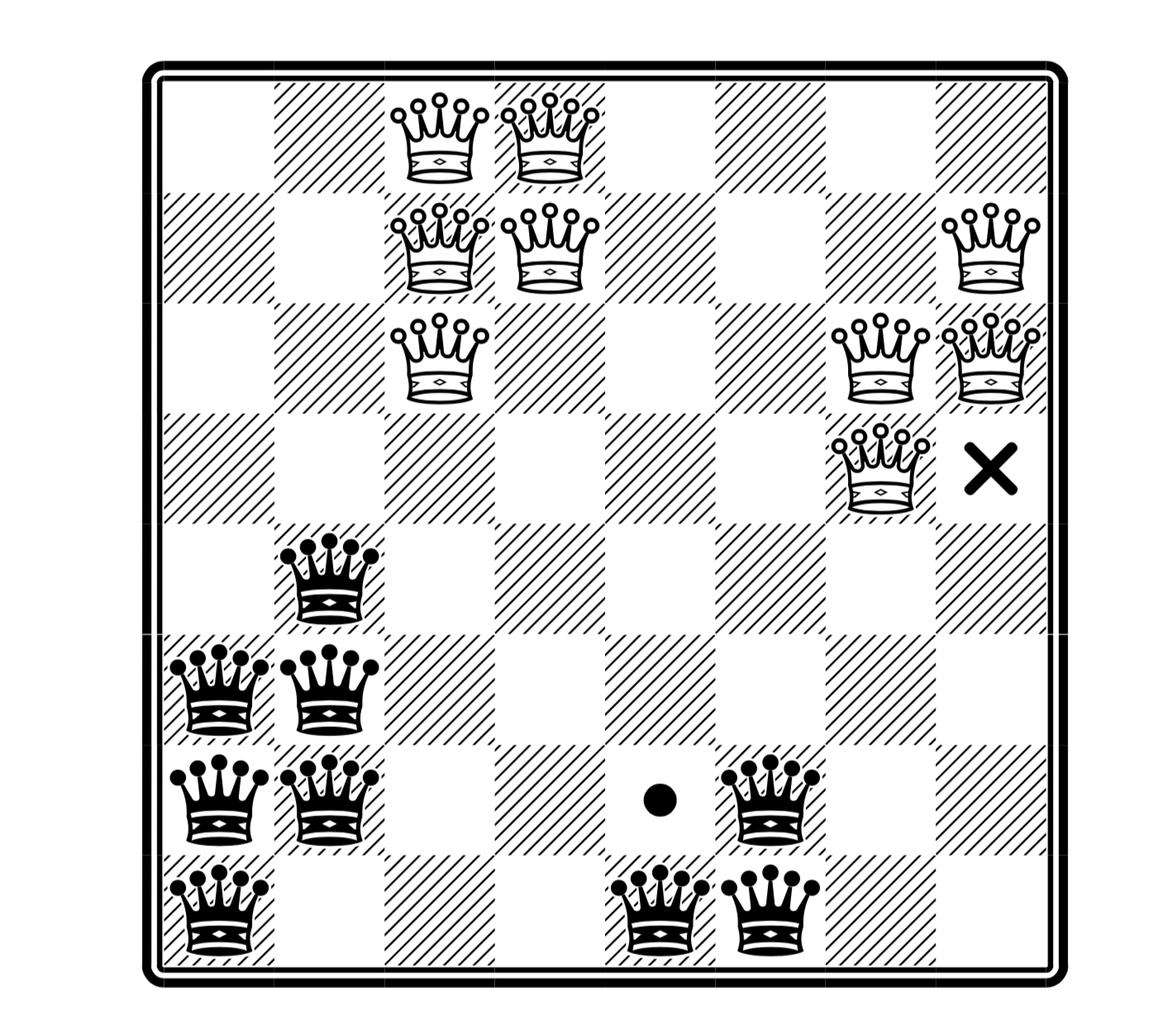
(здесь максимальное число ферзей, причем на месте крестика можно поставить белого, а на месте точке черного — но не обоих сразу; взято из статьи)

Код приведенный здесь решает, как простую полиномиальную версию расстановки королев, так и NP-полную версию (см. хабра-статью про королев; здесь предполагаем, что результат по сложности для классической версии также распространяется и на эту вариацию).

% объявляем размер количество королев каждого цвета "k" и размер доски "m"
#const k=2. 
#const m=4.
% объявляем цвета и размеры доски
color(b). color(w).
col(1..m). row(1..m).
% для каждого цвета должно быть ровно k королев, причем с размерами в пределах доски
k { queen(C,Row,Col) : col(Col), row(Row) } k :- color(C).
% объявляем что НЕ является решением Rw -- row white, Cb -- column black, etc
% если есть белая и черная королевы стоят на одной строке
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw = Rb.
% если есть белая и черная королевы стоят в одной колонке
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw = Cb.
% если есть белая и черная королевы стоят на одной диагонали
:- queen(w,Rw,Cw), queen(b,Rb,Cb), | Rw - Rb | = | Cw - Cb |.

Разберем код чуть подробнее, следующие правила задают параметры доски — по сути, мы могли бы решать задачу и с большим количеством цветов королев — цвета здесь записаны в виде значений предиката color/1.

% объявляем размер количество королев каждого цвета "k" и размер доски "m"
#const k=2. 
#const m=4.
% объявляем цвета и размеры доски
color(b). color(w).
col(1..m). row(1..m).

Далее нам нужно объявить пространство поиска:

% для каждого цвета должно быть ровно k королев, причем с размерами в пределах доски
k { queen(C,Row,Col) : col(Col), row(Row) } k :- color(C).

По сути данное правило читается так: для каждого цвета С, должно быть k и ровно k королев  цвета C, причем значение Row и Col должно быть из множества предикатов col/1 и row/1. Проще говоря, для каждого цвета мы устанавливаем количество корректных (на доске) королев равным k.

Далее мы описываем что не является решением: если мы разного цвета на одной строке, колонке или диагонали:

% если есть белая и черная королевы стоят на одной строке
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw = Rb.
% если есть белая и черная королевы стоят в одной колонке
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw = Cb.
% если есть белая и черная королевы стоят на одной диагонали
:- queen(w,Rw,Cw), queen(b,Rb,Cb), | Rw - Rb | = | Cw - Cb |.

По сути мы видим, что наш код хорошо раскладывается на две части: пространство поиска (guess) + валидация ответа (check) — в ASP это и называется guess-and-check парадигмой, а весь код хорошо ложится на уравнение Problem = Data + Model — в отличие от SAT, если я поменяю данные — добавлю новых королев, то сами ограничения (правила модели) не изменятся. Вообще мы могли бы переписать эти правила, чтобы они даже цвета принимали в качестве параметра.

Кратко о комбинаторной оптимизации

Суть проста: есть комбинаторная задача, как например поиск цикла Гамильтона (NP-полная задача), но сверху есть доп условие: что-то нужно минимизировать — например вес пути (количество цветов для раскраски графа, максимизировать число королев или цветов королев и тд.) Как правило это дает скачок сложности задачи и делает поиск довольно сложным. У ASP есть стандартный механизм для решения задач комбинаторной оптимизации.

Разберем задачу поиска цикла Гамильтона с оптимизацией веса пути (код из книги Answer Set Solving in Practice. Martin Gebser et al.; комментарии — мои)

% === GUESS ===
% задаем пространство поиска -- для каждой вершины должна быть дуга в цикле
1 { cycle(X,Y) : edge(X,Y) } 1 :- node(X). 
% симметрия по дугам
1 { cycle(X,Y) : edge(X,Y) } 1 :- node(Y).
% начинаем в вершине 1
% === AUXILIARY INFERENCE ===
reached(Y) :- cycle(1,Y).
% транзитивное замыкание достижимости вершин
reached(Y) :- cycle(X,Y), reached(X).
% === CHECK ===
% если какая-то из вершин не может быть достигнута -- это НЕ решение
:- node(Y), not reached(Y).
% === MINIMIZE ===
% а еще -- у каждой дуги, есть цена и нужно минимизировать совокупный вес пути
#minimize [ cycle(X,Y) = C : cost(X,Y,C) ].

По сути мы видим, что задача комбинаторной оптимизации в ASP хорошо раскладывается в декларативное уравнение:

Problem Model = Guess + Check + Minimize

Также в задаче присутствует часть вывода новых фактов (auxiliary inference), которые потом используются в ограничениях. Это также довольно стандартно для программ, написанных на ASP.

Вероятностный Prolog — ProbLog

Prolog хорош тем, что он хорошо расширяется — как язык, в том числе и на вероятностный случай — ProbLog (в шутку я читаю его всегда, как Проблох — референс к его фламандскому происхождению и тому, как его читают авторы) — Probabilistic Prolog.

Теоретические основы вероятностного логического программирования изложены в статье

A Statistical Learning Method for Logic Programs with Distribution Semantics by Taisuke Sato

(Он, кстати, еще в трезвом уме и здравой памяти — выступал на ILP 2015 в Киото — где задавал участникам много интересных и коварных вопросов)

Основные материалы по теме можно найти здесь (там же есть онлайн-редактор и tutorial, статьи и тд)

По сути представьте себе, что теперь правила пролога выводят не факт, а вероятность того, что данный факт верен, например, представим, что у нас есть набор нечестных монет, нечестных потому что вероятность выпадения орла не 0.5, а ну например 0.6 — вопрос какова вероятность выпадения орла, если мы подкинем четыре таких монетки?

% Probabilistic facs:
0.6::heads(C) :- coin(C).

% Background information:
coin(c1).
coin(c2).
coin(c3).
coin(c4).

% Rules:
someHeads :- heads(_).

% Queries:
query(someHeads).

В первом правиле мы описываем какие у нас есть случайные величины — это переменные, описывающие выпадение орла (сами факты о монетках — детерминированные), потом мы описываем стохастическую величину — someHeads — выпадение хотя бы одного орла, через имеющиеся у нас вероятностные величины — монетки. И последнее — это запрос: какова вероятность выпадения орла.

По сути ProbLog — это очень удобная система моделирования задач, которые представляются в виде группы правил (например бизнес логики) с вероятностным исходом.

Логическое программирование на классической логике FO(.) и IDP

FO(.) и IDP — это во многом очень схожая система с Answer Set Programming: FO(.) — First Order и (.) — референс к расширениям языка на случай индуктивных определений, агрегации и тд. А IDP — это именно система, которая поддерживает язык FO(.). Здесь и далее мы их не различаем (и вообще это отличие похоже существенно только для авторов — но там как главный идейный создатель FO(.) и IDP Марк Денекер все пять лет моего PhD указывал мне эту разницу, я решил хоть где-то провести различие между ними).

По сути вся разница в том, что вместо правил вывода в духе Пролога мы используем классическую логику. IDP также поддерживает простую систему типов.

/*********************************
    A Sudoku solver in IDP
*********************************/

vocabulary V {

    type row isa int    // The rows of the grid (1 to 9)
    type column isa int  // The columns of the grid (1 to 9)
    type number isa int  // The numbers of the grid (1 to 9)
    type block isa int   // The 9 blocks of 3x3 where the numbers need to be entered

    liesInBlock(row, column, block)
        //This declares which cells belongs to which blocks.
        //This means that liesInBlock(r, k, b) is true if and only if
        // the cell on row r and column c lies in block b.

    solution(row, column) : number
        //The solution: every cell has a number
        //A cell is represented by its row and column.
        //For example: solution(4,5) = 9 means that the cell on row 4 and column 5 contains a 9.
}
theory T : V {

    //On every row every number is present.
    ! r : ! n : ? c : solution(r,c) = n.

    //In every column every number is present.
    ! c : ! n : ? r : solution(r,c) = n.

    //In every block every number is present.
    ! b : ! n : ? r c : liesInBlock(r,c,b) & solution(r,c) = n.

    //Define which cells lie in which block
    {
        liesInBlock(r,k,b) <-
            b = (((r - 1) - (r - 1)%3) / 3) * 3 + (((k - 1)-(k - 1)%3) / 3) + 1.
    }
}

Смысл в том, что мы можем использовать классические функции и привычные кванторы существования и всеобщности. Возьмем пример из Судоку: каждое число должно встречаться на каждой строке. Пусть наше решение — это функция solution(row, column) -> {1,...,9}, тогда должно быть верно следующее:

Проще говоря, для каждой строки и каждого числа есть такая колонка с, что функция на ней отображает (r, c) в n. Именно это ограничение и записано в полном коде выше.

→ Основная ссылка

→ Онлайн редактор

Sketched Answer Set Programming

Лишь вкратце упомяну эту идею — так как это пример одной из разработок в данной области (тем более, что моя разработка, чтобы и не упомянуть действительно). Научная область, объединяющая логическое программирование (logic programming) и машинное обучение (machine learning), ап называется Inductive Logic Programming. В ней происходит много чего интересного и это отдельная история, здесь же приведем лишь один пример связанный с ASP.

Основано на статье Sketched Answer Set Programming by Sergey Paramonov, Christian Bessiere, Anton Dries, Luc De Raedt

Представим, что вы начали изучать ASP и в качестве задания нужно решить черно белых королев — простым гуглением найдем решение на Constraint Programming языке Essense.

Если вы перепишите это ограничения один-в-один на ASP, то получится следующее:

:- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw != Rb.
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw != Cb.
:- queen(w,Rw,Cw), queen(b,Rb,Cb), |Rw - Rb| != |Cw - Cb|.

Что безусловно неверно и будет возвращать Unsatisfiable какую бы строчку мы не убрали. Идея sketching состоит в том, чтобы пометить часть программы как "мы вот тут не уверены, что должно быть" и дать примеры, как должна себя вести программа — "вот это решение, а вот это нет"

[Sketch]
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw ?= Rb.
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw ?= Cb.
:- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw ?+ Rb ?= Cw ?+ Cb.
[Examples]
positive: queen(w,1,1). queen(w,2,2). queen(b,3,4). queen(b,4,3).
negative: queen(w,1,1). queen(w,2,2). queen(b,3,4). queen(b,4,4).

Условно, мы не уверены в операторах арифметики и неравенствах, мы пометили их вопросом, и дали примеры, что является решением, а что нет. По ним мы можем восстановить исходную программу (как в начале статьи).

Помимо sketching люди учатся восстанавливать целые программы с нуля по примерам — но это отдельная история.

Экспериментальный анализ

В качестве прототипа решения

ASP — хорош в качестве прототипа решения сложных комбинаторных задач, особенно, если это вариация сложной задачи — например NP-полная версия N-queens — как уже описывал ранее вот здесь.

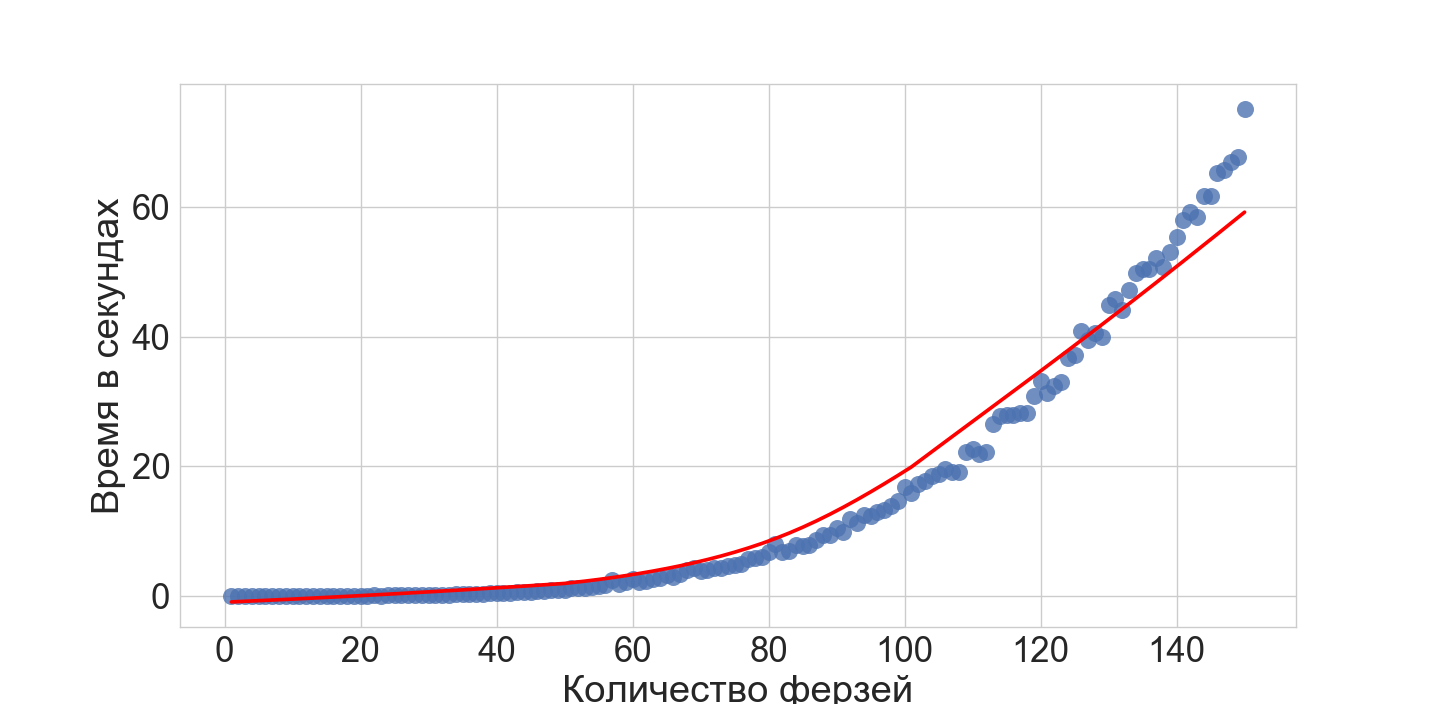
Что куда эффективнее, например, перебора с возвратом.

В качестве общего решения vs специализированный алгоритм

В свой статье Relational Data Factorization (Paramonov, Sergey; van Leeuwen, Matthijs; De Raedt, Luc: Relational data factorization, Machine Learning, volume 106) мы провели очень подробный анализ общего решения одной проблемы, для частного случая которой есть специализированные алгоритмы и в целом картина вот такая:

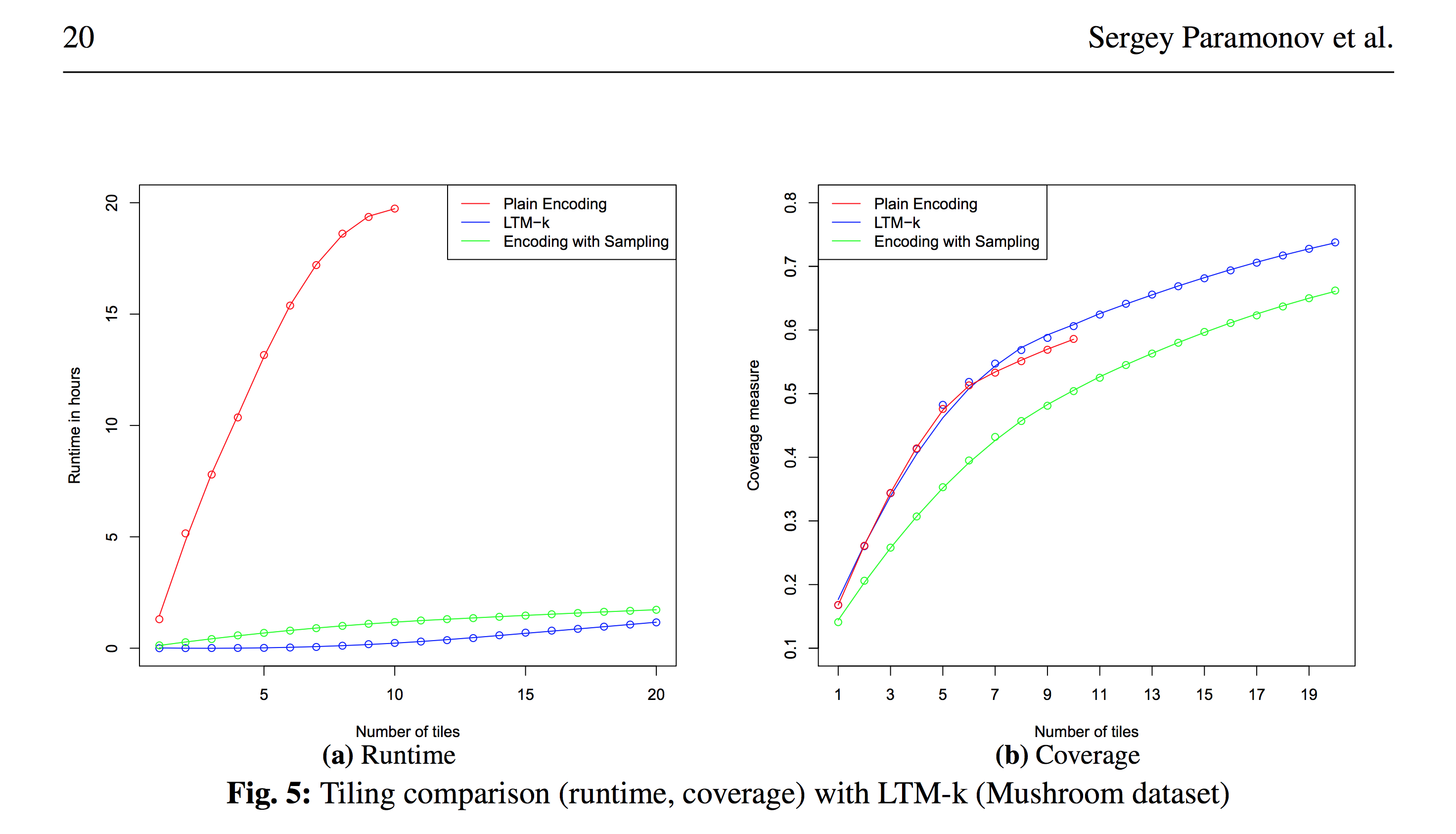
Специализированные алгоритмы существенно быстрее — как мы видим слева по синей и красной кривой (такой специализированный алгоритм + формулировка задачи и тд ~= год труда ученых) при одинаковом качестве — синяя и красная линия справа — однако, в некоторых задачах можно использовать приближенные методы на базе ASP и пожертвовать качеством для получения выигрыша в скорости — зеленая линия.

Гибридные решения

В определенных ситуациях задача может распасться на две части: базовая формулировка задачи + дополнительные ограничения, в такой ситуации можно использовать связку:

Гибридное Решение = Специализированный Алгоритм + ASP

На ряде задач, например в случае с structured frequent pattern mining гибридные решения имеют существенное преимущество в масштабируемости (см. Paramonov, Sergey; Stepanova, Daria; Miettinen, Pauli: Hybrid ASP-based Approach to Pattern Mining, Theory and Practice of Logic Programming, 2018):

Сравнение на синтетическом датасете последовательностей (от авторов другого метода; разница работы на настоящих крупных датасетах несколько порядков — у нас десятки секунды-минуты, у них не получается вычислить все последовательности за ночь вычислений)

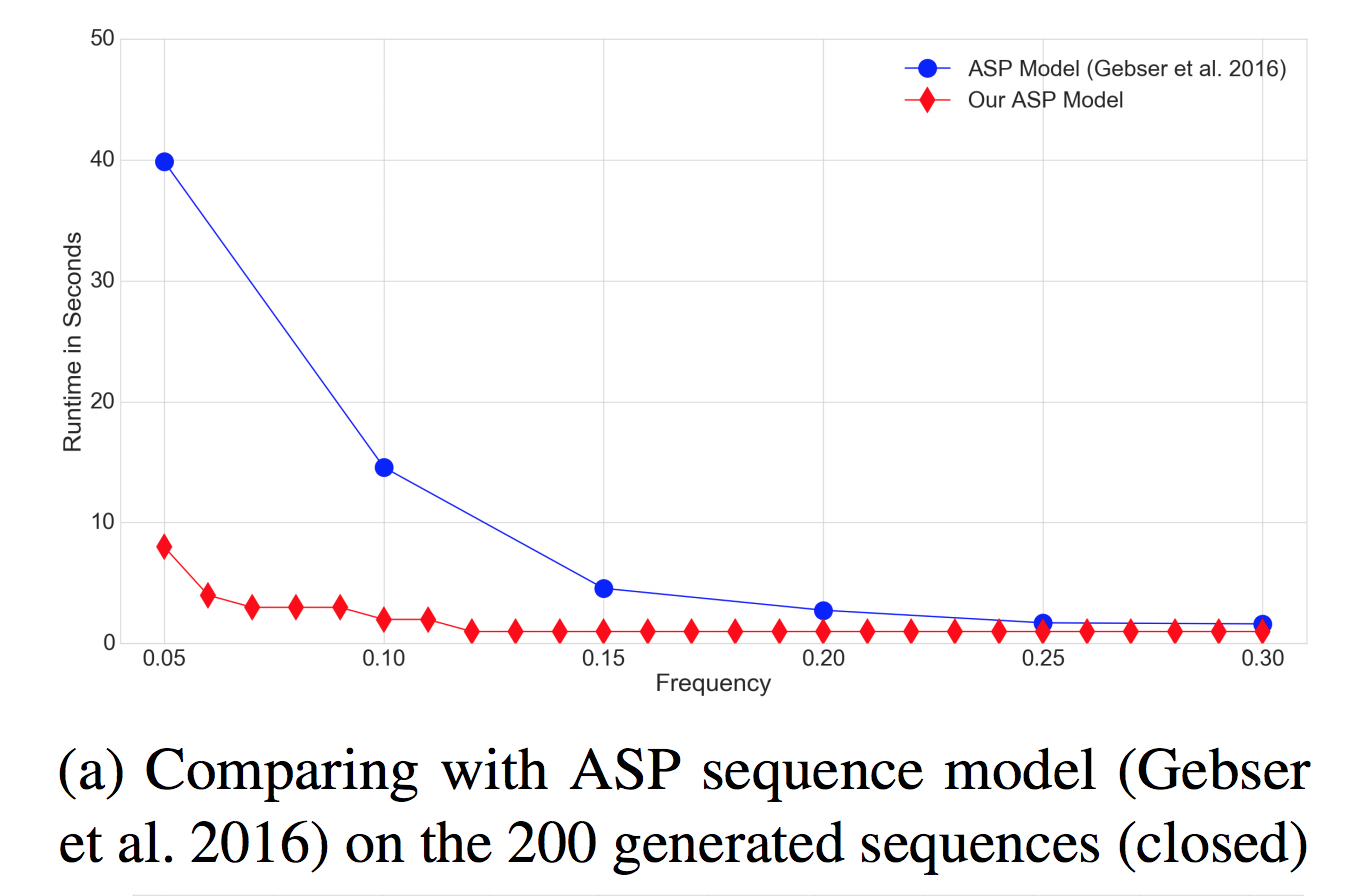
Так же для графовых датасетов разница еще существенней, тут сравнивается старый декларативный метод и новый гибридный (логарифмическая шкала)

Вычисление максимальных часто встречающихся графов

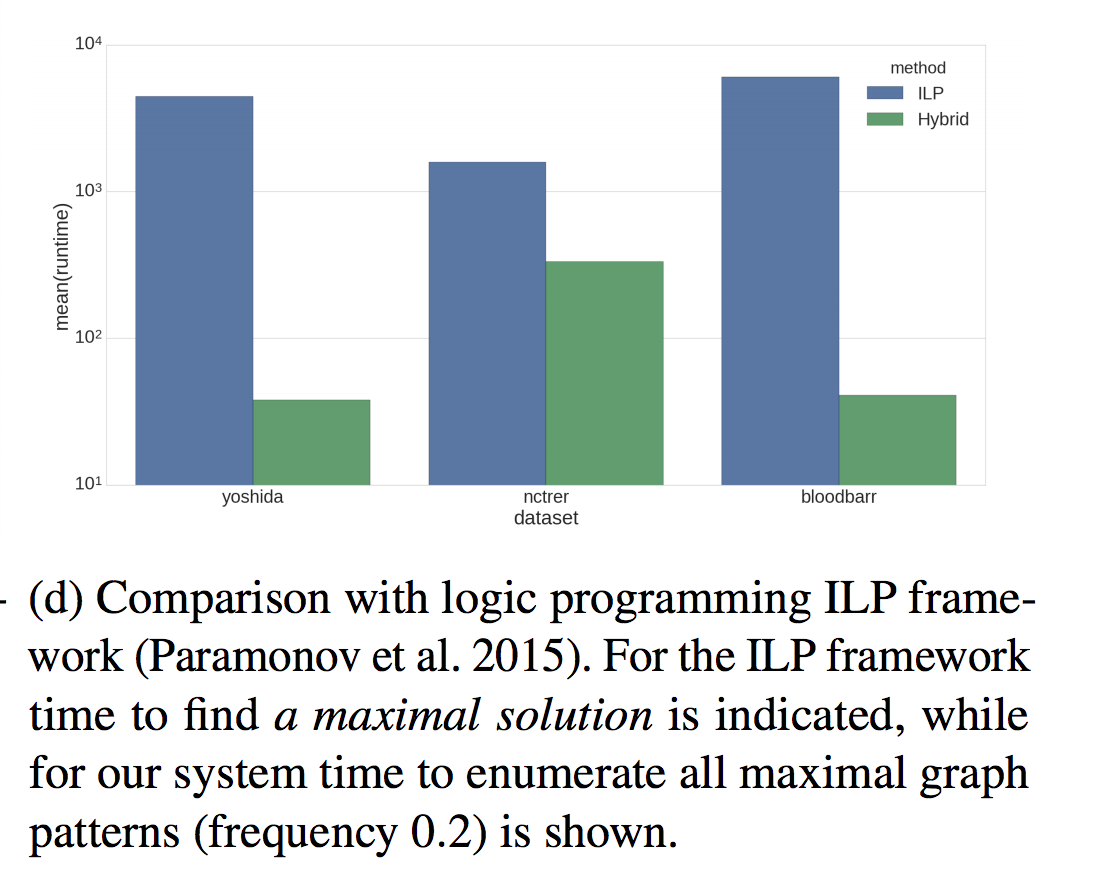
Отсюда следует, что если у нас есть специализированный алгоритм и дополнительные ограничения, то при определенных условиях их можно соединить для более эффективного и общего решения.

Тестирование и корректность программ

Обычно, научные задачи, особенно комбинаторные, сложно отлаживать и еще сложнее показать их корректность. Отсюда возникают подобные проблемы в духе вот таких:

И в целом, если вы думали, что научный код обычно необычайного качества, покрыт тестами и легко поддерживается, то вот кусочек кода из LCM-k:

LCM-k фрагмент кода

Одной из важных особенностей программ с формальной семантикой является доказуемость их корректности, точнее говоря, вы смещаете фокус вопроса корректности на "ASP solver", т.е. систему которая может работать с языком Answer Set Programming. Вы можете показать, что программа и правила математически корректно моделируют вашу задачу — и вопросы по верному выполнению переходят в сообщество разработчиков. У систем, как правило, открытый код — так же они хорошо покрыты тестами и ими пользуются немалая группа юзеров. В среднем, мы достаточно уверены, что с ASP системами все хорошо в плане правильного выполнения кода.

Обычно, когда на свет выходит новый алгоритм (и статья вместе с ним), мы как бы просто верим в часть помеченную "?" на схеме:

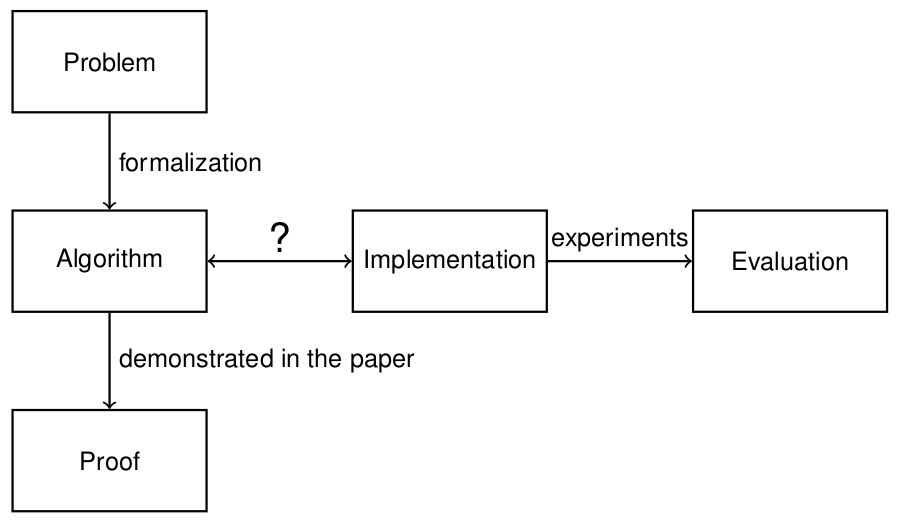
В случае с ASP — algorithm и implementation являются одним и тем же (ну если вы не обернете ASP в процедурные вызовы в алгоритме), а значит можно показать формальную корректность самого кода.

Например, это можно использовать в качестве:

• прототипа решения
• baseline алгоритма
• тестирования более быстрой версии на корректность

Заключение

Сегодня мы многое поняли (с) — и прикоснулись к вершине айсберга логического программирования. Тезисно (tl;dr) статья умещается в несколько пунктов:

• современное логическое программирование != Пролог;
• ASP хорош для решения комбинаторных задач;
• вероятностное логическое программирование подходит для моделей вида: правила + вероятность;
• лучше всего использовать ASP и ЛП для создания прототипов и тестирования идей: "а нам вообще что-то даст это дополнительное ограничение?", "против чего тестировать будем?", etc;
• если у вас нет хороших идей, как написать быстрый поиск к трудной задаче с ограничениями, скорее всего вам пригодится ASP и это будет быстрее и надежнее лобового решения.