Я обнаружил эту закономерность, когда разглядывал пост пользователя xcont. Наткнувшись на эту публикацию, я обратил внимание на то что узоры повторяются не только при увеличении масштаба по числам Фибоначчи.

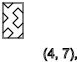
Мне стало интересно есть ли закономерность в этих узорах. Но имея только 2 параметра x и y, я решил что нужно обозначать что-то ещё, общее среди всех получаемых узоров. Тут я заметил что если взять первые 4 квадрата на поле, в любом случае мы получаем 3 варианта начала узора, если линия идёт:
вверх(↑)

вниз(↓)

или же не идёт*(-)

Для обозначения я решил использовать эти символы ↑, ↓, условно называя их спинами (как спин частицы). И вот тут я приступил к созданию таблицы зависимости этих спинов к x,y.
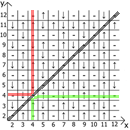
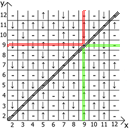
Для начала посмотрим есть ли закономерность если менять только y, x возьмём 4

А теперь о свойствах
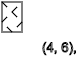
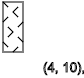
Видим последовательность спинов -↑-↓-↑-↓-↑-↓
Узор повторяется с определённой последовательностью
y=3,7,11...(↑)

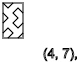
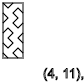
y=5,9,13...(↓)

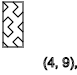

y=2,4,6,8,10,12...(-)



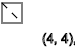

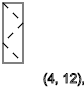
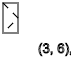
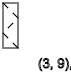
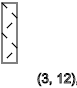
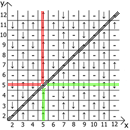
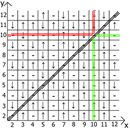
Тоже самое получим если x=3, видим последовательность спинов ↑-↓↑-↓↑-↓↑-↓↑

y=2,5,8,11...(↑)

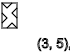
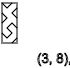
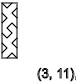
y=4,7,10,13...(↓)

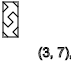
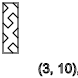
y=3,6,9,12...(-)
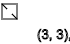



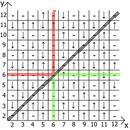
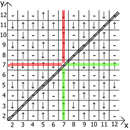
Я подумал что можно систематизировать эти последовательности и составить таблицу этих спинов и вот что я получил.
Представляю вам, «Таблица Чёрного».
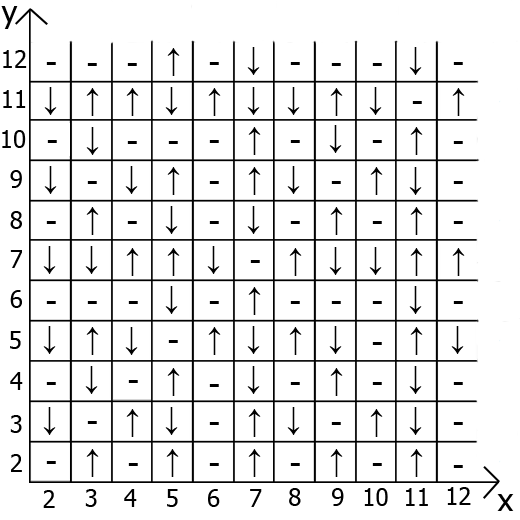
Самое интересное что эта таблица имеет свои зависимости и свойства.
Для начала выведем пару формул:→
если x чётное и y чётное→-, так же если x⋮y или y⋮x→-
x=y→-
x=y+1→↑
x=y-1→↓
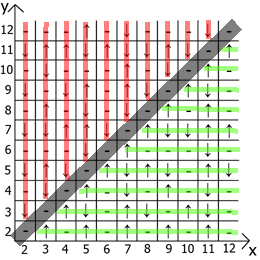
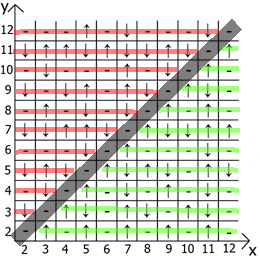
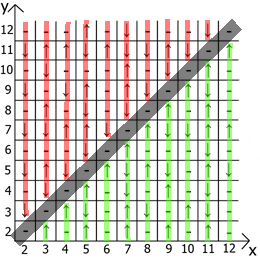
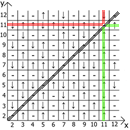
А теперь о свойствах самой таблицы, если взять за точку отсчёта x=y, то в любых направлениях мы имеем зеркально отражённые последовательности(обозначил красными и зелёными линиями).

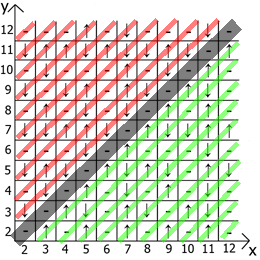
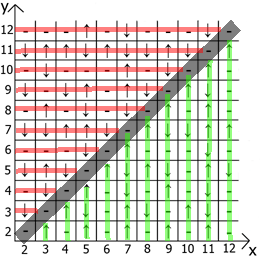
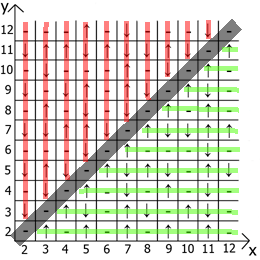
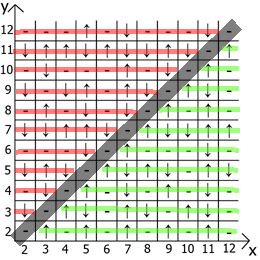
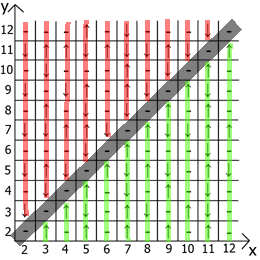




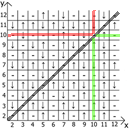

Собственно находите применение и пользуйтесь. Таблица у меня расчерчена до 12 так как изначально всё это я делал на бумаге.

Но при помощи JavaScript алгоритма вы сами можете проверить и более большие значения.
P.S. Не знаю как это можно использовать, но возможно этот алгоритм можно будет применить на квантовом компьютере.
Ссылки: раз и два.

Мне стало интересно есть ли закономерность в этих узорах. Но имея только 2 параметра x и y, я решил что нужно обозначать что-то ещё, общее среди всех получаемых узоров. Тут я заметил что если взять первые 4 квадрата на поле, в любом случае мы получаем 3 варианта начала узора, если линия идёт:
вверх(↑)

вниз(↓)

или же не идёт*(-)

Для обозначения я решил использовать эти символы ↑, ↓, условно называя их спинами (как спин частицы). И вот тут я приступил к созданию таблицы зависимости этих спинов к x,y.
Для начала посмотрим есть ли закономерность если менять только y, x возьмём 4

А теперь о свойствах
Видим последовательность спинов -↑-↓-↑-↓-↑-↓
Узор повторяется с определённой последовательностью
y=3,7,11...(↑)
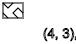
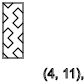
y=5,9,13...(↓)
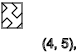
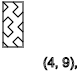
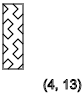
y=2,4,6,8,10,12...(-)
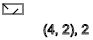
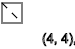
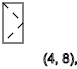
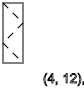
Тоже самое получим если x=3, видим последовательность спинов ↑-↓↑-↓↑-↓↑-↓↑

y=2,5,8,11...(↑)
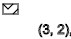
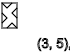
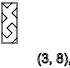
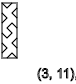
y=4,7,10,13...(↓)

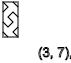
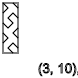
y=3,6,9,12...(-)
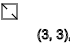
Я подумал что можно систематизировать эти последовательности и составить таблицу этих спинов и вот что я получил.
Представляю вам, «Таблица Чёрного».
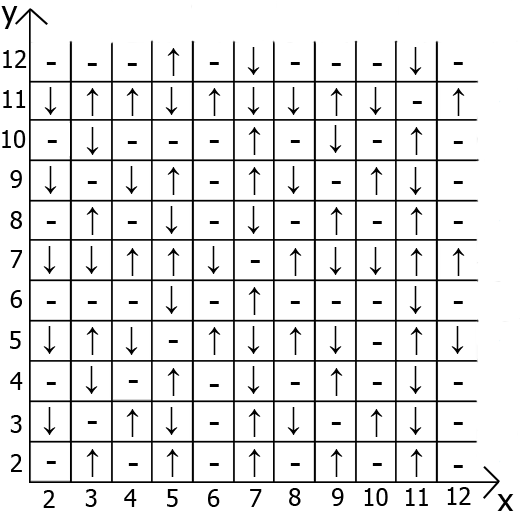
Самое интересное что эта таблица имеет свои зависимости и свойства.
Для начала выведем пару формул:→
если x чётное и y чётное→-, так же если x⋮y или y⋮x→-
x=y→-
x=y+1→↑
x=y-1→↓
А теперь о свойствах самой таблицы, если взять за точку отсчёта x=y, то в любых направлениях мы имеем зеркально отражённые последовательности(обозначил красными и зелёными линиями).
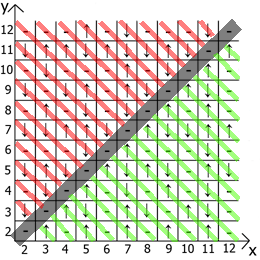
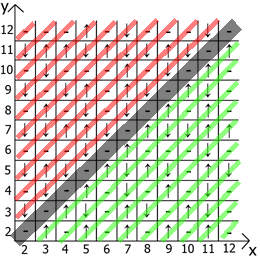
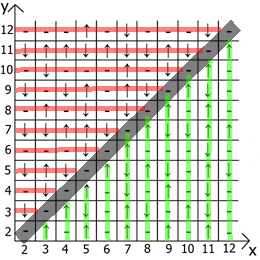

Собственно находите применение и пользуйтесь. Таблица у меня расчерчена до 12 так как изначально всё это я делал на бумаге.

Но при помощи JavaScript алгоритма вы сами можете проверить и более большие значения.
P.S. Не знаю как это можно использовать, но возможно этот алгоритм можно будет применить на квантовом компьютере.
Ссылки: раз и два.






