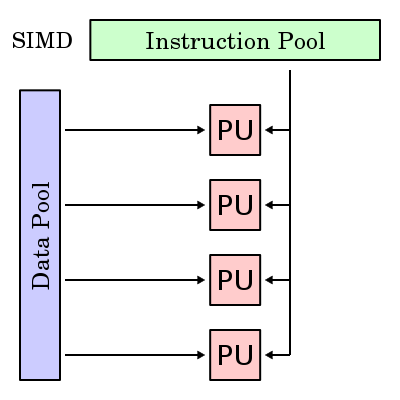
Во время разработки meshoptimizer частенько возникает вопрос: «А может этому алгоритму использовать SIMD?»

Библиотека ориентирована на производительность, но SIMD не всегда обеспечивает значительные преимущества по скорости. К сожалению, SIMD может сделать код менее переносимым и менее ремонтопригодным. Поэтому в каждом конкретном случае приходится искать компромисс. Когда первостепенное значение имеет производительность, приходится разрабатывать и поддерживать отдельные реализации SIMD для наборов инструкций SSE и NEON. В других случаях нужно понять, каков эффект от применения SIMD. Сегодня мы попытаемся ускорить меш-рационализатор (sloppy mesh simplifier) — новый алгоритм, недавно добавленный в библиотеку — используя наборы инструкций SSEn/AVXn.



Для нашего бенчмарка упростим модель Thai Buddha из 6 млн треугольников до 0,1% от этого количества. Используем компилятор Microsoft Visual Studio 2019 для целевой архитектуры x64. Скалярный алгоритм может выполнить такую рационализацию примерно за 210 мс в одном потоке Intel Core i7-8700K (на частоте ~4,4 ГГц). Это соответствует примерно 28,5 млн треугольников в секунду. Возможно, на практике этого достаточно, но мне было любопытно исследовать максимальные возможности оборудования.

В некоторых случаях процедуру можно распараллелить, разделив сетку на куски, но для этого требуется провести дополнительный анализ связности, чтобы сохранить границы, поэтому пока ограничимся чисто SIMD-оптимизациями.

Семь измерений

Чтобы понять возможности для оптимизации, выполним профилирование с помощью Intel VTune. Запустим процедуру 100 раз для гарантии, что данных достаточно.



Здесь я включил режим микроархитектуры, чтобы зафиксировать время выполнения каждой функции, а также найти узкие места. Мы видим, что рационализация выполняется с помощью набора функций, каждая из котоорых требует определённого количества циклов. Список функций отсортирован по времени. Вот они в порядке выполнения, чтобы проще понять алгоритм:

• rescalePositions нормализует позиции всех вершин в единый куб, чтобы подготовиться к квантованию с помощью computeVertexIds
• computeVertexIds вычисляет 30-битный квантованный идентификатор для каждой вершины по равномерной сетке заданного размера, где каждая ось квантуется по сетке (размер сетки 10 бит, так что идентификатор равняется 30)
• countTriangles вычисляет приблизительное количество треугольников, которые создаст рационализатор при заданном размере сетки, предполагая объединение всех вершин в одной ячейке сетки
• fillVertexCells заполняет таблицу, которая соотносит все вершины с соответствующими ячейками; все вершины с одинаковыми ID соотносятся с одной ячейкой
• fillCellQuadrics заполняет структуру Quadric (симметричную матрицу 4×4) для каждой ячейки, чтобы отразить совокупную информацию о соответствующей геометрии
• fillCellRemap вычисляет индекс вершины для каждой ячейки, выбирая одну из вершин в этой ячейке, и минимизирует геометрические искажения
• filterTriangles выводит окончательный набор треугольников в соответствии с таблицами «вершина-ячейка-вершина», построенными ранее; наивная трансляция может производить в среднем ~5% дубликатов треугольников, поэтому функция фильтрует дубликаты.

computeVertexIds и countTriangles выполняются несколько раз: алгоритм определяет размер сетки для слияния вершин, выполняя ускоренный двоичный поиск для достижения целевого количества треугольников (в нашем случае 6000) и вычисляет количество треугольников, которое будет генерировать каждый размер сетки на каждой итерации. Другие функции запускаются однократно. В нашем файле пять поисковых проходов дают целевой размер сетки 40³.

VTune услужливо сообщает, что самая ресурсоёмкая функция — та, что вычисляет квадрики: на неё уходит почти половина общего времени выполнения 21 с. Это первая цель для оптимизации SIMD.

SIMD по кусочкам

Посмотрим на исходный код fillCellQuadrics, чтобы лучше понять, что конкретно она вычисляет:

static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells)
{
    for (size_t i = 0; i < index_count; i += 3)
    {
        unsigned int i0 = indices[i + 0];
        unsigned int i1 = indices[i + 1];
        unsigned int i2 = indices[i + 2];
        unsigned int c0 = vertex_cells[i0];
        unsigned int c1 = vertex_cells[i1];
        unsigned int c2 = vertex_cells[i2];

        bool single_cell = (c0 == c1) & (c0 == c2);
        float weight = single_cell ? 3.f : 1.f;

        Quadric Q;
        quadricFromTriangle(Q,
            vertex_positions[i0],
            vertex_positions[i1],
            vertex_positions[i2],
            weight);

        if (single_cell)
        {
            quadricAdd(cell_quadrics[c0], Q);
        }
        else
        {
            quadricAdd(cell_quadrics[c0], Q);
            quadricAdd(cell_quadrics[c1], Q);
            quadricAdd(cell_quadrics[c2], Q);
        }
    }
}

Функция перебирает все треугольники, вычисляет квадрику для каждого из них и добавляет её в квадрики каждой ячейки. Квадрика — симметричная матрица 4×4, представленная в виде 10 чисел с плавающей запятой:

struct Quadric
{
    float a00;
    float a10, a11;
    float a20, a21, a22;
    float b0, b1, b2, c;
};

Расчёт квадрики требует решения уравнения плоскости для треугольника, построения квадратичной матрицы и взвешивания её, используя площадь треугольника:

static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d)
{
    Q.a00 = a * a;
    Q.a10 = b * a;
    Q.a11 = b * b;
    Q.a20 = c * a;
    Q.a21 = c * b;
    Q.a22 = c * c;
    Q.b0 = d * a;
    Q.b1 = d * b;
    Q.b2 = d * c;
    Q.c = d * d;
}

static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight)
{
    Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z};
    Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z};

    Vector3 normal =
    {
        p10.y * p20.z - p10.z * p20.y,
        p10.z * p20.x - p10.x * p20.z,
        p10.x * p20.y - p10.y * p20.x
    };
    float area = normalize(normal);

    float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z;

    quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance);

    quadricMul(Q, area * weight);
}

Похоже, здесь много операций с плавающей запятой, так что их можно распараллелить с помощью SIMD. Для начала представим каждый вектор в виде 4-wide вектора SIMD, и также изменим структуру Quadric на 12 чисел с плавающей запятой вместо 10, чтобы она ровно укладывалась в три регистра SIMD (увеличение размера не отражается на производительности) и изменим порядок полей, чтобы вычисления в quadricFromPlane стали более равномерными:

struct Quadric
{
    float a00, a11, a22;
    float pad0;
    float a10, a21, a20;
    float pad1;
    float b0, b1, b2, c;
};

Здесь некоторые вычисления, в частности, скалярное произведение, не очень соответствуют более ранним версиям SSE. К счастью, в SSE4.1 появилась инструкция для скалярного произведения, что нам весьма кстати.

static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells)
{
    const int yzx = _MM_SHUFFLE(3, 0, 2, 1);
    const int zxy = _MM_SHUFFLE(3, 1, 0, 2);
    const int dp_xyz = 0x7f;

    for (size_t i = 0; i < index_count; i += 3)
    {
        unsigned int i0 = indices[i + 0];
        unsigned int i1 = indices[i + 1];
        unsigned int i2 = indices[i + 2];
        unsigned int c0 = vertex_cells[i0];
        unsigned int c1 = vertex_cells[i1];
        unsigned int c2 = vertex_cells[i2];

        bool single_cell = (c0 == c1) & (c0 == c2);

        __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x);
        __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x);
        __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x);

        __m128 p10 = _mm_sub_ps(p1, p0);
        __m128 p20 = _mm_sub_ps(p2, p0);

        __m128 normal = _mm_sub_ps(
            _mm_mul_ps(
                _mm_shuffle_ps(p10, p10, yzx),
                _mm_shuffle_ps(p20, p20, zxy)),
            _mm_mul_ps(
                _mm_shuffle_ps(p10, p10, zxy),
                _mm_shuffle_ps(p20, p20, yzx)));

        __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz); // SSE4.1
        __m128 area = _mm_sqrt_ps(areasq);

        // masks the result of the division when area==0
        // scalar version does this in normalize()
        normal = _mm_and_ps(
            _mm_div_ps(normal, area),
            _mm_cmpneq_ps(area, _mm_setzero_ps()));

        __m128 distance = _mm_dp_ps(normal, p0, dp_xyz); // SSE4.1
        __m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance);
        __m128 normalnegdist = _mm_blend_ps(normal, negdistance, 8);

        __m128 Qx = _mm_mul_ps(normal, normal);
        __m128 Qy = _mm_mul_ps(
            _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)),
            _mm_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0)));
        __m128 Qz = _mm_mul_ps(negdistance, normalnegdist);

        if (single_cell)
        {
            area = _mm_mul_ps(area, _mm_set1_ps(3.f));
            Qx = _mm_mul_ps(Qx, area);
            Qy = _mm_mul_ps(Qy, area);
            Qz = _mm_mul_ps(Qz, area);

            Quadric& q0 = cell_quadrics[c0];

            __m128 q0x = _mm_loadu_ps(&q0.a00);
            __m128 q0y = _mm_loadu_ps(&q0.a10);
            __m128 q0z = _mm_loadu_ps(&q0.b0);

            _mm_storeu_ps(&q0.a00, _mm_add_ps(q0x, Qx));
            _mm_storeu_ps(&q0.a10, _mm_add_ps(q0y, Qy));
            _mm_storeu_ps(&q0.b0, _mm_add_ps(q0z, Qz));
        }
        else
        {
            // omitted for brevity, repeats the if() body
            // three times for c0/c1/c2
        }
    }
}

В этом коде ничего особо интересного; мы здесь обильно используем невыровненные инструкции load/store. Хотя входные данные Vector3 можно и выровнять, но здесь, кажется, нет заметного штрафа за невыровненные чтения. Обратите внимание, что в первой половине функции не используются векторы, что и хорошо — у наших векторов три компонента, а в некоторых случаях только один (см. вычисление areasq/area/distance), в то время как процессор выполняет параллельно 4 операции. В любом случае, давайте посмотрим, насколько помогла параллелизация.



Сотня запусков fillCellQuadrics теперь выполняется за 5,3 с вместо 9,8 с, что экономит примерно 45 мс на каждой операции — неплохо, но не очень впечатляет. Во многих инструкциях мы используем три вместо четырёх компонентов, а также точеное умножение, что даёт довольно значительную задержку. Если вы раньше писали инструкции для SIMD, то знаете, как правильно делать скалярное произведение.

Для этого нужно делать сразу четыре вектора. Вместо того, чтобы хранить один полный вектор в одном регистре SIMD, мы используем три регистра — в одном храним четыре компонента x, в другом будет храниться у, а в третьем z. Здесь для работы нужны сразу четыре вектора: значит, будем обрабатывать одновременно четыре треугольника.

У нас много массивов с динамической индексацией. Обычно она помогает предварительно перенести данные в подготовленные массивы компонентов x/y/z (вернее, обычно используются небольшие SIMD-регистры, например, float x[8], y[8], z[8], для каждой из 8 вершин во входных данных: это называется AoSoA (массивы структур массивов) и даёт хороший баланс между локальностью кэша и простотой загрузки в SIMD-регистры), но здесь динамическая индексация не очень хорошо сработает, поэтому загрузим данные для четырёх треугольников как обычно, и транспонируем векторы с помощью удобного макроса _MM_TRANSPOSE.

Теоретически, нужно вычислить каждый компонент четырёх конечных квадрик в собственном регистре SIMD (например, у нас будет __m128 Q_a00 с четырьмя составляющими a00 конечных квадрик). В этом случае операции над квадриками довольно хорошо укладываются в 4-wide инструкции SIMD, а преобразование фактически замедляет код — поэтому мы транспонируем только начальные векторы, а затем транспонируем обратно уравнения плоскости и запускаем тот же код, который использовали для вычисления квадрик, но повторяем его четыре раза. Вот как выглядит код, который затем вычисляет уравнения плоскости (остальные части для краткости опущены):

unsigned int i00 = indices[(i + 0) * 3 + 0];
unsigned int i01 = indices[(i + 0) * 3 + 1];
unsigned int i02 = indices[(i + 0) * 3 + 2];
unsigned int i10 = indices[(i + 1) * 3 + 0];
unsigned int i11 = indices[(i + 1) * 3 + 1];
unsigned int i12 = indices[(i + 1) * 3 + 2];
unsigned int i20 = indices[(i + 2) * 3 + 0];
unsigned int i21 = indices[(i + 2) * 3 + 1];
unsigned int i22 = indices[(i + 2) * 3 + 2];
unsigned int i30 = indices[(i + 3) * 3 + 0];
unsigned int i31 = indices[(i + 3) * 3 + 1];
unsigned int i32 = indices[(i + 3) * 3 + 2];

// load first vertex of each triangle and transpose into vectors with components (pw0 isn't used later)
__m128 px0 = _mm_loadu_ps(&vertex_positions[i00].x);
__m128 py0 = _mm_loadu_ps(&vertex_positions[i10].x);
__m128 pz0 = _mm_loadu_ps(&vertex_positions[i20].x);
__m128 pw0 = _mm_loadu_ps(&vertex_positions[i30].x);
_MM_TRANSPOSE4_PS(px0, py0, pz0, pw0);

// load second vertex of each triangle and transpose into vectors with components
__m128 px1 = _mm_loadu_ps(&vertex_positions[i01].x);
__m128 py1 = _mm_loadu_ps(&vertex_positions[i11].x);
__m128 pz1 = _mm_loadu_ps(&vertex_positions[i21].x);
__m128 pw1 = _mm_loadu_ps(&vertex_positions[i31].x);
_MM_TRANSPOSE4_PS(px1, py1, pz1, pw1);

// load third vertex of each triangle and transpose into vectors with components
__m128 px2 = _mm_loadu_ps(&vertex_positions[i02].x);
__m128 py2 = _mm_loadu_ps(&vertex_positions[i12].x);
__m128 pz2 = _mm_loadu_ps(&vertex_positions[i22].x);
__m128 pw2 = _mm_loadu_ps(&vertex_positions[i32].x);
_MM_TRANSPOSE4_PS(px2, py2, pz2, pw2);

// p1 - p0
__m128 px10 = _mm_sub_ps(px1, px0);
__m128 py10 = _mm_sub_ps(py1, py0);
__m128 pz10 = _mm_sub_ps(pz1, pz0);

// p2 - p0
__m128 px20 = _mm_sub_ps(px2, px0);
__m128 py20 = _mm_sub_ps(py2, py0);
__m128 pz20 = _mm_sub_ps(pz2, pz0);

// cross(p10, p20)
__m128 normalx = _mm_sub_ps(
    _mm_mul_ps(py10, pz20),
    _mm_mul_ps(pz10, py20));
__m128 normaly = _mm_sub_ps(
    _mm_mul_ps(pz10, px20),
    _mm_mul_ps(px10, pz20));
__m128 normalz = _mm_sub_ps(
    _mm_mul_ps(px10, py20),
    _mm_mul_ps(py10, px20));

// normalize; note that areasq/area now contain 4 values, not just one
__m128 areasq = _mm_add_ps(
    _mm_mul_ps(normalx, normalx),
    _mm_add_ps(
        _mm_mul_ps(normaly, normaly),
        _mm_mul_ps(normalz, normalz)));
__m128 area = _mm_sqrt_ps(areasq);
__m128 areanz = _mm_cmpneq_ps(area, _mm_setzero_ps());

normalx = _mm_and_ps(_mm_div_ps(normalx, area), areanz);
normaly = _mm_and_ps(_mm_div_ps(normaly, area), areanz);
normalz = _mm_and_ps(_mm_div_ps(normalz, area), areanz);

__m128 distance = _mm_add_ps(
    _mm_mul_ps(normalx, px0),
    _mm_add_ps(
        _mm_mul_ps(normaly, py0),
        _mm_mul_ps(normalz, pz0)));
__m128 negdistance = _mm_sub_ps(_mm_setzero_ps(), distance);

// this computes the plane equations (a, b, c, d) for each of the 4 triangles
__m128 plane0 = normalx;
__m128 plane1 = normaly;
__m128 plane2 = normalz;
__m128 plane3 = negdistance;
_MM_TRANSPOSE4_PS(plane0, plane1, plane2, plane3);

Код стал немного длиннее: теперь мы обрабатываем по четыре треугольника в каждой итерации, и нам больше не нужны для этого инструкции SSE4.1. По идее, юниты SIMD должны использоваться эффективнее. Посмотрим, насколько это помогло.



Ну ладно, ничего страшного. Код ускорился очень незначительно, хотя функция fillCellQuadrics теперь выполняется почти вдвое быстрее по сравнению с первоначальной функцией без SIMD, но неясно, оправдывает ли это значительное увеличение сложности. Теоретически, можно использовать AVX2 и обрабатывать 8 треугольников на итерацию, но здесь понадобится ещё сильнее раскручивать цикл вручную (в идеале весь этот код генерируется с помощью ISPC, но мои наивные попытки заставить его генерировать хороший код не привели к успеху: вместо последовательностей load/store он настойчиво выдавал gather/scatter, что значительно замедляет выполнение). Попробуем что-нибудь другое.

AVX2 = SSE2 + SSE2

AVX2 — немного своеобразный набор инструкций. У него 8-wide регистры с плавающей запятой, а одной инструкцией можно выполнить 8 операций; но по сути такая инструкция не отличается от двух инструкций SSE2, выполняемых на двух половинах регистра (насколько я понимаю, первые процессоры с поддержкой AVX2 декодировали каждую инструкцию в две или более микроопераций, поэтому прирост производительности был ограничен фазой извлечения инструкций). Например, _mm_dp_ps осуществляет скалярное произведение между двумя регистрами SSE2, а _mm256_dp_ps производит два скалярных произведения между двумя половинами двух регистров AVX2, поэтому ограничена 4-wide для каждой половины.

Из-за этого код AVX2 часто отличается от универсального “8-wide SIMD”, но здесь это работает в нашу пользу: вместо попыток улучшить векторизацию путём транспонирования 4-wide векторов вернёмся к первому варианту SIMD и раскрутим цикл вдвое, используя инструкции AVX2 вместо SSE2/SSE4. Нам по-прежнему нужно загружать и хранить векторы 4-wide, но в целом просто меняем в коде __m128 на __m256 и _mm_ на _mm256 с несколькими настройками:

unsigned int i00 = indices[(i + 0) * 3 + 0];
unsigned int i01 = indices[(i + 0) * 3 + 1];
unsigned int i02 = indices[(i + 0) * 3 + 2];
unsigned int i10 = indices[(i + 1) * 3 + 0];
unsigned int i11 = indices[(i + 1) * 3 + 1];
unsigned int i12 = indices[(i + 1) * 3 + 2];

__m256 p0 = _mm256_loadu2_m128(
    &vertex_positions[i10].x,
    &vertex_positions[i00].x);
__m256 p1 = _mm256_loadu2_m128(
    &vertex_positions[i11].x,
    &vertex_positions[i01].x);
__m256 p2 = _mm256_loadu2_m128(
    &vertex_positions[i12].x,
    &vertex_positions[i02].x);

__m256 p10 = _mm256_sub_ps(p1, p0);
__m256 p20 = _mm256_sub_ps(p2, p0);

__m256 normal = _mm256_sub_ps(
    _mm256_mul_ps(
        _mm256_shuffle_ps(p10, p10, yzx),
        _mm256_shuffle_ps(p20, p20, zxy)),
    _mm256_mul_ps(
        _mm256_shuffle_ps(p10, p10, zxy),
        _mm256_shuffle_ps(p20, p20, yzx)));

__m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz);
__m256 area = _mm256_sqrt_ps(areasq);
__m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ);

normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz);

__m256 distance = _mm256_dp_ps(normal, p0, dp_xyz);
__m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance);
__m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88);

__m256 Qx = _mm256_mul_ps(normal, normal);
__m256 Qy = _mm256_mul_ps(
    _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)),
    _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0)));
__m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);

Тут можно взять каждую 128-битную половину полученных векторов Qx/Qy/Qz и запустить тот же код, который мы использовали для сложения квадрик. Вместо этого мы предполагаем, что если у треугольника три вершины в одной ячейке (значение single_cell == true), то очень вероятно, что у другого треугольника тоже три вершины в другой ячейке, и производим окончательное агрегирование квадрик также с помощью AVX2:

unsigned int c00 = vertex_cells[i00];
unsigned int c01 = vertex_cells[i01];
unsigned int c02 = vertex_cells[i02];
unsigned int c10 = vertex_cells[i10];
unsigned int c11 = vertex_cells[i11];
unsigned int c12 = vertex_cells[i12];

bool single_cell =
    (c00 == c01) & (c00 == c02) &
    (c10 == c11) & (c10 == c12);

if (single_cell)
{
    area = _mm256_mul_ps(area, _mm256_set1_ps(3.f));
    Qx = _mm256_mul_ps(Qx, area);
    Qy = _mm256_mul_ps(Qy, area);
    Qz = _mm256_mul_ps(Qz, area);

    Quadric& q00 = cell_quadrics[c00];
    Quadric& q10 = cell_quadrics[c10];

    __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00);
    __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10);
    __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0);

    _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx));
    _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy));
    _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz));
}
else
{
    // omitted for brevity
}

Полученный код проще, лаконичнее и быстрее, чем наш неудачный подход SSE2:



Конечно, мы не добились ускорения в 8 раз, а всего в 2,45 раза. Операции загрузки и хранения по-прежнему 4-wide, так как мы вынуждены работать с неудобной компоновкой памяти из-за динамического индексирования, а вычисления не являются оптимальными для SIMD. Но теперь fillCellQuadrics больше не является узким местом в конвейере нашего профиля, и можно сосредоточиться на других функциях.

Соберитесь вокруг, дети

Мы сэкономили 4,8 секунды на тестовом прогоне (48 мс на каждом запуске), и теперь наш главный нарушитель — countTriangles. Казалось бы, простая функция, но она выполняется не один, а пять раз:

static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count)
{
    size_t result = 0;

    for (size_t i = 0; i < index_count; i += 3)
    {
        unsigned int id0 = vertex_ids[indices[i + 0]];
        unsigned int id1 = vertex_ids[indices[i + 1]];
        unsigned int id2 = vertex_ids[indices[i + 2]];

        result += (id0 != id1) & (id0 != id2) & (id1 != id2);
    }

    return result;
}

Функция перебирает все исходные треугольники и вычисляет число невырожденных треугольников, сравнивая идентификаторы вершин. Не сразу понятно, как её распараллелить с помощью SIMD… если только вы не используете инструкции gather.

Набор инструкций AVX2 добавил в x64 SIMD семейство инструкций gather/scatter; каждая из них принимает векторный регистр с 4 или 8 значениями — и одновременно выполняет 4 или 8 операции загрузки или сохранения. Если здесь использовать gather, то можно загрузить три индекса, выполнить gather по всем сразу (или в группах по 4 или 8) и сравнить результаты. Gather на процессорах Intel исторически работает довольно медленно, но давайте попробуем. Для простоты загрузим данные для 8 треугольников, транспонируем векторы аналогично нашей предыдущей попытке и проведём сравнение соответствующих элементов каждого вектора:

for (size_t i = 0; i < (triangle_count & ~7); i += 8)
{
    __m256 tri0 = _mm256_loadu2_m128(
        (const float*)&indices[(i + 4) * 3 + 0],
        (const float*)&indices[(i + 0) * 3 + 0]);
    __m256 tri1 = _mm256_loadu2_m128(
        (const float*)&indices[(i + 5) * 3 + 0],
        (const float*)&indices[(i + 1) * 3 + 0]);
    __m256 tri2 = _mm256_loadu2_m128(
        (const float*)&indices[(i + 6) * 3 + 0],
        (const float*)&indices[(i + 2) * 3 + 0]);
    __m256 tri3 = _mm256_loadu2_m128(
        (const float*)&indices[(i + 7) * 3 + 0],
        (const float*)&indices[(i + 3) * 3 + 0]);

    _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3);

    __m256i i0 = _mm256_castps_si256(tri0);
    __m256i i1 = _mm256_castps_si256(tri1);
    __m256i i2 = _mm256_castps_si256(tri2);

    __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4);
    __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4);
    __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4);

    __m256i deg = _mm256_or_si256(
        _mm256_cmpeq_epi32(id1, id2),
        _mm256_or_si256(
            _mm256_cmpeq_epi32(id0, id1),
            _mm256_cmpeq_epi32(id0, id2)));

    result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4;
}

Макрос _MM_TRANSPOSE8_LANE4_PS в AVX2 является эквивалентом _MM_TRANSPOSE4_PS, который отсутствует в стандартном заголовке, но легко выводится. Он принимает четыре вектора AVX2 и транспонирует две матрицы 4×4 независимо друг от друга:

#define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \
do { \
    __m256 __t0, __t1, __t2, __t3; \
    __t0 = _mm256_unpacklo_ps(row0, row1); \
    __t1 = _mm256_unpackhi_ps(row0, row1); \
    __t2 = _mm256_unpacklo_ps(row2, row3); \
    __t3 = _mm256_unpackhi_ps(row2, row3); \
    row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \
    row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \
    row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \
    row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \
} while (0)

Из-за некоторых особенностей в наборах инструкций SSE2/AVX2 мы должны при транспонировании векторов использовать операции регистра с плавающей запятой. Мы тут загружаем данные немного небрежно; но это в основном не имеет значения, потому что нас ограничивает производительность gather:



Теперь countTriangles работает примерно на 27% быстрее, и обратите внимание на ужасный показатель CPI (циклов на инструкцию): мы отправляем примерно вчетверо меньше инструкций, но gather занимает много времени. Здорово, что он ускоряет общую работу, но, конечно, прирост производительности несколько удручает. Нам удалось обогнать fillCellQuadrics в профиле, что подводит нас к последней функции вверху списка, на которую мы ещё не смотрели.

Глава 6, где всё начинает работать как надо

Последняя функция — это computeVertexIds. В алгоритме она выполняется 6 раз, поэтому тоже представляет собой отличную цель для оптимизации. Впервые мы видим функцию, которая словно создана для чёткой оптимизации в SIMD:

static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size)
{
    assert(grid_size >= 1 && grid_size <= 1024);
    float cell_scale = float(grid_size - 1);

    for (size_t i = 0; i < vertex_count; ++i)
    {
        const Vector3& v = vertex_positions[i];

        int xi = int(v.x * cell_scale + 0.5f);
        int yi = int(v.y * cell_scale + 0.5f);
        int zi = int(v.z * cell_scale + 0.5f);

        vertex_ids[i] = (xi << 20) | (yi << 10) | zi;
    }
}

После предыдущих оптимизаций мы знаем, что нужно делать: раскрутить цикл 4 или 8 раз, так как нет никакого смысла пытаться ускорить только одну итерацию, транспонировать векторные компоненты и запустить вычисления параллельно. Сделаем это с помощью AVX2, обрабатывая по 8 вершин за раз:

__m256 scale = _mm256_set1_ps(cell_scale);
__m256 half = _mm256_set1_ps(0.5f);

for (size_t i = 0; i < (vertex_count & ~7); i += 8)
{
    __m256 vx = _mm256_loadu2_m128(
        &vertex_positions[i + 4].x,
        &vertex_positions[i + 0].x);
    __m256 vy = _mm256_loadu2_m128(
        &vertex_positions[i + 5].x,
        &vertex_positions[i + 1].x);
    __m256 vz = _mm256_loadu2_m128(
        &vertex_positions[i + 6].x,
        &vertex_positions[i + 2].x);
    __m256 vw = _mm256_loadu2_m128(
        &vertex_positions[i + 7].x,
        &vertex_positions[i + 3].x);

    _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw);

    __m256i xi = _mm256_cvttps_epi32(
        _mm256_add_ps(_mm256_mul_ps(vx, scale), half));
    __m256i yi = _mm256_cvttps_epi32(
        _mm256_add_ps(_mm256_mul_ps(vy, scale), half));
    __m256i zi = _mm256_cvttps_epi32(
        _mm256_add_ps(_mm256_mul_ps(vz, scale), half));

    __m256i id = _mm256_or_si256(
        zi,
        _mm256_or_si256(
            _mm256_slli_epi32(xi, 20),
            _mm256_slli_epi32(yi, 10)));

    _mm256_storeu_si256((__m256i*)&vertex_ids[i], id);
}

И посмотрим на результаты:



Мы ускорили computeVertexIds в два раза. С учётом всех оптимизаций общее время выполнения программы сократилось примерно до 120 мс, что соответствует обсчёту 50 млн. треугольников в секунду.

Может показаться, что мы опять не добились ожидаемого роста производительности: разве computeVertexIds не должен ускориться больше чем в два раза после распараллеливания? Чтобы ответить на этот вопрос, попробуем посмотреть, сколько работы выполняет эта функция.

computeVertexIds выполняется шесть раз на один запуск программы: пять раз во время двоичного поиска и один раз в конце для вычисления окончательных идентификаторов, которые используются для дальнейшей обработки. Каждый раз эта функция обрабатывает 3 млн вершин, считывая 12 байт для каждой вершины и записывая 4 байта.

В общей сложности за 100 прогонов рационализатора эта функция обрабатывает 1,8 млрд вершин, считывая 21 ГБ и записывая обратно 7 ГБ. Обработка 28 ГБ за 1,46 секунды требует пропускной способности шины 19 ГБ/с. Мы можем проверить пропускную способность памяти, запустив memcmp(block1, block2, 512 MB). Результат — 45 мс, то есть около 22 ГБ/с на одном ядре (хотя бенчмарк AIDA64 показывает скорость чтения на моей системе до 31 ГБ/с, но он использует несколько ядер). По сути, мы приблизились максимально достижимому лимиту памяти, и дальнейшее повышение производительности потребует более плотной упаковки данных вершин, чтобы они занимали менее 12 байт.

Заключение

Мы взяли довольно хорошо оптимизированный алгоритм, который упрощает очень большие сетки со скоростью 28 миллионов треугольников в секунду, и использовали наборы инструкций SSE и AVX, чтобы ускорить его почти в два раза, до 50 миллионов треугольников в секунду. Во время этого путешествия нам пришлось изучить различные способы применения SIMD: регистры для хранения 3-wide векторов, SoA-транспонирование, AVX2-инструкции для хранения двух 3-wide векторов, инструкции gather для ускорения загрузки данных по сравнению со скалярными инструкциями и, наконец, мы напрямую применили AVX2 для потоковой обработки.

Зачастую SIMD не лучшая отправная точка для оптимизации: меш-рационализатор прошёл через много итераций алгоритмической оптимизации и микрооптимизации без использования специфичных для платформы инструкций. Но в какой-то момент эти возможности исчерпываются, и если производительность критична, то SIMD — фантастический инструмент, который можно использовать при необходимости.

Не уверен, какие из этих оптимизаций попадут в основную ветку meshoptimizer: в конце концов, это лишь эксперимент, чтобы увидеть, насколько разгоняется код без кардинального изменения алгоритмов. Надеюсь, статья оказалась информативной и даст вам идеи по оптимизации кода. Окончательные исходники для этой статьи лежат здесь; эта работа основана на версии meshoptimizer 99ab49, а модель Thai Buddha опубликована на Sketchfab.