Часть I
Часть II
В данной статье рассматривается метод оценок диапазона принимаемых значений и связь этого метода с задачами, содержащими модуль.
При решении некоторых задач необходимо рассматривать диапазон, в пределах которого может находиться искомая величина.
Рассмотрим метод оценок при решении неравенств.
Дать оценку сверху означает определить максимальное значение, которое может принимать искомая величина.
Предположим, что цена за одну единицу товара может колебаться в пределах от 5 до 10 RUB. Для двух единиц товара оценка сверху составляет 10+10=20 RUB, оценка снизу 5+5=10 RUB.
Рассмотрим задачу из задачника профильной направленности М.И. Башмакова
37. Известны оценки для переменных и
и 
Дайте оценки сверху для следующих выражений:
1.
2.
5.
6.
8.
9.
Вообще, анализ бесконечно малых величин использует критерий оценки. А модуль (как окрестность) присутствует в самом определении предела последовательности.
Определение эпсилон-окресности на примере радиоактивонго распада приводится в учебнике «Математический анализ. Учебное пособие для IX — X классов»
Вернёмся к задаче
38. Вычислить сумму
Ряд ограничен сверху. К вопросу о верних и нижних оценках вернёмся после.
ограничен сверху. К вопросу о верних и нижних оценках вернёмся после.
Отбросим первое слагаемое и рассчитаем, чему равен остаток ряда после первого члена
и рассчитаем, чему равен остаток ряда после первого члена
Получим
Отбросим первое и второе слагаемые и рассмотрим остаток ряда.
Получим 0.33333233333632745
Если ряд сходится, то сумма его остатка после m-го члена с возрастанием m стремится к нулю.
У нас сумма остатка с возрастанием m стремится к нулю.
Рассмотрим пример из «Курса дифференциального и интегрального исчисления» 363(6)
 действительно больше
действительно больше  , нужно произвести оценку снизу данного выражения. Получим систему неравенств
, нужно произвести оценку снизу данного выражения. Получим систему неравенств
Произведя сложение всех неравенств данной системы, получим
Следовательно, данный ряд расходится.
Для гармонического ряда этот метод не проходит, потому что -я частичная сумма гармонического ряда
-я частичная сумма гармонического ряда
Подсчитаем частичные суммы, которые получаются при отбрасывании слагаемых.
слагаемых.
Данный рекурсивный алгоритм вызывает быстрое переполнение стека.
В этой статье есть пример вычисления факториала с помощью итеративного алгоритма. Изменим этот итеративный алгоритм так, чтобы он вычислял частичную сумму Hn внутри определённых границ; назовём эти границы a и b
Нижней границей является число , верхней границей — число
, верхней границей — число 
Напишем функцию, вычисляющую степень двойки
Будем в качестве нижней границы подставлять (+ 1 (power_of_two k)), а в качестве верхней можно использовать функцию (* 2 (power_of_two k)) или эквивалентную ей функцию (power_of_two (+ 1 k))
Перепишем функцию Hn
Теперь можно вычислять Hn при больших значениях .
.
Напишем на языке Си программу, которая замеряет время, необходимое на вычисление Hn. Будем использовать функцию clock() из стандартной библиотеки <time.h>
Статья про измерение процессорного времени есть на Хабре здесь.
Обычно online ide ограничивают время выполнения запускаемых программ пятью секундами, поэтому эту программу можно проверить лишь в некоторых online ide, например, в onlinegdb.com или repl.it
При k от 1+2^30 до 2^31 время работы составит ~5 сек.
При k от 1+2^31 до 2^32 время работы составит ~10 сек.
При k от 1+2^32 до 2^33 время работы составит ~20 сек.
При k от 1+2^33 до 2^34 время работы составит ~40 сек.
При k от 1+2^34 до 2^35 время работы составит больше одной минуты.
…
При k от 1+2^45 до 2^46 время работы составит больше 24 часов.
Предположим, что для k от 1+2^30 до 2^31 время выполнения алгоритма составляет ~2 сек.
Тогда для k=2^(30+n) время выполнения алгоритма составляет 2^n сек. (при )
)
Данный алгоритм имеет экспотенциальную сложность.
Вернёмся к модулям.
В интегральном исчислении модуль используется в формуле
Читайте также Самый натуральный логарифм.
Присутствие модуля в формуле обосновывается далее в «Курсе дифференциального и интегрального исчисления»
обосновывается далее в «Курсе дифференциального и интегрального исчисления»
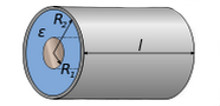
Физическое приложение интеграла
Этот интеграл используется для вычисления разности потенциалов обкладок цилиндрического конденсатора.
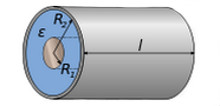
«Электричество и магнетизм»:
 , потому что
, потому что  и
и  строго положительны и такая форма записи является избыточной.
строго положительны и такая форма записи является избыточной.
С помощью модулей можно рисовать различные фигуры.
Если в программе geogebra написать формулу получим
получим

Можно рисовать более сложные фигуры. Нарисуем, например, «бабочку» в облаке WolframAlpha
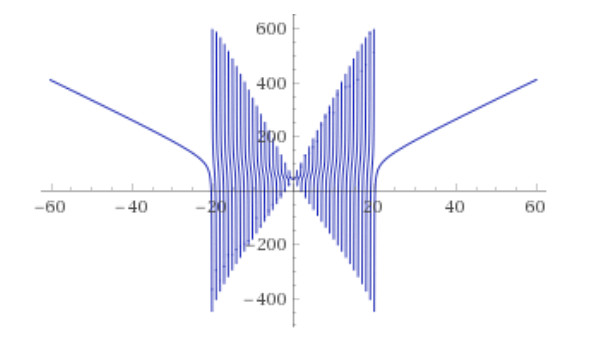
Plot[ Sum[abs(x)/(n-abs(x))+abs(x+n)/(n)+abs(x-n)/(n),{n,1,20}], {x,-60,60} ]
В данном выражении n лежит в диапазоне от 1 до 20, x лежит в диапазоне от -60 до 60.
Ссылка на рисунок.
«Задачник профильной направленности» М.И. Башмаков
«Элементарная математика» В.В.Зайцев, В.В.Рыжков, М.И.Сканави
«Математический анализ. Учебное пособие для IX — X классов» Виленкин Н.Я., Шварцбурд С.И.
Курс общей физики: в 3-х т. Т. 2. «Электричество и магнетизм» И.В. Савельев
Часть II
В данной статье рассматривается метод оценок диапазона принимаемых значений и связь этого метода с задачами, содержащими модуль.
При решении некоторых задач необходимо рассматривать диапазон, в пределах которого может находиться искомая величина.
Рассмотрим метод оценок при решении неравенств.
Дать оценку сверху означает определить максимальное значение, которое может принимать искомая величина.
Предположим, что цена за одну единицу товара может колебаться в пределах от 5 до 10 RUB. Для двух единиц товара оценка сверху составляет 10+10=20 RUB, оценка снизу 5+5=10 RUB.
Рассмотрим задачу из задачника профильной направленности М.И. Башмакова
37. Известны оценки для переменных
Дайте оценки сверху для следующих выражений:
1.
2.
5.
6.
8.
9.
Указание к решению задач
Для оценки этих значений необходимо воспользоваться следующим свойством числовых неравенств:
Если и оба числа положительны, то
и оба числа положительны, то 
Если и оба числа положительны, то
и оба числа положительны, то 
При умножении членов неравенства на одно и то же положительное число смысл неравенства не меняется, при умножении членов неравенства на одно и то же отрицательное число смысл неравенства меняется на противоположный.
Доказательство (Элементарная математика).
Пусть , тогда
, тогда  . Если
. Если  , то
, то  , так как произведение положительных чисел положительно. Раскрыв скобки в левой части последнего неравенства, получим
, так как произведение положительных чисел положительно. Раскрыв скобки в левой части последнего неравенства, получим  , т.е.
, т.е.  . Аналогичным образом рассматривается случай
. Аналогичным образом рассматривается случай  .
.
Точно такой же вывод можно сделать и относительно деления частей неравенства на какое-либо отличное от нуля число, так как деление на число равносильно умножению на число
равносильно умножению на число  , а числа
, а числа  и
и  имеют одинаковые знаки.
имеют одинаковые знаки.
Если
Если
При умножении членов неравенства на одно и то же положительное число смысл неравенства не меняется, при умножении членов неравенства на одно и то же отрицательное число смысл неравенства меняется на противоположный.
Доказательство (Элементарная математика).
Пусть
Точно такой же вывод можно сделать и относительно деления частей неравенства на какое-либо отличное от нуля число, так как деление на число
Вообще, анализ бесконечно малых величин использует критерий оценки. А модуль (как окрестность) присутствует в самом определении предела последовательности.
Последовательность {a} называется сходящейся к числу a, если для любого
найдётся такое число N (зависящее от
), что при
выполняется неравенство
Определение эпсилон-окресности на примере радиоактивонго распада приводится в учебнике «Математический анализ. Учебное пособие для IX — X классов»
Процесс радиоактивного распада. Часто встречаются последовательности, которые «устанавливаются» лишь приближенно—все члены этих последовательностей, начиная с некоторого номера, весьма мало отличаются от некоторого числа a.
Рассмотрим процесс радиоактивного распада. Предположим, что мы взяли кусок радиоактивного вещества весом в 1024 г, причем за одни сутки вес вещества уменьшается в результате распада вдвое. Будем взвешивать наш кусок на весах, чувствительность которых равна 10 г. Вес вещества (если измерения производятся каждые сутки) дает последовательность
Ясно, что по истечении 7 суток, когда вещества осталось 8 г, весы с чувствительностью 10 г не дадут нам возможности отличить истинное положение вещей (наличие 8 г вещества) от полного отсутствия данного вещества.
Возьмем более точные весы, имеющие чувствительность в 1 г. Эти весы покажут, что после 7 суток вещество еще осталось. Но после 11 суток (когда вещества остаетсяг) и с их помощью не удается выяснить, есть еще вещество или нет. А весы с чувствительностью в 0,1 г покажут отсутствие вещества лишь по истечении 14 суток (когда на самом деле его останется
г). И какой бы чувствительности весы мы ни взяли, наступит момент, начиная с которого мы не сможем выяснить с их помощью, осталось вещество или нет.
Итак, последовательность чисел (1) обладает следующим свойством: какое бы числомы ни взяли (то есть какой бы чувствительности весы мы ни взяли), найдется номер N, начиная с которого члены последовательности отличаются от нуля меньше, чем на
.
Определение бесконечеого ряда
Пусть задана некоторая бесконечная последовательность чисел:
…
Станем последовательно складывать члены ряда, составляя (в бесконечном количестве) суммы
Их называют частичными суммами ряда.
Конечный или бесконечный предел А частичной суммы при
называют суммой ряда…
Если в ряде отбросить первые m членов, то получится ряд:
называемый остатком ряда после m-ного члена
Если сходится ряд, то сходится и любой из его остатков; обратно, из сходимости остатка вытекает сходимость исходного ряда.
…
Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд — сходящимся), если частичные суммы ряда ограничены сверху, и бесконечной (а ряд — расходящимся) в противном случае.
Вернёмся к задаче
38. Вычислить сумму
Ряд
Отбросим первое слагаемое
Код
0.41666666666666663
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941
Проверить можно в ideone.com здесь
(define series_sum_1
( lambda (n)
(if (= n 0) 0
(+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0)))
) ) )
(writeln (series_sum_1 10))
(writeln (series_sum_1 100))
(writeln (series_sum_1 1000))
(writeln (series_sum_1 10000))
(writeln (series_sum_1 100000))
(writeln (series_sum_1 1000000))
0.41666666666666663
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941
Проверить можно в ideone.com здесь
Этот же алгоритм на Python
Ссылка на ideone.com
def series_sum(n):
if n==0:
return 0
else:
return 1.0/((n+1.0)*(n+2.0))+series_sum(n-1.0)
print(series_sum(10))
print(series_sum(100))
Ссылка на ideone.com
Получим
Отбросим первое и второе слагаемые и рассмотрим остаток ряда.
Код
(define series_sum_1
( lambda (n)
(if (= n 0) 0
(+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0)))
) ) )
(series_sum_1 1000000)
Получим 0.33333233333632745
Если ряд сходится, то сумма его остатка после m-го члена с возрастанием m стремится к нулю.
У нас сумма остатка с возрастанием m стремится к нулю.
Верхняя и нижняя оценка
Рассмотрим пример из «Курса дифференциального и интегрального исчисления» 363(6)
Легко установить расходимость рядаДля того, чтобы доказать, что
В самом деле, так как члены его убывают, то n-я частичная сумма
и растёт до бесконечности вместе с.
Произведя сложение всех неравенств данной системы, получим
Следовательно, данный ряд расходится.
Для гармонического ряда этот метод не проходит, потому что
Подсчитаем сумму гармонического ряда при увеличении n
Получим:
2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989
Воспользуемся частичными суммами для того, чтобы установить, что сумма гармонического ряда неограничена сверху и растёт до бесконечности
#lang racket
(define series_sum_1
( lambda (n)
(if (= n 0) 0
(+ (/ 1.0 n) (series_sum_1(- n 1.0)))
) ) )
(series_sum_1 10)
(series_sum_1 100)
(series_sum_1 1000)
(series_sum_1 10000)
(series_sum_1 100000)
(series_sum_1 1000000)
Получим:
2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989
Воспользуемся частичными суммами для того, чтобы установить, что сумма гармонического ряда неограничена сверху и растёт до бесконечности
Имеем очевидное неравенство:
Если, отбросив первые два члена, остальные члены гармонического ряда разбить на группы почленов в каждой
то каждая из этих сумм в отдельности будет больше.
… Мы видим, что частичные суммы не могут быть ограничены сверху: ряд имеет бесконечную сумму.
Подсчитаем частичные суммы, которые получаются при отбрасывании
Рекурсивный алгоритм
Получаем:
0.5833333333333334
0.6345238095238095
0.6628718503718504
Напишем программу, которая вычисляет сумму гармонического ряда от до
до  , где
, где  при
при 
Проверить можно в online ide по ссылке
Получаем:
0.5833333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267
Для диапазона![$ \left[ 1+2^{70};2^{71}\right] $](https://habrastorage.org/getpro/habr/formulas/e34/5b7/fd6/e345b7fd6646007b5ede17919bb2d7f2.svg) получаем 0,693147…
получаем 0,693147…
Проверить моджно в Wolfram Cloud здесь.
#lang racket
(* 1.0 (+ 1/3 1/4))
(* 1.0 (+ 1/5 1/6 1/7 1/8))
(* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16))
Получаем:
0.5833333333333334
0.6345238095238095
0.6628718503718504
Напишем программу, которая вычисляет сумму гармонического ряда от
#lang racket
(define (Hn n )
(define half_arg (/ n 2.0))
(define (series_sum n)
(if (= n half_arg ) 0
(+ (/ 1.0 n) (series_sum(- n 1)) )
)
)
(series_sum n) )
(Hn 4)
(Hn 8)
(Hn 16)
(Hn 32)
Проверить можно в online ide по ссылке
Получаем:
0.5833333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267
Для диапазона
Проверить моджно в Wolfram Cloud здесь.
Переполнение стека
Данный рекурсивный алгоритм вызывает быстрое переполнение стека.
В этой статье есть пример вычисления факториала с помощью итеративного алгоритма. Изменим этот итеративный алгоритм так, чтобы он вычислял частичную сумму Hn внутри определённых границ; назовём эти границы a и b
(define (Hn a b)
(define (iteration product counter)
(if (> counter b)
product
(iteration (+ product (/ 1.0 counter))
(+ counter 1))))
(iteration 0 a))
Нижней границей является число
Напишем функцию, вычисляющую степень двойки
(define (power_of_two k)
(define (iteration product counter)
(if (> counter k)
product
(iteration (* product 2)
(+ counter 1))))
(iteration 1 1))
Будем в качестве нижней границы подставлять (+ 1 (power_of_two k)), а в качестве верхней можно использовать функцию (* 2 (power_of_two k)) или эквивалентную ей функцию (power_of_two (+ 1 k))
Перепишем функцию Hn
(define (Hn k)
(define a (+ 1 (power_of_two k)) )
(define b (* 2 (power_of_two k)) )
(define (iteration product counter)
(if (> counter b)
product
(iteration (+ product (/ 1.0 counter))
(+ counter 1))))
(iteration 0 a ))
Теперь можно вычислять Hn при больших значениях
Напишем на языке Си программу, которая замеряет время, необходимое на вычисление Hn. Будем использовать функцию clock() из стандартной библиотеки <time.h>
Статья про измерение процессорного времени есть на Хабре здесь.
#include <math.h>
#include <stdio.h>
#include <time.h>
int main(int argc, char **argv)
{
double count;
// k от 1+2^30 до 2^31
for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++)
{
count=count+1.0/i;
}
printf("Hn = %.12f ", count);
double seconds = clock() / (double) CLOCKS_PER_SEC;
printf("Программа работала %f сек \n", seconds);
return 0;
}
Обычно online ide ограничивают время выполнения запускаемых программ пятью секундами, поэтому эту программу можно проверить лишь в некоторых online ide, например, в onlinegdb.com или repl.it
При k от 1+2^30 до 2^31 время работы составит ~5 сек.
При k от 1+2^31 до 2^32 время работы составит ~10 сек.
При k от 1+2^32 до 2^33 время работы составит ~20 сек.
При k от 1+2^33 до 2^34 время работы составит ~40 сек.
При k от 1+2^34 до 2^35 время работы составит больше одной минуты.
…
При k от 1+2^45 до 2^46 время работы составит больше 24 часов.
Предположим, что для k от 1+2^30 до 2^31 время выполнения алгоритма составляет ~2 сек.
Тогда для k=2^(30+n) время выполнения алгоритма составляет 2^n сек. (при
Данный алгоритм имеет экспотенциальную сложность.
Вернёмся к модулям.
В интегральном исчислении модуль используется в формуле
Читайте также Самый натуральный логарифм.
Присутствие модуля в формуле
Если…, то дифференцированием легко убедиться в том, что
Физическое приложение интеграла 
Этот интеграл используется для вычисления разности потенциалов обкладок цилиндрического конденсатора.
«Электричество и магнетизм»:
Разность потенциалов между обкладками находим путем интегрирования:Здесь не используется знак модуля под знаком натурального логарифма
(и
— радиусы внутренней и внешней обкладок).
«Модульное» рисование
С помощью модулей можно рисовать различные фигуры.
Если в программе geogebra написать формулу
Можно рисовать более сложные фигуры. Нарисуем, например, «бабочку» в облаке WolframAlpha
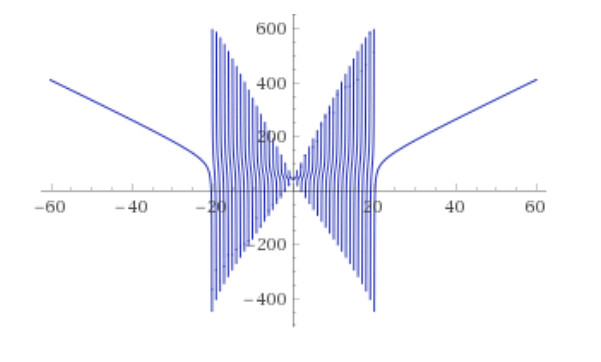
Plot[ Sum[abs(x)/(n-abs(x))+abs(x+n)/(n)+abs(x-n)/(n),{n,1,20}], {x,-60,60} ]
В данном выражении n лежит в диапазоне от 1 до 20, x лежит в диапазоне от -60 до 60.
Ссылка на рисунок.
Книги:
«Задачник профильной направленности» М.И. Башмаков
«Элементарная математика» В.В.Зайцев, В.В.Рыжков, М.И.Сканави
«Математический анализ. Учебное пособие для IX — X классов» Виленкин Н.Я., Шварцбурд С.И.
Курс общей физики: в 3-х т. Т. 2. «Электричество и магнетизм» И.В. Савельев






