Дано: 12 монет, одна из них фальшивая, отличается только весом. Неизвестно легче или тяжелее. Даны рычажные весы, которые показывают, что груз с одной из сторон тяжелее. За 3 взвешивания необходимо найти фальшивую монетку.
Из опыта советую не спешить, решать письменно. Головоломка «12 монет, 3 взвешивания» несколько раз возникала в моей жизни. Первый раз ее задал мне мой товарищ-олимпиадник, решил я ее после олимпиады и пришлось пару часиков поломать голову. И через несколько лет она далось мне не сразу. Если желаете решить самим — делайте на листочке.
Ниже будет разбор и этапы решения. Этапы проведут по универсальной методике решения задач, которая применима как к программированию, так и к жизни. Благодаря подходу решение головоломки станет простым.
Предлагаю вам, прежде чем читать предложить решение. У вас есть ответ? Проверенный?
Если бы это было программного обеспечения вопросы были бы следующие: «Вы запрограммировали, протестировали алгоритм? Рассмотрели тестовые случаи и проверили их?».
Как показывает опыт, чтобы решить требуется нарисовать дерево решений и проверить все 12 случаев.

Из опыта советую не спешить, решать письменно. Головоломка «12 монет, 3 взвешивания» несколько раз возникала в моей жизни. Первый раз ее задал мне мой товарищ-олимпиадник, решил я ее после олимпиады и пришлось пару часиков поломать голову. И через несколько лет она далось мне не сразу. Если желаете решить самим — делайте на листочке.
Ниже будет разбор и этапы решения. Этапы проведут по универсальной методике решения задач, которая применима как к программированию, так и к жизни. Благодаря подходу решение головоломки станет простым.
Предлагаю вам, прежде чем читать предложить решение. У вас есть ответ? Проверенный?
Если бы это было программного обеспечения вопросы были бы следующие: «Вы запрограммировали, протестировали алгоритм? Рассмотрели тестовые случаи и проверили их?».
Как показывает опыт, чтобы решить требуется нарисовать дерево решений и проверить все 12 случаев.

1. Подсказки
В процессе решения поможет:
1) Понижение энтропии (меры неопределенности) и ответы на вопросы:
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
1) Понижение энтропии (меры неопределенности) и ответы на вопросы:
- Что узнали на предыдущем шаге?
- Что снижает неопределённость?
- Какой информацией располагаем?
- Что еще нужно узнать?
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
2. Декомпозиция
Какие вопросы вы сформулировали для декомпозиции? Есть совпадения?
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
3. Решение
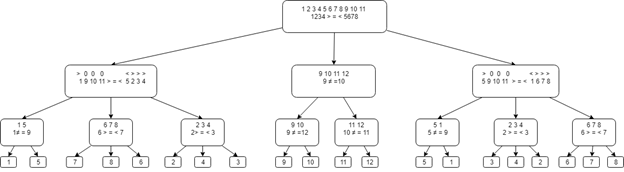
Первый шаг: разделим монеты на 3 группы по 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Сравним первые две группы. Возможны три варианта:

1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.
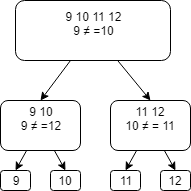
Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
Таким образом мы нашли фальшивую монету.
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».

Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
3) Случай когда вторая группа тяжелее первой, аналогичен второму.

Общая диаграмма «Дерева решений» представлена ниже.
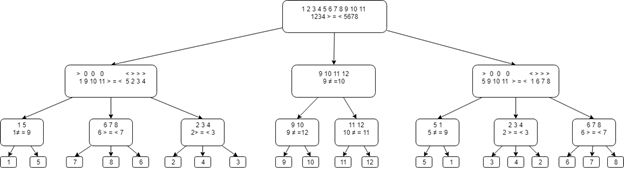
Сравним первые две группы. Возможны три варианта:
- первая группа тяжелее;
- вторая группа тяжелее;
- равны.

1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.
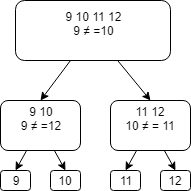
Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
- если они равны, то фальшивая монета во второй группе – сравниваем 9 и 11. Если 9 и 11 равны — то фальшивая – 12, если нет -11
- если они не равны, то фальшивая в первой группе – сравниваем 10 и 12. Если 10 и 12 равны – фальшивая – 9, если нет – 10.
Таким образом мы нашли фальшивую монету.
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».

Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
- Равны. Фальшивая монета находится среди чисел: 6 7 8. Сравниваем 6 и 7, если равны – фальшивая — 8, если 6 больше, то фальшивая – 7, если 7 больше, то фальшивая – 6, так как в данном случае фальшивая монета легче.
- Первая группа тяжелее, то фальшивая монета либо 1, либо 5. Сравниваем 1 и 9, если они равны – фальшивая монета — 5, если нет — 1.
- Первая группа легче, то фальшивая среди монет 2 3 4, так как известно, что 9, 10 и 11 настоящие, и перевесить вторая группа может только за счет монет 2, 3 и 4. Сравниваем 2 и 3, если равны – фальшивая 4, если 2 тяжелее, то фальшивая – 2, иначе 3-я является фальшивой.
3) Случай когда вторая группа тяжелее первой, аналогичен второму.
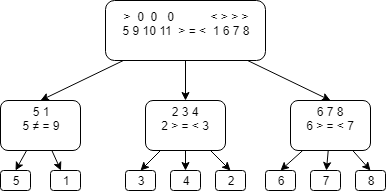
Общая диаграмма «Дерева решений» представлена ниже.
Заключение
При поступлении задачи на доработку или отладку хорошо применить рассмотренный выше подход:
Успешных решений.
- Определиться, что дано?
- На какие элементарные случаи\задачи можно разложить?
- Что неизвестно для решения задачи? Какие эксперименты нужно провести, чтобы снизить энтропию?
- Выполнить.
- Задача решена? Нет? Вернуться к шагу 1.
Успешных решений.






