Предисловие

В лето 2016 от всем известного события вашему покорному слуге в числе группы других студентов удалось побывать на лекциях профессора Мартина Хаардта по тематике MIMO, проводимых им в рамках международной магистерской программы "Communication and Signal Processing". Но, к сожалению, полторы недели из двух я довольно сильно проболел — и поэтому тогда ряд тем просто выпал у меня из сферы достаточного понимания… Однако, уже по прошествии некоторого времени разбор основ MIMO стал моим хобби — не оставлять же дело незаконченным.

По-немногу всё это выросло в ряд небольших конспектов-семинаров, не поделиться которыми, наверное, было бы неправильным. И вот сегодня, в честь Дня связи, мне бы хотелось разобрать с вами тему пропускной способности MIMO канала — тему несложную, но всё же вызывающую определенные трудности у студентов (и не только у студентов).

Людям непричастным может казаться, что увеличение количества приёмных и предающих антенн в рамках названной технологии ровно на столько же увеличивает и пропускную способность системы: например, если поставить 2 антенны на приёмной стороне и 2 антенны на передающей (MIMO 2x2), то пропускная способность однозначно увеличится в 2 раза. Но так ли это хотя бы в теории? Попробуем разобраться!

Более формальную версию на английском языке можно найти по ссылке и в моём GitHub репозитории.
В рамках данной статьи мы не будем рассматривать вопросы корреляции антенн и прочие вопросы реализации. Ограничимся дистиллированной теорией — для начала.

Модель принятого сигнала

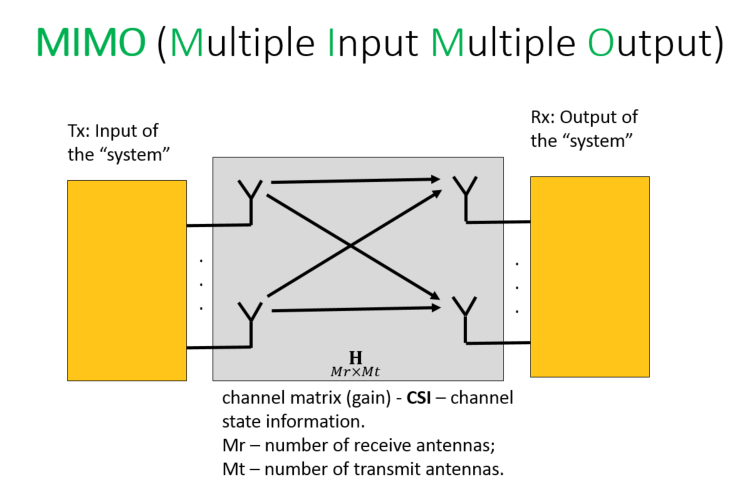
Прежде чем мы начнем говорить о пропускной способности, разберемся сначала с математическим описание полученного сигнала (received signal). К этой части стоит отнестись достаточно внимательно, так как очень многое будет проистекать именно из этой формулы. Итак принятый сигнал можно представить как:

$\mathbf{y} = \sqrt{\frac{P}{M_T}}\mathbf{H}\mathbf{s} + \mathbf{n} \qquad (1)$

где — мощность передатчика, M_T — количество передающих антенн, $\mathbf{s}$ — передаваемые символы, $\mathbf{n}$ — аддитивный шум, а $\mathbf {H}$ — матрица коэффициентов передачи канала (фактически, процесс затухания — fading).

Переданный сигнал тоже можно расписать чуть более подробно:

$s_i = \gamma_i d_i \quad i=1,2,..M_T \qquad (2)$

где — один из информационных сигналов ( $E \{\mathbf{d}\mathbf{d}^H\} = M_T$ ), а $\gamma_i$ — усиление определенного пути распространения ЭМ волны (path gain).

Сформулируем, что такое усиление пути:
Усиление пути распространения (или вес антенны — antenna weight) означает распределение выходной мощности, пропорциональное "силе" определенной трассы. Другими словами, мы хотим выделить больше мощности для хороших каналов (путей распространения) и меньше энергии для плохих каналов.

Веса антенн ограничены количеством передающих антенн:

$\sum^r_{i=1} \gamma_i = M_T \qquad(3)$

где — ранг канальной матрицы.

Кстати, о последней.

Размерность матрицы $\mathbf{H}$ составляет $M_R \times M_T$ , где M_R — количество приемных антенн.
Для нескольких временных замеров канал будет иметь следующий вид:

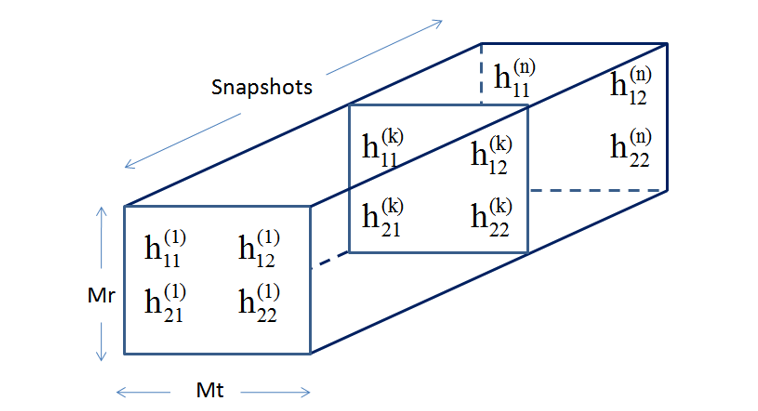
Для справки:
Возможно, для более сложных расчетов и моделей вы захотите использовать один из самых популярных для того инструментов — MatLab. В таком случае, стоит учесть, что там используется немного другая структура данных: строками являются временные замеры (snapshots), количество столбцов соответствует количеству передающих антенн , измерению "вглубь" (lateral dimension) соответствует .

Формула (1) легко может быть адаптирована и под частные случаи MIMO.

MISO (Multiple Input Single Output — несколько передающих антенн и одна приемная):

$y = \sqrt{\frac{P}{M_T}}\mathbf{h}\mathbf{s} + n \qquad (4)$

где $\mathbf{h}$ — это вектор $1\times M_T$ .

SIMO (Single Input Multiple Output — несколько приемных антенн и одна передающая):

$y = \sqrt{P}\mathbf{h}s + \mathbf{n} \qquad (5)$

где $\mathbf{h}$ — это вектор $M_R \times 1$

SISO (Single Input Single Output — по одной антенне на приемной и передающей сторонах):

$y = \sqrt{P}hs + n \qquad (6)$

Вроде бы, пока несложно.

Всё дальнейшее рассмотрение можно поделить на два больших кейса: информация о состоянии канала (CSI — channel state information) неизвестна передатчику (CU — Channel Unknown) и информация о состоянии канала известна передатчику (CK — Channel Known).

Выше мы рассмотрели случай, когда канал неизвестен для передатчика (open-loop case, передача без обратной связи). Другими словами, мы не можем, в силу отсутствия необходимой информации, выбрать какое-либо эффективное направление, и поэтому идем по самому простому пути: передаем равную мощность через все антенны (тракты, пути распространения). Следовательно, усиление каждого пути распространения (path gain) равно 1:

$\gamma_i=1, \quad i=1,2,.. M_T \qquad (7)$

Однако повторим: мы хотим выделить больше мощности для хороших каналов (путей распространения) и меньше энергии для плохих каналов.

Возникает вопрос: как эффективно распределить мощность?

Если канал известен (closed-loop case — с обратной связью), мы можем использовать расширенные сценарии передачи с некоторыми дополнительными алгоритмами обработки сигналов. Например, с линейными подходами такими, как предварительное кодирование (pre-coding) и пост-обработка (post-processing).

Разберемся, что означают два последних термина.

Если у нас есть CSI на передающей стороне, т.е. матрица $\mathbf{H}$ , эту самую матрицу мы можем математически обработать. Например, применив алгоритм SVD (Singular Value Decomposition).

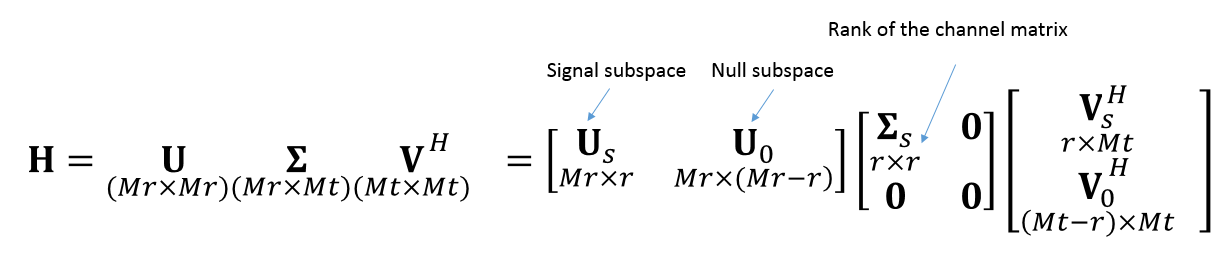
Обратите внимание, что матрица $\mathbf{\Sigma}$ — диагональная матрица, а элементы её диагонали (сингулярные значения) — это, по сути своей, коэффициенты передачи уникальных путей распространения. Иначе говоря, если мы добьемся перемножения нашего сигнала на матрицу сингулярных значений $\mathbf{\Sigma}$ , а не на полную канальную $\mathbf{H}$ , то канал MIMO распадется на массив параллельных SISO каналов.

Значит матрица линейного предварительного кодирования (фильтра) должна быть $\mathbf{F} = \mathbf{V}_s$ , а матрица линейной пост-обработки (демодулятор) $\mathbf{D} = \mathbf{U}^H_s$ (H обозначает эрмитово сопряжение).

Очевидно, что для случая с неизвестным каналом $\mathbf{F}$ и $\mathbf{D}$ равны единичным (identity) матрицам.

Теперь, зная всё выше отмеченное, давайте переопределим модель принятого сигнала:

$\mathbf{Dy} = \mathbf{D}\left( \sqrt{\frac{P}{M_t}}\mathbf{H}\mathbf{F}\mathbf{s} + \mathbf{n} \right) = \mathbf{U}^H_s\mathbf{y} = \sqrt{\frac{P}{M_t}}\mathbf{U}^H_s\mathbf{H}\mathbf{V}_s\mathbf{s}+\mathbf{U}^H_s\mathbf{n} = \sqrt{\frac{P}{M_t}}\mathbf{\Sigma}_s\mathbf{s} + \mathbf{\hat{n}} = \mathbf{\hat{y}}\qquad (8)$

Отметим, что:

$\mathbf{\hat{n}}$ имеет те же статистические свойства, что и $\mathbf{n}$ ;
Собственные значения (eigen values) $\mathbf{HH}^H$ являются квадратами сингулярных значений (singular values) матрицы канала $\mathbf{H}$ ( $\sigma_i = \sqrt{\lambda_i}$ ).

Схематически это можно представить как:

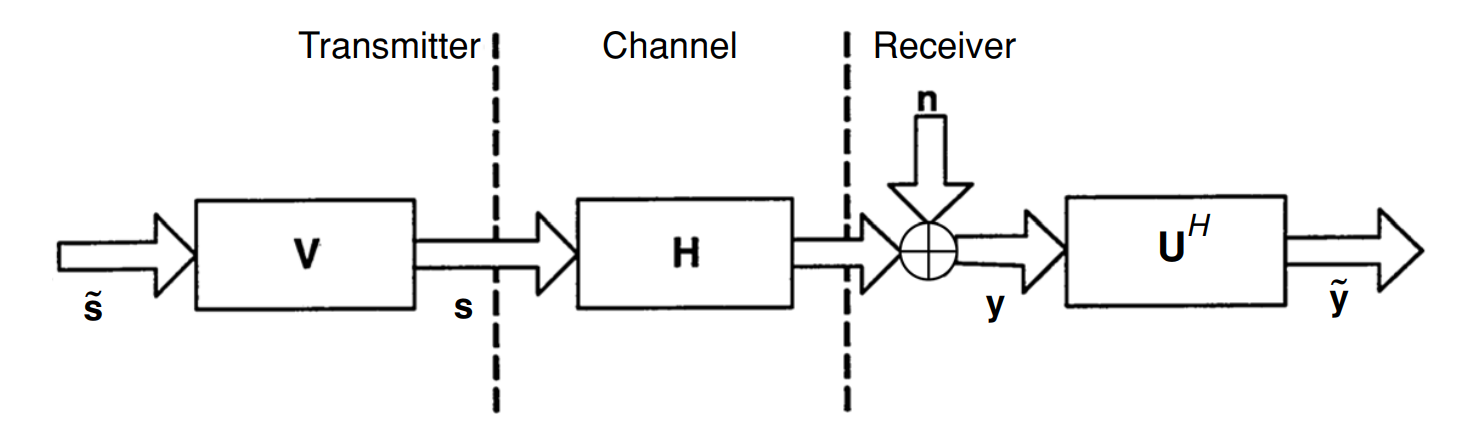
Рис. 1. Схема пре-кодирования и пост-обработки [1, с.67 ].

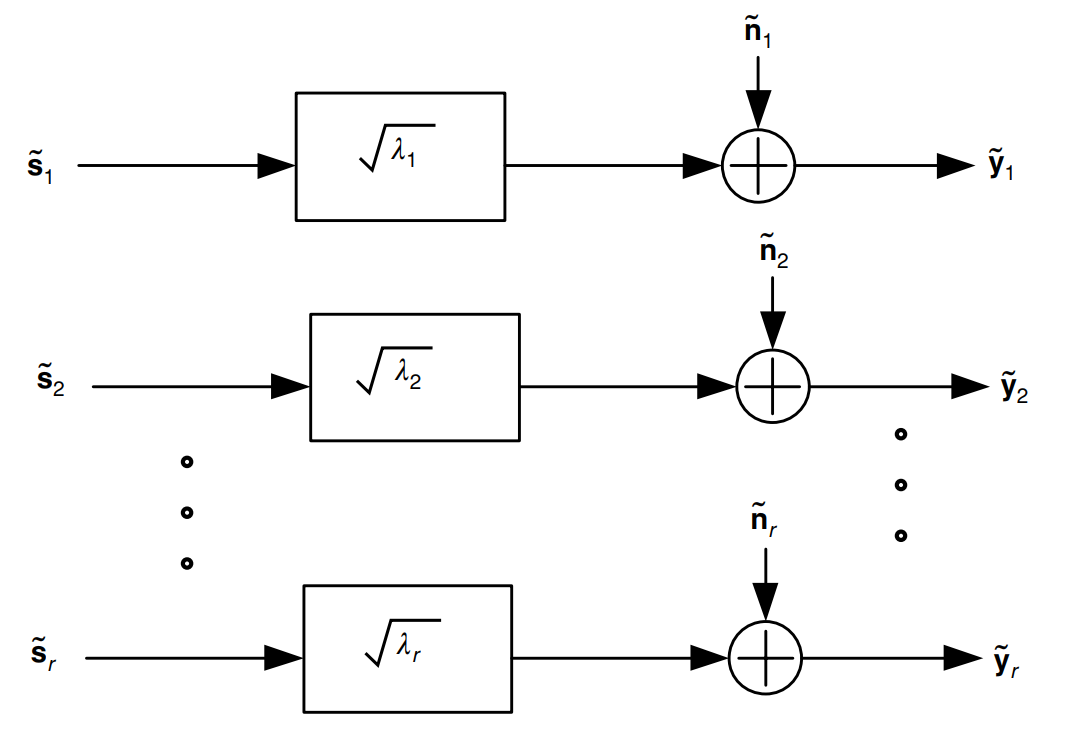
Рис. 2. Схема модального разложения $\mathbf{H}$ , когда канал известен передатчику и приёмнику [1, с.67 ].

Азы разобраны — можем приступать непосредственно к пропускной способности!

Пропускная способность (capacity)

Я думаю, все, кто изучал теорию информации, помнят, что термин пропускной способности пришёл к нам именно из этой дисциплины. Обычно (на моём студенческом веку) рассмотрение останавливалось на классическом случае AWGN канала, однако формулу относительно легко можно вывести и для случая MIMO канала с замираниями.

Чтобы не перепечатывать в очередной раз выкладки из книжек, я постарался оформить всё более или менее красочно и от руки — дабы придать формулам жизни, так сказать. Надеюсь, такой формат будет менее утомительным.

Итак, ещё раз запишем модель сигнала:

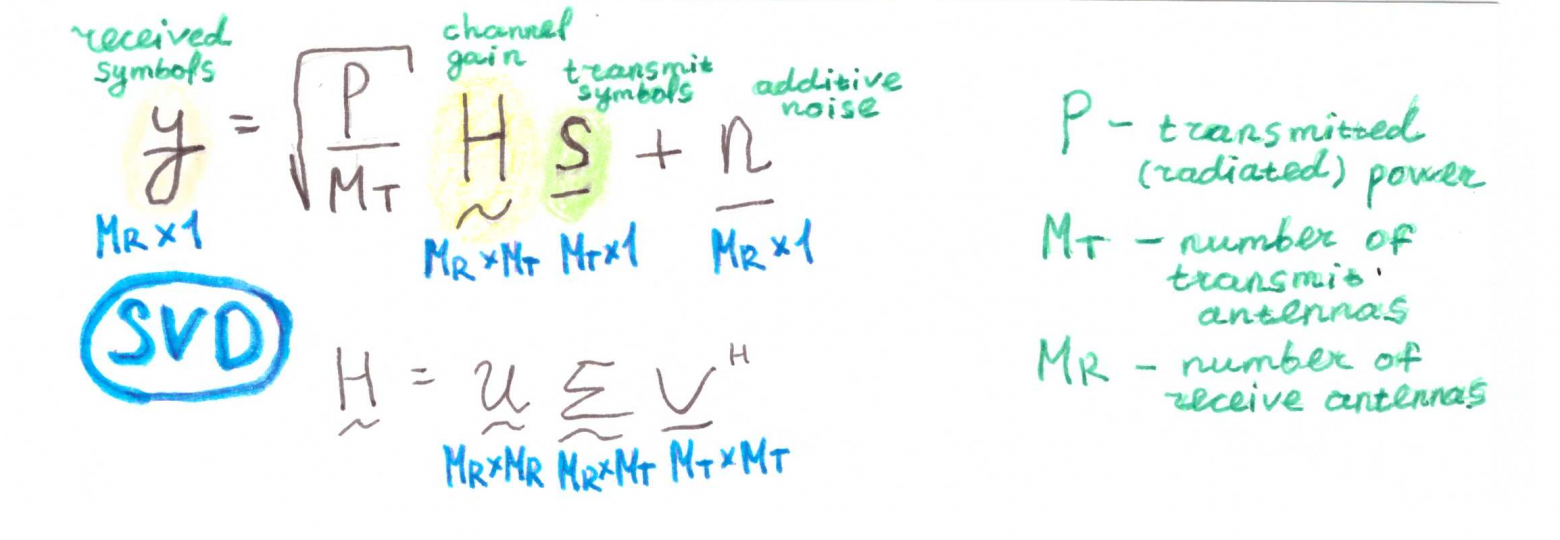
Теперь перейдем к определению пропускной способности через взаимную информацию.

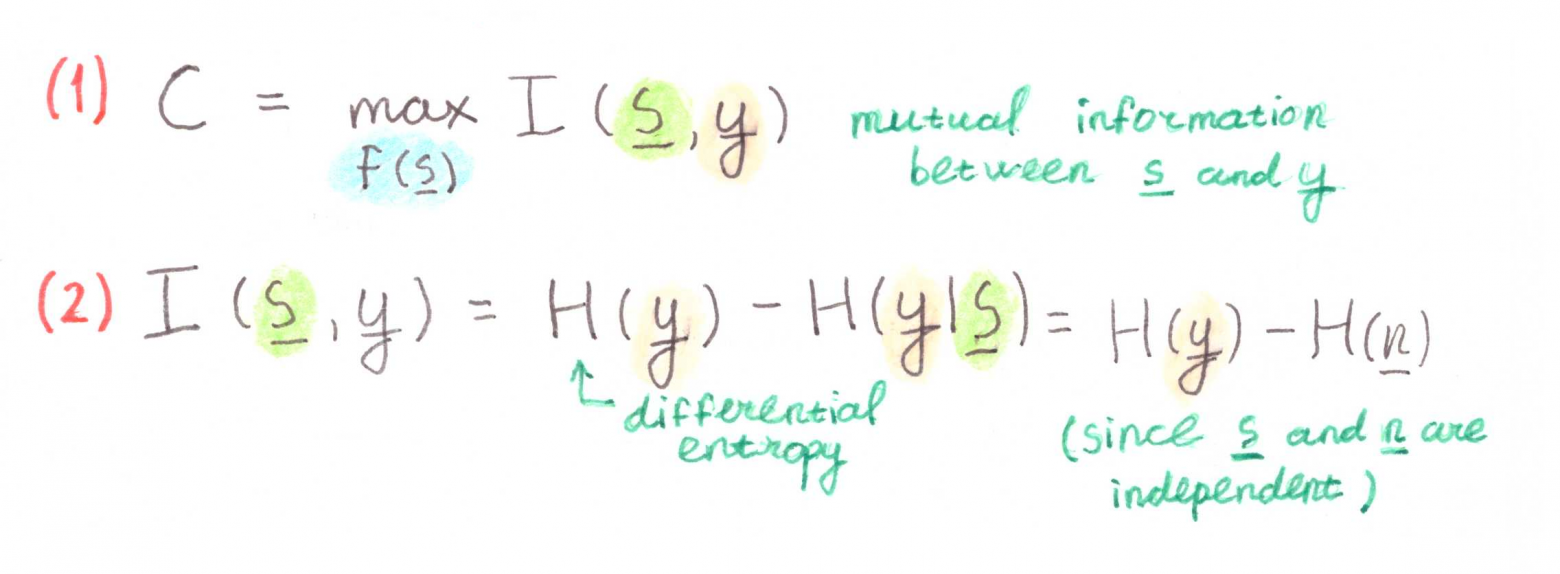
Запишем автоковариационную матрицу принятого сигнала и её составляющие:

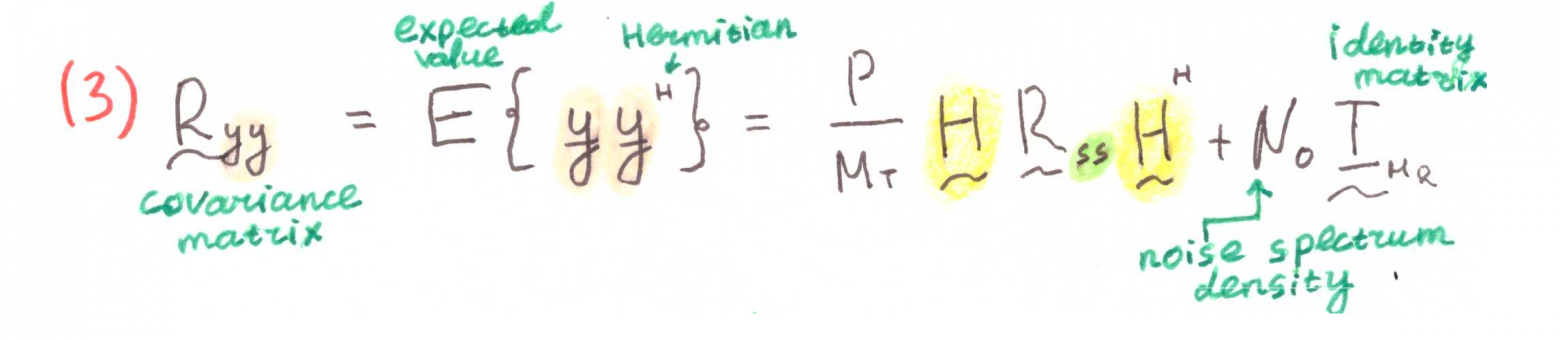
И используем их при определении дифференциальной энтропии:

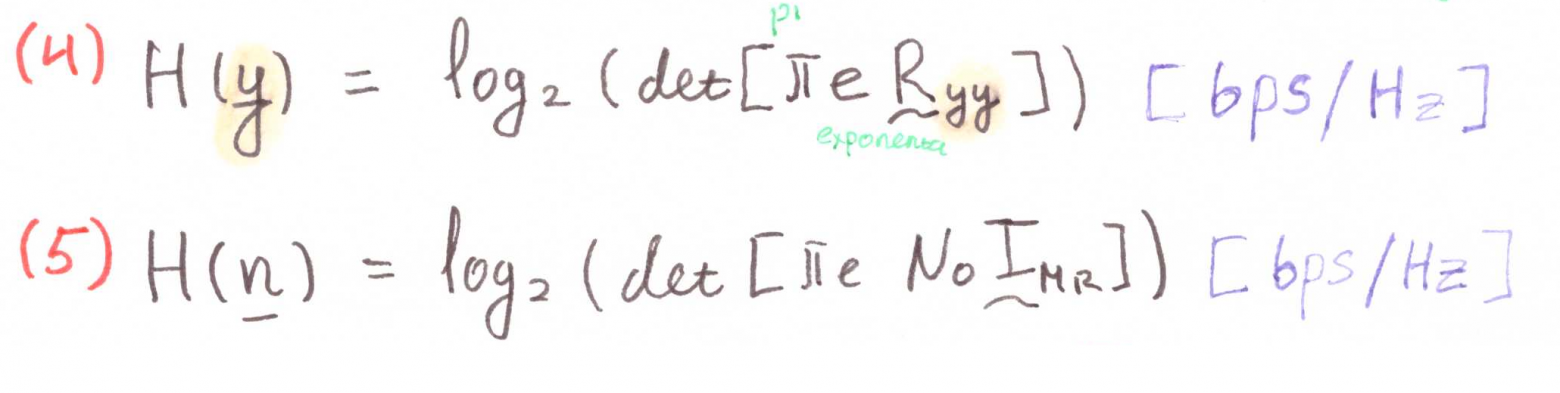
Подставляем (4) и (5) в (2):

А теперь подставляем (6) в (1) :

Продолжаем рассуждать. Возьмем первый случай: канал неизвестен (Channel Unknown). Это значит для нас, что выбрать оптимальное направление передачи невозможно, и, следовательно, передаваемые сигналы будут независимыми и будут иметь одинаковую мощность (equi-powered). Исходя из условия максимума ( $Tr\{\mathbf{R}_{ss}\} = M_T$ ), можно принять автоковариационную матрицу переданных символов равной единичной матрице (identity). Тогда имеем:

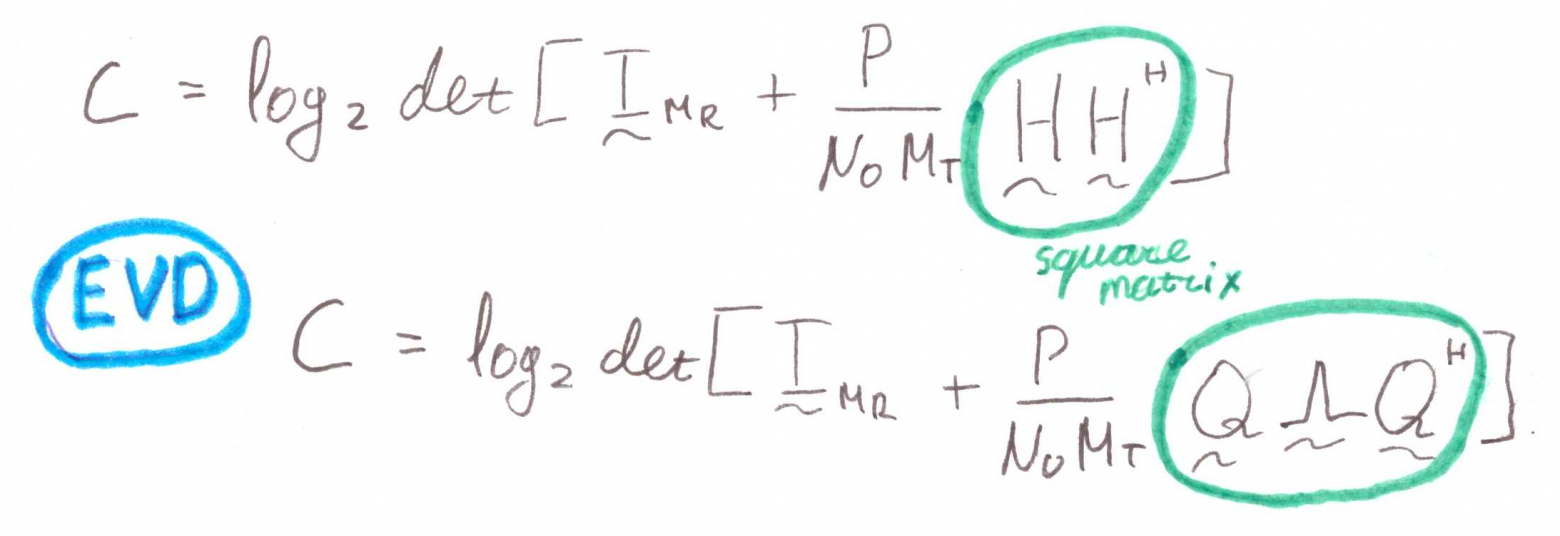
Воспользуемся следующим свойством определителей:

$det\left(\mathbf{I}_m + \mathbf{AB} \right) = det\left(\mathbf{I}_n + \mathbf{BA} \right)$

Это наш случай, и можно поменять местами матрицы так, что бы $\mathbf{Q}\mathbf{Q}^H = \mathbf{I}$ (из свойств EVD). Останется:

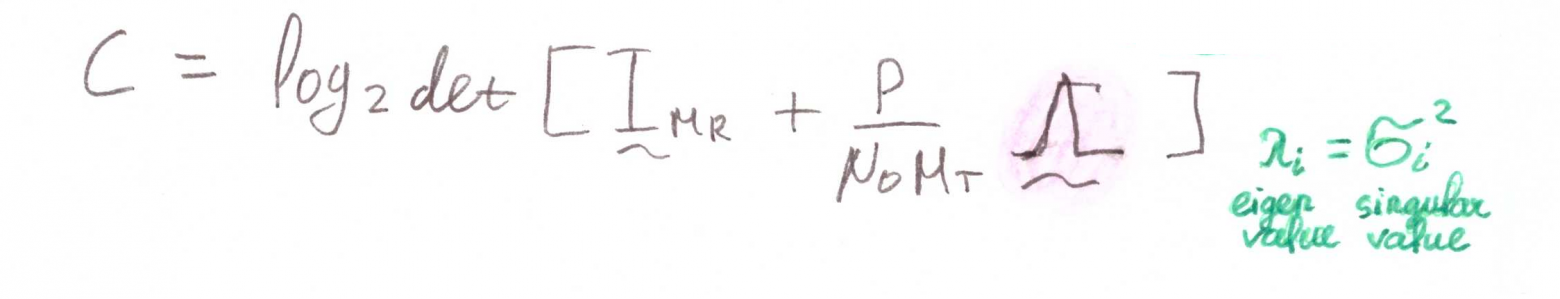
Переходя от матриц к суммам, имеем:

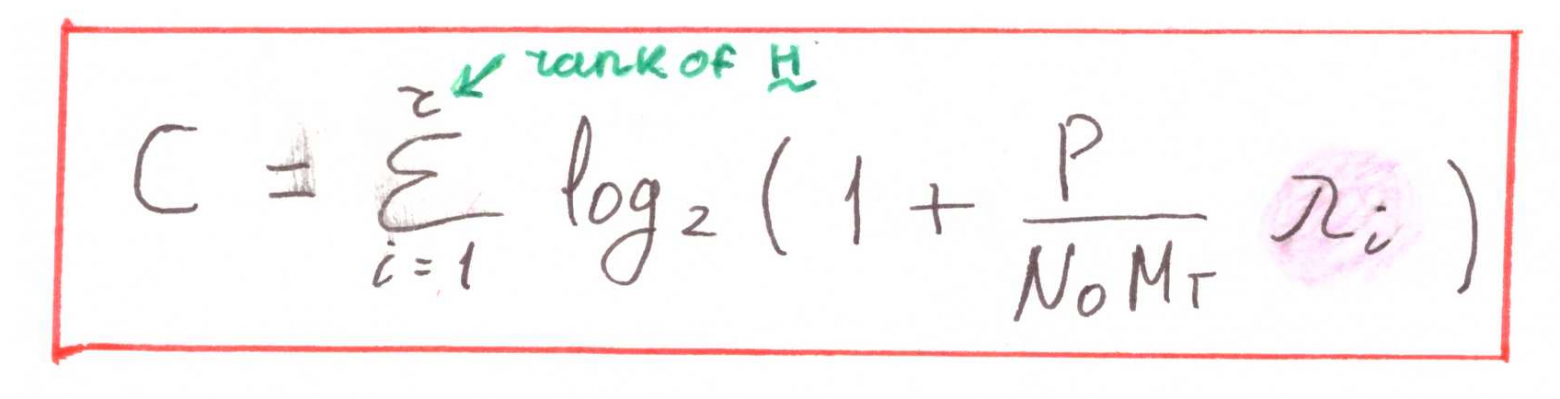
Эта формула ещё раз иллюстрирует подход рассмотрения MIMO как параллельные SISO каналы.
Для случая с известным каналом (Channel Known) в формулу добавятся веса антенн:

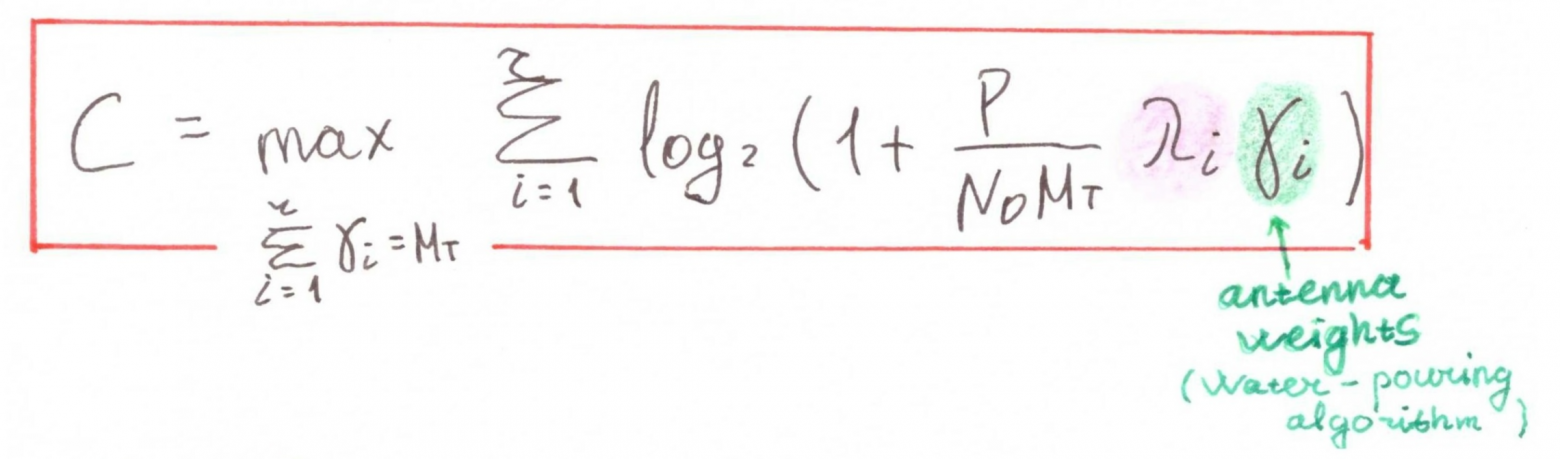
Запишем также формулы для частных случаев:

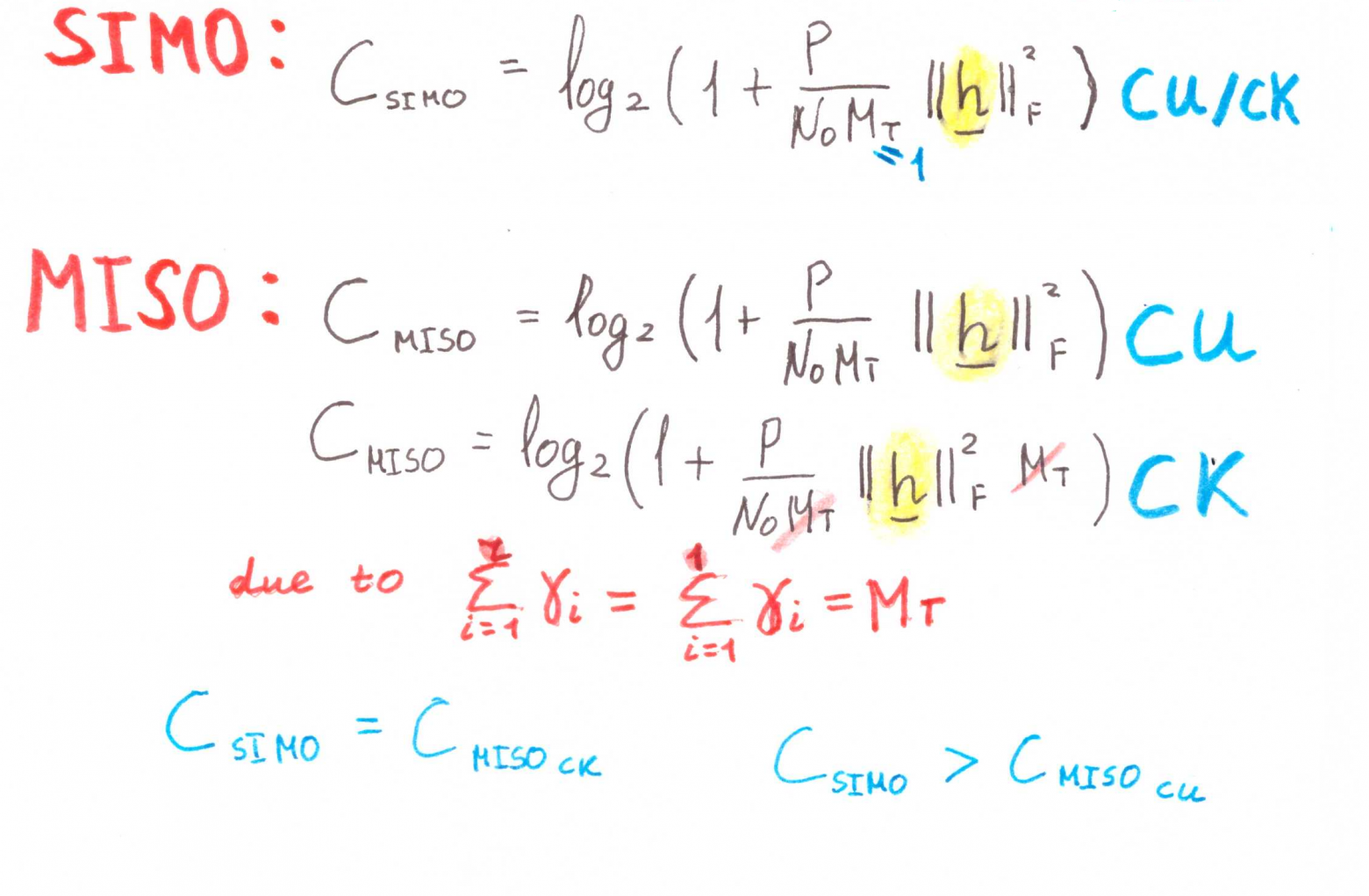
Отметим:
Для случаев SIMO и MISO не зря в записи фигурируют квадраты нормы Фробениуса $||\mathbf{h}||_F^2$ — с математической точки зрения они эквивалентны собственным числам $\mathbf{h}\mathbf{h}^H$ . Поэтому, если нужно что-то быстро посчитать от руки — вот он способ.

Ну, надеюсь, мой почерк и мой английский не сильно помешали восприятию информации, однако всё же давайте, проговорим основную мысль:

Да, пропускная способность канала MIMO может рассматриваться как сумма пропускной способности каналов SISO.
Однако, сумма эта ограничена рангом канала!

Алгоритм Water-pouring

Как видно из формулы пропускной способности известного на передающей стороне канала (CK — Channel Known), распределение энергии по антеннам можно оптимизировать. Для этого воспользуемся алгоритмом Water-pouring (заполнение водой) [1, с.68-69]:

import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt

def waterpouring(Mt, SNR_dB, H_chan):
    SNR = 10**(SNR_dB/10)
    r = LA.matrix_rank(H_chan)
    H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H)
    lambdas = LA.eigvals(H_sq) 
    lambdas = np.sort(lambdas)[::-1]
    p = 1;
    gammas = np.zeros((r,1))
    flag = True
    while flag == True:
        lambdas_r_p_1 = lambdas[0:(r-p+1)]
        inv_lambdas_sum =  np.sum(1/lambdas_r_p_1)
        mu = ( Mt / (r - p + 1) ) * ( 1 + (1/SNR) * inv_lambdas_sum)
        for idx, item in enumerate(lambdas_r_p_1):
            gammas[idx] = mu - (Mt/(SNR*item))
        if gammas[r-p] < 0: #due to Python starts from 0
            gammas[r-p] = 0 #due to Python starts from 0
            p = p + 1
        else:
            flag = False
    res = []
    for gamma in gammas:
        res.append(float(gamma))
    return np.array(res)

Тестируем:

Mt = 3
SNR_db = 10
H_chan = np.array([[1,0,2],[0,1,0], [0,1,0]], dtype = float)
gammas = waterpouring(Mt, SNR_db, H_chan)
print('Rank of the matrix: '+str(LA.matrix_rank(H_chan)))
print('Gammas:\n'+str(gammas))

>>> Rank of the matrix: 2
>>> Gammas:
>>> [1.545 1.455]

Что ж, выглядит разумно:
1) количество задействованных передающих антенн равно рангу канала;
2) сумма весов антенн равна количеству передающих антенн.

Два предельных случая

А теперь давайте немного отвлечемся и порешаем задачки на понимание.

Найдём, к примеру, чему будут равны коэффициенты $\gamma_i$ при SNR стремящемся к $+\infty$ и $-\infty$ (в логарифмическом, конечно же, масштабе, ибо отрицательных мощностей не бывает).

Вспоминаем формулу соответствия между децибелами и разами:

$SNR_{dB} = 10log_{10}\left( \frac{S}{N} \right)$

где — мощность передаваемого сигнала (для наших задач она эквивалентна энергии символа E_s ), а — мощность шума (в нашей задаче равна спектральной плотности шума N_0 ).

Значит в линейном масштабе будет:

$\frac{E_s}{N_0} \equiv \frac{S}{N} = 10^{SNR_{dB}/10}$

Смотрим на основные формулы алгоритма:

$\mu = \frac{M_T}{(r-p+1)}\left[ 1 + \frac{N_0}{E_s} \sum_{i=1}^{r-p+1} \frac{1}{\lambda_i}\right]$

где — это итератор, начинающийся с 1, — ранг канальной матрицы, $\lambda_i$ — i-ое собственное значение "квадрата" канальной матрицы. Гаммы считаем по следующей формуле:

$\gamma_i = \left( \mu - \frac{M_TN_0}{E_s\lambda_i} \right) \quad i=1,2,...,r-p+1$

Начинаем рассуждать:

Если $SNR_{dB} \to +\infty$ , то и $\frac{E_s}{N_0} \to +\infty$ . Следовательно, $\frac{N_0}{E_s} \to 0$ . Для первой итерации остаётся:

$\mu = \frac{M_T}{r}$

Подставляем к гаммам:

$\gamma_i = \mu = \frac{M_T}{r} \quad i=1,2,...,r$

Резюмируем:

При бесконечно большой энергии передачи или бесконечно малых шумах ничего особого выдумывать, скажем так, не нужно — равномерно распределяем мощность между передающими антеннами (с оглядкой на ранг канальной матрицы).

Рассуждаем дальше:

А чему соответствует случай SNR стремящийся к $-\infty$ ? Здесь даже не будем лезть в математику, рассудим логически: случай этот соответствует либо бесконечно большим шумам, либо нулевой мощности передачи. Значит, так и так, система наша, считайте, не функционирует. Поэтому и вопрос с гаммами отпадает автоматически...

Вот такие иногда вопросы попадаются на экзамене у профессора.

Считаем пропускную способность (наконец-то!)

def siso_capacity(H_chan, SNR_dB):
    SNR = 10**(SNR_dB/10)
    c = np.log2(1 + SNR*(np.abs(H_chan)**2))
    return c

def openloop_capacity(H_chan, SNR_dB):
    SNR = 10**(SNR_dB/10)
    Mt = np.shape(H_chan)[1]
    H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H)
    lambdas = LA.eigvals(H_sq) 
    lambdas = np.sort(lambdas)[::-1]
    c = 0
    for eig in lambdas:
        c = c + np.log2(1 + SNR*eig/Mt)
    return np.real(c)

def closedloop_capacity(H_chan, SNR_dB):
    SNR = 10**(SNR_dB/10)
    Mt = np.shape(H_chan)[1]
    H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H)
    lambdas = LA.eigvals(H_sq) 
    lambdas = np.real(np.sort(lambdas))[::-1]
    c = 0
    gammas = waterpouring(Mt, SNR_dB, H_chan)
    for idx, item in enumerate(lambdas):
        c = c + np.log2(1 + SNR*item*gammas[idx]/Mt)
    return np.real(c)

Mr = 4
Mt = 4
H_chan = (np.random.randn(Mr,Mt) \
          + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) #Rayleigh flat fading

c = openloop_capacity(H_chan, 10)
print(c)
c = closedloop_capacity(H_chan, 10)
print(c)
c = siso_capacity(H_chan[0,0], 10)
print(c)  

>>>  11.978909197556913
>>>  12.342571770086721
>>>  3.9058582578551193

Кажется, работает. Переходим к более предметным оценкам.

Ergodic capacity

Как видно из примеров выше, работаем мы со случайными процессами. И, честно говоря, ошибочно делать какие-либо выводы о случайных процессах по одной реализации. Даже при условии постоянного в статистическом смысле канала нужно некоторое усреднение по достаточно большому множеству.

Здесь нам и пригодится понятие эргодической пропускной способности (ergodic capacity):

$\hat{C} = E\left\{ C \right\} \qquad (9)$

где $E\{*\}$ обозначает мат. ожидание (expected value).

Моделируем.

Mr = 4
Mt = 4
counter = 1000
SNR_dBs = [i for i in range(1, 21)]
C_MIMO_CU = np.empty((len(SNR_dBs), counter))
C_MIMO_CK = np.empty((len(SNR_dBs), counter))
C_SISO = np.empty((len(SNR_dBs), counter))
C_SIMO = np.empty((len(SNR_dBs), counter))
C_MISO_CU = np.empty((len(SNR_dBs), counter))
C_MISO_CK = np.empty((len(SNR_dBs), counter))

for c in range(counter):
    H_MIMO = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2)
    H_SISO = H_MIMO[0,0]
    H_SIMO = H_MIMO[:,0].reshape(Mr,1)
    H_MISO = H_MIMO[0,:].reshape(1,Mt)
    for idx, SNR_dB in enumerate(SNR_dBs):
        C_MIMO_CU[idx, c] = openloop_capacity(H_MIMO, SNR_dB)
        C_MIMO_CK[idx, c] = closedloop_capacity(H_MIMO, SNR_dB)

        C_SISO[idx, c] = siso_capacity(H_SISO, SNR_dB)
        C_SIMO[idx, c] = openloop_capacity(H_SIMO, SNR_dB)

        C_MISO_CU[idx, c] = openloop_capacity(H_MISO, SNR_dB)
        C_MISO_CK[idx, c] = closedloop_capacity(H_MISO, SNR_dB)

C_MIMO_CU_erg = np.mean(C_MIMO_CU, axis=1)
C_MIMO_CK_erg = np.mean(C_MIMO_CK, axis=1)

C_SISO_erg = np.mean(C_SISO, axis=1)
C_SIMO_erg = np.mean(C_SIMO, axis=1)

C_MISO_CU_erg = np.mean(C_MISO_CU, axis=1)
C_MISO_CK_erg = np.mean(C_MISO_CK, axis=1)

plt.figure(figsize=(7, 5), dpi=600)

plt.plot(SNR_dBs, C_MIMO_CU_erg,'g-o', label='$M_R=4$, $M_T=4$ (CU)')
plt.plot(SNR_dBs, C_MIMO_CK_erg,'g-v', label='$M_R=4$, $M_T=4$ (CK)')

plt.plot(SNR_dBs, C_MISO_CU_erg, 'm-o', label='$M_R=1$, $M_T=4$ (CU)')
plt.plot(SNR_dBs, C_MISO_CK_erg, 'm-v', label='$M_R=1$, $M_T=4$ (CK)')

plt.plot(SNR_dBs, C_SISO_erg, 'k-', label='$M_R=1$, $M_T=1$')
plt.plot(SNR_dBs, C_SIMO_erg, 'c-', label='$M_R=4$, $M_T=1$')

plt.title("Ergodic Capacity")
plt.xlabel('SNR (dB)')
plt.ylabel('Capacity (bps/Hz)')
plt.legend()
plt.minorticks_on()
plt.grid(which='major')
plt.grid(which='minor', linestyle=':')
plt.show()

Рис.3. Кривые пропускной способности для разных схем передачи. Сравните с [1, c. 74].

Итак, мы видим, что

случай MIMO ожидаемо превосходит остальные, а с увеличением SNR необходимость в знании канальной матрицы уменьшается (см. пример с бесконечностями).
SIMO превосходит MISO при условии незнания передатчиком канала (мощность в MISO разделяется по всем антеннам, а не оптимально) и совпадает с MISO в случае известного канала.
SISO ожидаемо плетется в хвосте.

И царит над всем его величество ранг канальной матрицы, не позволяющий однозначно сопоставлять увеличение количества антенн с увеличением скорости передачи.

Такие дела.

Литература

(книжка хоть и одна, но какая!)

Paulraj, Arogyaswami, Rohit Nabar, and Dhananjay Gore.
Introduction to space-time wireless communications. Cambridge university press, 2003.

Оцениваем пропускную способность MIMO канала (алгоритм Water-pouring прилагается)