
Введение
Настоящая статья описывает результаты эксперимента проведенного в рамках проекта “Абсолютный курс валют”. Протокол эксперимента можно увидеть перейдя по ссылке.
Проект “Абсолютный курс валют” занимается анализом парных валютных курсов, выделением из них абсолютных валютных курсов и их анализом. В рамках проекта получена методика преобразования от парных курсов к абсолютным валютным курсам. Для этого определена абсолютная валюта ABS. Курсы всех имеющихся валют выражаются в отношении к ABS.
Детальное описание технологии приводится в статье “От валютных пар к абсолютным курсам валют”.
На сегодняшний день уже вышли несколько статей по применению метода абсолютных валютных курсов. Привожу две последние.
В статье “Исследование связанности мировых валют через корреляцию абсолютных курсов” описывается одно из применений технологии абсолютных валютных курсов. Дается формальный метод вычисления связи между различными валютами.
В статье “Портфельный метод Марковица применительно к валютному рынку” дается описывается недоступная ранее технология оптимизации валютного портфеля.
В далее описывается методика преобразования от парных (относительных) валютных курсов к абсолютным. Приводятся числовые параметры преобразования и методика их вычисления.
В файле-источнике ежедневно в автоматическом режиме подгружаются парные валютные курсы и из них вычисляются абсолютные.
Матрица преобразования была получена в 2017 году. Вычислялась она на реальных парных валютных курсах путем минимизации ошибки отклонения восстановленных парных курсов из абсолютных. С тех пор не проводился анализ ошибки на современных данных.
Описанные ниже неожиданные результаты проверки заставили разработать новую методику получения матрицы преобразования. Кроме того была обнаружена ошибка обработки импортируемых котировок.
Теоретические основания
Для получения абсолютных валютных курсов необходимо проделать следующее преобразование. Для начала парные курсы логарифмируем. Далее умножаем их на матрицу обратного преобразования. В конце обратно возвращаем из логарифмической шкалы применением экспоненты.
Для дальнейшего перехода к парным курсам необходимо абсолютные курсы прологарифмировать. Затем умножить на матрицу прямого преобразования. Завершаем как и ранее применением экспоненты.
Более детально технология описана в статье “От валютных пар к абсолютным курсам отдельных валют” (только в этой статье 2018 года дается транспонированное представление матриц преобразования в отличии от представления настоящей статьи).
Прямая матрица легко определяется. Строки в ней соответствуют валютам, а столбцы валютным парам. Матрица сильно разрежена и состоит из нулей, единиц и минус единиц.
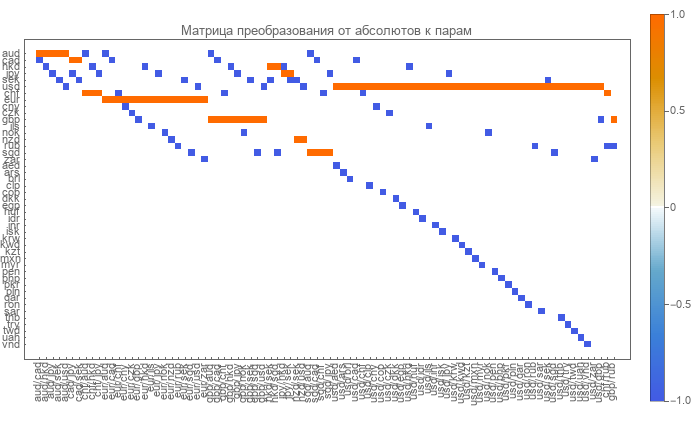
Нули говорят об отсутствии такой пары и валюты. Единица соответствует валюте в числителе пары. Минус единица обозначает валюту в знаменателе пары.
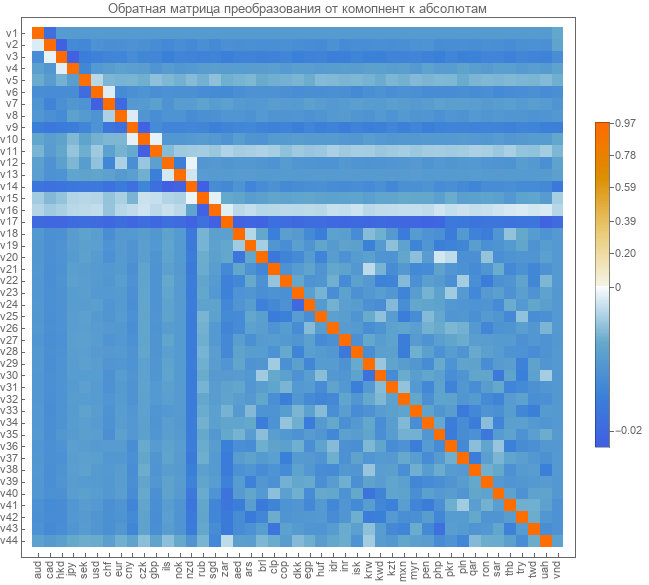
Обратная матрица преобразования от пар к абсолютным курсам не определена. Ее необходимо вычислять. Наиболее очевидный метод — это минимизировать ошибку восстановления парных курсов. Что и было сделано для вычисления этой матрицы в 2017 году. Приводим графическое представление этой матрицы.
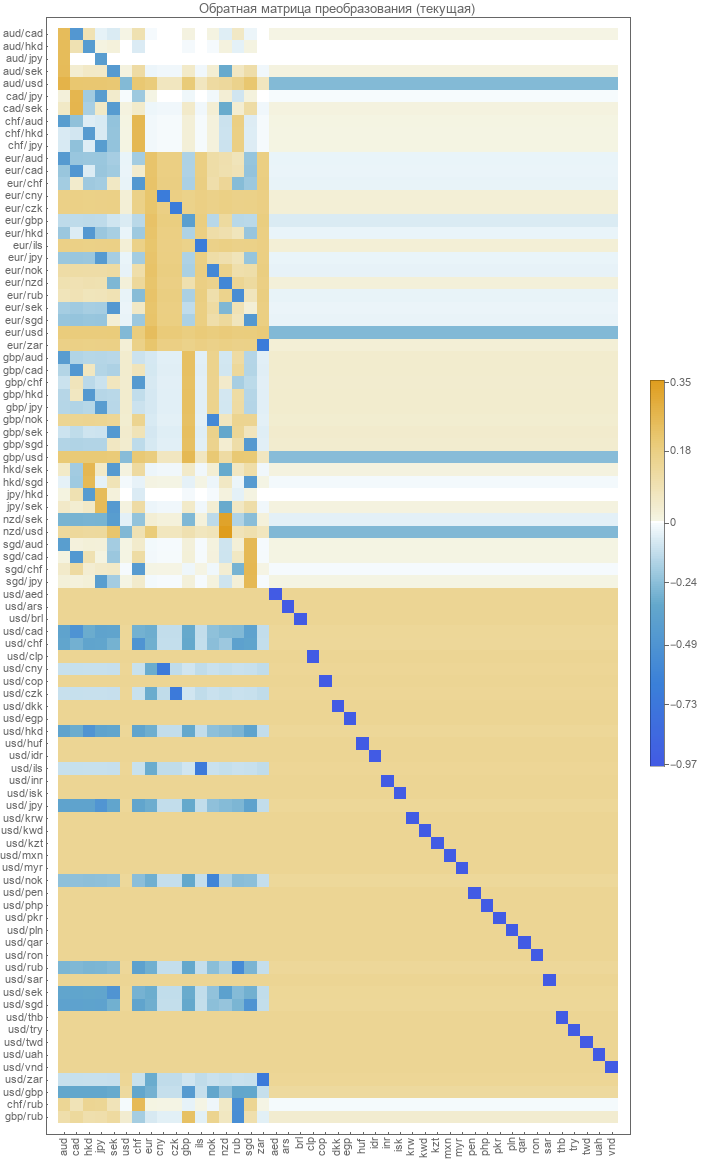
Проверка точности существующей модели
Для действующей матрицы были получены абсолютные и восстановленные парные валютные курсы. Были обнаружены резкие отличия между исходными и восстановленными парными курсами.
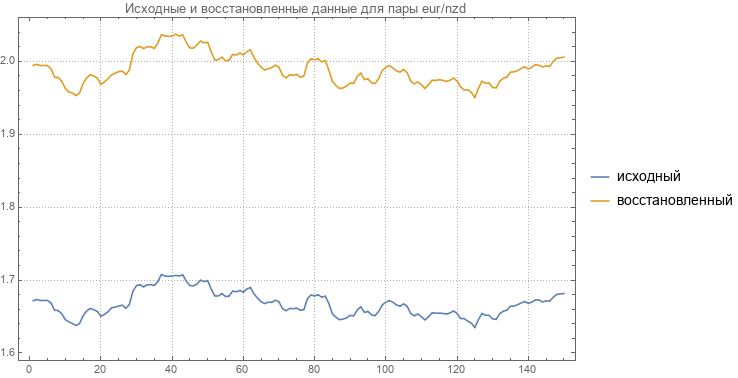
Далее был произведен расчет ошибок восстановления для всех пар.
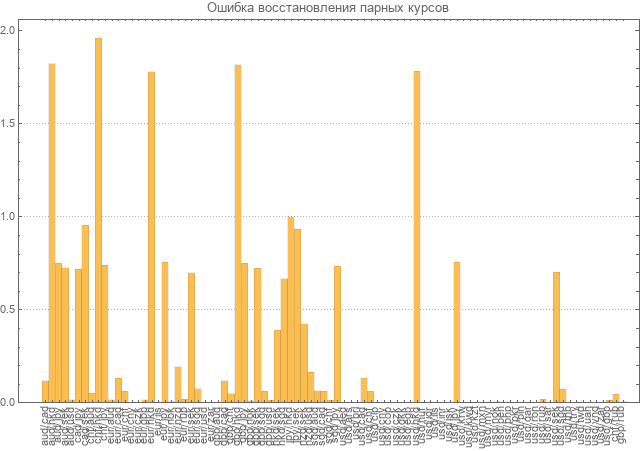
Ошибка считалась как среднее относительных отклонений взятых по модулю. Как можно видеть на диаграмме ошибки по многим парам почти в два раза больше самих значений.
Конечно такой уровень ошибки не позволяет считать модель состоятельной и требует пересчета.
Псевдообратная матрица от прямой
Первое что мы попробуем — это посчитаем просто обратную матрицу для матрицы прямого преобразования. Ввиду того что матрица у нас неквадратная придется использовать псевдообратное преобразование. Результат имеет следующий.
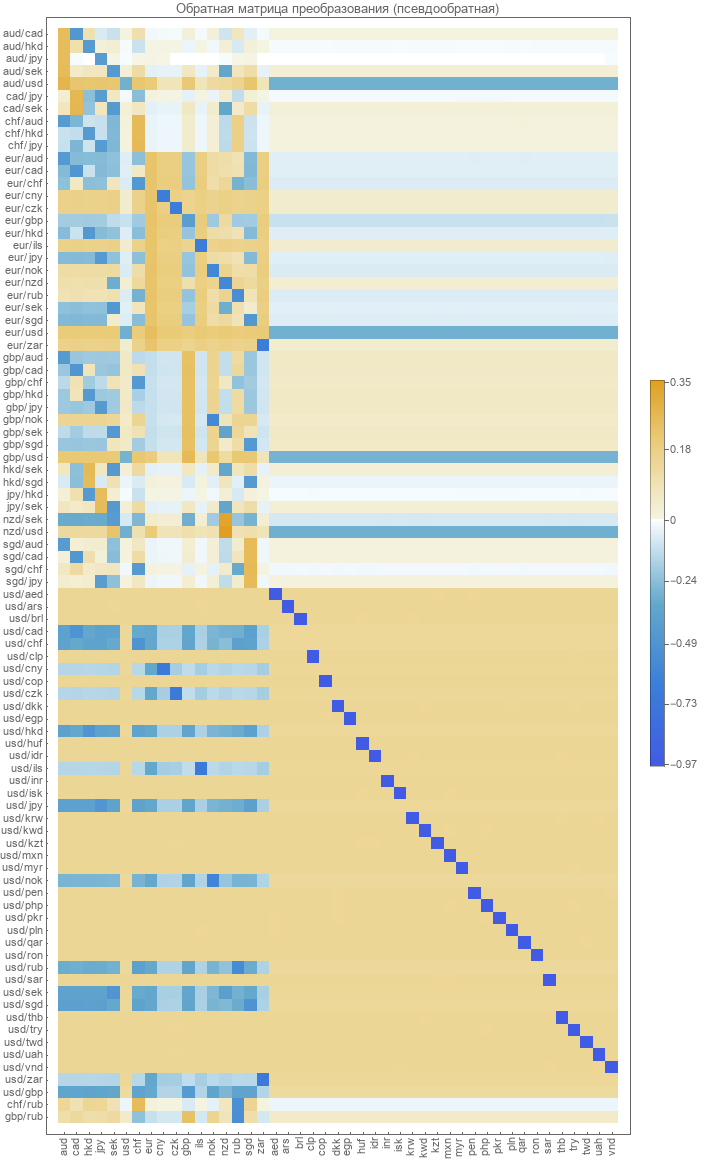
Очень похоже на то что мы получили ранее используя для оптимизации реальные парные курсы валют.
Рассчитаем абсолютные курсы. Затем восстановим из абсолютных парные курсы. Диаграмма ошибок получилась следующая.
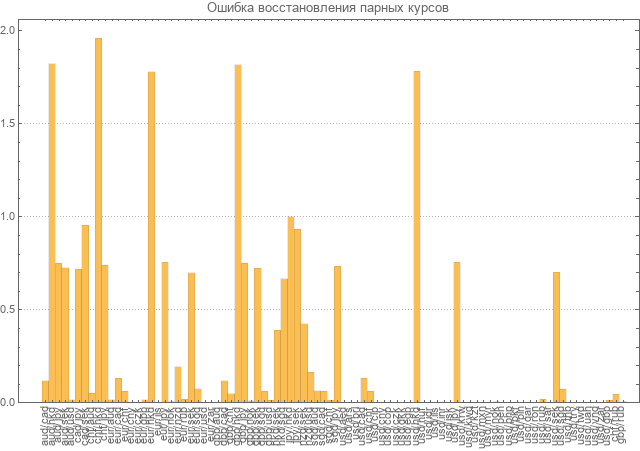
Ошибки тоже получились большие как и в оценке выше. Эта модель тоже не может нас устроить.
Расчет обратной матрицы через линейно независимые компоненты
Если детально проанализировать матрицу прямого преобразования, то можно обнаружить, что она имеет вырожденный вид (ранг матрицы меньше чем число строк-валют). Другими словами в прямой матрице есть линейно зависимые строки. И потому получить приемлемую обратную матрицу нам не получится.
Для выхода из сложившейся ситуации было предложено следующее решение. При переходе от абсолютных курсов к парным необходимо сначала переходить к линейно-независимым компонентам. И уже потом переходить к парам. Матрицы перехода от абсолютных курсов к компонентам и от компонент к парным курсам будут невырожденными и можно будет получить обратные матрицы.
Для поиска линейно-независимых компонент необходимо к матрице прямого преобразования присоединить единичную матрицу парных курсов. Таким образом мы получим две матрицы перехода от абсолютных курсов к парным и присоединенную матрицу перехода от парных к парным.
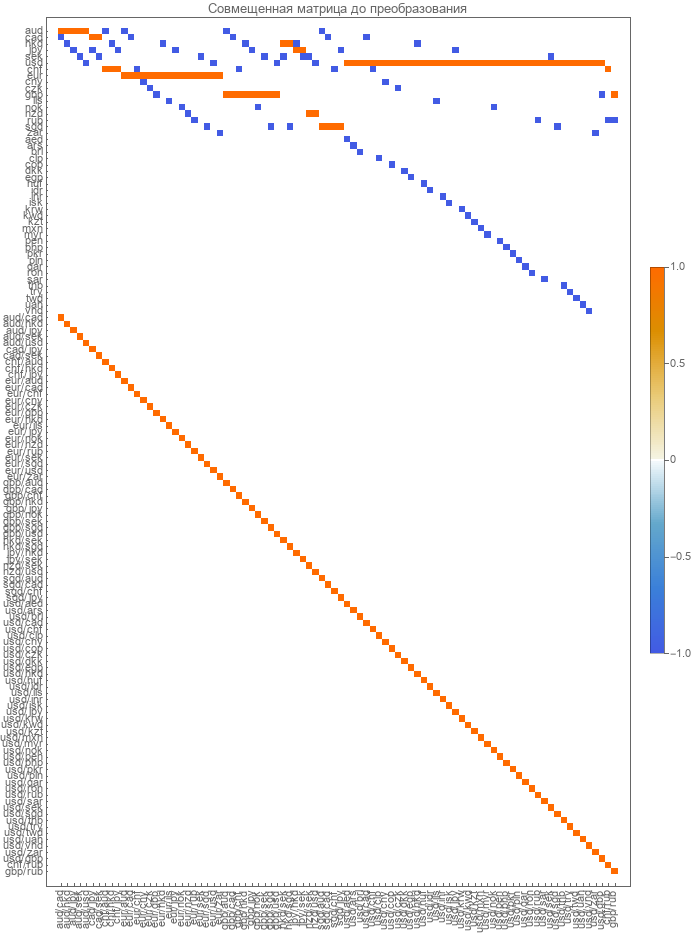
Теперь будем производить стандартные преобразования к ступенчатому виду верхней части этой совмещенной матрицы (на самом деле стандартные средства математического пакета Wolfram Mathematica приводят дальше к диагональному виду). В результате удалось получить следующую преобразованную матрицу.

Теперь в столбцах этой матрицы имеем линейно-независимые компоненты. Причем мы можем к ним перейти как от абсолютных курсов (верхняя часть матрицы) так и от парных курсов (нижняя часть совмещенной преобразованной матрицы).
Выделим эти матрицы перехода к линейно-независимым компонентам. Вот матрица перехода к компонентам от абсолютных курсов.
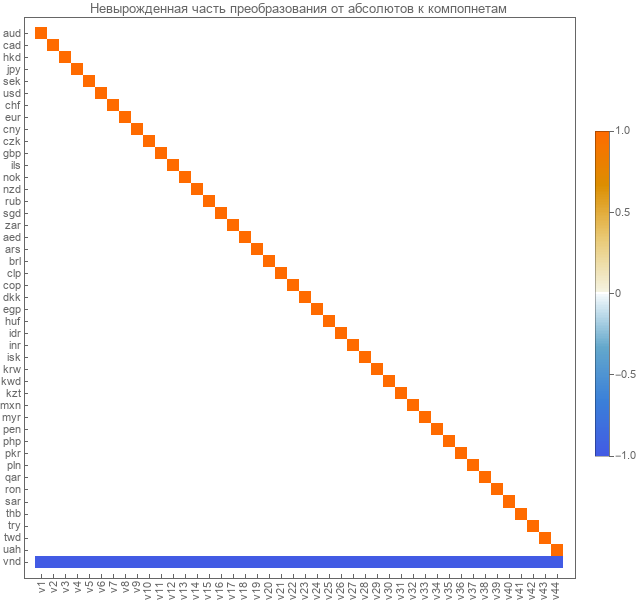
Вот матрица перехода от парных курсов к линейно-независимым компонентам.

Переход от абсолютов к компонентам происходит через рассчитанную выше матрицу. Обратное преобразование от компонент к абсолютам делаем через обратную матрицу. Ввиду того что она будет невырожденной можно получить хорошую обратную матрицу. Будем получать как псевдообратную. Вот ее вид.
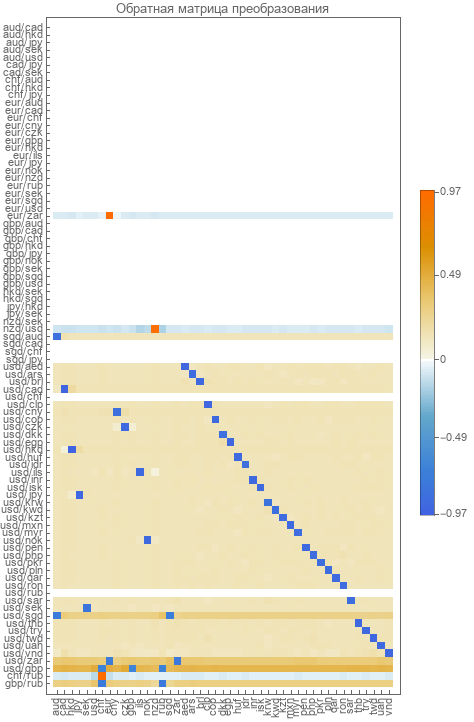
Теперь можно получить полную матрицу обратного преобразования от пар к абсолютам. Для этого умножим матрицу преобразования от пар к компонентам на обратную матрицу преобразования от компонент к абсолютам. Вид она имеет такой.
Хотя подобное мы уже видели выше, но все же матрица другая. Исследуем результаты которые она дает. Рассчитаем абсолютные курсы, а из них уже восстановим парные. Ошибка восстановления получилась следующая.
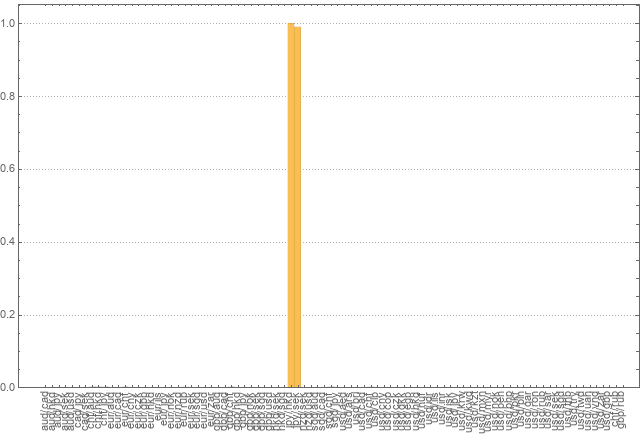
На всех парах кроме двух практически нулевые ошибки. Выясняем что с этими парами.
Оказывается в двух валютных парах неверные данные принимаются. Для jpy/hkd и jpy/sek данные идут лотами по 10000 и 100 шт. Необходимо исправить и заново проверить.
После исправлений входных парных курсов (избавления от лотов) и повторных вычислений абсолютных и восстановленных парных курсов смотрим ошибку восстановления.
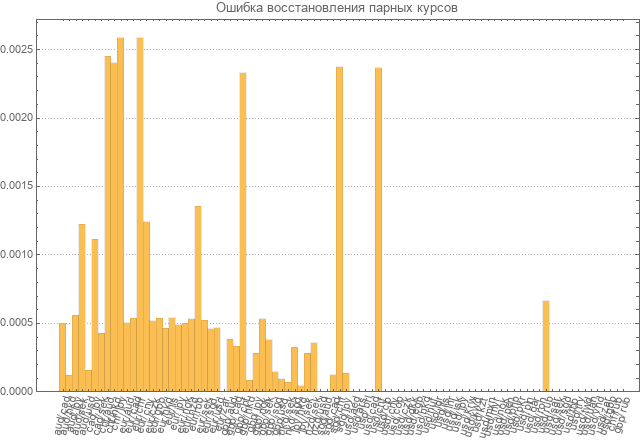
Получили ошибку в пределах 0.3%. Вполне приемлемый уровень ошибки.
Вот пример графика абсолютного курса.
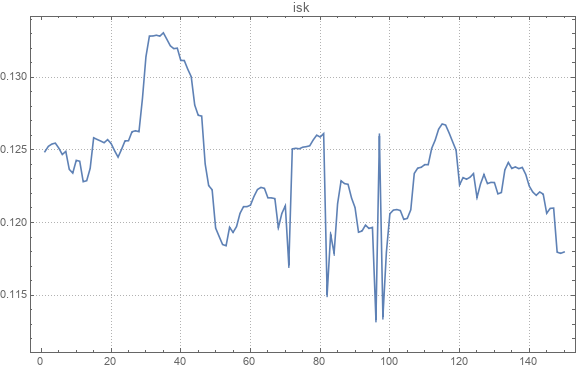
Вот пример исходного и восстановленного парных валютных курсов.
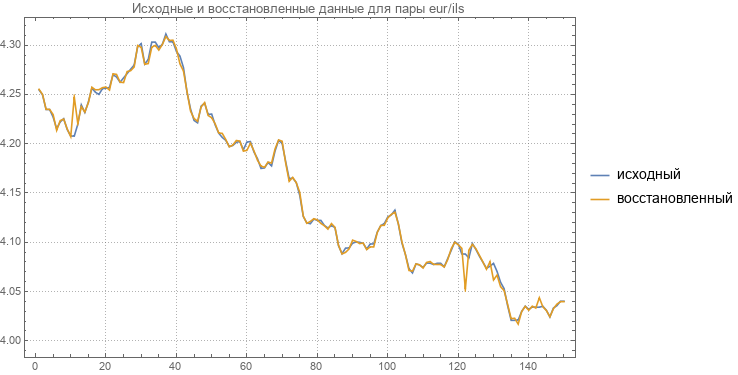
Раз уж пересчитали новую матрицу обратного преобразования снова приводим данные по последним абсолютным курсам всех участвующих валют.

Можно увидеть самую дорогую валюту. Это кувейтский динар стоимостью почти 47 абсов. Самая маленькая абсолютная стоимость у вьетнамского донга — 0.003 абса.
Выводы
В результате проведенных исследований выяснили, что существующий метод расчета абсолютных курсов дает существенную погрешность. Кроме того обнаружена ошибка в исходных данных.
Обратную матрицу преобразования от пар к абсолютам удалось получить лишь используя метод преобразования к меньшему количеству линейно-независимых компонент с невырожденной матрицей преобразования.
Метод получения обратной матрицы преобразования не использовал данные парных курсов. И потому от них независим.
Проверка преобразования на реальных курсах показала низкий уровень ошибки. Из чего был сделан вывод о применимости найденной матрицы обратного преобразования от парных валютных курсов к абсолютным.
Метод не претендует на статус законченного и математически выверенного, но как приемлемое решение будет применяется для дальнейших исследований свой абсолютных валютных курсов.
