В большинстве систем проектирования (САПР) основным представлением моделируемого объекта является граничное представление геометрии или B-rep (Boundary representation). Но все чаще пользователям САПР приходится иметь дело с полигональными моделями, например, полученными в результате 3D-сканирования или заимствованными из онлайн-каталогов.
Чтобы сделать их пригодными для дальнейшей работы, нужно конвертировать полигональную сетку в B-rep модель. А это совсем непросто.
Мы разработали программный компонент C3D B-Shaper, который встраивается в систему проектирования и преобразует полигональные модели в граничное представление. В этом посте покажем алгоритм конвертации и примеры реализации на С++.

В чем главная проблема полигональных моделей с точки зрения САПР? К ним нельзя применять традиционные инструменты – выполнять булевы операции, строить фаски и скругления, получать проекции и сечения. Если по B-rep модели построить ее полигональное представление достаточно легко (это делается с помощью триангуляции), то обратное преобразование сделать намного сложнее. Возникает целый ряд проблем – распознавание поверхностей различного типа (в том числе и поверхностей свободной формы), наличие шумов, которые свойственны, например, результатам 3D-сканирования.
В новом SDK мы реализовали трехступенчатый механизм конвертации полигональной модели в B-rep: сегментация, реконструкция поверхностей, построение модели B-rep. В общем случае процесс предполагается итерационным: если пользователя по каким-либо причинам не устраивает полученный результат, то он может внести необходимые корректирующие изменения на этапах сегментации и реконструкции поверхностей.
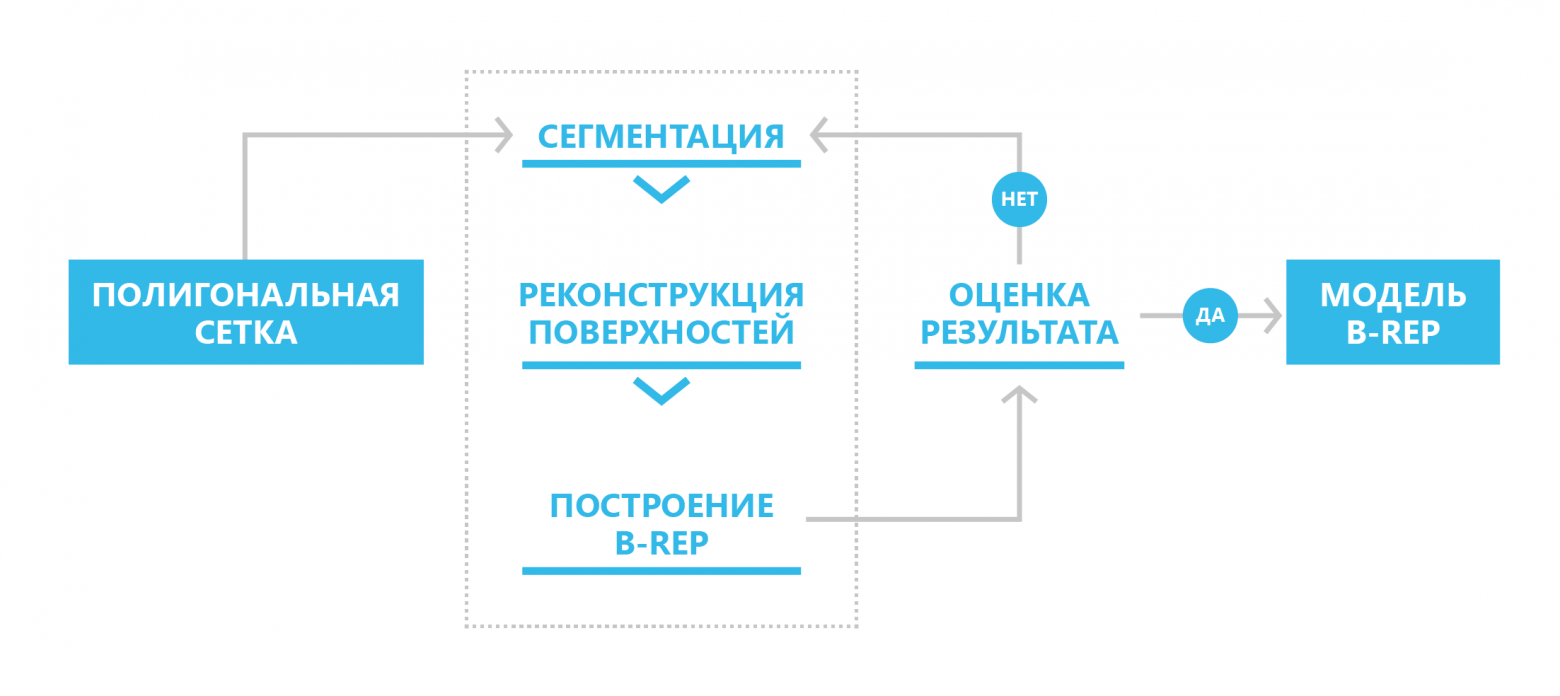
Схема преобразования полигонального представления в граничное
До инициирования процесса преобразования в B-rep необходимо, в некоторых случаях, улучшить качество исходной полигональной сетки: согласовать направления нормалей на соседних полигонах, устранить «дыры», применить алгоритмы сглаживания при наличии шумов в исходной сетке.
На первом этапе осуществляется классификация исходного множества полигонов сетки на подмножества (сегменты). Информация о нормалях в вершинах сетки позволяет произвести сегментацию первого порядка и тем самым обеспечить начальное разбиение сетки, а также классифицировать плоские или сильно изогнутые области.
Начальное разбиение сетки основано на определении так называемых «острых» ребер — таких ребер между двумя треугольными полигонами, угол между средними нормалями которых превышает некоторое, заранее заданное значение.
Сегментация второго порядка анализирует сетку в соответствии с ее главными кривизнами, что обеспечивает достаточный фундамент для классификации элементарных поверхностей. При расчете кривизн в вершинах сетки использовались результаты работы Майера (Mark Meyer, Mathieu Desbrun, Peter Schroder, and Alan H. Barr, «Discrete Differential-Geometry Operators for Triangulated 2-Manifolds», Visualization and Mathematics III, 2003) по определению дискретного дифференциального оператора для триангулированных областей: для каждой вершины исходной сетки рассматривается набор соседних вершин, связанных с данной через ребро. Затем для данной вершины рассчитывается дискретный оператор K, на основе которого определяются средняя нормаль, средняя KH и Гауссова KG кривизны в вершине сетки.
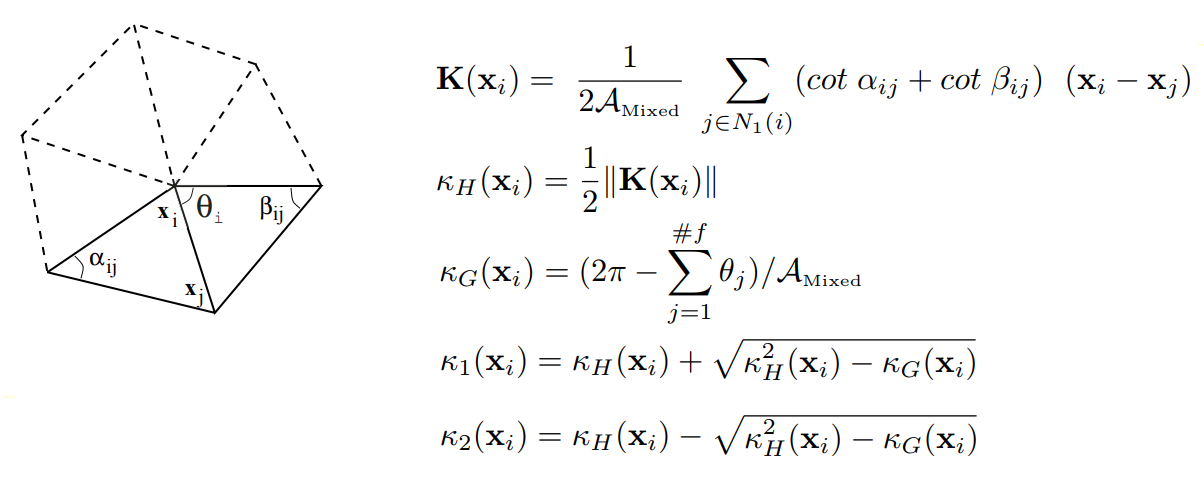
К определению дискретного дифференциального оператора для триангулированных областей
Таким образом вычисляется тензор кривизн для каждой вершины сетки, собственными числами которого являются искомые главные кривизны K1 и K2, а собственными векторами – главные направления изменения кривизн.
Далее производится классификация вершин сетки согласно рассчитанным в них значениям главных кривизн K1 и K2. Алгоритм классификации вершин основан на методе k-средних, т. е. на минимизации суммарного квадратичного отклонения точек кластеров от центров этих кластеров. В результате на выходе алгоритма каждая вершина сетки ассоциирована с некоторым кластером и парой кривизн (центр кластера)(L. Guillaume, «Curvature Tensor Based Triangle Mesh Segmentation with Boundary Rectification», Proceedings Computer Graphics International(CGI), 2004).
и парой кривизн (центр кластера)(L. Guillaume, «Curvature Tensor Based Triangle Mesh Segmentation with Boundary Rectification», Proceedings Computer Graphics International(CGI), 2004).
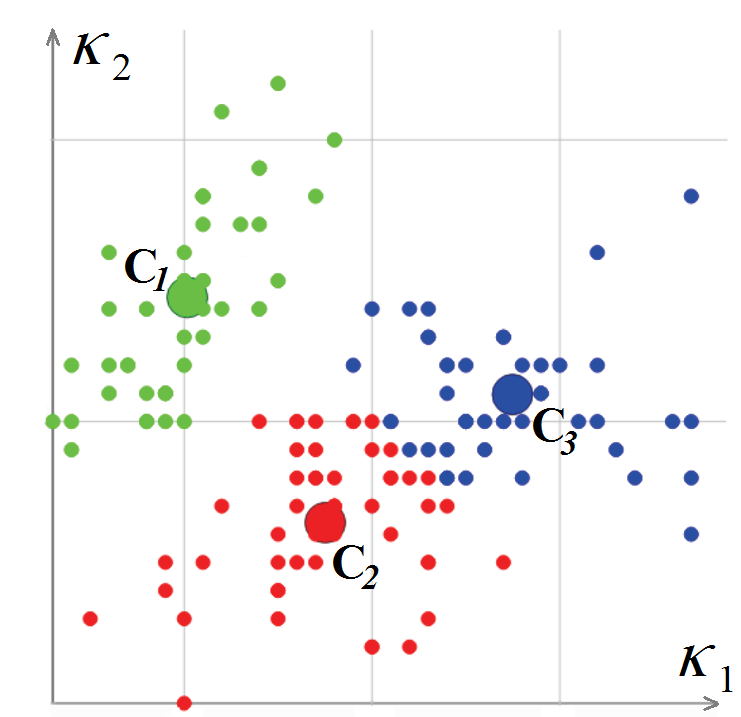
Классификация вершин полигональной сетки в пространстве кривизн
После классификации вершин полигональной сетки необходимо классифицировать полигоны. В начале этой процедуры выбирается треугольный полигон, для которого кривизна может считаться полностью определенной (все три вершины принадлежат одному кластеру либо две вершины лежат на остром ребре). Этот полигон объявляется новым сегментом, и с него стартует рекурсивная процедура расширения сегмента: для каждого треугольного полигона рассматриваются соседние к нему полигоны при условии, что ребро между ними не «острое».
В случае, если вершина соседнего полигона, противолежащая общему ребру, лежит на остром ребре либо принадлежит тому же кластеру, то этот полигон добавляется в сегмент. Процесс повторяется до тех пор, пока все полигоны данной сетки не будут просмотрены. Вот как выглядит реализованный механизм сегментации полигональной сетки.
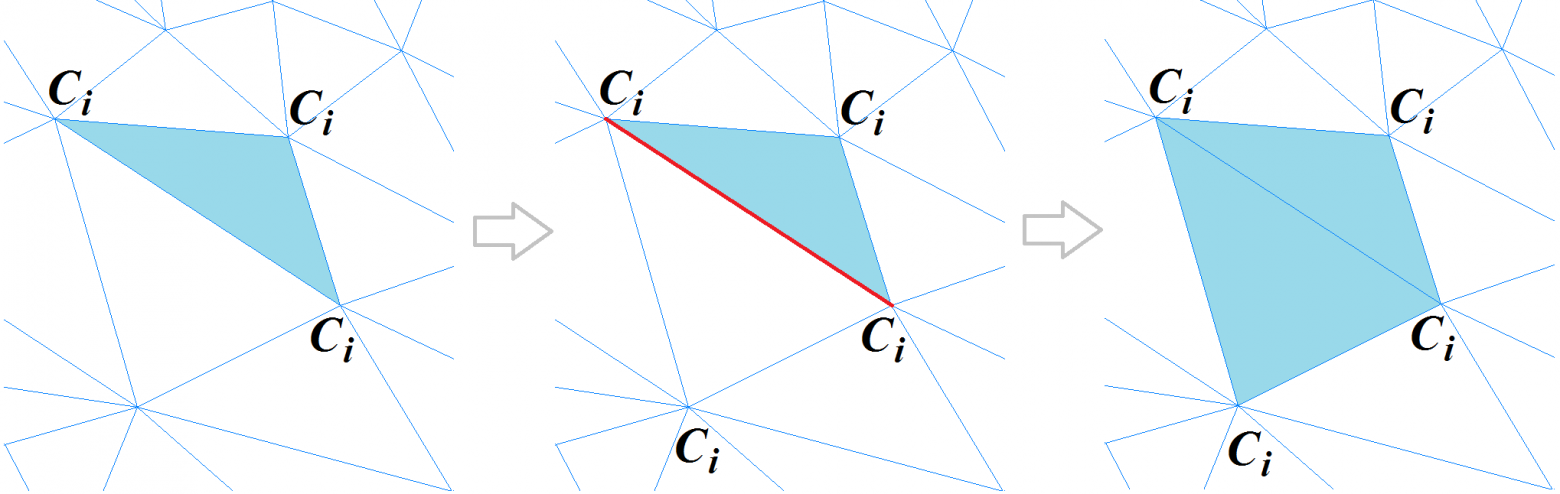
Механизм сегментации полигональной сетки
По окончании процедуры формирования сегментов выполняется специальный алгоритм сшивки соседних сегментов для устранения излишней сегментации рассматриваемой сетки.
На втором этапе каждому из сегментов необходимо поставить в соответствие некоторую поверхность, аппроксимирующую его форму с заданной точностью. Прежде всего, по значениям главных кривизн для данного сегмента определяется возможность описания формы сегмента элементарной поверхностью:
В случае если ни одна из элементарных поверхностей не подходит для описания сегмента, алгоритм будет пытаться распознать поверхность выдавливания или вращения. В конечном счете, если не удалось подобрать аналитическую поверхность для описания формы сегмента, для него будет строиться NURBS поверхность.
Элементарные поверхности строятся с помощью методов вписывания простых геометрических объектов в множество точек. Так, для вписывания окружности и сферы используется метод наименьших квадратов, для вписывания плоскости – метод главных компонент. Каждая реконструированная поверхность проверяется на соответствие сегменту по заданной точности распознавания.
Для наглядности мы раскрасили распознанные поверхности в разные цвета: плоскости – синие, цилиндры – красные, сферы — зеленые, конусы — желтые, торы — фиолетовые.

Исходная полигональная сетка (слева) и сегментированная сетка (справа) с распознанными на сегментах поверхностями
Финальным этапом преобразования является построение на основе сегментации распознанных поверхностей модели B-rep. При этом подходе на основе сегментированных областей строится граф смежных областей, который отражает топологию модели и служит основой для построения окончательной модели B-rep.
В отличие от предыдущих этапов преобразования, сборка B-rep выполняется в полностью автоматическом режиме: находятся линии пересечения соседних реконструированных поверхностей, на их основе строятся ребра граней, сами грани и, в завершении, собирается оболочка B-rep.


Исходная полигональная сетка (слева) и модель B-rep (справа)
Однако, топологически корректную оболочку удается построить не всегда. В качестве примера такой ситуации предположим, что в ходе реконструкции поверхностей у нас имеются две поверхности — цилиндр и плоскость, причем положение их в пространстве близко к касательному. Из-за погрешностей реконструкции поверхностей их пересечения может и не быть вообще. В таких случаях оболочка может построиться с некоторыми дефектами, которые пользователь может исправить, скорректировав должным образом параметры поверхностей.
На сегодняшний день можно выделить несколько основных источников моделей в полигональном представлении:
Полигональные модели из этих источников можно условно разделить на две группы: в первую входят модели, которые являются триангуляцией B-rep объектов, а во вторую – все остальные. Характерные отличия первой группы – отсутствие шумов в полигональной сетке и преобладание аналитически заданных поверхностей. Таким образом, преобразование в B-rep моделей из первой группы будет проходить либо в полностью автоматическом режиме, либо с минимальным вмешательством пользователя.
Полигональные сетки моделей второй группы предполагают более плотное интерактивное взаимодействие с пользователем. Поэтому изначально мы заложили в C3D B-Shaper два режима работы – полностью автоматический и интерактивный.
Выбор тот или иного режима зависит еще и от цели преобразования: в некоторых случаях топологической связностью элементов получаемой оболочки, а также ее корректностью допустимо пренебречь. Такой подход допустим, например, для оптимизации отрисовки в BIM-приложении, когда пользователь может добавлять произвольные предметы интерьера в текущую модель помещения. С другой стороны, для задач реверс-инжиниринга необходимо получить как можно более точную копию исходной модели, например, с заданной точностью соблюсти соосность цилиндров, обеспечить касательное расположение пары поверхностей и в результате получить корректную топологию модели — в таком случае не обойтись без вмешательства пользователя в процесс преобразования.
Интерфейс автоматического преобразования C3D B-Shaper представлен следующими функциями, которые принимают на вход исходную сетку и настройки преобразования:
К настройкам преобразования относится значение точности распознавания, т.е. максимально допустимого отстояния вершин полигональной сетки в границах данного сегмента до распознаваемой поверхности. Эта точность может быть абсолютной или относительной: при использовании относительной точности отклонение граней тела от сетки проверяется относительно размера модели.
Также пользователю доступна опция переключения режимов распознавания, которая позволяет управлять типами поверхностей при реконструкции.
Расширенные возможности по управлению процессами сегментации и распознавания поверхностей предоставляет интерфейс класса MbMeshProcessor:
Например, для коррекции результатов автоматической сегментации предусмотрены инструменты объединения сегментов, их разделения и т.д. Пользователь может вписать в сегмент поверхность заданного типа, а также изменить параметры для уже распознанной поверхности.
В июле мы выпустили первую версию компонента и сейчас продолжаем разработку по нескольким направлениям: алгоритмы автоматической сегментации, инструменты для редактирования сегментации, построение поверхностей свободной формы (NURBS) на базе сегмента, повышение качества сборки оболочек B-rep.
Заинтересованные разработчики могут протестировать C3D B-Shaper. Компонент предоставляется бесплатно на три месяца по заявке на нашем сайте.
 Автор — Андрей Туманин, к.т.н., математик-программист C3D Labs
Автор — Андрей Туманин, к.т.н., математик-программист C3D Labs
Чтобы сделать их пригодными для дальнейшей работы, нужно конвертировать полигональную сетку в B-rep модель. А это совсем непросто.
Мы разработали программный компонент C3D B-Shaper, который встраивается в систему проектирования и преобразует полигональные модели в граничное представление. В этом посте покажем алгоритм конвертации и примеры реализации на С++.

В чем главная проблема полигональных моделей с точки зрения САПР? К ним нельзя применять традиционные инструменты – выполнять булевы операции, строить фаски и скругления, получать проекции и сечения. Если по B-rep модели построить ее полигональное представление достаточно легко (это делается с помощью триангуляции), то обратное преобразование сделать намного сложнее. Возникает целый ряд проблем – распознавание поверхностей различного типа (в том числе и поверхностей свободной формы), наличие шумов, которые свойственны, например, результатам 3D-сканирования.
В новом SDK мы реализовали трехступенчатый механизм конвертации полигональной модели в B-rep: сегментация, реконструкция поверхностей, построение модели B-rep. В общем случае процесс предполагается итерационным: если пользователя по каким-либо причинам не устраивает полученный результат, то он может внести необходимые корректирующие изменения на этапах сегментации и реконструкции поверхностей.
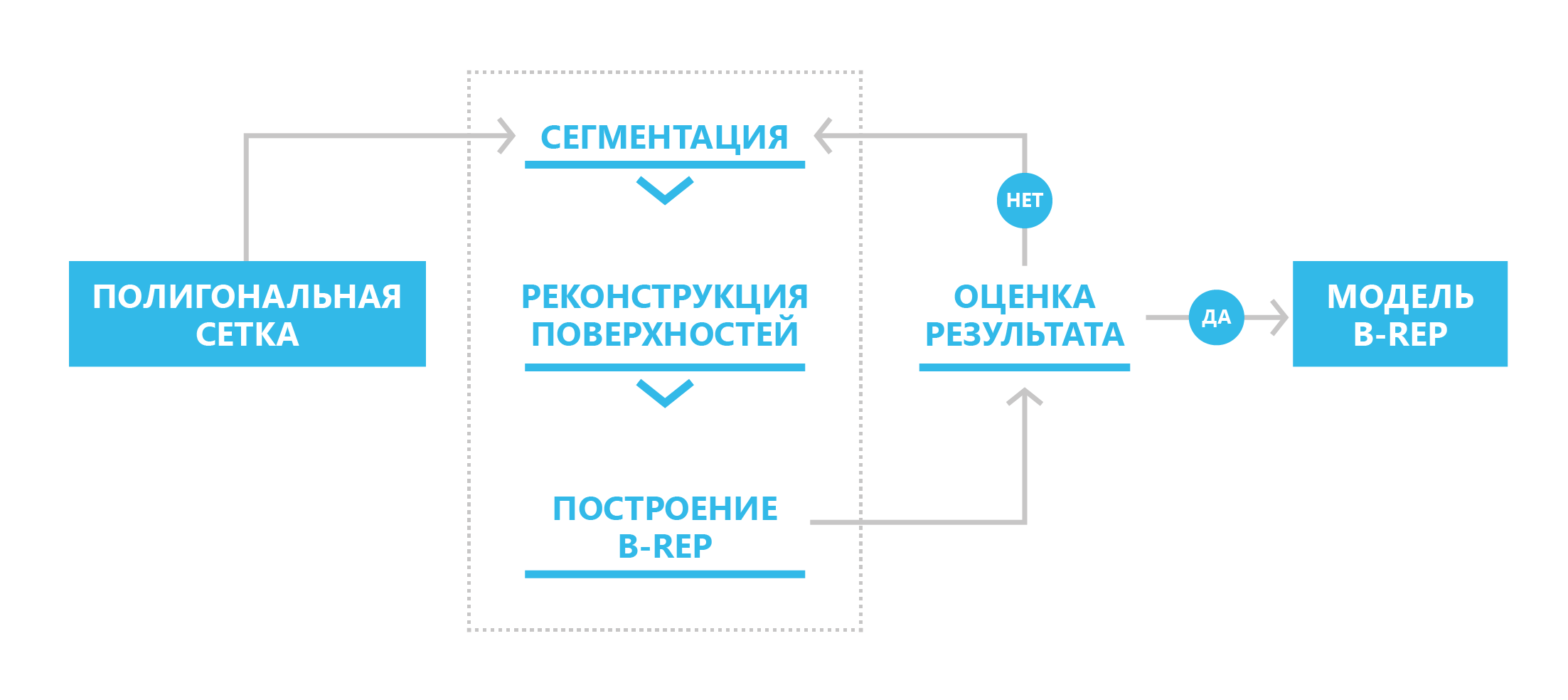
Схема преобразования полигонального представления в граничное
До инициирования процесса преобразования в B-rep необходимо, в некоторых случаях, улучшить качество исходной полигональной сетки: согласовать направления нормалей на соседних полигонах, устранить «дыры», применить алгоритмы сглаживания при наличии шумов в исходной сетке.
Сегментация полигональной модели
На первом этапе осуществляется классификация исходного множества полигонов сетки на подмножества (сегменты). Информация о нормалях в вершинах сетки позволяет произвести сегментацию первого порядка и тем самым обеспечить начальное разбиение сетки, а также классифицировать плоские или сильно изогнутые области.
Начальное разбиение сетки основано на определении так называемых «острых» ребер — таких ребер между двумя треугольными полигонами, угол между средними нормалями которых превышает некоторое, заранее заданное значение.
Сегментация второго порядка анализирует сетку в соответствии с ее главными кривизнами, что обеспечивает достаточный фундамент для классификации элементарных поверхностей. При расчете кривизн в вершинах сетки использовались результаты работы Майера (Mark Meyer, Mathieu Desbrun, Peter Schroder, and Alan H. Barr, «Discrete Differential-Geometry Operators for Triangulated 2-Manifolds», Visualization and Mathematics III, 2003) по определению дискретного дифференциального оператора для триангулированных областей: для каждой вершины исходной сетки рассматривается набор соседних вершин, связанных с данной через ребро. Затем для данной вершины рассчитывается дискретный оператор K, на основе которого определяются средняя нормаль, средняя KH и Гауссова KG кривизны в вершине сетки.
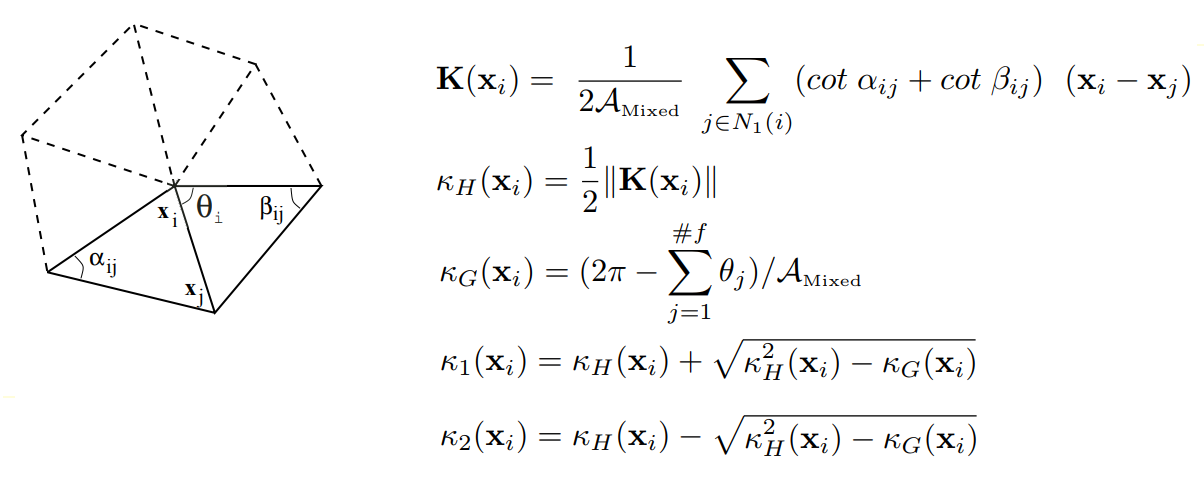
К определению дискретного дифференциального оператора для триангулированных областей
Таким образом вычисляется тензор кривизн для каждой вершины сетки, собственными числами которого являются искомые главные кривизны K1 и K2, а собственными векторами – главные направления изменения кривизн.
Далее производится классификация вершин сетки согласно рассчитанным в них значениям главных кривизн K1 и K2. Алгоритм классификации вершин основан на методе k-средних, т. е. на минимизации суммарного квадратичного отклонения точек кластеров от центров этих кластеров. В результате на выходе алгоритма каждая вершина сетки ассоциирована с некоторым кластером
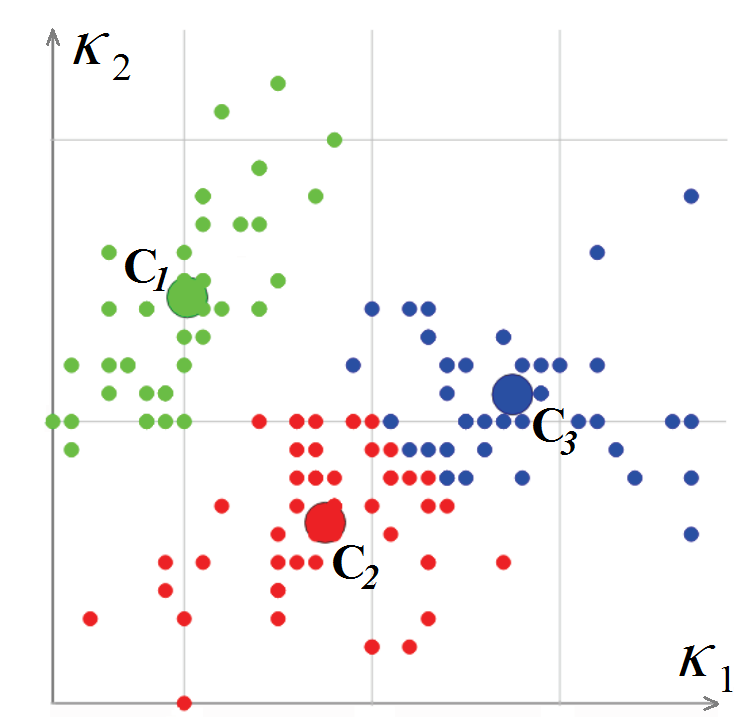
Классификация вершин полигональной сетки в пространстве кривизн
После классификации вершин полигональной сетки необходимо классифицировать полигоны. В начале этой процедуры выбирается треугольный полигон, для которого кривизна может считаться полностью определенной (все три вершины принадлежат одному кластеру либо две вершины лежат на остром ребре). Этот полигон объявляется новым сегментом, и с него стартует рекурсивная процедура расширения сегмента: для каждого треугольного полигона рассматриваются соседние к нему полигоны при условии, что ребро между ними не «острое».
В случае, если вершина соседнего полигона, противолежащая общему ребру, лежит на остром ребре либо принадлежит тому же кластеру, то этот полигон добавляется в сегмент. Процесс повторяется до тех пор, пока все полигоны данной сетки не будут просмотрены. Вот как выглядит реализованный механизм сегментации полигональной сетки.
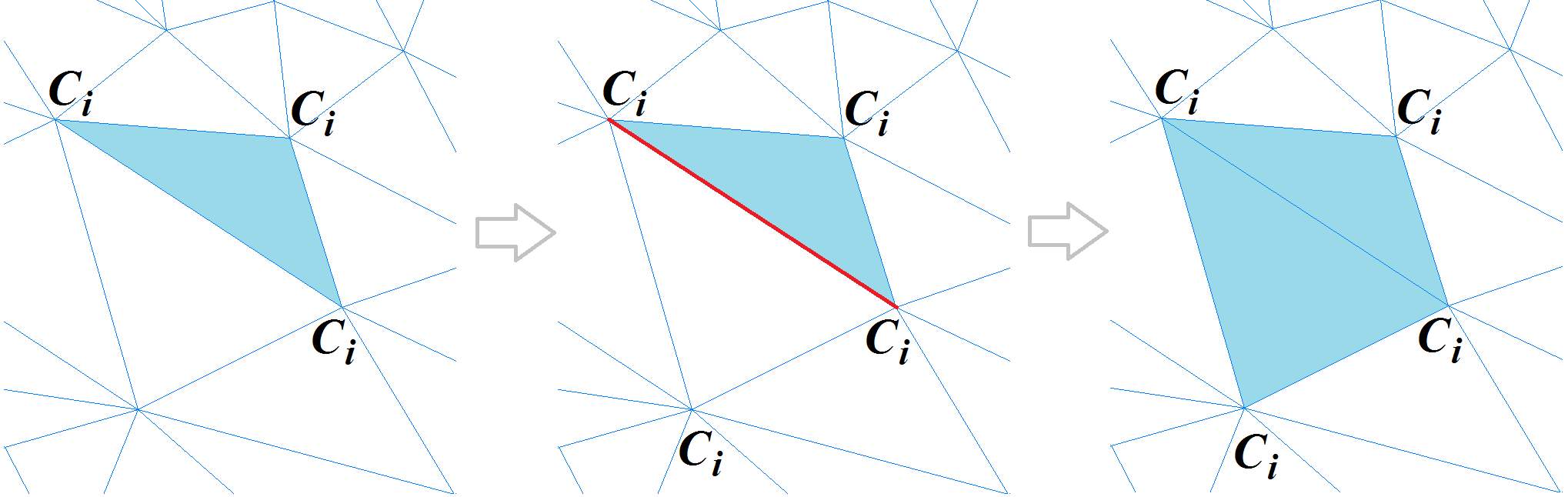
Механизм сегментации полигональной сетки
По окончании процедуры формирования сегментов выполняется специальный алгоритм сшивки соседних сегментов для устранения излишней сегментации рассматриваемой сетки.
Распознавание поверхностей
На втором этапе каждому из сегментов необходимо поставить в соответствие некоторую поверхность, аппроксимирующую его форму с заданной точностью. Прежде всего, по значениям главных кривизн для данного сегмента определяется возможность описания формы сегмента элементарной поверхностью:
- плоскость: k1 = k2 = 0
- сфера: k1 = k2 = K > 0
- цилиндр: k1 = K > 0, k2 = 0
- конус: k1 ∈ [a, b], k2 = 0
- тор:k1 = K, k2 ∈ [a, b]
В случае если ни одна из элементарных поверхностей не подходит для описания сегмента, алгоритм будет пытаться распознать поверхность выдавливания или вращения. В конечном счете, если не удалось подобрать аналитическую поверхность для описания формы сегмента, для него будет строиться NURBS поверхность.
Элементарные поверхности строятся с помощью методов вписывания простых геометрических объектов в множество точек. Так, для вписывания окружности и сферы используется метод наименьших квадратов, для вписывания плоскости – метод главных компонент. Каждая реконструированная поверхность проверяется на соответствие сегменту по заданной точности распознавания.
Для наглядности мы раскрасили распознанные поверхности в разные цвета: плоскости – синие, цилиндры – красные, сферы — зеленые, конусы — желтые, торы — фиолетовые.

Исходная полигональная сетка (слева) и сегментированная сетка (справа) с распознанными на сегментах поверхностями
Построение модели B-rep
Финальным этапом преобразования является построение на основе сегментации распознанных поверхностей модели B-rep. При этом подходе на основе сегментированных областей строится граф смежных областей, который отражает топологию модели и служит основой для построения окончательной модели B-rep.
В отличие от предыдущих этапов преобразования, сборка B-rep выполняется в полностью автоматическом режиме: находятся линии пересечения соседних реконструированных поверхностей, на их основе строятся ребра граней, сами грани и, в завершении, собирается оболочка B-rep.


Исходная полигональная сетка (слева) и модель B-rep (справа)
Однако, топологически корректную оболочку удается построить не всегда. В качестве примера такой ситуации предположим, что в ходе реконструкции поверхностей у нас имеются две поверхности — цилиндр и плоскость, причем положение их в пространстве близко к касательному. Из-за погрешностей реконструкции поверхностей их пересечения может и не быть вообще. В таких случаях оболочка может построиться с некоторыми дефектами, которые пользователь может исправить, скорректировав должным образом параметры поверхностей.
Типы полигональных моделей и выбор режима преобразования
На сегодняшний день можно выделить несколько основных источников моделей в полигональном представлении:
- онлайн-каталоги, базы данных 3D моделей в полигональном формате (STL, VRML, OBJ), например 3D Warehouse, Cults 3D и т. д
- результаты 3D-сканирования
- результаты топологической оптимизации моделей CAE-алгоритмами.
Полигональные модели из этих источников можно условно разделить на две группы: в первую входят модели, которые являются триангуляцией B-rep объектов, а во вторую – все остальные. Характерные отличия первой группы – отсутствие шумов в полигональной сетке и преобладание аналитически заданных поверхностей. Таким образом, преобразование в B-rep моделей из первой группы будет проходить либо в полностью автоматическом режиме, либо с минимальным вмешательством пользователя.
Полигональные сетки моделей второй группы предполагают более плотное интерактивное взаимодействие с пользователем. Поэтому изначально мы заложили в C3D B-Shaper два режима работы – полностью автоматический и интерактивный.
Выбор тот или иного режима зависит еще и от цели преобразования: в некоторых случаях топологической связностью элементов получаемой оболочки, а также ее корректностью допустимо пренебречь. Такой подход допустим, например, для оптимизации отрисовки в BIM-приложении, когда пользователь может добавлять произвольные предметы интерьера в текущую модель помещения. С другой стороны, для задач реверс-инжиниринга необходимо получить как можно более точную копию исходной модели, например, с заданной точностью соблюсти соосность цилиндров, обеспечить касательное расположение пары поверхностей и в результате получить корректную топологию модели — в таком случае не обойтись без вмешательства пользователя в процесс преобразования.
Интерфейс автоматического преобразования C3D B-Shaper представлен следующими функциями, которые принимают на вход исходную сетку и настройки преобразования:
MbResultType ConvertMeshToShell( MbMesh & mesh,
MbFaceShell *& shell,
const MbMeshProcessorValues & params );
MbResultType ConvertCollectionToShell( MbCollection & collection,
MbFaceShell *& shell,
const MbMeshProcessorValues & params );К настройкам преобразования относится значение точности распознавания, т.е. максимально допустимого отстояния вершин полигональной сетки в границах данного сегмента до распознаваемой поверхности. Эта точность может быть абсолютной или относительной: при использовании относительной точности отклонение граней тела от сетки проверяется относительно размера модели.
Также пользователю доступна опция переключения режимов распознавания, которая позволяет управлять типами поверхностей при реконструкции.
Расширенные возможности по управлению процессами сегментации и распознавания поверхностей предоставляет интерфейс класса MbMeshProcessor:
class MbMeshProcessor {
..
public:
// “Лечение” сетки.
void SetUseMeshSmoothing( bool useSmoothing );
// Управление сегментацией сетки.
const MbCollection & GetSegmentedMesh();
MbResultType SegmentMesh( bool createSurfaces = true );
void ResetSegmentation();
void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx );
MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep );
// Управление распознаванием поверхностей.
void FitSurfaceToSegment( size_t idxSegment );
void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType );
const MbSurface * GetSegmentSurface( size_t idxSegment ) const;
// Построение B-rep модели.
MbResultType CreateBRepShell( MbFaceShell *& pShell );
..
}Например, для коррекции результатов автоматической сегментации предусмотрены инструменты объединения сегментов, их разделения и т.д. Пользователь может вписать в сегмент поверхность заданного типа, а также изменить параметры для уже распознанной поверхности.
Что происходит сейчас
В июле мы выпустили первую версию компонента и сейчас продолжаем разработку по нескольким направлениям: алгоритмы автоматической сегментации, инструменты для редактирования сегментации, построение поверхностей свободной формы (NURBS) на базе сегмента, повышение качества сборки оболочек B-rep.
Заинтересованные разработчики могут протестировать C3D B-Shaper. Компонент предоставляется бесплатно на три месяца по заявке на нашем сайте.
 Автор — Андрей Туманин, к.т.н., математик-программист C3D Labs
Автор — Андрей Туманин, к.т.н., математик-программист C3D Labs






