Привет!
Тут мы опишем работу некоторого поля а затем сделаем пару красивых фичей (тут все ОЧЕНЬ просто).
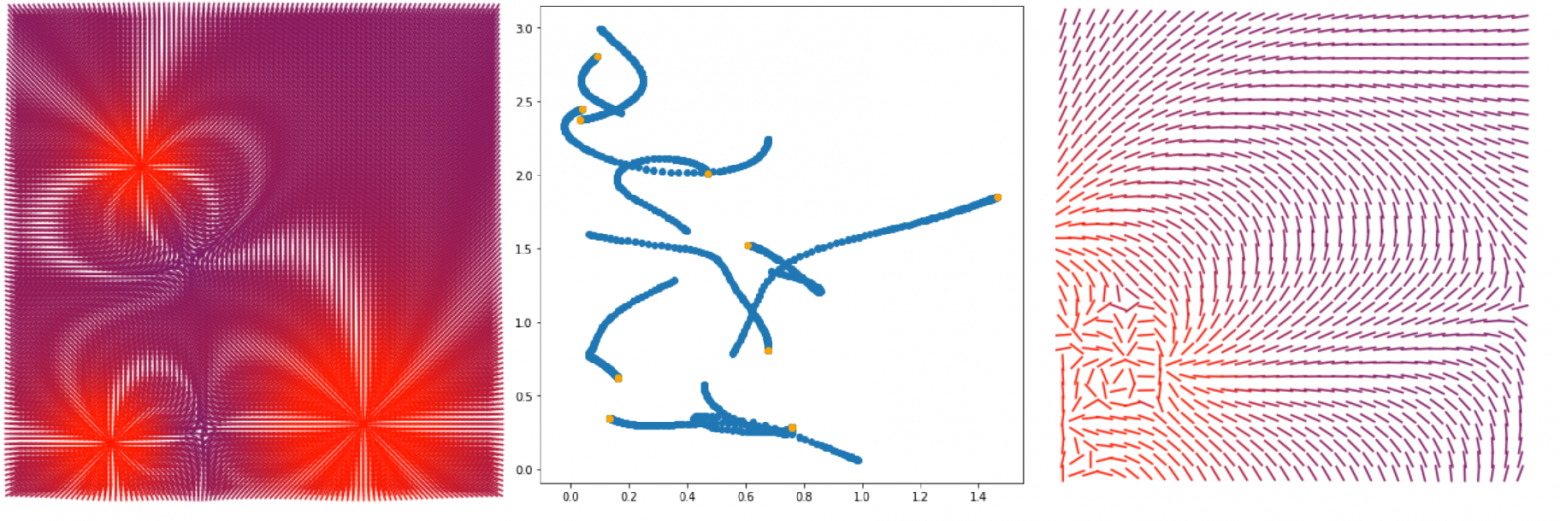
Что будет в этой статье.
Общий случай:
Частный случай (на основе общего):
Встретимся под катом!
Основа всех основ — вектор (особенно в нашем случае). Поэтому именно с описания вектора мы и начнем. Что нам нужно? Арифметические операции над вектором, расстояние, модуль, и пару технических вещей. Вектор мы будем наследовать от list. Так выглядит его инициализация:
То есть теперь мы можем создать вектор с помощью
Зададим арифметическую операцию сложение:
Отлично:
Аналогично зададим все арифметические операции (полный код вектора будет ниже). Теперь нужна функция расстояния. Я мог бы сделать деревенское dist(v1, v2) — но это не красиво, поэтому переопределим оператор %:
Отлично:
Еще нам нужна пара методов для более быстрого генерирования вектора и красивого выхода. Хитрого тут ничего нет, поэтому вот весь код класса Vector:
Тут по идее все просто — у точки есть координаты, скорость и ускорение (для простоты). Помимо этого у нее есть масса и набор кастомных параметров (к примеру для электромагнитного поля нам не помешает заряд, но вам никто не мешает задать хоть спин).
Инициализация будет такой:
А чтобы передвигать, обездвиживать и ускорять нашу точку напишем следующие методы:
Отлично, сама по себе точка сделана.
Полем взаимодействия мы зовем объект, включающий в себя множество всех материальных точек и оказывающий на них силу. Мы рассмотрим частный случай нашей замечательной вселенной, поэтому у нас будет одно кастомное взаимодействие (разумеется, это легко расширить). Объявим конструктор и добавление точки:
Теперь самое интересное — объявить функцию, которая возвращает «напряженность» в этой точке. Хотя это понятие относится к электромагнитному взаимодействию, в нашем случае это некоторый абстрактный вектор, вдоль которого мы и будем двигать точку. При этом у нас будет свойство точки q, в частном случае — заряд точки (в общем — что захотим, даже вектор). Итак, что такое напряженность в точке C? Что-то типа этого:
То есть напряженность в точке равна сумме сил всех материальных точек действующих на некоторую единичную точку.
равна сумме сил всех материальных точек действующих на некоторую единичную точку.
На этом моменте уже можно нарисовать векторное поле, но мы будем делать это в конце. Теперь сделаем шаг нашего взаимодействия
Тут все просто. Для каждой точки мы определяем напряженность в этих координатах а затем определяем конечную силу на ЭТУ материальную точку:
Определим недостающие функции.
Вот мы и дошли до самого интересного. Начнем с…
Вообще-то коэффициент k должен быть равен каким-то там миллиардам (9*10^(-9)), но так как он же будет гаситься временем t -> 0, я сразу решил сделать и то и другое адекватными числами. Поэтому в нашей физике k=300'000. А со всем остальным, думаю, понятно.
Далее мы добавляем десять точек (2-мерного пространства) с координатами от 0 до 10 по каждой из осей. Также, мы даем каждой точке заряд от -0.25 до 0.25. Теперь сделаем цикл и нарисуем точки по их координата (и следы):
Что должно было получиться:
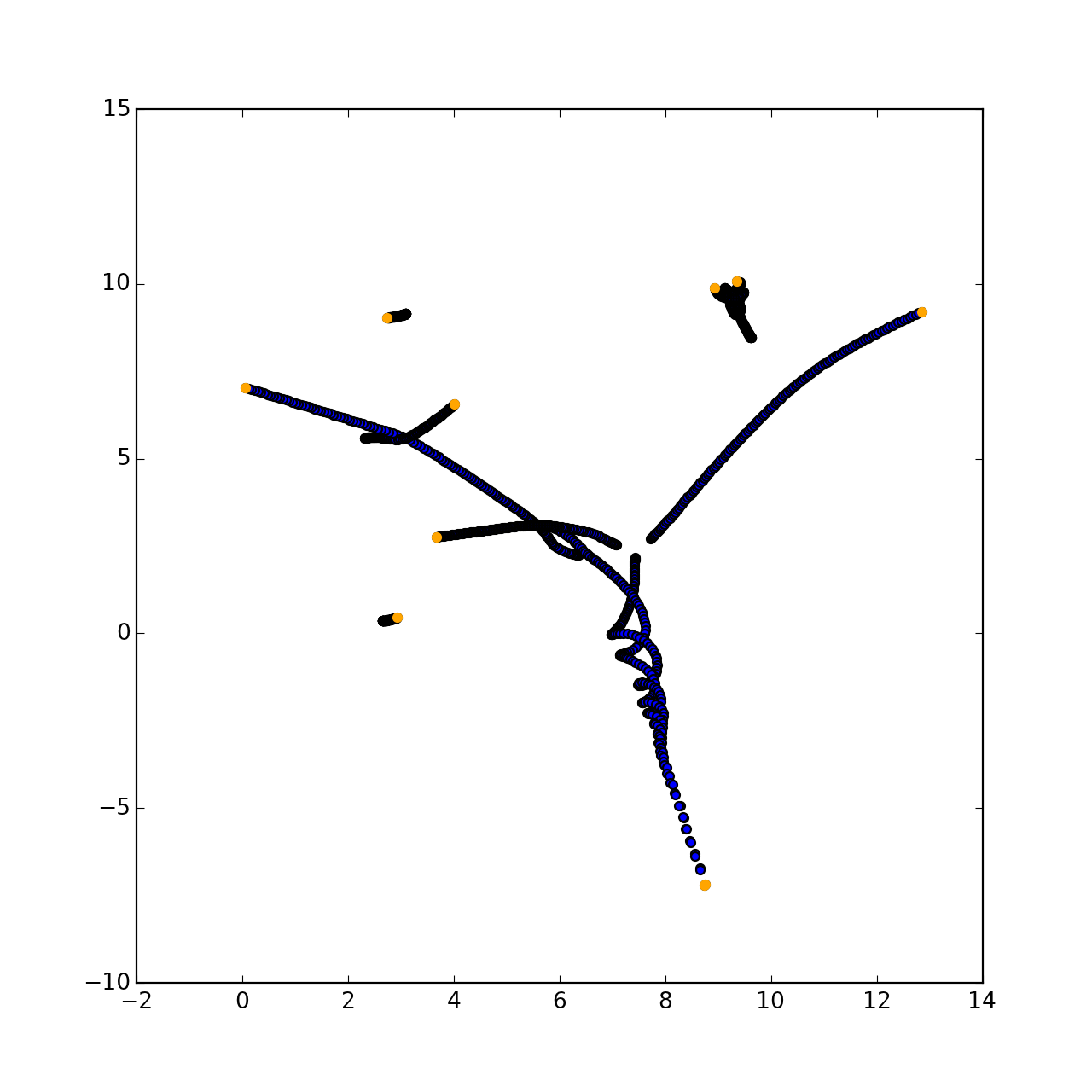
На самом деле рисунок там будет совершенно рандомный, ведь траектория каждой точки непредсказуема на данный момент развития механики.
Тут все просто. Нам нужно пройтись по координатам с каким-то шагом и нарисовать в каждых из них вектор в нужном направлении.
Примерно такой вывод должен был получиться.
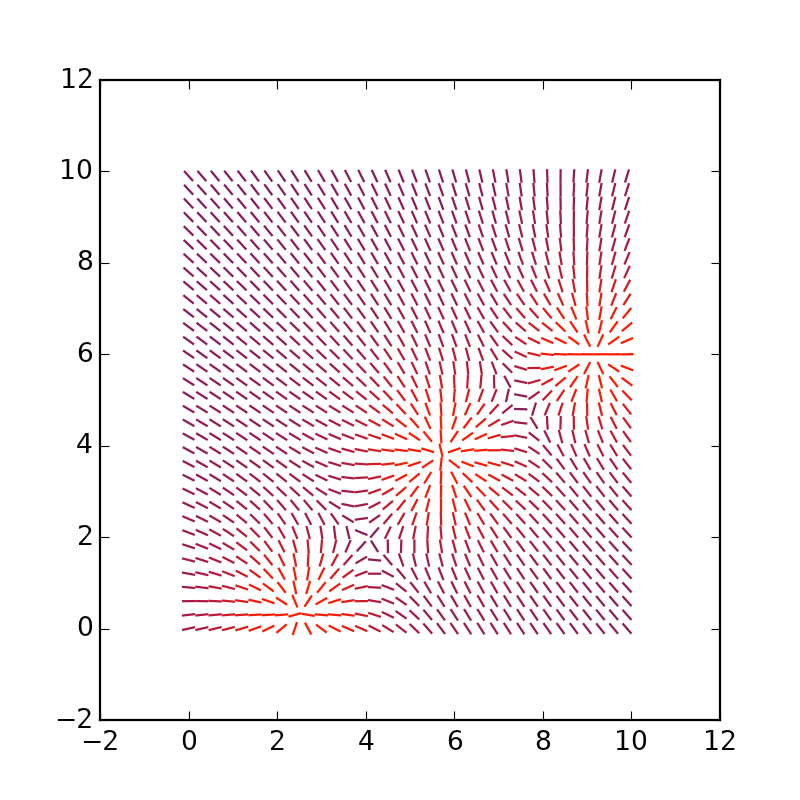
Можно удлинить сами векторы, заменим * 4 на * 1.5:
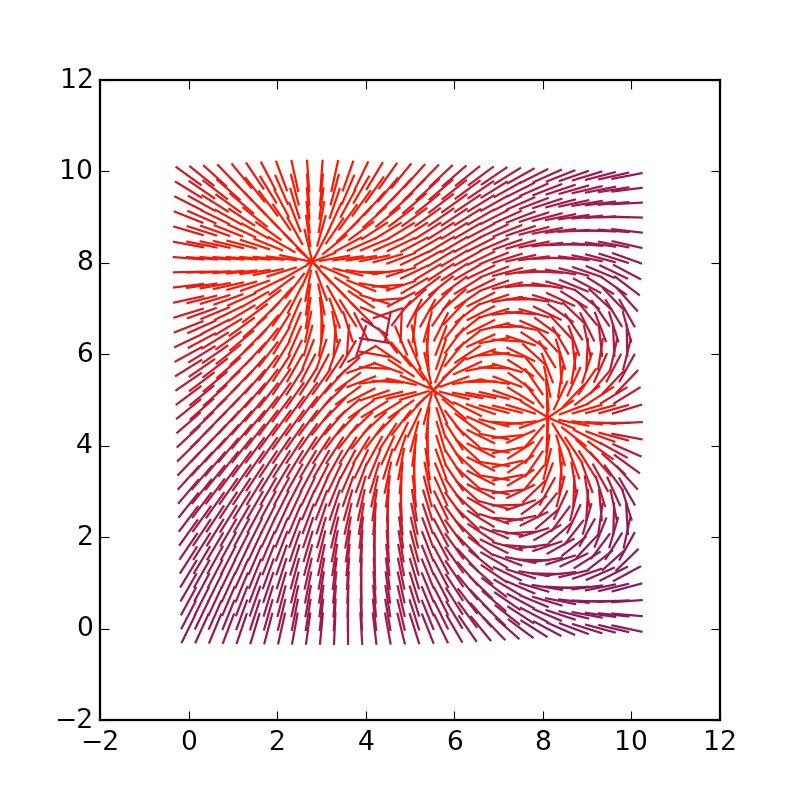
Создадим пятимерное пространство с 200 точек и взаимодействием, зависимым не от квадрата расстояния, а от 4-ой степени.
Теперь все координаты, скорости и т. д. определены в пяти измерениях. Теперь что-нибудь помоделируем:
Это — график суммы всех скоростей в каждый момент времени. Как видите, со временем они потихоньку ускоряются.
Ну вот это была коротенькая инструкция как сделать такую простую штуку. А вот что бывает, если поиграться с цветами:
Следующая статья будет возможно о более сложном моделировании, а быть может и флюидах и уравнениях Навье-Стокса.
UPD: Статья написана моим коллегой тут
Спасибо MomoDev за помощь в рендеринге видео.
Тут мы опишем работу некоторого поля а затем сделаем пару красивых фичей (тут все ОЧЕНЬ просто).
Что будет в этой статье.
Общий случай:
- Опишем базу, а именно работу с векторами (велосипед для тех, у кого нет под рукой numpy)
- Опишем материальную точку и поле взаимодействия
Частный случай (на основе общего):
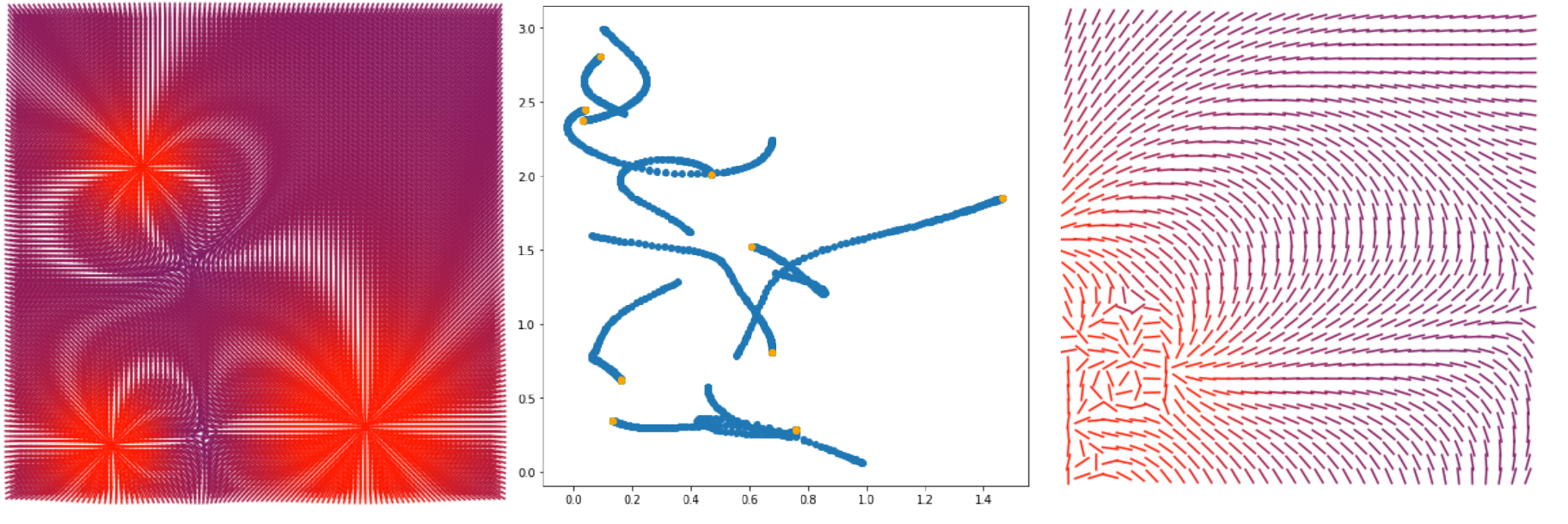
- Сделаем визуализацию векторного поля напряженности электромагнитного поля (первая и третья картинки)
- Сделаем визуализацию движения частиц в электромагнитном поле
Встретимся под катом!
Программирование теоретических основ
Вектор
Основа всех основ — вектор (особенно в нашем случае). Поэтому именно с описания вектора мы и начнем. Что нам нужно? Арифметические операции над вектором, расстояние, модуль, и пару технических вещей. Вектор мы будем наследовать от list. Так выглядит его инициализация:
class Vector(list):
def __init__(self, *el):
for e in el:
self.append(e)
То есть теперь мы можем создать вектор с помощью
v = Vector(1, 2, 3)
Зададим арифметическую операцию сложение:
class Vector(list):
...
def __add__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] + other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self + other
Отлично:
v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 + v2
>>> [3, 59, 26.2]
Аналогично зададим все арифметические операции (полный код вектора будет ниже). Теперь нужна функция расстояния. Я мог бы сделать деревенское dist(v1, v2) — но это не красиво, поэтому переопределим оператор %:
class Vector(list):
...
def __mod__(self, other):
return sum((self - other) ** 2) ** 0.5
Отлично:
v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 % v2
>>> 58.60068258988115
Еще нам нужна пара методов для более быстрого генерирования вектора и красивого выхода. Хитрого тут ничего нет, поэтому вот весь код класса Vector:
Весь код класса Vector
class Vector(list):
def __init__(self, *el):
for e in el:
self.append(e)
def __add__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] + other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self + other
def __sub__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] - other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self - other
def __mul__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] * other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self * other
def __truediv__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] / other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self / other
def __pow__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] ** other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self ** other
def __mod__(self, other):
return sum((self - other) ** 2) ** 0.5
def mod(self):
return self % Vector.emptyvec(len(self))
def dim(self):
return len(self)
def __str__(self):
if len(self) == 0:
return "Empty"
r = [str(i) for i in self]
return "< " + " ".join(r) + " >"
def _ipython_display_(self):
print(str(self))
@staticmethod
def emptyvec(lens=2, n=0):
return Vector(*[n for i in range(lens)])
@staticmethod
def randvec(dim):
return Vector(*[random.random() for i in range(dim)])
Материальная точка
Тут по идее все просто — у точки есть координаты, скорость и ускорение (для простоты). Помимо этого у нее есть масса и набор кастомных параметров (к примеру для электромагнитного поля нам не помешает заряд, но вам никто не мешает задать хоть спин).
Инициализация будет такой:
class Point:
def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties):
self.coords = coords
if speed is None:
self.speed = Vector(*[0 for i in range(len(coords))])
else:
self.speed = speed
self.acc = Vector(*[0 for i in range(len(coords))])
self.mass = mass
self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
self.q = q
for prop in properties:
setattr(self, prop, properties[prop])
А чтобы передвигать, обездвиживать и ускорять нашу точку напишем следующие методы:
class Point:
...
def move(self, dt):
self.coords = self.coords + self.speed * dt
def accelerate(self, dt):
self.speed = self.speed + self.acc * dt
def accinc(self, force): # Зная сообщаемую силу мы получаем нужное ускорение
self.acc = self.acc + force / self.mass
def clean_acc(self):
self.acc = self.acc * 0
Отлично, сама по себе точка сделана.
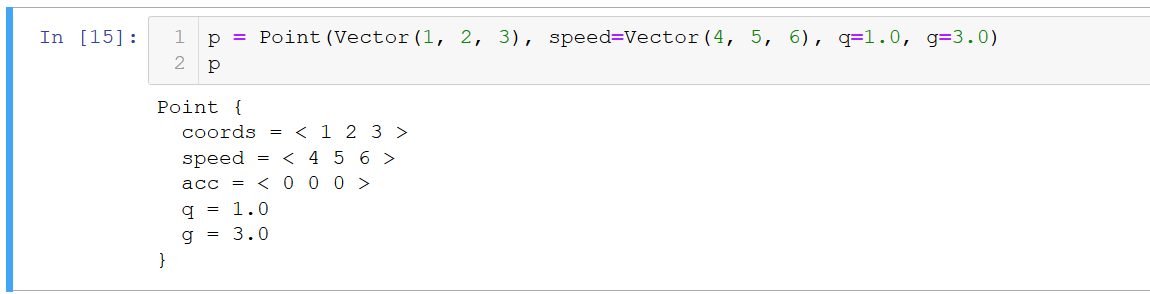
Код Point (с красивым выводом)
Результат:
class Point:
def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties):
self.coords = coords
if speed is None:
self.speed = Vector(*[0 for i in range(len(coords))])
else:
self.speed = speed
self.acc = Vector(*[0 for i in range(len(coords))])
self.mass = mass
self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
self.q = q
for prop in properties:
setattr(self, prop, properties[prop])
def move(self, dt):
self.coords = self.coords + self.speed * dt
def accelerate(self, dt):
self.speed = self.speed + self.acc * dt
def accinc(self, force):
self.acc = self.acc + force / self.mass
def clean_acc(self):
self.acc = self.acc * 0
def __str__(self):
r = ["Point {"]
for p in self.__params__:
r.append(" " + p + " = " + str(getattr(self, p)))
r += ["}"]
return "\n".join(r)
def _ipython_display_(self):
print(str(self))
Результат:
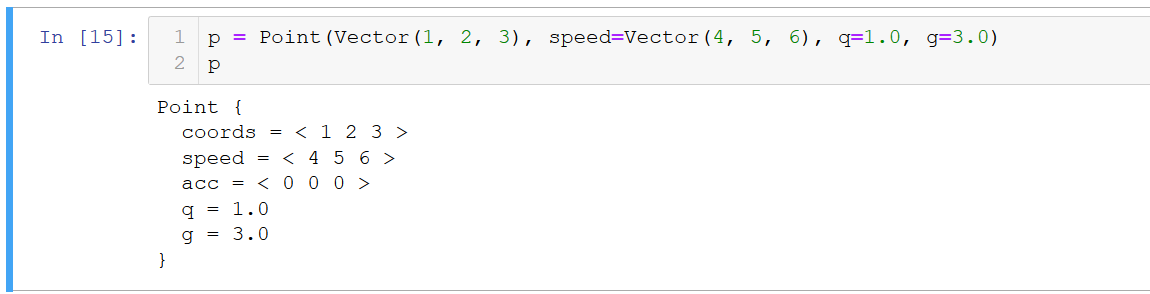
Поле взаимодействия
Полем взаимодействия мы зовем объект, включающий в себя множество всех материальных точек и оказывающий на них силу. Мы рассмотрим частный случай нашей замечательной вселенной, поэтому у нас будет одно кастомное взаимодействие (разумеется, это легко расширить). Объявим конструктор и добавление точки:
class InteractionField:
def __init__(self, F): # F - это кастомное взаимодействие, F(p1, p2, r), p1, p2 - точки, r - расстояние между ними
self.points = []
self.F = F
def append(self, *args, **kwargs):
self.points.append(Point(*args, **kwargs))
Теперь самое интересное — объявить функцию, которая возвращает «напряженность» в этой точке. Хотя это понятие относится к электромагнитному взаимодействию, в нашем случае это некоторый абстрактный вектор, вдоль которого мы и будем двигать точку. При этом у нас будет свойство точки q, в частном случае — заряд точки (в общем — что захотим, даже вектор). Итак, что такое напряженность в точке C? Что-то типа этого:
То есть напряженность в точке
class InteractionField:
...
def intensity(self, coord):
proj = Vector(*[0 for i in range(coord.dim())])
single_point = Point(Vector(), mass=1.0, q=1.0) # А вот и наша единичная точка (у нее нет координат, так как расстояние уже передается в F, а значит они нам не нужны)
for p in self.points:
if coord % p.coords < 10 ** (-10): # Этот по праву костыль здесь нужен, чтобы если вдруг мы спрашиваем про координаты точки, которая принадлежит полю, мы ее не учитывали (иначе напряженность неопределена)
continue
d = p.coords % coord
fmod = self.F(single_point, p, d) * (-1) # Тут мы получаем -модуль силы
proj = proj + (coord - p.coords) / d * fmod # суммируем
return proj
На этом моменте уже можно нарисовать векторное поле, но мы будем делать это в конце. Теперь сделаем шаг нашего взаимодействия
class InteractionField:
...
def step(self, dt):
self.clean_acc()
for p in self.points:
p.accinc(self.intensity(p.coords) * p.q)
p.accelerate(dt)
p.move(dt)
Тут все просто. Для каждой точки мы определяем напряженность в этих координатах а затем определяем конечную силу на ЭТУ материальную точку:
Определим недостающие функции.
Весь код InteractionField
class InteractionField:
def __init__(self, F):
self.points = []
self.F = F
def move_all(self, dt):
for p in self.points:
p.move(dt)
def intensity(self, coord):
proj = Vector(*[0 for i in range(coord.dim())])
single_point = Point(Vector(), mass=1.0, q=1.0)
for p in self.points:
if coord % p.coords < 10 ** (-10):
continue
d = p.coords % coord
fmod = self.F(single_point, p, d) * (-1)
proj = proj + (coord - p.coords) / d * fmod
return proj
def step(self, dt):
self.clean_acc()
for p in self.points:
p.accinc(self.intensity(p.coords) * p.q)
p.accelerate(dt)
p.move(dt)
def clean_acc(self):
for p in self.points:
p.clean_acc()
def append(self, *args, **kwargs):
self.points.append(Point(*args, **kwargs))
def gather_coords(self):
return [p.coords for p in self.points]
Частный случай. Перемещение частиц и визуализация векторного поля
Вот мы и дошли до самого интересного. Начнем с…
Моделирование движения частиц в электромагнитном поле
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
for i in range(3):
u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)
Вообще-то коэффициент k должен быть равен каким-то там миллиардам (9*10^(-9)), но так как он же будет гаситься временем t -> 0, я сразу решил сделать и то и другое адекватными числами. Поэтому в нашей физике k=300'000. А со всем остальным, думаю, понятно.
r ** 2 + 0.1
— это избежание деления на 0. Мы, конечно, могли бы заморочиться, решить большующую систему диффуров, но во-первых нет уравнения движения для более чем 2 тел, а во-вторых это явно уже не входит в понятие «статья для новичков»
— это избежание деления на 0. Мы, конечно, могли бы заморочиться, решить большующую систему диффуров, но во-первых нет уравнения движения для более чем 2 тел, а во-вторых это явно уже не входит в понятие «статья для новичков»
Далее мы добавляем десять точек (2-мерного пространства) с координатами от 0 до 10 по каждой из осей. Также, мы даем каждой точке заряд от -0.25 до 0.25. Теперь сделаем цикл и нарисуем точки по их координата (и следы):
X, Y = [], []
for i in range(130):
u.step(0.0006)
xd, yd = zip(*u.gather_coords())
X.extend(xd)
Y.extend(yd)
plt.figure(figsize=[8, 8])
plt.scatter(X, Y)
plt.scatter(*zip(*u.gather_coords()), color="orange")
plt.show()
Что должно было получиться:
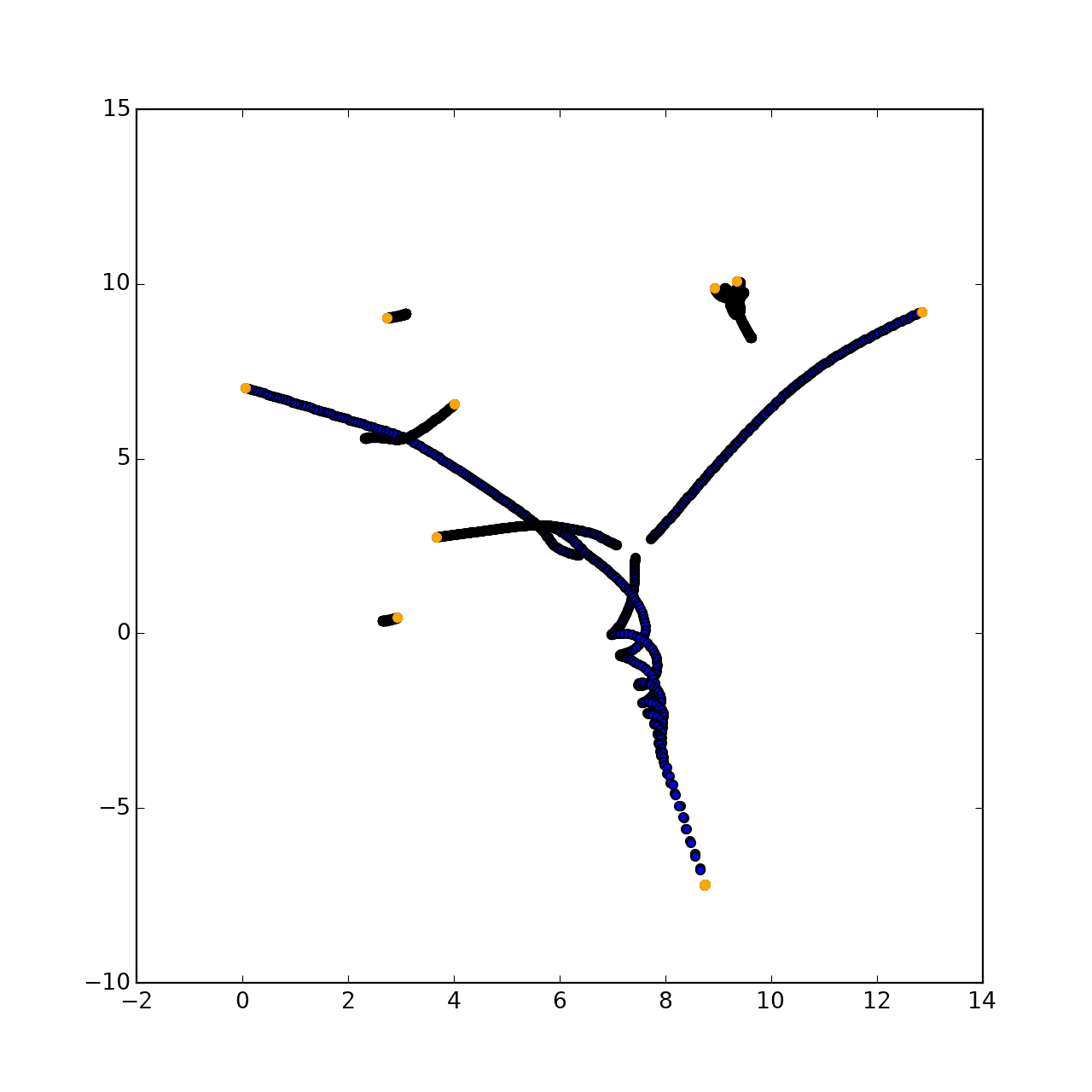
На самом деле рисунок там будет совершенно рандомный, ведь траектория каждой точки непредсказуема на данный момент развития механики.
Визуализация векторного поля
Тут все просто. Нам нужно пройтись по координатам с каким-то шагом и нарисовать в каждых из них вектор в нужном направлении.
fig = plt.figure(figsize=[5, 5])
res = []
STEP = 0.3
for x in np.arange(0, 10, STEP):
for y in np.arange(0, 10, STEP):
inten = u.intensity(Vector(x, y))
F = inten.mod()
inten /= inten.mod() * 4 # длина нашей палочки фиксирована
res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F))
for r in res:
plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) # Цвет по хитрой формуле чтобы добиться градиента
plt.show()
Примерно такой вывод должен был получиться.
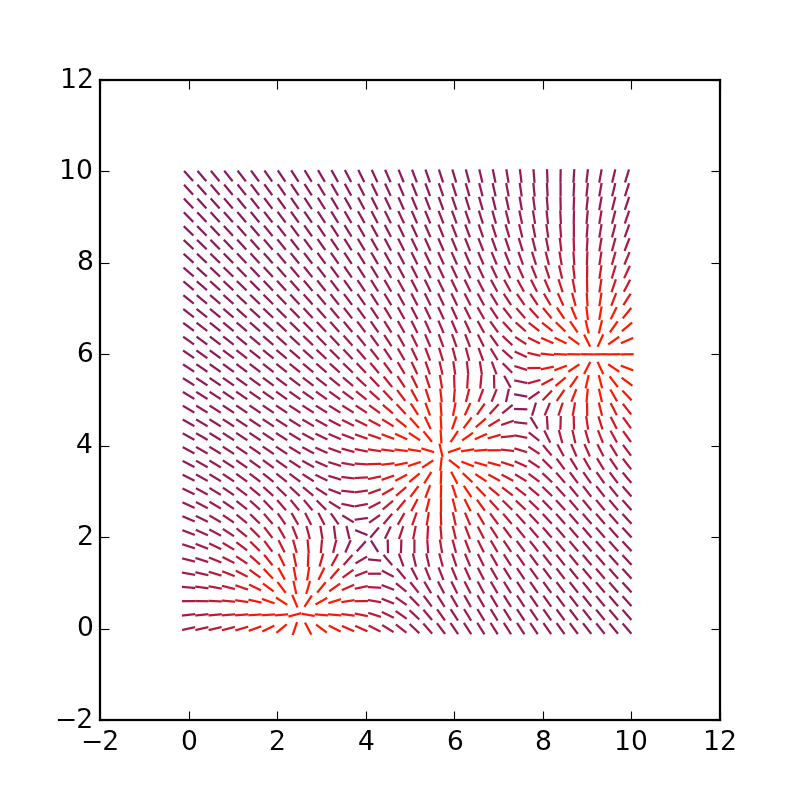
Можно удлинить сами векторы, заменим * 4 на * 1.5:
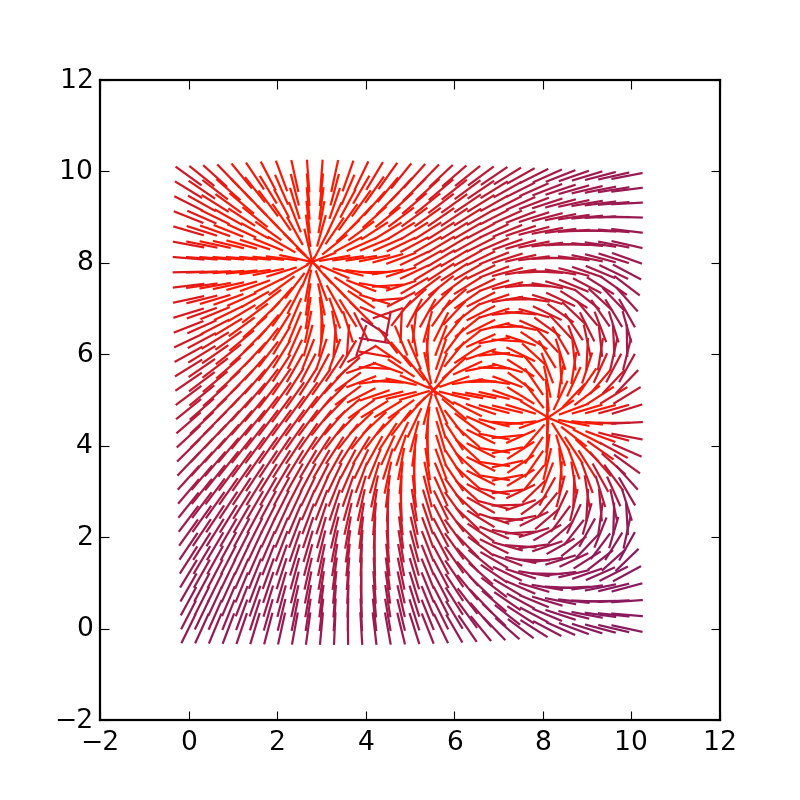
Играем с мерностью и моделированием
Создадим пятимерное пространство с 200 точек и взаимодействием, зависимым не от квадрата расстояния, а от 4-ой степени.
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1))
for i in range(200):
u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)
Теперь все координаты, скорости и т. д. определены в пяти измерениях. Теперь что-нибудь помоделируем:
velmod = 0
velocities = []
for i in range(100):
u.step(0.0005)
velmod = sum([p.speed.mod() for p in u.points]) # Добавляем сумму модулей скоростей всех точек
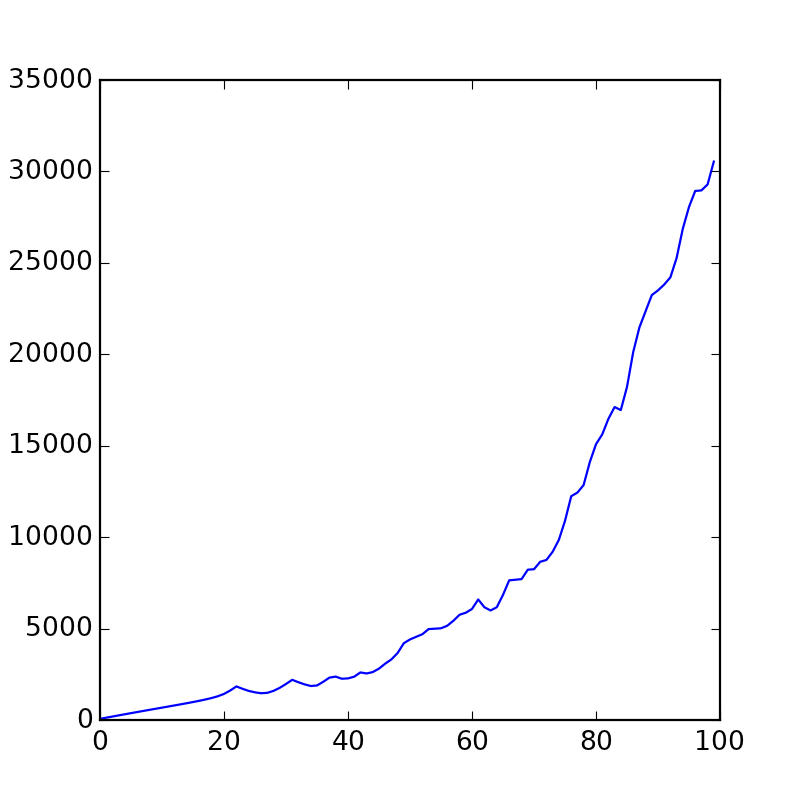
velocities.append(velmod)
plt.plot(velocities)
plt.show()
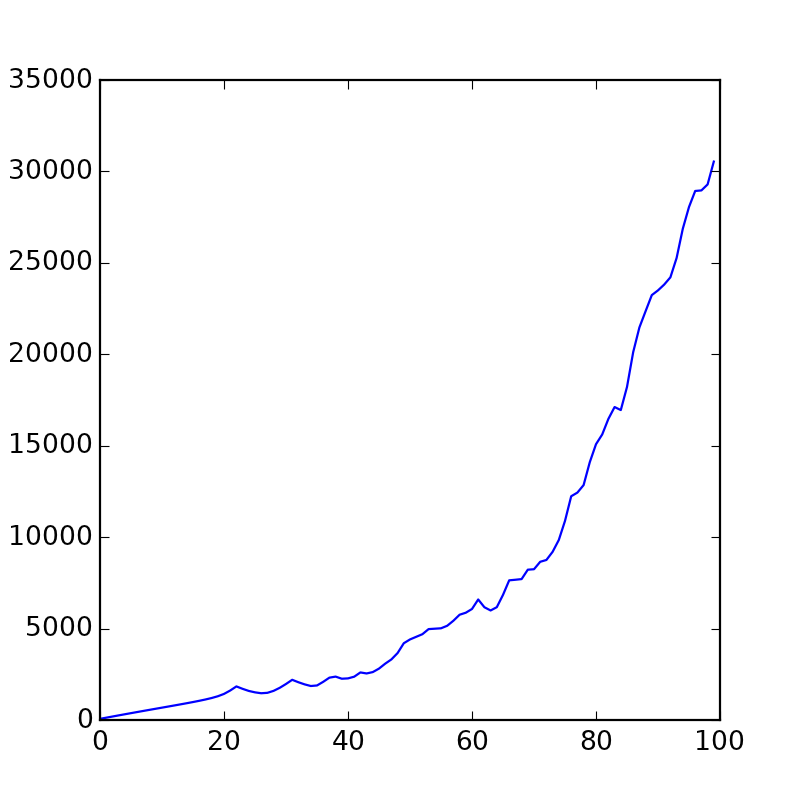
Это — график суммы всех скоростей в каждый момент времени. Как видите, со временем они потихоньку ускоряются.
Ну вот это была коротенькая инструкция как сделать такую простую штуку. А вот что бывает, если поиграться с цветами:
Весь код с демо
import random
class Vector(list):
def __init__(self, *el):
for e in el:
self.append(e)
def __add__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] + other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self + other
def __sub__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] - other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self - other
def __mul__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] * other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self * other
def __truediv__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] / other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self / other
def __pow__(self, other):
if type(other) is Vector:
assert len(self) == len(other), "Error 0"
r = Vector()
for i in range(len(self)):
r.append(self[i] ** other[i])
return r
else:
other = Vector.emptyvec(lens=len(self), n=other)
return self ** other
def __mod__(self, other):
return sum((self - other) ** 2) ** 0.5
def mod(self):
return self % Vector.emptyvec(len(self))
def dim(self):
return len(self)
def __str__(self):
if len(self) == 0:
return "Empty"
r = [str(i) for i in self]
return "< " + " ".join(r) + " >"
def _ipython_display_(self):
print(str(self))
@staticmethod
def emptyvec(lens=2, n=0):
return Vector(*[n for i in range(lens)])
@staticmethod
def randvec(dim):
return Vector(*[random.random() for i in range(dim)])
class Point:
def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties):
self.coords = coords
if speed is None:
self.speed = Vector(*[0 for i in range(len(coords))])
else:
self.speed = speed
self.acc = Vector(*[0 for i in range(len(coords))])
self.mass = mass
self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
self.q = q
for prop in properties:
setattr(self, prop, properties[prop])
def move(self, dt):
self.coords = self.coords + self.speed * dt
def accelerate(self, dt):
self.speed = self.speed + self.acc * dt
def accinc(self, force):
self.acc = self.acc + force / self.mass
def clean_acc(self):
self.acc = self.acc * 0
def __str__(self):
r = ["Point {"]
for p in self.__params__:
r.append(" " + p + " = " + str(getattr(self, p)))
r += ["}"]
return "\n".join(r)
def _ipython_display_(self):
print(str(self))
class InteractionField:
def __init__(self, F):
self.points = []
self.F = F
def move_all(self, dt):
for p in self.points:
p.move(dt)
def intensity(self, coord):
proj = Vector(*[0 for i in range(coord.dim())])
single_point = Point(Vector(), mass=1.0, q=1.0)
for p in self.points:
if coord % p.coords < 10 ** (-10):
continue
d = p.coords % coord
fmod = self.F(single_point, p, d) * (-1)
proj = proj + (coord - p.coords) / d * fmod
return proj
def step(self, dt):
self.clean_acc()
for p in self.points:
p.accinc(self.intensity(p.coords) * p.q)
p.accelerate(dt)
p.move(dt)
def clean_acc(self):
for p in self.points:
p.clean_acc()
def append(self, *args, **kwargs):
self.points.append(Point(*args, **kwargs))
def gather_coords(self):
return [p.coords for p in self.points]
# ДЕМО
import matplotlib.pyplot as plt
import numpy as np
import time
# Моделирование частиц со следами
if False:
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
for i in range(10):
u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2)
X, Y = [], []
for i in range(130):
u.step(0.0006)
xd, yd = zip(*u.gather_coords())
X.extend(xd)
Y.extend(yd)
plt.figure(figsize=[8, 8])
plt.scatter(X, Y)
plt.scatter(*zip(*u.gather_coords()), color="orange")
plt.show()
def sigm(x):
return 1 / (1 + 1.10 ** (-x/1000))
# Визуализация векторного поля
if False:
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
for i in range(3):
u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)
fig = plt.figure(figsize=[5, 5])
res = []
STEP = 0.3
for x in np.arange(0, 10, STEP):
for y in np.arange(0, 10, STEP):
inten = u.intensity(Vector(x, y))
F = inten.mod()
inten /= inten.mod() * 1.5
res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F))
for r in res:
plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2]))))
plt.show()
# Подсчет скоростей в 5-мерном пространстве
if False:
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1))
for i in range(200):
u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)
velmod = 0
velocities = []
for i in range(100):
u.step(0.0005)
velmod = sum([p.speed.mod() for p in u.points])
velocities.append(velmod)
plt.plot(velocities)
plt.show()
Следующая статья будет возможно о более сложном моделировании, а быть может и флюидах и уравнениях Навье-Стокса.
UPD: Статья написана моим коллегой тут
Спасибо MomoDev за помощь в рендеринге видео.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Делать красоту на основе движения жидкости?
100% Да64
0% Не очень0
Проголосовали 64 пользователя. Воздержались 7 пользователей.







