При расчёте срока проекта традиционно мы оцениваем длительность промежуточных шагов, затем их суммируем и прибавляем буфер на всякие случайности. Затем руководство режет нам этот срок вдвое. В рамках данной заметки автора будут интересовать наши расчёты, потому что даже руководитель проектов с большим опытом зачастую понимает, что рассчитанный срок слишком короткий и сильно, иногда в разы, расходится с его личной экспертной оценкой. Да, он поправит оценки сроков проекта и промежуточных шагов до своей экспертной оценки и при истинном мастерстве с некоторыми переработками уложится в срок с точностью до 15%, но осадочек останется.
Данная заметка объясняет причину расхождения экспертной и теоретически рассчитанной оценок. Также рассмотрено, почему “завышенная” экспертная оценка обычно оказывается занижена, если она не делается на основе статистических данных по выполнению аналогичных проектов. Под конец раскрыто как корректно посчитать срок проекта и объяснить ситуацию заинтересованным лицам до начала проекта или в ходе проекта.
Когда мы оцениваем срок реализации кусочка работы, мы определяем наиболее вероятную цифру. Это может быть экспертная оценка по одной точке или по трём точкам, как в PERT. В сложном проекте это может быть параметрическое моделирование. Во всех вариантах мы совершаем одну и ту же ошибку. Дело в том, что во всех классических методах оценки предполагается, что у нас нормальное распределение оцениваемой величины — по Гауссу. Теоретики очень любят это распределение.
Нормальное распределение означает, что проект с корректно оценённой длительностью 6 месяцев с равной вероятностью завершится через 9 месяцев или через 3 месяца. На равных расстояниях от центра распределения вероятность завершения проекта равна — такова особенность кривой Гаусса. С другой стороны, на практике мало кто видел IT-проект, завершившийся в два раза быстрее (через 3 месяца), зато проекты затянувшиеся в полтора раза по срокам (9 месяцев) мы видим регулярно. Кроме того, при нормальном распределении половина проектов у нас заканчивалась бы до оценённого срока, а половина — после. Но этого на практике тоже не наблюдается. Это говорит о том, что нормальное распределение для оценки сроков неприменимо. То есть у нас не нормальное распределение, а какое-то иное, с разной вероятностью завершения до наиболее вероятного срока и после.
Рассмотрим в качестве примера подобного распределения логнормальное. Оно нам покажет особенности данного класса распределений. Для логнормального распределения медиана и математическое ожидание находятся существенно дальше пика:
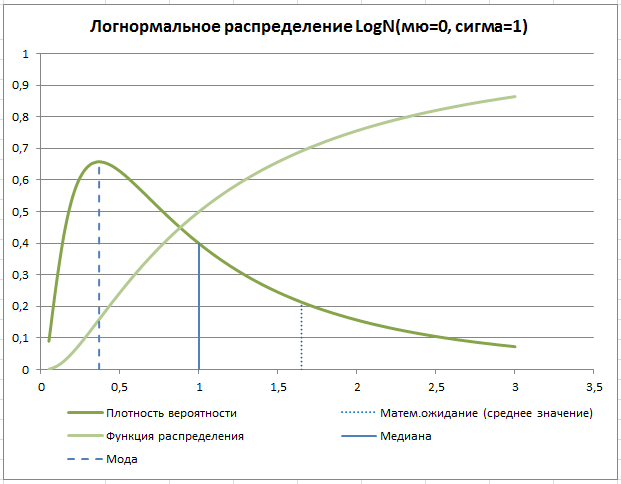
На представленном графике пик показывает наибольшую вероятность срока завершения проекта В план проекта обычно вписывается эта цифра плюс некий запас. Медиана указывает на точку разделения при которой половина проектов завершится до этого срока, а вторая половина — после. Математическое ожидание указывает среднее значение длительности проекта. Для фрагмента работы распределение будет иметь те же самые особенности: большую разницу между наиболее ожидаемым сроком реализации фрагмента работы (на основе него традиционно строятся планы) и средним значением срока.
Чтобы спрогнозировать длительность проекта, мы определяем самую длинную по времени цепочку и складываем длительности её фрагментов. Если мы складываем так величины, распределённые по Гауссу, то в среднем должен получиться корректный итоговый срок. Ведь половина фрагментов работы завершиться раньше срока, половина позже и эти неоднородности взаимно скомпенсируются. Чем больше фрагментов, тем точнее скомпенсируются неоднородности. Плюс мы можем посчитать погрешность и чуть сдвинуть срок на сигму-другую в зависимости от последствий срыва сроков.
Но у нас не распределение Гаусса. У нас удлинение срока выполнения каждого фрагмента работы значительно вероятнее, чем укорачивание на такую же величину. В итоге, если мы складываем сроки наиболее вероятного завершения каждого фрагмента работы, то у нас неоднородности по срокам выполнения не компенсируются, а усиливаются. Причём усиливаются в сторону удлинения реального среднего срока проекта по сравнению с оценкой. Что мы и наблюдаем в реальной жизни: если первый срок просрочен, то будут просрочены и все остальные сроки, при этом просрочка будет только расти. Лишь прикладывая дополнительные усилия можно остановить рост отставания проекта.
Особенностью данного способа подсчёта является известный факт: чем мельче дробить работы для оценки срока проекта, тем менее точной оказывается оценка. Хотя по теории должно быть ровно наоборот. Причина этого в том, что наша экспертная оценка для всей работы и для составляющих её частей берётся из опыта. Опыт оценивает каждый элемент независимо, а не исходя из арифметики, согласно которой длительность работы должна быть суммой длительностей составляющих её частей. Арифметика здесь не работает, так как сумма наиболее вероятных сроков завершения частей не даёт наиболее вероятный срок завершения всей работы — корректно суммировать можно только математические ожидания.
Если мы пытаемся чуть сдвинуть оценённый срок для всего проекта или его частей на сигму-другую, считая распределение нормальным, то это не сильно помогает, так как хвост распределения сильно толще, чем у кривой Гаусса. В итоге, за счёт такого увеличения оценки срока не удаётся дойти даже до медианы, не говоря уже о среднем значении длительности проекта в виде математического ожидания.
С одной стороны, складывать следует математические ожидания. С другой стороны, мы не математики. Мы из реальной жизни и понимаем проблемность расчёта параметров графиков даже когда на это есть время и какая-то накопленная статистика. Но есть другие пути. В конце-концов, проблеме оценки сроков не один десяток лет и с этим практики работать научились.
Метод Брукса: считаем срок реализации программы “в лоб” (пользователем выступает сам программист) и умножаем на 3 для программного продукта (пользователем выступает неограниченный круг лиц) или программного комплекса (в текущих реалиях — набор микросервисов) и на 9 для системного программного продукта (в текущих реалиях — набор связанных инфраструктурных компонентов). Откуда берутся такие коэффициенты хорошо теоретически обосновано в первой главе книги Брукса “Мифический человеко-месяц” и это описание 1975 года хорошо перекладывается на текущие реалии.
Метод Скрама: вводим абстрактную промежуточную единицу трудоёмкости реализации функционала, смотрим статистику реализации командой измеренного в данных единицах функционала, просим команду оценить трудоёмкость задач проекта, переводим единицы в Скрам-итерации (спринты) известной длины и получаем оценку сроков для данной команды разработки. Так как мы работаем с реально собранной статистикой и команда отвечает за свои оценки по трудоёмкости, то привязка длительности к единице трудоёмкости является математическим ожиданием и поэтому половина спринтов будет заканчиваться чуть раньше, половина чуть позже. На практике в половине итераций Скрама придётся у команды забрать часть задач, а в половине добавить незапланированных, чтобы длина спринта оставалась постоянной.
Задача переноса Скрам-оценки одной команды на другую команду является искусством. Они не переносятся простым введением коэффициента перевода единиц трудоёмкости одной команды в единицы трудоёмкости другой команды. Дело в том, что одна команда имеет в своём составе хорошего фронтендера, но в ней нет хорошего специалиста по базе, а другая команда имеет хорошего специалиста по базе, но фронтовые задачи для неё повышенной сложности. Отличия в специализации разработчиков приведут к тому, что относительно бэкендовых задач у одной команды будет перегиб по сложности в сторону задач по базе данных, а у другой — по фронту. Кроме того, команда сама определяет необходимый уровень внутреннего качества продукта и разные команды определяют его несколько иначе, чем соседние команды, что также затрудняет пересчёт единиц трудоёмкости. То есть можно перевести промежуточные единицы одной команды в промежуточные единицы другой команды сравнивая оценки схожих задач, но эти задачи должны браться из разных типов деятельности, с учётом сильных и слабых сторон команд и с учётом особенностей настройки их Скрамов.
Метод функциональных элементов: вводим промежуточную единицу трудоёмкости, составляем список функциональных элементов (экраны в браузере, микросервисы, настраиваемые элементы инфраструктуры и т.д.), оцениваем трудоёмкость работы над каждым функциональным элементом в промежуточных единицах. После этого по своему экспертному опыту работы с конкретной командой разработчиков оцениваем переводной коэффициент промежуточной единицы во время. Лично я ещё независимо оцениваю переводные коэффициенты для разных видов деятельности: аналитики, проектирования, написания постановок задач, написания кода, вёрстки, тестирования, интеграции и т.д. После этого следует учесть порядок операций, характерное время задержки между завершением предыдущей операции и началом новой и определить длительность проекта методом критического пути.
До сих пор мы работали с внутренними факторами проекта. Но у нас есть и внешние: внешние подрядчики, смежные подразделения, поставщики и клиент. Проблемы с ними ровно те же самые: они в два раза быстрее делают или отвечают сильно реже, чем в полтора раза дольше наиболее вероятного значения. То есть там тоже нет нормального распределения по срокам. Это тоже следует закладывать и учитывать на основе статистики работы с клиентами, подрядчиками и смежными подразделениями и, по возможности, защищаться с помощью штрафных санкций.
И вот, мы оценили прогнозную длительность проекта. Как обосновать полученный срок? На основе проделанных расчётов. Например, автор заметки для не-Скрам проектов обычно делает в Google Sheets большую многострочную наглядную таблицу с детальным расчётом методом функциональных элементов. Расчёт опирается на практику, все коэффициенты и параметры наглядны, а практика для заинтересованных лиц обычно является сильным и хорошим аргументом, даже если получился неудобный для тех или иных лиц срок. Особенно практика наглядная и полученная в рамках текущей компании.
Согласятся ли заинтересованные лица, например руководство, с хорошо проделанной и донесённой оценкой по срокам? Далеко не всегда даже если заинтересованные лица полностью понимают и осознают, что оценка корректная. Иногда оценка неприемлема по внешним причинам, но это уже боль заинтересованных лиц, выливающаяся в трудном решении руководства по срокам. И тем не менее, видя опирающиеся на опыт расчёты, руководство и иные заинтересованные лица имеют возможность предсказуемо повлиять на итоговый срок проекта выделением дополнительных ресурсов и полномочий. Иногда понявшее ситуацию со сроками руководство будет продолжать резать сроки без выделения дополнительных ресурсов и полномочий. Как с этим жить — тема отдельной заметки.
Данная заметка объясняет причину расхождения экспертной и теоретически рассчитанной оценок. Также рассмотрено, почему “завышенная” экспертная оценка обычно оказывается занижена, если она не делается на основе статистических данных по выполнению аналогичных проектов. Под конец раскрыто как корректно посчитать срок проекта и объяснить ситуацию заинтересованным лицам до начала проекта или в ходе проекта.
Корень ошибки
Когда мы оцениваем срок реализации кусочка работы, мы определяем наиболее вероятную цифру. Это может быть экспертная оценка по одной точке или по трём точкам, как в PERT. В сложном проекте это может быть параметрическое моделирование. Во всех вариантах мы совершаем одну и ту же ошибку. Дело в том, что во всех классических методах оценки предполагается, что у нас нормальное распределение оцениваемой величины — по Гауссу. Теоретики очень любят это распределение.
Нормальное распределение означает, что проект с корректно оценённой длительностью 6 месяцев с равной вероятностью завершится через 9 месяцев или через 3 месяца. На равных расстояниях от центра распределения вероятность завершения проекта равна — такова особенность кривой Гаусса. С другой стороны, на практике мало кто видел IT-проект, завершившийся в два раза быстрее (через 3 месяца), зато проекты затянувшиеся в полтора раза по срокам (9 месяцев) мы видим регулярно. Кроме того, при нормальном распределении половина проектов у нас заканчивалась бы до оценённого срока, а половина — после. Но этого на практике тоже не наблюдается. Это говорит о том, что нормальное распределение для оценки сроков неприменимо. То есть у нас не нормальное распределение, а какое-то иное, с разной вероятностью завершения до наиболее вероятного срока и после.
Рассмотрим в качестве примера подобного распределения логнормальное. Оно нам покажет особенности данного класса распределений. Для логнормального распределения медиана и математическое ожидание находятся существенно дальше пика:

На представленном графике пик показывает наибольшую вероятность срока завершения проекта В план проекта обычно вписывается эта цифра плюс некий запас. Медиана указывает на точку разделения при которой половина проектов завершится до этого срока, а вторая половина — после. Математическое ожидание указывает среднее значение длительности проекта. Для фрагмента работы распределение будет иметь те же самые особенности: большую разницу между наиболее ожидаемым сроком реализации фрагмента работы (на основе него традиционно строятся планы) и средним значением срока.
Чтобы спрогнозировать длительность проекта, мы определяем самую длинную по времени цепочку и складываем длительности её фрагментов. Если мы складываем так величины, распределённые по Гауссу, то в среднем должен получиться корректный итоговый срок. Ведь половина фрагментов работы завершиться раньше срока, половина позже и эти неоднородности взаимно скомпенсируются. Чем больше фрагментов, тем точнее скомпенсируются неоднородности. Плюс мы можем посчитать погрешность и чуть сдвинуть срок на сигму-другую в зависимости от последствий срыва сроков.
Но у нас не распределение Гаусса. У нас удлинение срока выполнения каждого фрагмента работы значительно вероятнее, чем укорачивание на такую же величину. В итоге, если мы складываем сроки наиболее вероятного завершения каждого фрагмента работы, то у нас неоднородности по срокам выполнения не компенсируются, а усиливаются. Причём усиливаются в сторону удлинения реального среднего срока проекта по сравнению с оценкой. Что мы и наблюдаем в реальной жизни: если первый срок просрочен, то будут просрочены и все остальные сроки, при этом просрочка будет только расти. Лишь прикладывая дополнительные усилия можно остановить рост отставания проекта.
Особенностью данного способа подсчёта является известный факт: чем мельче дробить работы для оценки срока проекта, тем менее точной оказывается оценка. Хотя по теории должно быть ровно наоборот. Причина этого в том, что наша экспертная оценка для всей работы и для составляющих её частей берётся из опыта. Опыт оценивает каждый элемент независимо, а не исходя из арифметики, согласно которой длительность работы должна быть суммой длительностей составляющих её частей. Арифметика здесь не работает, так как сумма наиболее вероятных сроков завершения частей не даёт наиболее вероятный срок завершения всей работы — корректно суммировать можно только математические ожидания.
Если мы пытаемся чуть сдвинуть оценённый срок для всего проекта или его частей на сигму-другую, считая распределение нормальным, то это не сильно помогает, так как хвост распределения сильно толще, чем у кривой Гаусса. В итоге, за счёт такого увеличения оценки срока не удаётся дойти даже до медианы, не говоря уже о среднем значении длительности проекта в виде математического ожидания.
Что делать
С одной стороны, складывать следует математические ожидания. С другой стороны, мы не математики. Мы из реальной жизни и понимаем проблемность расчёта параметров графиков даже когда на это есть время и какая-то накопленная статистика. Но есть другие пути. В конце-концов, проблеме оценки сроков не один десяток лет и с этим практики работать научились.
Метод Брукса: считаем срок реализации программы “в лоб” (пользователем выступает сам программист) и умножаем на 3 для программного продукта (пользователем выступает неограниченный круг лиц) или программного комплекса (в текущих реалиях — набор микросервисов) и на 9 для системного программного продукта (в текущих реалиях — набор связанных инфраструктурных компонентов). Откуда берутся такие коэффициенты хорошо теоретически обосновано в первой главе книги Брукса “Мифический человеко-месяц” и это описание 1975 года хорошо перекладывается на текущие реалии.
Метод Скрама: вводим абстрактную промежуточную единицу трудоёмкости реализации функционала, смотрим статистику реализации командой измеренного в данных единицах функционала, просим команду оценить трудоёмкость задач проекта, переводим единицы в Скрам-итерации (спринты) известной длины и получаем оценку сроков для данной команды разработки. Так как мы работаем с реально собранной статистикой и команда отвечает за свои оценки по трудоёмкости, то привязка длительности к единице трудоёмкости является математическим ожиданием и поэтому половина спринтов будет заканчиваться чуть раньше, половина чуть позже. На практике в половине итераций Скрама придётся у команды забрать часть задач, а в половине добавить незапланированных, чтобы длина спринта оставалась постоянной.
Задача переноса Скрам-оценки одной команды на другую команду является искусством. Они не переносятся простым введением коэффициента перевода единиц трудоёмкости одной команды в единицы трудоёмкости другой команды. Дело в том, что одна команда имеет в своём составе хорошего фронтендера, но в ней нет хорошего специалиста по базе, а другая команда имеет хорошего специалиста по базе, но фронтовые задачи для неё повышенной сложности. Отличия в специализации разработчиков приведут к тому, что относительно бэкендовых задач у одной команды будет перегиб по сложности в сторону задач по базе данных, а у другой — по фронту. Кроме того, команда сама определяет необходимый уровень внутреннего качества продукта и разные команды определяют его несколько иначе, чем соседние команды, что также затрудняет пересчёт единиц трудоёмкости. То есть можно перевести промежуточные единицы одной команды в промежуточные единицы другой команды сравнивая оценки схожих задач, но эти задачи должны браться из разных типов деятельности, с учётом сильных и слабых сторон команд и с учётом особенностей настройки их Скрамов.
Метод функциональных элементов: вводим промежуточную единицу трудоёмкости, составляем список функциональных элементов (экраны в браузере, микросервисы, настраиваемые элементы инфраструктуры и т.д.), оцениваем трудоёмкость работы над каждым функциональным элементом в промежуточных единицах. После этого по своему экспертному опыту работы с конкретной командой разработчиков оцениваем переводной коэффициент промежуточной единицы во время. Лично я ещё независимо оцениваю переводные коэффициенты для разных видов деятельности: аналитики, проектирования, написания постановок задач, написания кода, вёрстки, тестирования, интеграции и т.д. После этого следует учесть порядок операций, характерное время задержки между завершением предыдущей операции и началом новой и определить длительность проекта методом критического пути.
До сих пор мы работали с внутренними факторами проекта. Но у нас есть и внешние: внешние подрядчики, смежные подразделения, поставщики и клиент. Проблемы с ними ровно те же самые: они в два раза быстрее делают или отвечают сильно реже, чем в полтора раза дольше наиболее вероятного значения. То есть там тоже нет нормального распределения по срокам. Это тоже следует закладывать и учитывать на основе статистики работы с клиентами, подрядчиками и смежными подразделениями и, по возможности, защищаться с помощью штрафных санкций.
Обоснование сроков
И вот, мы оценили прогнозную длительность проекта. Как обосновать полученный срок? На основе проделанных расчётов. Например, автор заметки для не-Скрам проектов обычно делает в Google Sheets большую многострочную наглядную таблицу с детальным расчётом методом функциональных элементов. Расчёт опирается на практику, все коэффициенты и параметры наглядны, а практика для заинтересованных лиц обычно является сильным и хорошим аргументом, даже если получился неудобный для тех или иных лиц срок. Особенно практика наглядная и полученная в рамках текущей компании.
Согласятся ли заинтересованные лица, например руководство, с хорошо проделанной и донесённой оценкой по срокам? Далеко не всегда даже если заинтересованные лица полностью понимают и осознают, что оценка корректная. Иногда оценка неприемлема по внешним причинам, но это уже боль заинтересованных лиц, выливающаяся в трудном решении руководства по срокам. И тем не менее, видя опирающиеся на опыт расчёты, руководство и иные заинтересованные лица имеют возможность предсказуемо повлиять на итоговый срок проекта выделением дополнительных ресурсов и полномочий. Иногда понявшее ситуацию со сроками руководство будет продолжать резать сроки без выделения дополнительных ресурсов и полномочий. Как с этим жить — тема отдельной заметки.
