Цепи Маркова для процедурной генерации зданий

Примечание: полный исходный код этого проекта можно найти [здесь]. Так как он является частью более масштабного проекта, я рекомендую смотреть коммит на момент выпуска этой статьи, или файл /source/helpers/arraymath.h, а также /source/world/blueprint.cpp.

В этой статье я хочу подробно рассказать о принципах использования цепей Маркова и статистики для процедурной генерации 3D-зданий и других систем.

Я объясню математические основы работы системы и постараюсь сделать объяснение как можно более общим, чтобы вы могли применять эту концепцию в других ситуациях, например, для генерации 2D-подземелий. Объяснение будет сопровождаться изображениями и исходным кодом.

Этот метод является обобщённым способом процедурной генерации систем, удовлетворяющих определённым требованиям, поэтому я рекомендую дочитать хотя бы до конца первого раздела, чтобы вы могли понять, сможет ли эта методика быть полезной в вашем случае, потому что ниже я объясняю необходимые требования.

Результаты будут использоваться в моём воксельном движке, чтобы task-боты могли строить здания,, а затем города. В самом конце статьи есть пример!


Пара примеров с результатами.

Основы

Цепи Маркова

Цепи Маркова — это последовательность состояний, по которой движется система, описываемая переходами во времени. Переходы между состояниями стохастичны, то есть описываются вероятностями, которые являются характеристикой системы.

Система задаётся пространством состояний, которое является пространством всем возможных конфигураций системы. Если система описана верно, то мы также можем описать переходы между состояниями как дискретные шаги.

Надо учесть, что из одного состояния системы часто бывает несколько возможных дискретных переходов, каждый из которых ведёт к разному состоянию системы.

Вероятность перехода из состояния i в состояние j равна:

Марковский процесс — это процесс исследования этого пространства состояний при помощи передаваемых ему вероятностей.

Важно то, что марковские процессы «не имеют памяти». Это просто значит, что вероятности перехода из текущего состояния к новому зависят только от текущего состояния и больше ни от каких других состояний, посещённых ранее.

Пример: генерация текста

Система — это последовательность битов. Пространство состояний — это все возможные последовательности битов. Дискретный переход будет изменять один бит с 0 на 1 или 1 на 0. Если система имеет n битов, то из каждого состояния у нас есть n возможных переходов к новому состоянию. Марковский процесс будет заключаться в исследовании пространства состояний сменой значений битов в последовательности с использованием определённых вероятностей.

Пример: прогнозирование погоды

Система — это текущие погодные условия. Пространство состояний — это все возможные состояния, в которых может находиться погода (например, «дождливо», «облачно», «солнечно» и т.д.). Переходом будет переключение из любого состояния в другое состояние, в котором мы можем задать вероятность перехода (например, «какова вероятность того, что если сегодня солнечно, то завтра будет дождь, вне зависимости от вчерашней погоды?»).

Метод Монте-Карло для цепей Маркова

Так как переходы между состояниями определяются вероятностями, мы также можем задать вероятность «устойчивого» нахождения в любом состоянии (или, если время стремится к бесконечности, среднее время, которое мы будем находиться в конкретном состоянии). Это внутреннее распределение состояний.

Тогда алгоритм Монте-Карло для цепей Маркова (Markov-Chain Monte-Carlo, MCMC) — это методика получения выборки из пространства состояний. Выборка (сэмплирование) означает выбор состояния на основании вероятности выбора с учётом внутреннего распределения.

Говорят, что вероятность нахождения в состоянии пропорциональна* некой функции затрат, которая даёт «оценку» текущему состоянию, в котором находится система. Считается, что если затраты низки, то вероятность нахождения в этом состоянии высока, и это соотношение монотонно. Функция затрат задаётся следующим образом:

Примечание: я не уверен, правильно ли здесь использовать слово «пропорциональна», потому что соотношение не обязательно является линейным.

Тогда выборка из распределения состояний будет возвращать конфигурацию с низкими затратами (или хорошей «оценкой») с более высокой вероятностью!

Даже при чрезвычайно большом пространстве состояний (возможно бесконечном, но «счётно бесконечном»), вне зависимости от сложности системы алгоритм MCMC будет находить решение с низкими затратами, если мы дадим ему достаточно времени для схождения.

Подобное выполнение исследования пространства состояний является стандартной техникой стохастической оптимизации и имеет множество применений в таких областях, как машинное обучение.

Распределение Гиббса

Примечание: если этот раздел вам непонятен, можете спокойно его пропустить. Вы всё равно сможете воспользоваться реализацией системы.

После того, как мы определили затраты для возможного состояния, как нам определить вероятность этого состояния?

Решение: распределение Гиббса — это распределение максимальной энтропии при заданном множестве ограничений.

По сути, это значит, что если мы зададим множество ограничений для вероятностей системы, то распределение Гиббса создаст «наименьшее количество допущений» о форме распределения.

Примечание: распределение Гиббса также является распределением с наименьшей чувствительностью к вариациям в ограничениях (по метрике расхождения Кульбака-Лейблера).

Единственное ограничение, которое мы накладываем на распределение состояний — это функция затрат, поэтому мы используем её в распределении Гиббса для вычисления вероятности перехода между состояниями:

Где Z — это функция разбиения множества переходов из состояния i. Это нормирующий множитель, гарантирующий, что сумма вероятностей переходов из любого состояния равна 1.

Заметим, что если мы решим, что следующее состояние будет тем же состоянием, то относительные затраты равны нулю, то есть вероятность после нормализации будет ненулевой (из-за формы распределения с показателем)! Это значит, что во множество переходов нужно включить вероятность неизменения состояний.

Стоит также заметить, что распределение Гиббса параметризуется «вычислительной температурой» T.

Одно из ключевых преимуществ использования вероятностей при исследовании пространства состояний заключается в том, что система может выполнять переходы в более затратные состояния (поскольку они имеют ненулевую вероятность перехода), превращая алгоритм в «нежадный» метод оптимизации.

Заметим, что при стремлении температуры к бесконечности вероятность любого отдельного перехода стремится к единице таким образом, что при нормализации множества вероятностей всех переходов из состояния они становятся равновероятными (или распределение Гиббса приближается к нормальному распределению), несмотря на то, что их затраты больше!

При приближении вычислительной температуры к нулю более вероятными становятся переходы с меньшими затратами, то есть вероятность предпочтительных переходов повышается.

При выполнении исследования/оптимизации пространства состояний мы постепенно снижаем температуру. Этот процесс называется «имитацией отжига». Благодаря этому мы в начале можем легко выйти из локального минимума, а в конце выбирать наилучшие решения.

Когда температура достаточно мала, то все вероятности стремятся к нулю, за исключением вероятности отсутствия перехода!

Так происходит потому, что только отсутствие перехода имеет нулевую разность затрат, то есть нахождение в том же состоянии не зависит от температуры. Из-за формы показательной функции при T = 0 это оказывается единственная вероятность с ненулевым значением, то есть после нормализации она превращается в единицу. Следовательно, наша система сойдётся к устойчивой точке и дальнейшее охлаждение больше не будет нужно. Это неотъемлемое свойство генерации вероятностей при помощи распределения Гиббса.

Процесс схождения системы можно настраивать при помощи изменения скорости остывания!

Если охлаждение происходит медленнее, то в результате мы обычно приходим к решению с меньшими затратами (в определённой степени), но ценой большего количества шагов сходимости. Если охлаждение происходит быстрее, то выше вероятность того, что система на ранних этапах попадёт в ловушку подобласти с бОльшими затратами, то есть мы получим «менее оптимальные» результаты.

Следовательно, марковский процесс не просто генерирует случайные результаты, а пытается сгенерировать «хорошие» результаты и с высокой вероятностью ему это удастся!

По определению произвольных функций затрат уникальный оптимум не обязан существовать. Этот метод вероятностной оптимизации генерирует только приближении к оптимуму, пытаясь минимизировать функцию затрат, и из-за выполнения выборки каждый раз будет генерировать разные результаты (если генератор случайных чисел имеет различный seed).

Сам процесс выборки может выполняться при помощи метода обратного преобразования над функцией распределения масс нашего дискретного множества переходов. Позже я покажу, как это делается.

Процедурная генерация

Чем этот метод полезен для процедурной генерации?

В некоторых системах часто бывает сложно определить простой алгоритм, генерирующий хорошие результаты, особенно в случае сложных систем.

Задание произвольных правил генерации не только сложно, но и ограничено только нашим воображением и обработкой граничных случаев.

Если система удовлетворяет определённому набору требований, то применение MCMC позволяет нам не волноваться о подборе алгоритма или правил. Вместо этого мы определяем метод для генерации любого возможного результата, и осознанно выбираем хороший на основании его «оценки».

Предъявляются следующие требования:

• Система может находиться в дискретной (возможно бесконечной) конфигурации состояний.
• Мы можем задавать дискретные переходы между состояниями.
• Мы можем задать функцию затрат, оценивающую текущее состояние системы.

Ниже я приведу некоторые другие примеры, в которых по моему мнению можно применить этот метод.

Реализация

Псевдокод

В своей реализации мы хотим добиться следующего:

• Задать состояние системы.
• Задать все возможные переходы к следующему состоянию.
• Вычислить затраты текущего состояния.
• Вычислить затраты всех возможных следующих состояний (или их подмножества).
• Вычислить при помощи распределения Гиббса вероятность переходов.
• Выполнить выборку (сэмплировать) переходы при помощи вероятностей.
• Выполнить сэмплированный переход.
• Снизить вычислительную температуру.
• Повторять шаги, пока не получим удовлетворительных результатов.

В виде псевдокода алгоритм MCMC выглядит следующим образом:

//Алгоритм MCMC для сэмплирования состояния

T = 200; //Некое исходное значение вычислительной температуры
State s = initialState();
Transitions t[n] = {...} //n возможных переходов
thresh = 0.01; //Критерий сходимости (по температуре)

//Выполняем итерации, пока не достигнем критерия сходимости
while(T > thresh){

  //Вычисляем текущие затраты состояния
  curcost = costfunc(s);
  newcost[n] = {0};     //Инициализируем newcost со значением 0
  probability[n] = {0}; //Инициализируем вероятность перехода со значением 0

  //Вычисляем вероятности
  for(i = 0; i < n; i++){
    newcost[i] = costfunc(doTransition(s, t[i]));
    probability[i] = exp(-(newcost[i] - curcost)/T);
  }

  //Нормализуем вероятности
  probability /= sum(probability);

  //Сэмплируем переход
  sampled = sample_transition(t, probability);

  //Выполняем переход
  s = doTransition(s, sampled);

  //Снижаем температуру
  T *= 0.975;
}

Генерация 3D-зданий

Пространство состояний и переходы

Для генерации зданий в 3D я генерирую множество комнат с объёмом, заданным ограничивающим параллелепипедом.

struct Volume{
  //Углы ограничивающего параллелепипеда
  glm::vec3 a;
  glm::vec3 b;

  void translate(glm::vec3 shift);
  int getVol();
};

//Получаем общий объём
int Volume::getVol(){
  return abs((b.x-a.x)*(b.y-a.y)*(b.z-a.z));
}

//Перемещаем углы ограничивающего параллелепипеда
void Volume::translate(glm::vec3 shift){
  a += shift;
  b += shift;
}

Если я сгенерирую n комнат, то состоянием системы является конфигурация ограничивающих параллелепипедов в 3D-пространстве.

Нужно заметить что возможные конфигурации для этих объёмов бесконечны, но счётно бесконечны (они могут быть перечислены за бесконечное количество времени)!

//Вектор комнат (состояние моей системы!)
std::vector<Volume> rooms;

//Создаём N объёмов
for(int i = 0; i < n; i++){
  //Новый объём
  Volume x;
  x.a = glm::vec3(0);
  x.b = glm::vec3(rand()%4+5); //Случайный огранчивающий параллелепипед

  //Добавляем доступные комнаты.
  rooms.push_back(x);
}

//...

Множество возможных переходов будет являться сдвигом комнат в одном из шести направлений пространства на один шаг, в том числе и отсутствие перехода:

//...  

//Возможное множество преобразований
  std::array<glm::vec3, 7> moves = {
    glm::vec3( 0, 0, 0),  //Отсутствие хода тоже возможно!
    glm::vec3( 1, 0, 0),
    glm::vec3(-1, 0, 0),
    glm::vec3( 0, 1, 0),
    glm::vec3( 0,-1, 0),
    glm::vec3( 0, 0, 1),
    glm::vec3( 0, 0,-1),
  };

//...

Примечание: важно, что мы сохраняем системе возможность оставаться в её текущем состоянии!

Функция затрат

Я хотел, чтобы объёмы в 3D-пространстве вели себя как «магниты», то есть:

• Если их объёмы пересекаются, то это плохо.
• Если их поверхности касаются, то это хорошо.
• Если они совсем не касаются, то это плохо.
• Если они касаются пола, это хорошо.

Для двух кубоидов в 3D-пространстве мы можем легко определить ограничивающий параллелепипед:

Volume boundingBox(Volume v1, Volume v2){
  //Новый ограничивающий объём
  Volume bb;

  //Определяем нижний угол
  bb.a.x = (v1.a.x < v2.a.x)?v1.a.x:v2.a.x;
  bb.a.y = (v1.a.y < v2.a.y)?v1.a.y:v2.a.y;
  bb.a.z = (v1.a.z < v2.a.z)?v1.a.z:v2.a.z;

  //Определяем верхний угол
  bb.b.x = (v1.b.x > v2.b.x)?v1.b.x:v2.b.x;
  bb.b.y = (v1.b.y > v2.b.y)?v1.b.y:v2.b.y;
  bb.b.z = (v1.b.z > v2.b.z)?v1.b.z:v2.b.z;

  return bb;
}

При помощи ограничивающего параллелепипеда объёмов мы можем вычислить один 3D-вектор, дающий мне информацию о пересечении двух объёмов.

Если длина параллелепипеда вдоль одной стороны больше, чем сумма длин двух объёмов вдоль этой стороны, то с этой стороны они не касаются. Если они равны, то поверхности касаются, а если меньше, то объёмы пересекаются.

//Вычисляем пересечение объёмов в 3 направлениях
glm::vec3 overlapVolumes(Volume v1, Volume v2){
  //Вычисляем ограничивающий параллелепипед для двух объёмов
  Volume bb = boundingBox(v1, v2);

  //Вычисляем пересечение
  glm::vec3 ext1 = glm::abs(v1.b - v1.a);  //Размеры v1 в 3 направлениях
  glm::vec3 ext2 = glm::abs(v2.b - v2.a);  //Размеры v2 в 3 направлениях
  glm::vec3 extbb = glm::abs(bb.b - bb.a); //Размеры ограничивающего параллелепипеда

  //Вычисление пересечения
  return ext1 + ext2 - extbb;
}

Этот код используется для вычисления количества величин, для которых я образую взвешенную сумму, которая в конечном итоге используется как затраты.

int volumeCostFunction(std::vector<Volume> rooms){
  //Метрика
  int metric[6] = {
    0, //Положительный объём пересечения
    0, //Отрицательный объём пересечения
    0, //Площадь касающихся по вертикали поверхностей
    0, //Площадь касающихся по горизонтали поверхностей
    0, //Величина площади, касающейся пола
    0};//Величина объёма ниже пола

  int weight[6] = {2, 4, -5, -5, -5, 5};

  //Вычисляем энергию конфигурации комнат
  for(unsigned int i = 0; i < rooms.size(); i++){

    //Сравниваем метрики с другими комнатами
    for(unsigned int j = 0; j < rooms.size(); j++){
      //Если это та же комната, то пропускаем.
      if(i == j) continue;

      //Вычисляем пересечение между двумя объёмами.
      glm::vec3 overlap = overlapVolumes(rooms[i], rooms[j]);

      //Положительный объём пересечения
      glm::vec3 posOverlap = glm::clamp(overlap, glm::vec3(0), overlap);
      metric[0] += glm::abs(posOverlap.x*posOverlap.y*posOverlap.z); //Игнорируем отрицательные значения

      //Отрицательный объём пересечения
      glm::vec3 negOverlap = glm::clamp(overlap, overlap, glm::vec3(0));
      metric[1] += glm::abs(negOverlap.x*negOverlap.y*negOverlap.z); //Игнорируем отрицательные значения

      //Контакт верхней поверхности
      if(overlap.y == 0){
        metric[2] += overlap.x*overlap.z;
      }
      //Контакт боковой поверхности (X)
      if(overlap.x == 0){
        //Он всё равно может быть равен 0, если касаются углы, т.е. overlap.z = 0
        metric[3] += overlap.z*overlap.y;
      }
      //Контакт боковой поверхности (Z)
      if(overlap.z == 0){
        //Он всё равно может быть равен 0, если касаются углы, т.е. overlap.x = 0
        metric[4] += overlap.x*overlap.y;
      }
    }

    //Нам нужно знать, касается ли какая-то из комнат пола.
    if(rooms[i].a.y == 0){
      //Если комнаты больше, то важнее, что они касаются пола.
      metric[4] += rooms[i].a.x*rooms[i].a.z;
    }

    //Проверяем, есть ли объём под полом!
    if(rooms[i].a.y < 0){
      //Проверяем, не находится ли под поверхностью весь объём
      if(rooms[i].b.y < 0){
        metric[5] += rooms[i].getVol();
      }
      else{
        metric[5] += abs(rooms[i].a.y)*(rooms[i].b.z-rooms[i].a.z)*(rooms[i].b.x-rooms[i].a.x);
      }
    }
  }

  //Возвращаем Metric * Weights
  return metric[0]*weight[0] + metric[1]*weight[1] + metric[2]*weight[2] + metric[3]*weight[3] + metric[4]*weight[4] + metric[5]*weight[5];
}

Примечание: «положительный объём пересечения» означает, что объёмы на самом деле пересекаются. «Отрицательный объём пересечения» означает, что они совсем не касаются и пересечение задается объёмом в пространстве, расположенным между двумя ближайшими точками двух кубоидов в 3D-пространстве.

Веса выбираются таким образом, чтобы отдавать приоритет одним вещам и штрафовать другие. Например, здесь я сильно штрафую комнаты, находящиеся под полом, а также повышаю приоритет тех, чьи площади поверхностей касаются (больше, чем я штрафую пересечение объёмов).

Я формирую затраты для всех пар комнат, игнорируя комнаты, спаренные с самими собой.

Поиск решения с низкими затратами

Схождение выполняется так, как описано в псевдокоде. При выполнении перехода я двигаю только одну комнату за раз. Это значит, что при n комнатах и 7 возможных перехода мне нужно вычислить 7*n вероятностей, и я выполняю выборку из всех них, двигая только ту комнату, которая вероятно наиболее предпочтительна.

  //Вычислительная температура
  float T = 250;

  while(T > 0.1){
    //Массив вероятностей перехода
    std::vector<std::array<double, moves.size()>> probabilities;
    
    //Вычисляем текущую энергию (затраты)
    int curEnergy = volumeCostFunction(rooms);

    //Выполняем все возможные преобразования и вычисляем энергию...
    for(int i = 0; i < n; i++){
      //Создаём массив для хранения 
      std::array<double, moves.size()> probability;

      //Обходим в цикле все возможные множества перемещений, вычисляем вероятность этого преобразования
      for(unsigned int m = 0; m < moves.size(); m++){
        //Перемещаем комнату на ход и вычисляем энергию новой конфигурации.
        rooms[i].translate(moves[m]);

        //Вычисляем вероятность перехода с помощью разности энергий!
        probability[m] = exp(-(double)(volumeCostFunction(rooms) - curEnergy)/T);

        //Выполняем переход обратно
        rooms[i].translate(-moves[m]);
      }

      //Складываем вероятности для этой комнаты в вектор
      probabilities.push_back(probability);
    }

    //Функция разбиения (коэффициент нормализации)
    double Z = 0;
    for(unsigned int i = 0; i < probabilities.size(); i++){
      for(unsigned int j = 0; j < probabilities[i].size(); j++){
        Z += probabilities[i][j];
      }
    }

    //Нормализуем вероятности
    for(unsigned int i = 0; i < probabilities.size(); i++){
      for(unsigned int j = 0; j < probabilities[i].size(); j++){
        probabilities[i][j] /= Z;
      }
    }

    //Вычисляем функцию накапливаемой плотности (CDF) (для сэмпирования)
    std::vector<double> cdf;
    for(unsigned int i = 0; i < probabilities.size(); i++){
      for(unsigned int j = 0; j < probabilities[i].size(); j++){
        if(cdf.empty()) cdf.push_back(probabilities[i][j]);
        else cdf.push_back(probabilities[i][j] + cdf.back());
      }
    }

    //Генерируем случайную величину с равномерным распределением
    std::random_device rd;
    std::mt19937 e2(rd());
    std::uniform_real_distribution<> dist(0, 1);
    double uniform = dist(e2);
    int sampled_index = 0;

    //Выполняем выборку из CDF
    for(unsigned int i = 0; i < cdf.size(); i++){
      //Если мы превосходим значение равномерности, то результат найден...
      if(cdf[i] > uniform){
        sampled_index = i;
        break;
      }
    }

    //Определяем сэмплируемую комнату и ход
    int _roomindex = sampled_index/moves.size();
    int _moveindex = sampled_index%moves.size();

    //Выполняем ход
    rooms[_roomindex].translate(moves[_moveindex]);

    //Снижаем T
    T *= 0.99; 

    //Повторяем !!!
  }
//Готово!!

//...

Сэмплирование выполняется образованием кумулятивной функции распределения по функции распределения масс всех возможных переходов; эта операция называется «сэмплированием обратного преобразования».

Это выполняется образованием накопленной суммы вероятностей переходов, что даёт нам функцию распределения (cumulative distribution function, CDF). Для сэмплирования мы генерируем случайную величину с равномерным распределением в интервале от 0 и 1. Так как первый элемент CDF равен нулю, а последний единице, нам просто нужно найти «в каком индексе массива CDF находится наша сэмплируемая величина с равномерным распределением», и этот будет индексом сэмплированного перехода. Вот иллюстрация:


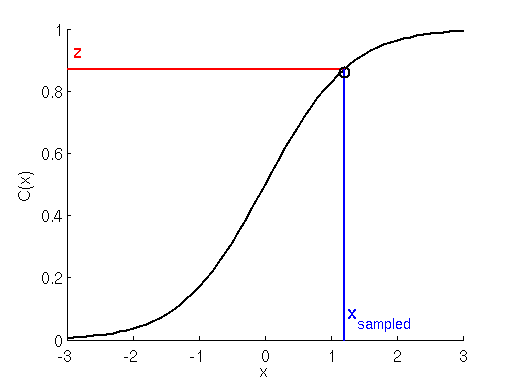
Вместо непрерывной функции могут быть дискретные шаги. Подробнее можно прочитать здесь.

Кроме того, у меня есть данные объёмов комнат в 3D-пространстве!

Я использую их для генерации «схемы» при помощи класса blueprint, применяя тему к известным объёмным данным. Так дома получают свой внешний вид. Класс blueprint описан в предыдущей статье [здесь] ([перевод] на Хабре). Полную генерацию дома из данных объёмов см. в исходном коде.

Результаты

Результаты для такого обобщённого метода оказываются довольно неплохими. Единственное, что мне пришлось настроить — это правильные веса приоритетов и штрафов в функции затрат.


Несколько примеров генерации зданий при помощи этого алгоритма и применённой к ним темы.


Вид сбоку (других зданий).

Само схождение выполняется очень быстро, особенно для небольшого количества комнат (3-5), потому что вычисления ограничивающих параллелепипедов и оценка функции затрат очень просты.

В текущей версии у домов нет дверей и окон, но это больше вопрос интерпретации 3D-данных объёмов, а не задача для алгоритма MCMC.

Иногда метод даёт некрасивые результаты, ведь это стохастический процесс, поэтому перед размещением здания в мире нужно выполнять проверки его правильности, особенно если функция затрат не очень надёжна. Я подозреваю, что некрасивость в основном возникает на первых нескольких шагах, когда температура высока.

Обычно дефекты проявляются как отделённые от здания комнаты или комнаты. висящие в воздухе (на высоких сваях).

Расширения и другие системы

Очевидно, что мою методику с 3D-объёмами легко перенести в 2D-мир, просто снизив размерность задачи на один.

То есть её можно применять для таких задач, как процедурная генерация подземелий или комнат в 2D-играх с видом сверху — прикрепление комнат друг к другу использует функцию затрат, похожую на описанную выше.

Возможный способ сделать генерацию более интересной заключается в том, чтобы сначала генерировать граф комнат, каждая из которых имеет свой тип, а затем задать функцию затрат, стимулирующую соединённость комнат, соединённых в графе по физическим поверхностям.

Сам граф можно сгенерировать с помощью алгоритма MCMC, где создание и уничтожение связей между комнатами будут считаться отдельными переходами, стимулирующими соединения между комнатами определённых типов (спальни с большей вероятностью соединяются с коридорами и с меньшей вероятностью с внешней средой, и т.п.).

Другие возможные применения:

• Генерация лабиринтов; затраты задаются в зависимости от извилистости лабиринта, а переходами являются размещение/удаление стен или коридоров.
• Сети дорог, установка и разрушение соединений между узлами графа на основании расстояния, рельефа или других факторов, используемых как затраты.
• Вероятно, многие другие!

Интересное примечание: имитация отжига и алгоритмы MCMC могут применяться для таких задач, как «задача коммивояжёра», знаменитой NP-трудной задачи. Состояние системы — это маршрут, переходы могут быть переключением узлов маршрута, а затраты — полным расстоянием!

Применение для Task-ботов

Надеюсь, что благодаря этой системе task-боты смогут в будущем создавать собственные знания в соответствии со своими потребностями.

Вот видео того, как бот строит дом, сгенерированный этим алгоритмом:


Создание черновика здания выполняется почти мгновенно (он готов, когда бот поворачивает за угол). Постройка занимает гораздо больше. Без дверей бот запирает себя внутри здания (иногда этого не происходит) и процесс строительства продолжается телепатически. Также можно посмотреть, как здание выглядит изнутри. Так как бот пытается воспользоваться поиском пути и ему это не удаётся, ближе к концу процесс становится слегка тормозным. Эту проблему нужно как-то решить, но я пока не знаю, как.