Когда-то при начале программирования мне часто требовалось изобразить линию известной длины под углом. А чтобы рассчитать координаты, использовались функции, которые принимают аргументы в радианах. Помнится, в той среде программирования не было предопределённых констант, без запоминания числа пи было не обойтись.
Число пи очень подходит чтобы запомнить какие-нибудь цифры. Оно достаточно известно, имеет практический смысл (хотя на практике достаточно дроби 355/113), и достаточно непредсказуемый порядок, чтобы именно помнить, а не выводить. И оно никогда не изменится.
И вот мы запомнили пару-тройку десятков цифр. Однако, что делать, если нам надо срочно себя проверить, а рядом компьютер без интернета, но с офисными программами? Сотня цифр просто так нигде не хранится.
Но оказывается, можно построить такую таблицу, которая рассчитает любое количество цифр (я проверял до тысячи). И это достаточно просто. В общем, теперь важнее запомнить как сделать такую таблицу, вместо того чтобы запоминать сами цифры.
О том, что такие расчеты возможны и примерную схему расчетов я узнал из статьи «Краник», или алгоритм для поиска цифр числа Пи. Ещё статья Вычисление N-го знака числа Пи без вычисления предыдущих по теме.
Берём количество нужных нам цифр и умножаем на 3,5, получим сколько строк данных нам надо использовать. Почему умножаем на 3,5? Просто, четвёрки хватит, а тройки нет. В статье «Краник» коэффициент 10/3.
Используется формула
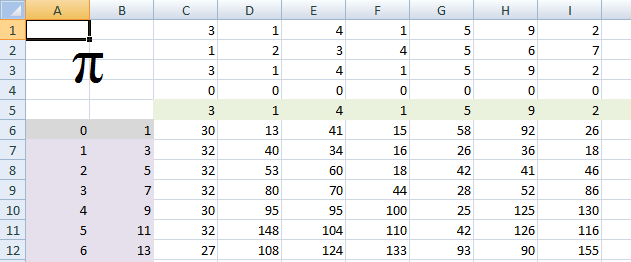
В каждой строке есть числитель, есть знаменатель, и оперирование через этот числитель и знаменатель остатками с других строк, с формированием новых остатков. Зависимость и вертикальная и горизонтальная. На верхушке получается цифра. Сколько нам надо цифр, столько будет и колонок. Цифру которая получится, нужно будет ещё обработать, так как она может быть больше 9, и тогда нужно перенести разряд вперёд. Соответственно, и принять разряд из следующей колонки тоже нужно.
Будем делать в экселе. Функции используются очень простые: «ОСТАТ» для остатка деления и «ЦЕЛОЕ» для округления. Сначала вручную пишется формульное ядро на две строки, шесть столбиков. Потом формулы растягиваются на требуемое количество строк, затем переставляем некоторые блоки из одних столбцов в другие, и затем один столбец растягиваем вширь. Читаем цифры.
Итак, составляем ядро.
Первые пять строк будут использоваться для оформления цифр. Дальше две строчки ядра мы заполним вручную. Первая из них как бы завершает расчёты для данной цифры, а вторая может быть «растянута» на все остальные.
В шестой строке пишем начальные числитель и знаменатель: A6:«0», B6:«1». Я для себя ещё и в серый цвет их крашу. В колонке D вводим начальный остаток, который у нас 2. D6:«2», D7:«2». Первоначальный остаток я тоже крашу в серый. Теперь надо посчитать сумму. С6:"=D6*10+F6". И тут же её остаток от деления на десять. E6:"=ОСТАТ(C6;10)".
Прежде чем заполнить последнюю колонку ядра, нужно всё таки заполнить числитель и знаменатель второй строки. Числитель растёт на 1, а знаменатель растёт на 2. A7:"=A6+1". B7:"=B6+2". Числитель и знаменатель я покрасил сиреневым. В C7 просто копируем из C6. Понятно, что не текст формулы, а значение ячейки. Тогда ссылочные кординаты пересчитаются. С7:"=D7*10+F7". В ячейке E7 будет считаться остаток, но не по модулю 10, а по модулю знаменателя, который B7. E7:"=ОСТАТ(C7;$B7)".
Здесь надо очень внимательно отнестись к знаку $. Когда формулы «растягиваются» на диапазон, то все её ссылки для смещённых ячеек тоже сдвигаются. А если нам надо при сдвиге обращаться в ту же колонку что и первоначальная колонка? Тогда знак $ фиксирует координату. Знаменатель у нас будет всегда в колонке B, поэтому она и зафиксирована. Когда редактируешь формулу удобно фиксировать координаты по F4, можно несколько раз нажимать, чтобы не всю ячейку фиксировать, а только строку или колонку.
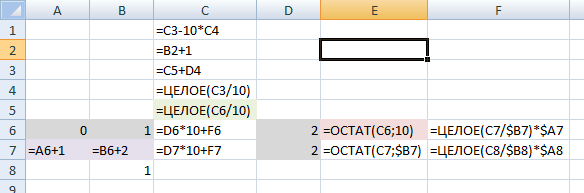
Ну вот, а теперь основная формула. F6:"=ЦЕЛОЕ(C7/$B7)*$A7".
Здесь сумма предыдущей строки делится на знаменатель предыдущей строки, округляется, и умножается на числитель предыдущей строки. «Предыдущей» — здесь имеется ввиду предыдущей по порядку расчёта, значит, та которая ниже. Колонки для числителя и знаменателя фиксированы, это обязательно. И эту формулу можно перенести на вторую строку. F7:"=ЦЕЛОЕ(C8/$B8)*$A8".
На данном этапе основное ядро уже есть, но при расчётах оно делит на ноль, поэтому для временного удобства надо поставить в B8 единицу.
Итак, посчитаем первую цифру числа Пи. С5:"=ЦЕЛОЕ(C6/10)". Первая цифра числа Пи — «2»! Не стоит удивляться. Просто, не расширенное ядро имеет слегка более низкую точность, чем можно было ожидать. В строке 4 у нас будет признак переноса, поэтому пересчитаем нашу цифру уже с переносом из следующей цифры. С3:"=C5+D4". И посчитаем новый перенос. С4:"=ЦЕЛОЕ(C3/10)".
Останется сделать нумерацию цифр. С2:"=B2+1". И саму цифру. C1:"=C3-10*C4".
Теперь можно выбирать сколько цифр получить и расширять ядро. Пусть будет 100 цифр. Значит, нам надо расширить числитель до 350, а лучше до 352. Растягиваю строку 7. Делаю так: ставлю курсор на A7. Shift+Ctrl+Right, Ctrl+Insert, Home, Shift+PageDown 9 раз, Enter!
Чтоб не было деления на ноль, в ячейке F358 ставим 0. Ctrl+End, «0», Enter. Ctrl+Home.
Теперь надо пару раз перенести блоки.
Блок D6:F358 надо перенести левее и ниже, левой колонкой в колонку B. (B359:D711). Начиная с ячейки D6: Shift+Ctrl+End, Shift+Del(или Ctrl+X), Ctrl+Down, Left, Left, Down, Shift+Ins(или Ctrl+V).
Раз.
Блок D359:D711 в колонку С. (C712:C1064) Right, Right, Ctrl+Shift+Down, Shift+Del(или Ctrl+X), Ctrl+Down, Left, Down, Shift+Ins(или Ctrl+V).
Два.
Теперь колонку C надо растянуть на столько колонок, сколько нужно цифр. Во второй строке как раз есть счётчик. После растягивания до колонки CX в первой строке будет сто цифр числа пи. Получилось.
Число пи очень подходит чтобы запомнить какие-нибудь цифры. Оно достаточно известно, имеет практический смысл (хотя на практике достаточно дроби 355/113), и достаточно непредсказуемый порядок, чтобы именно помнить, а не выводить. И оно никогда не изменится.
И вот мы запомнили пару-тройку десятков цифр. Однако, что делать, если нам надо срочно себя проверить, а рядом компьютер без интернета, но с офисными программами? Сотня цифр просто так нигде не хранится.
Но оказывается, можно построить такую таблицу, которая рассчитает любое количество цифр (я проверял до тысячи). И это достаточно просто. В общем, теперь важнее запомнить как сделать такую таблицу, вместо того чтобы запоминать сами цифры.

О том, что такие расчеты возможны и примерную схему расчетов я узнал из статьи «Краник», или алгоритм для поиска цифр числа Пи. Ещё статья Вычисление N-го знака числа Пи без вычисления предыдущих по теме.
Берём количество нужных нам цифр и умножаем на 3,5, получим сколько строк данных нам надо использовать. Почему умножаем на 3,5? Просто, четвёрки хватит, а тройки нет. В статье «Краник» коэффициент 10/3.
Используется формула
В каждой строке есть числитель, есть знаменатель, и оперирование через этот числитель и знаменатель остатками с других строк, с формированием новых остатков. Зависимость и вертикальная и горизонтальная. На верхушке получается цифра. Сколько нам надо цифр, столько будет и колонок. Цифру которая получится, нужно будет ещё обработать, так как она может быть больше 9, и тогда нужно перенести разряд вперёд. Соответственно, и принять разряд из следующей колонки тоже нужно.
Будем делать в экселе. Функции используются очень простые: «ОСТАТ» для остатка деления и «ЦЕЛОЕ» для округления. Сначала вручную пишется формульное ядро на две строки, шесть столбиков. Потом формулы растягиваются на требуемое количество строк, затем переставляем некоторые блоки из одних столбцов в другие, и затем один столбец растягиваем вширь. Читаем цифры.
Итак, составляем ядро.
Первые пять строк будут использоваться для оформления цифр. Дальше две строчки ядра мы заполним вручную. Первая из них как бы завершает расчёты для данной цифры, а вторая может быть «растянута» на все остальные.
В шестой строке пишем начальные числитель и знаменатель: A6:«0», B6:«1». Я для себя ещё и в серый цвет их крашу. В колонке D вводим начальный остаток, который у нас 2. D6:«2», D7:«2». Первоначальный остаток я тоже крашу в серый. Теперь надо посчитать сумму. С6:"=D6*10+F6". И тут же её остаток от деления на десять. E6:"=ОСТАТ(C6;10)".
Прежде чем заполнить последнюю колонку ядра, нужно всё таки заполнить числитель и знаменатель второй строки. Числитель растёт на 1, а знаменатель растёт на 2. A7:"=A6+1". B7:"=B6+2". Числитель и знаменатель я покрасил сиреневым. В C7 просто копируем из C6. Понятно, что не текст формулы, а значение ячейки. Тогда ссылочные кординаты пересчитаются. С7:"=D7*10+F7". В ячейке E7 будет считаться остаток, но не по модулю 10, а по модулю знаменателя, который B7. E7:"=ОСТАТ(C7;$B7)".
Здесь надо очень внимательно отнестись к знаку $. Когда формулы «растягиваются» на диапазон, то все её ссылки для смещённых ячеек тоже сдвигаются. А если нам надо при сдвиге обращаться в ту же колонку что и первоначальная колонка? Тогда знак $ фиксирует координату. Знаменатель у нас будет всегда в колонке B, поэтому она и зафиксирована. Когда редактируешь формулу удобно фиксировать координаты по F4, можно несколько раз нажимать, чтобы не всю ячейку фиксировать, а только строку или колонку.
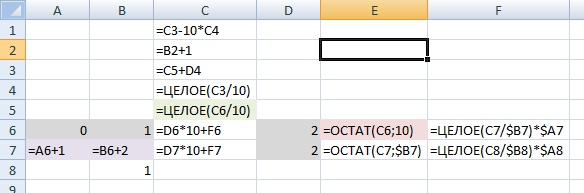
Ну вот, а теперь основная формула. F6:"=ЦЕЛОЕ(C7/$B7)*$A7".
Здесь сумма предыдущей строки делится на знаменатель предыдущей строки, округляется, и умножается на числитель предыдущей строки. «Предыдущей» — здесь имеется ввиду предыдущей по порядку расчёта, значит, та которая ниже. Колонки для числителя и знаменателя фиксированы, это обязательно. И эту формулу можно перенести на вторую строку. F7:"=ЦЕЛОЕ(C8/$B8)*$A8".
На данном этапе основное ядро уже есть, но при расчётах оно делит на ноль, поэтому для временного удобства надо поставить в B8 единицу.
Итак, посчитаем первую цифру числа Пи. С5:"=ЦЕЛОЕ(C6/10)". Первая цифра числа Пи — «2»! Не стоит удивляться. Просто, не расширенное ядро имеет слегка более низкую точность, чем можно было ожидать. В строке 4 у нас будет признак переноса, поэтому пересчитаем нашу цифру уже с переносом из следующей цифры. С3:"=C5+D4". И посчитаем новый перенос. С4:"=ЦЕЛОЕ(C3/10)".
Останется сделать нумерацию цифр. С2:"=B2+1". И саму цифру. C1:"=C3-10*C4".
Теперь можно выбирать сколько цифр получить и расширять ядро. Пусть будет 100 цифр. Значит, нам надо расширить числитель до 350, а лучше до 352. Растягиваю строку 7. Делаю так: ставлю курсор на A7. Shift+Ctrl+Right, Ctrl+Insert, Home, Shift+PageDown 9 раз, Enter!
Чтоб не было деления на ноль, в ячейке F358 ставим 0. Ctrl+End, «0», Enter. Ctrl+Home.
Теперь надо пару раз перенести блоки.
Блок D6:F358 надо перенести левее и ниже, левой колонкой в колонку B. (B359:D711). Начиная с ячейки D6: Shift+Ctrl+End, Shift+Del(или Ctrl+X), Ctrl+Down, Left, Left, Down, Shift+Ins(или Ctrl+V).
Раз.
Блок D359:D711 в колонку С. (C712:C1064) Right, Right, Ctrl+Shift+Down, Shift+Del(или Ctrl+X), Ctrl+Down, Left, Down, Shift+Ins(или Ctrl+V).
Два.
Теперь колонку C надо растянуть на столько колонок, сколько нужно цифр. Во второй строке как раз есть счётчик. После растягивания до колонки CX в первой строке будет сто цифр числа пи. Получилось.






