Как я и говорил, я потихоньку строю очень простой, но функциональный и при этом бескомпромиссно троичный вычислитель, основанный на сбалансированной троичной системе счисления. В этой статье я описываю эмулятор моего вычислителя, который мне поможет в отладке железа. Если вам интересно, не стесняйтесь писать под него программы, я их обязательно запущу на настоящем железе как только оно будет готово! Это очень просто, Триадор понимает обычный очень примитивный императивный язык, схожий с ассемблером или brainfuck :)
— Жуткий кошмар! Нули и единицы повсюду. И кажется, я видел двойку.
— Это просто сон, Бендер. Двоек не бывает.
И ведь это не шутка, в моём троичном вычислителе действительно нет двоек! Следите за мини-сериалом о постройке моего вычислителя на ютубе, а пока железо зреет, давайте разбираться с архитектурой и писать под неё первые программы!
Описание архитектуры
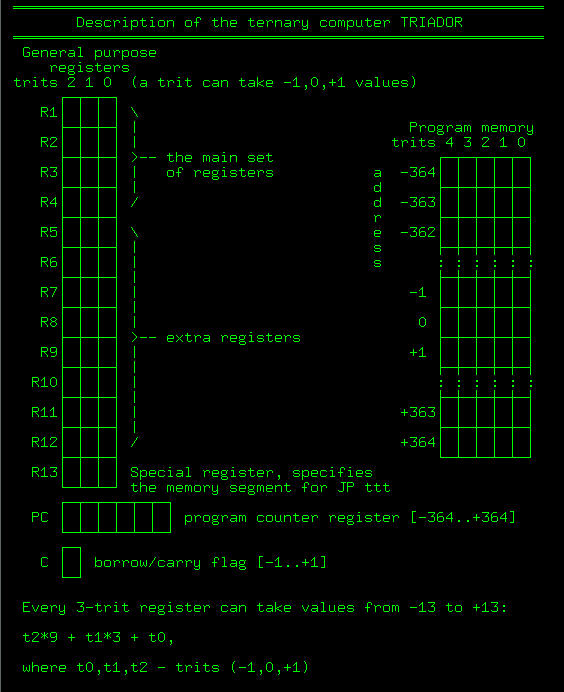
Триадор имеет трёхтритную архитектуру, это означает что его регистры могут хранить целые числа от -13 до +13. Он имеет четыре основых регистра R1-R4 и девять дополнительных регистров R5-R13. Обратите внимание, что R13 — это регистр специального назначения, он используется для выбора сегмента памяти программ (подробнее об этом ниже). Таким образом, Триадор может хранить в своей памяти 13 целых чисел из диапазона [-13..+13]. В дополнение к этому, он несёт на себе однотритный флаг переполнения/переноса и шеститритный счётчик команд. Доступная только для чтения память программ состоит из 27 сегментов по 27 инструкций каждый. Таким образом, максимальный объём программы для Триадора составляет 729 инструкций. Вот краткое описание архитектуры Триадора:
Набор инструкций
У Триадора очень ограниченный набор инструкций, он очень близок к брейнфаку в терминах удобства программирования, но предлагает гораздо более читаемый код (чуть ниже будут примеры).
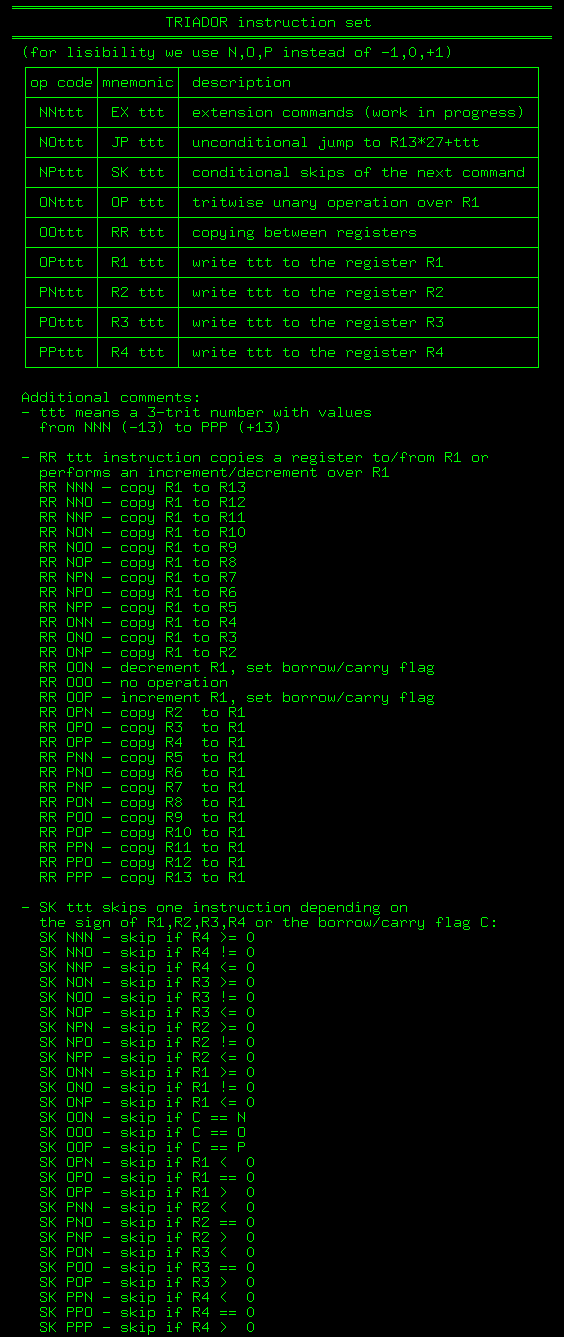
Триадор понимает 9 команд простейшего императивного языка, каждая инструкция сопровождается обязательным трёхтритным аргументом. Обратите внимание, что инструкция расширения EX ttt на данный момент интерпретируется как halt and catch fire. Вот полный список доступных команд:
Компиляция интерпретатора
git clone https://github.com/ssloy/triador.git
cd triador
mkdir build
cd build
cmake ..
make
./triador ../prog/add.txtВы также можете открыть проект в гитподе:
По открытии, редактор скомпилирует и выполнит программу на одном из примеров. Просто меняйте текст примера в редакторе и перезапускайте программу (используйте историю команд из терминала).
Спецификация файла программ
Файл с программой обязан содержать одну инструкцию на каждой строке. Инструкция обязана состоять из шести символов и находиться в начале строки. Все символы после шестого игнорируются. То есть, начало каждой строки должно содержать одну из следующих инструкций, где ttt означает трёхтритное число от NNN (-13) до PPP (+13):
- EX ttt
- JP ttt
- SK ttt
- OP ttt
- RR ttt
- R1 ttt
- R2 ttt
- R3 ttt
- R4 ttt
Интерпретатор выдаёт на экран полное состояние Триадора для каждого этапа вычислений.
Примеры программ
Обратите внимание, что Триадор не имеет интерфейсов типа мышки или даже клавиатуры. Для того, чтобы ввести данные в вычислитель, нужно использовать команды R1-R4.
Сложение
Итак, я хочу сложить два числа, записанные в регистры R2 и R3. Но Триадор не умеет складывать числа! Он умеет делать инкремент/декремент. Насколько это страшно? Да ничуть!
Давайте для начала напишем простейшую программу в знакомой вам обстановке. Я для начала предполагаю, что R2 и R3 неотрицательны. Если я у меня есть операция инкремента/декремента, то мне вполне хватит декрементировать R2 и инкрементировать R3 одновременно до тех пор, пока R2 не достигнет нуля:
int main() {
unsigned int R2 = 2;
unsigned int R3 = 11;
while (R2!=0) {
R3++;
R2--;
}
return R3;
}Отлично, а могу ли я складывать числа со знаком? Да никаких проблем, мы самую малость изменим наш код таким образом, чтобы на каждой итерации модуль числа R2 уменьшался на единицу:
int main() {
int R2 = -2;
int R3 = 13;
while (R2!=0) {
if (R2>0) R3++;
if (R2<0) R3--;
if (R2>0) R2--;
if (R2<0) R2++;
}
return R3;
}Ну, собственно, и всё. А теперь переходим непосредственно к Триадору. Добавим последний штрих: Триадор умеет инкрементировать/декрементировать исключительно регистр R1. Ну и ладно, если мы захотим прибавить к R3 единицу, скопируем его в R1, вызовем команду инкремента, и скопируем R1 назад в R3!
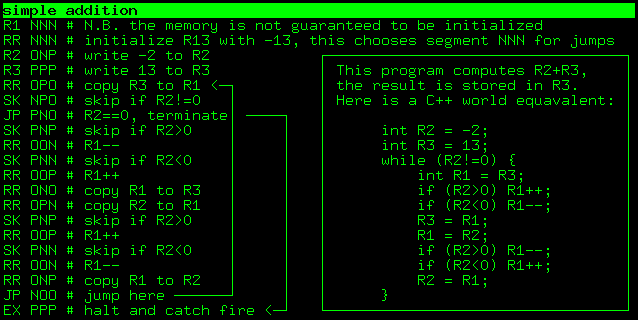
Вот очень простая программа, которая пишет два числа в регистры R2 и R3 и вычисляет их сумму. Результат хранится в R3:
Левый столбец (первые шесть символов каждой строки) — это непосредственно программа для Триадора. Счётчик команд инициализирован как NNN NNN, что равно -364 в десятичной системе и соответствует первой строке нашего файла программы. Отметим, что все символы после шестого игнорируются интерпретатором, можно считать, что это комментарии.
Вот лог запуска нашей программы:
$ ./triador ../prog/add.txt | tail -n 3
R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 C PC
11 0 11 5 0 6 -12 -2 11 8 11 -10 -13 0 -345Обратите внимание, что R3 содержит 11, результат операции -2 + 13.
Разумеется, Триадор не поддерживает циклы типа while напрямую, он использует безусловные джампы, JP, ну а ветвление обеспечивается при помощи операции SK, которая позволяет пропустить следующую за ней операцию.
Тонкий момент: обратите внимание, что команда безусловного джампа JP ttt имеет трёхтритный аргумент ttt, в то время как программный счётчик у нас шеститритный. Откуда берутся недостатющие три трита? Из регистра R13! Команда JP ttt перепрыгивает на инструкцию номер 27*R13 + ttt. Иными словами, перепрыгивает на команду номер ttt сегмента с номером, взятым из регистра R13. Самый первый сегмент памяти команд имеет номер NNN (-13), и именно поэтому первые две строчки моей программы выглядят как
R1 NNN # write -13 to R1
RR NNN # copy R1 to R13Поскольку мой код влезает целиком в один сегмент, я больше не трогаю R13, и джампы прыгают только в пределах сегмента NNN.
Сложение с контролем переполнения
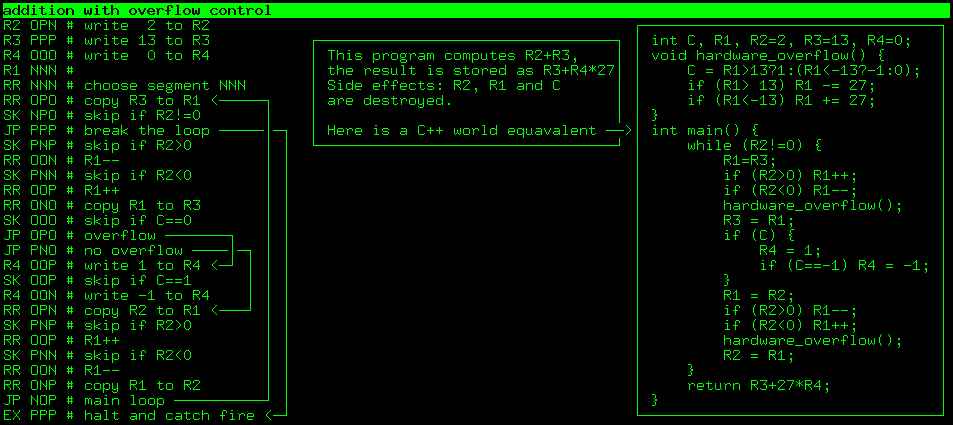
Предыдущий код складывает два трёхтритных числа, но ведь сумма двух трёхтритных чисел может не влезть в три трита памяти. Поэтому давайте напишем программу, которая складывает два трёхтритных числа, но результат будет шеститритным. Следующая программа складывает регистры R2 и R3, и записывает результат в регистры R3 и R4: результат равен R3 + R4*27, то есть, R4 может быть равен -1, 0 or 1.
$ ./triador ../prog/add-with-overflow-control.txt |tail -n 3
R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 C PC
-12 0 -12 1 -9 2 -12 -6 4 5 6 7 -13 0 -338Обратите внимание, что R3 + 27 * R4 равно 15, результату операции 2+13. По сравнению с предыдущей программой я всего-навсего добавил запись в регистр R4 флага переполнения C:
[...]
SK OOO # skip if C==0
JP OPO # overflow ───────┐
JP PNO # no overflow ────│─┐
R4 OOP # write 1 to R4 <─┘ │
SK OOP # skip if C==1 │
R4 OON # write -1 to R4 │
RR OPN # copy R2 to R1 <───┘
[...]Шеститритное сложение
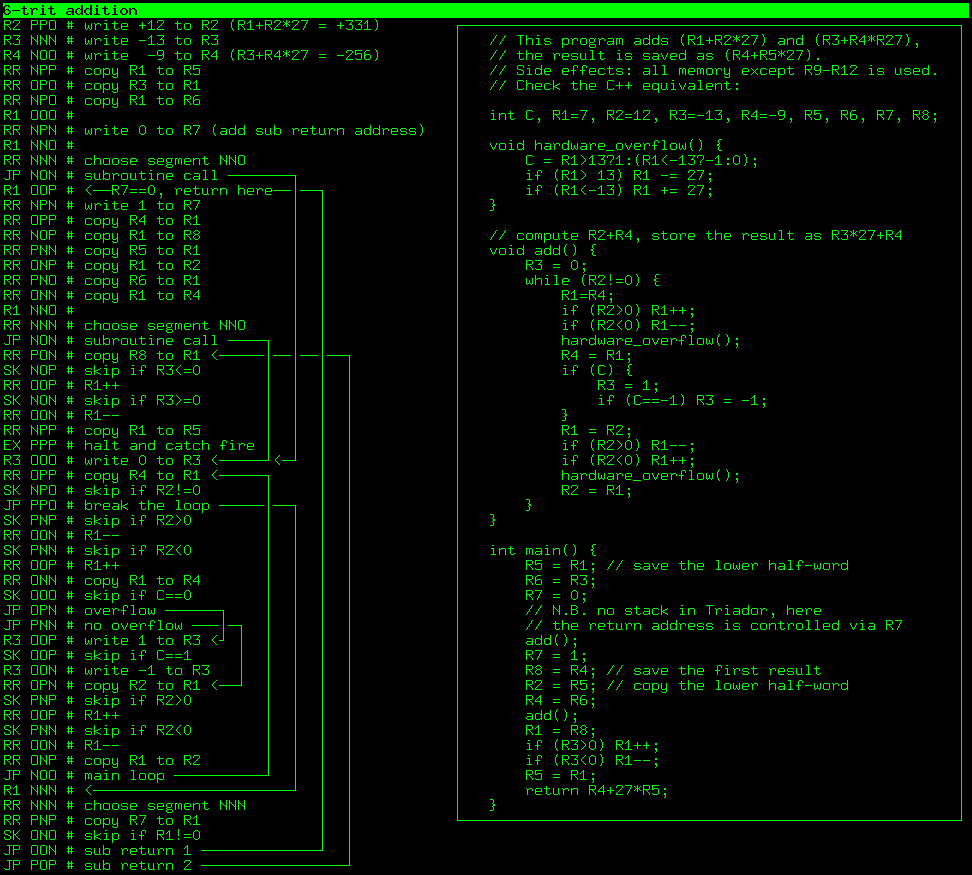
Вам кажется, что регистры с диапазоном [-13..+13] недостаточно экспрессивны? Никаких проблем, давайте введём тип данных word (на самом деле, мы его уже ввели в предыдущем примере). Эта программа записывает одно шеститритное число в регистры R1,R2 и другое в регистры R3,R4. Затем считает сумму, сохраняя в шеститритном числе R4,R5.
$ ./triador ../prog/long-add.txt |tail -n 3
R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 C PC
3 0 0 -6 3 -13 1 3 6 5 13 -2 -13 0 -335Обратите внимание, что R4+27 * R5 = 75, а мы попросили наш вычислитель посчитать 331-256. Надо ли объяснять, как работает этот код? Если вы разобрались с предыдущими двумя, думаю, ни к чему. Мы считаем сумму двух старших полуслов, затем сумму младших полуслов. Если при суммировании младших полуслов произошло переполнение, нужно добавить или отнять единицу от суммы старших полуслов. Если все эти слова трудно понимать, смотрите эквивалентный код на C++ :)
В этом коде только одна тонкость: поскольку мне дважды нужно считать сумму двух трёхтритных чисел, я пытаюсь сымитировать вызов функции. Триадор не знает стеков, триадор не знает сабрутин и адресов возврата. Но мы тоже не лыком шиты! Регистр R7 контролирует, в какое место кода нужно возвратиться из этой эрзац-сабрутины. Если очень грубо, то я храню в регистре R7 адрес возврата из функции:
[...]
SK ONO # skip if R1!=0
JP OON # sub return 1
JP POP # sub return 2Наибольший общий делитель
Разумеется, наш набор примеров был бы неполон без Евклидова алгоритма. Эта программа вычисляет наибольший общий делитель чисел, записанных в регистры R2 и R3. Результат сохраняется в регистре R2.
Давайте разберём, как она работает, для начала в привычном мире C++. Если мы предположим, что числа R2 и R3 положительны, то возможная имплементация алгоритма Евклида выглядит следующим образом:
int main() {
int R2 = 12, R3 = 8;
while (true) {
if (R2==R3) break;
if (R2>R3)
R2 = R2 - R3;
else
R3 = R3 - R2;
}
return R2;
}Насколько всем очевидно, что эта программа вычисляет наибольший общий делитель? Начнём с того, что она точно останавливается: на каждой итерации мы обновляем либо R2, либо R3; одно из них обязательно уменьшается, оставаясь положительным. Если число m делит R2 и делит R3, как это делает наибольший общий делитель, то вполне очевидно, что оно же делит и разницу R2-R3. Если это неочевидно, то запишите R2 = a m, R3 = b m и убедитесь в том, что R2-R3 = (a-b) m. Как-то так.
А что делать, если на вход мы можем получить числа со знаком? А просто взять от них модуль :) Посмотрите сами: этот код абсолютно эквивалентен предыдущему, если он на вход получит положительные числа. Ну а если отрицательные, то модуль нам поможет!
int main() {
int R2 = 12, R3 = -8;
while (true) {
if (R2<0) R2 = -R2;
if (R3>0) R3 = -R3;
if (R2==-R3) break;
int R4 = R2 + R3;
if (R4>0)
R2 = R4;
else
R3 = R4;
}
return R2;
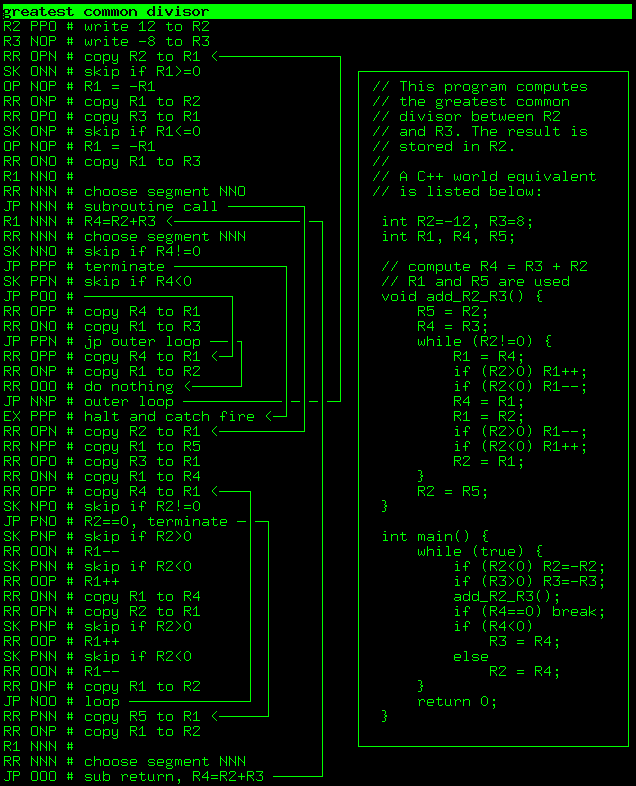
}В итоге программа для Триадора работает именно по этому принципу:
Вот лог исполнения программы:
$ ./triador ../prog/gcd.txt |tail -n 3
R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 C PC
-13 4 -4 0 4 12 13 1 -7 -9 3 4 -13 0 -338Обратите внимание, что R2 хранит 4, наибольший общий делитель 12 и -8.
Заключение
Программировать мой троичный вычислитель ничуть не сложнее, нежели какой-нибудь калькулятор типа МК-61, да и троичность никак не сказывается на принципах построения программ. Второй сезон моего микросериала будет посвящён построению арифметико-логического устройства. Ну а пока санитарные волнения не позволяют хорошо продвигаться с железом, можно отвести душу с эмулятором. Предлагайте ваши варианты решения вышеозначенных задач, предлагайте новые интересные задачи, давайте веселиться!

Stay tuned.