Привет, Хабр.
На данную статью меня вдохновила недавняя публикация Моделируем Вселенную, где автор показал весьма интересное моделирование разных космических явлений. Однако представленный там код непрост для начинающих. Я покажу как сделать физическое моделирование с помощью движка Box2D, написав всего лишь несколько строк кода.
Рискну ошибиться, но это первое описание Box2D для Python на Хабре, восполним этот пробел.
Для тех кому интересно как это работает, подробности под катом.
Box2D это бесплатная кроссплатформенная библиотека, созданная сотрудником Blizzard Erin Catto. Библиотека была представлена в 2007 году, и на сегодняшний день портирована на практически все платформы. Есть порт и для Python, его описание достаточно запутанное, но надеюсь, с помощью этой статьи все станет понятнее.
Библиотека pybox2d состоит из двух компонентов — собственно Box2D, кроссплатформенной библиотеки для физического моделирования, и отдельного модуля отрисовки, называемого Framework. Отрисовка нужна, если мы хотим видеть создаваемые объекты на экране, что достаточно удобно для нашей симуляции. Класс Framework может использовать различные способы вывода (подробнее здесь), мы будем использовать pygame. Если библиотека pygame установлена, она «подхватывается» автоматически, и ничего больше делать не нужно. Для установки достаточно ввести команду pip install Box2D pygame.
Минимально работающая программа, использующая Box2D, показана ниже. Код является кроссплатформенным, и будет работать везде, и в Linux и в Windows.
Как можно видеть, мы создаем класс Simulation, наследуемый от уже упомянутого Framework. Далее мы создаем два объекта с помощью вызова метода CreateBody. Первый это статический объект, задающий границы нашего мира. Второй объект имеет тип b2_dynamicBody, остальные параметры (форма, размер, плотность, коэффициент трения, начальная скорость) очевидны из кода. Функция Step вызывается каждый раз во время симуляции, мы воспользуемся этим в дальнейшем. Если UI не нужен, например мы делаем backend для сервера, то разумеется, класс Framework можно не использовать, но для нас это вполне удобно.
Собственно и все, запускаем программу и видим готовую симуляцию:

Как можно видеть, мы просто создали два объекта и указали их параметры. Все работает «из коробки» — сила тяжести, трение, упругость, взаимодействие тел и пр. На основе этого мы можем приступать к нашей «космической» симуляции.
К сожалению, встроенной поддержки Ньютоновской гравитации в Box2D нет, её придется добавить самостоятельно, дописав функцию Step. Для первого теста создадим два тела — планету, и вращающийся вокруг неё спутник.
Исходный код целиком:
Как можно видеть, мы «отключаем» стандартную гравитацию, установив параметр self.world.gravity в 0. Также мы добавляем параметр G, это «гравитационная постоянная» нашего виртуального мира, которая используется при расчете в методе Step. Также мы создали два объекта — спутник и планету. Здесь важно отметить параметры density (плотность) и radius. По этим параметрам библиотека Box2D сама рассчитывает массу, которая используется в расчете. Для вычисления силы взаимодействия используется обычная «школьная» формула закона тяготения Ньютона:
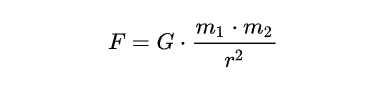
Теперь запускаем симуляцию. Первой космической скорости мы не достигли, и хотя спутник все-таки обогнул всю планету, «полетом» это назвать сложно:
Увеличиваем скорость, изменив строчку кода на linearVelocity=(28, 0):

Наш «спутник» успешно вышел на орбиту вокруг «планеты»! Если еще увеличить скорость, орбита станет эллиптической:

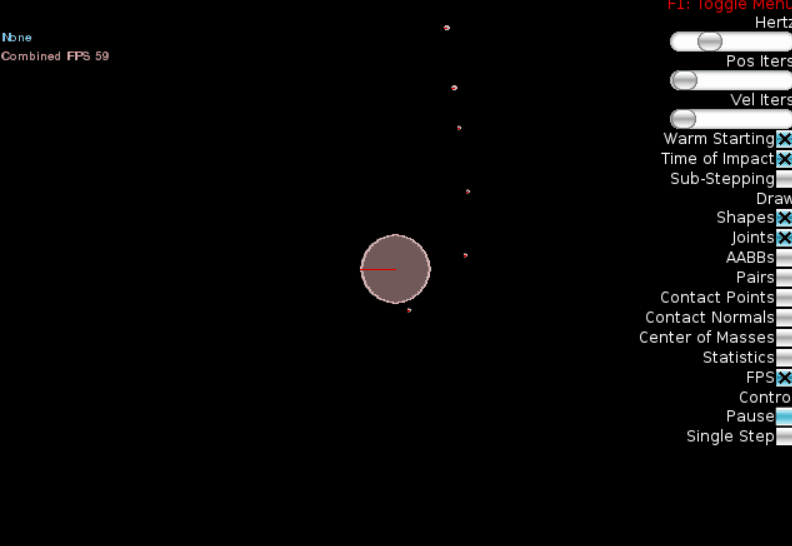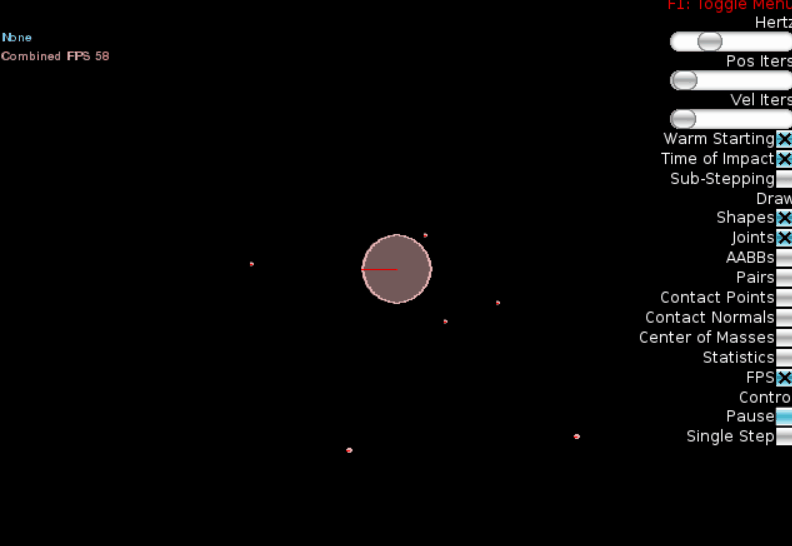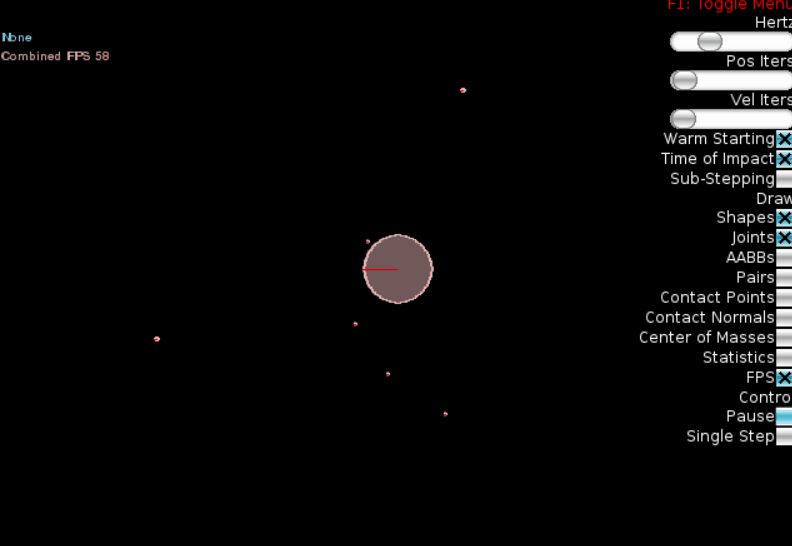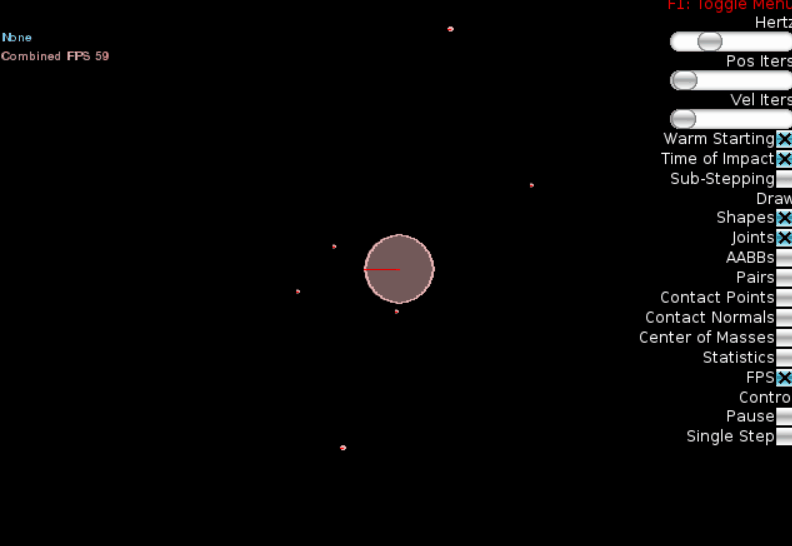
Наконец, изобразим нечто, более похожее на нашу «солнечную систему», добавив три планеты разных размеров на разных орбитах:
Результат:
Мы видим, что чем дальше планета от «солнца», тем больше её период обращения (3й закон Кеплера). К сожалению, движок Box2D не позволяет рисовать на экране треки движения, так что 1й и 2й законы Кепплера «увидеть» сложно, но можно быть уверенными, что они также выполняются.
Как можно видеть, с помощью Box2D несложные симуляции можно делать с минимальными усилиями. Разумеется, движок этот все же игровой, а не научный, так что не стоит ожидать от него корректной симуляции столкновения галактик или разлета вещества при Большом взрыве. Но некоторые закономерности посмотреть вполне любопытно.
Все задуманное в одну часть не влезло. Если оценки будут положительны, во второй части можно будет рассмотреть более нетривиальные примеры.
На данную статью меня вдохновила недавняя публикация Моделируем Вселенную, где автор показал весьма интересное моделирование разных космических явлений. Однако представленный там код непрост для начинающих. Я покажу как сделать физическое моделирование с помощью движка Box2D, написав всего лишь несколько строк кода.
Рискну ошибиться, но это первое описание Box2D для Python на Хабре, восполним этот пробел.

Для тех кому интересно как это работает, подробности под катом.
Box2D это бесплатная кроссплатформенная библиотека, созданная сотрудником Blizzard Erin Catto. Библиотека была представлена в 2007 году, и на сегодняшний день портирована на практически все платформы. Есть порт и для Python, его описание достаточно запутанное, но надеюсь, с помощью этой статьи все станет понятнее.
Введение
Библиотека pybox2d состоит из двух компонентов — собственно Box2D, кроссплатформенной библиотеки для физического моделирования, и отдельного модуля отрисовки, называемого Framework. Отрисовка нужна, если мы хотим видеть создаваемые объекты на экране, что достаточно удобно для нашей симуляции. Класс Framework может использовать различные способы вывода (подробнее здесь), мы будем использовать pygame. Если библиотека pygame установлена, она «подхватывается» автоматически, и ничего больше делать не нужно. Для установки достаточно ввести команду pip install Box2D pygame.
Минимально работающая программа, использующая Box2D, показана ниже. Код является кроссплатформенным, и будет работать везде, и в Linux и в Windows.
from Box2D.examples.framework import Framework from Box2D import * class Simulation(Framework): def __init__(self): super(Simulation, self).__init__() # Ground body self.world.CreateBody(shapes=b2LoopShape(vertices=[(20, 0), (20, 40), (-20, 40), (-20, 0)])) # Dynamic body circle = b2FixtureDef(shape=b2CircleShape(radius=2), density=1, friction=1.0, restitution=0.5) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0,30), fixtures=circle, linearVelocity=(5, 0)) def Step(self, settings): super(Simulation, self).Step(settings) if __name__ == "__main__": Simulation().run()
Как можно видеть, мы создаем класс Simulation, наследуемый от уже упомянутого Framework. Далее мы создаем два объекта с помощью вызова метода CreateBody. Первый это статический объект, задающий границы нашего мира. Второй объект имеет тип b2_dynamicBody, остальные параметры (форма, размер, плотность, коэффициент трения, начальная скорость) очевидны из кода. Функция Step вызывается каждый раз во время симуляции, мы воспользуемся этим в дальнейшем. Если UI не нужен, например мы делаем backend для сервера, то разумеется, класс Framework можно не использовать, но для нас это вполне удобно.
Собственно и все, запускаем программу и видим готовую симуляцию:

Как можно видеть, мы просто создали два объекта и указали их параметры. Все работает «из коробки» — сила тяжести, трение, упругость, взаимодействие тел и пр. На основе этого мы можем приступать к нашей «космической» симуляции.
Запускаем «спутник»
К сожалению, встроенной поддержки Ньютоновской гравитации в Box2D нет, её придется добавить самостоятельно, дописав функцию Step. Для первого теста создадим два тела — планету, и вращающийся вокруг неё спутник.
Исходный код целиком:
from Box2D import * from Box2D.examples.framework import Framework class Simulation(Framework): def __init__(self): super(Simulation, self).__init__() # Default gravity disable self.world.gravity = (0.0, 0.0) # Gravity constant self.G = 100 # Planet circle = b2FixtureDef(shape=b2CircleShape(radius=5), density=1, friction=0.5, restitution=0.5) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0,0), fixtures=circle) # Satellite circle_small = b2FixtureDef(shape=b2CircleShape(radius=0.2), density=1, friction=0.5, restitution=0.2) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0, 10), fixtures=circle_small, linearVelocity=(20, 0)) def Step(self, settings): super(Simulation, self).Step(settings) # Simulate the Newton's gravity for bi in self.world.bodies: for bk in self.world.bodies: if bi == bk: continue pi, pk = bi.worldCenter, bk.worldCenter mi, mk = bi.mass, bk.mass delta = pk - pi r = delta.length if abs(r) < 1.0: r = 1.0 force = self.G * mi * mk / (r * r) delta.Normalize() bi.ApplyForce(force * delta, pi, True) if __name__ == "__main__": Simulation().run()
Как можно видеть, мы «отключаем» стандартную гравитацию, установив параметр self.world.gravity в 0. Также мы добавляем параметр G, это «гравитационная постоянная» нашего виртуального мира, которая используется при расчете в методе Step. Также мы создали два объекта — спутник и планету. Здесь важно отметить параметры density (плотность) и radius. По этим параметрам библиотека Box2D сама рассчитывает массу, которая используется в расчете. Для вычисления силы взаимодействия используется обычная «школьная» формула закона тяготения Ньютона:
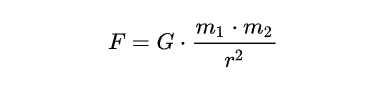
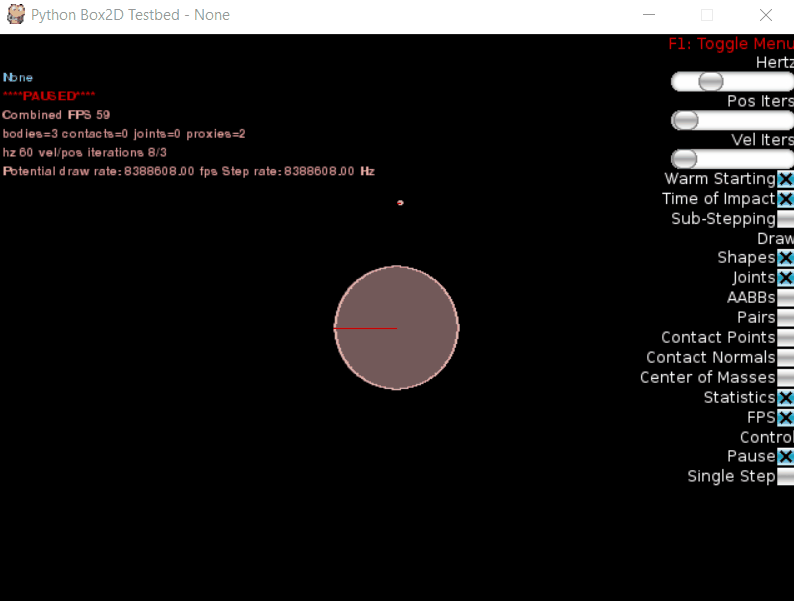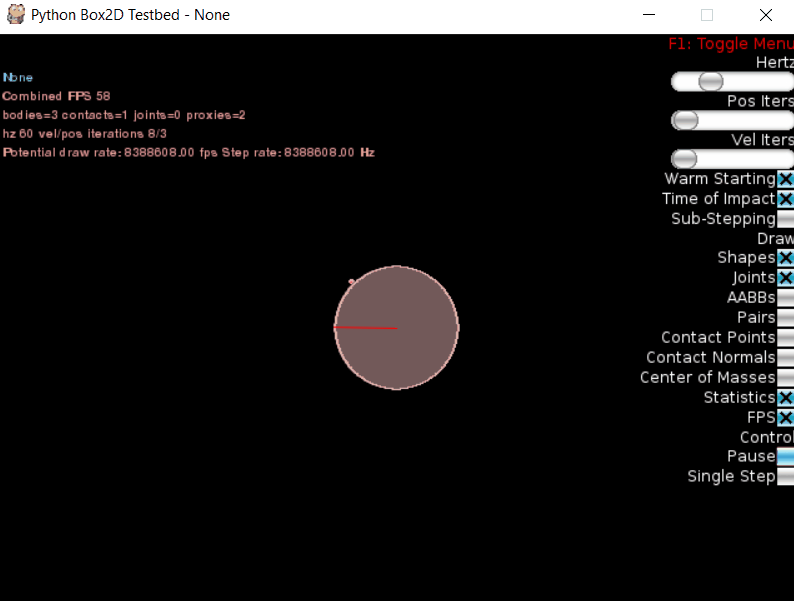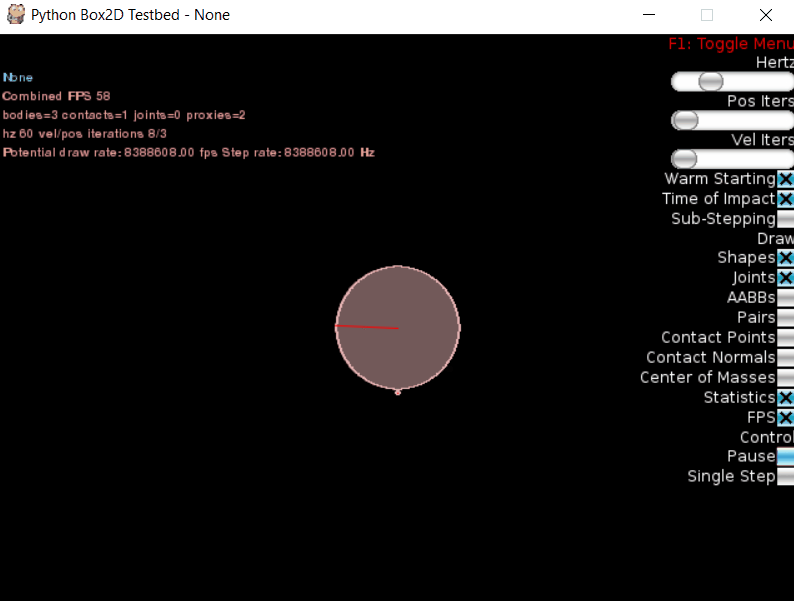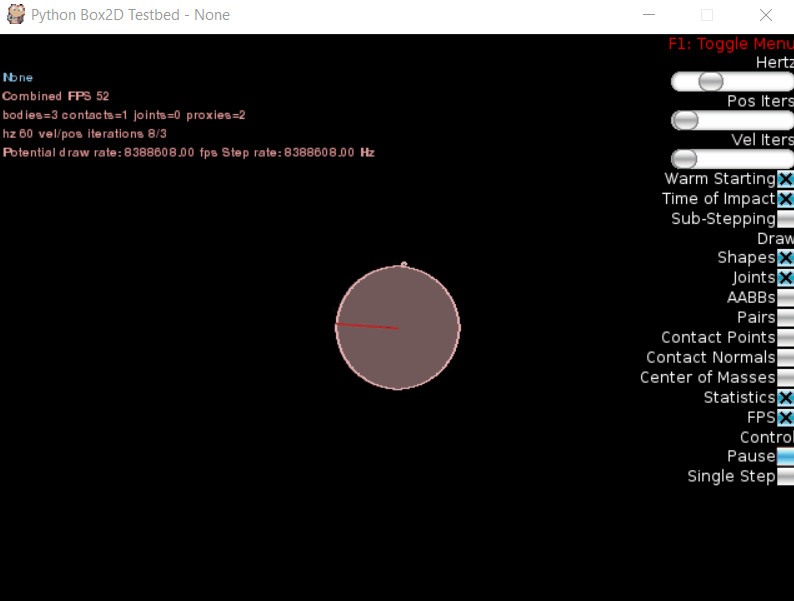
Теперь запускаем симуляцию. Первой космической скорости мы не достигли, и хотя спутник все-таки обогнул всю планету, «полетом» это назвать сложно:

Увеличиваем скорость, изменив строчку кода на linearVelocity=(28, 0):

Наш «спутник» успешно вышел на орбиту вокруг «планеты»! Если еще увеличить скорость, орбита станет эллиптической:

Наконец, изобразим нечто, более похожее на нашу «солнечную систему», добавив три планеты разных размеров на разных орбитах:
circle_small = b2FixtureDef(shape=b2CircleShape(radius=0.2), density=1, friction=0.5, restitution=0.2) circle_medium = b2FixtureDef(shape=b2CircleShape(radius=0.3), density=1, friction=1.0, restitution=0.5) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0, 6), fixtures=circle_small, linearVelocity=(37, 0)) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0, 10), fixtures=circle_small, linearVelocity=(28, 0)) self.world.CreateBody(type=b2_dynamicBody, position=b2Vec2(0, 15), fixtures=circle_medium, linearVelocity=(22, 0))
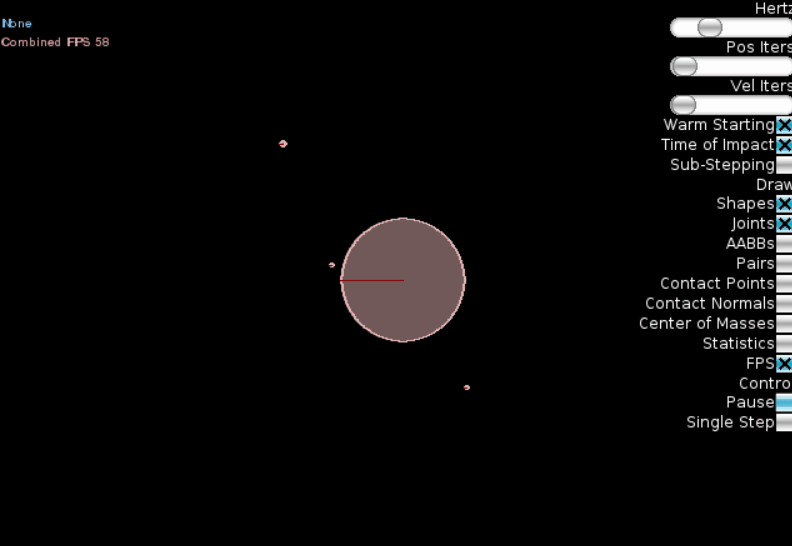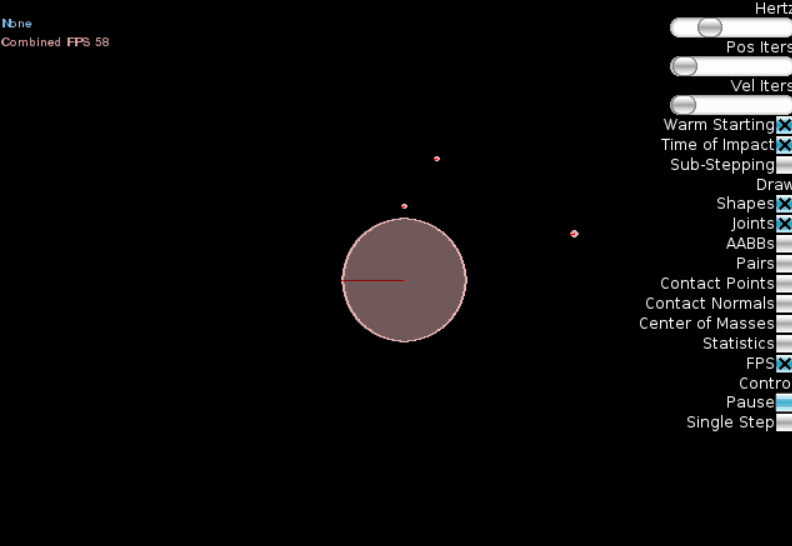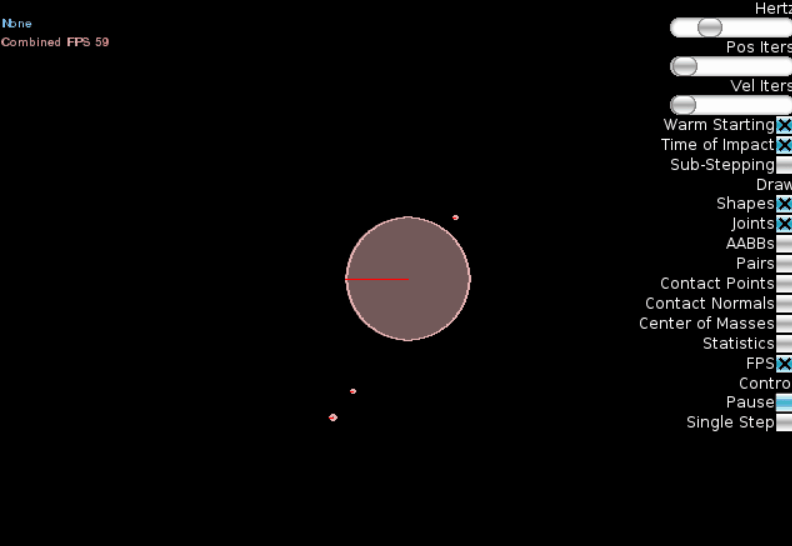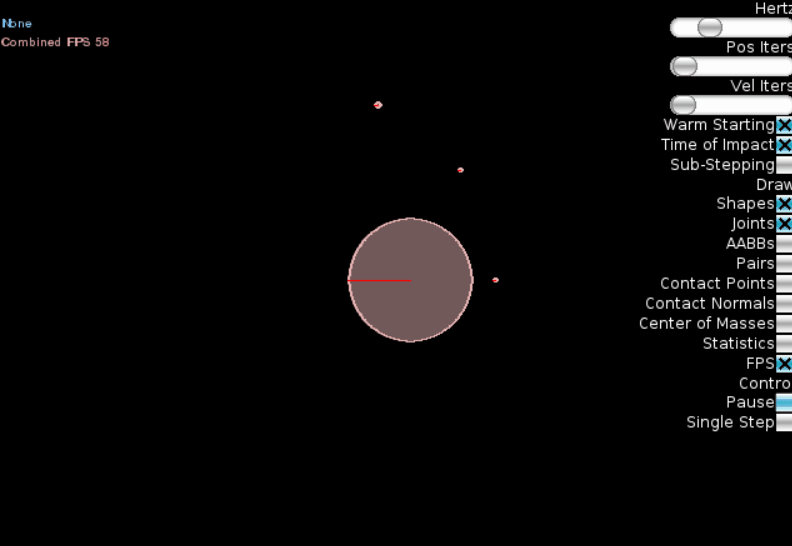
Результат:

Мы видим, что чем дальше планета от «солнца», тем больше её период обращения (3й закон Кеплера). К сожалению, движок Box2D не позволяет рисовать на экране треки движения, так что 1й и 2й законы Кепплера «увидеть» сложно, но можно быть уверенными, что они также выполняются.
Заключение
Как можно видеть, с помощью Box2D несложные симуляции можно делать с минимальными усилиями. Разумеется, движок этот все же игровой, а не научный, так что не стоит ожидать от него корректной симуляции столкновения галактик или разлета вещества при Большом взрыве. Но некоторые закономерности посмотреть вполне любопытно.
Все задуманное в одну часть не влезло. Если оценки будут положительны, во второй части можно будет рассмотреть более нетривиальные примеры.
