Предлагается вниманию пересказ статьи Core expansion: a new community detection algorithm based on neighborhood overlap, вышедшей в журнале Social Network Analysis and Mining, номер 10, 30, (2020) с нашими комментариями. В этой статье описывается новый алгоритм для выделения сообществ в графе, основанный на Jaccard index.
Заявленными преимуществами алгоритма являются детерминированность и более крупные выделяемые сообщества при хорошей скорости работы. К сожалению, нам не удалось найти авторскую реализацию данного алгоритма, но мы с коллегами не отчаялись и за выходные написали свою.
Наша имплементация написана на Java и доступна в GitHub под MIT-лицензией. Возможно использование как в качестве отдельного приложения командной строки, так и в качестве разделяемой Java-библиотеки.
В конце этой статьи мы расскажем, где и для каких целей мы анализируем графы в Райффайзенбанке.
Задача выделения сообществ
Задача выделения сообществ в графе известна давно и имеет множество практических приложений. Например, выделяя сообщества в сетях ищут и анализируют группы нейронов головного мозга. Есть ряд интересных применений в анализе, например, сетей цитирования патентных документов — это активно применяется для выделения и количественного анализа областей техники, так называемые патентные ландшафты. Есть применения для выделения сообществ в социальных сетях типа Facebook, что используется при выборе групп для целевой рекламы. На самом деле применений еще очень много и это тема для отдельной статьи.
Задача выделения сообществ существует достаточно давно и, в целом, формулируется несложно. Дан граф, и его вершины необходимо кластеризовать — разбить на группы.
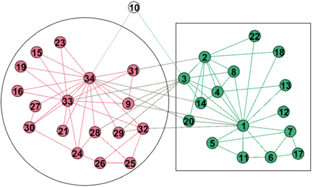
Человек, глядя, например, на известный граф, визуализирующий Zachary's karate club (картинка из оригинальной работы, ссылка и библиография в шапке) сразу поймет, что тут и правда два сообщества и примерно ясно, где идет разделение между ними. Дальше оставалось формально поставить задачу – и все, можно придумывать алгоритмы.
Одной из первых постановок задачи выделения сообществ была формализация через показатель Modularity, предложенная Newman и Girvan в начале нулевых годов. Modularity – это одна из возможных мер качества кластеризации графа. Она основана на сравнении нашего графа со случайным графом с тем же количеством вершин и ребер. Это определенный от -1 до 1 показатель, который оценивает количество ребер внутри каждого из сообществ в имеющемся графе и в графе на тех же вершинах, но со случайными ребрами.
Когда Modularity равна нулю, то это значит, что внутри наших сообществ количество ребер такое, будто мы выбрали их случайно. Если Modularity равна 1, то это значит, что наши найденные сообщества никогда не могли бы возникнуть случайно. А если этот показатель стремится к -1, значит, в случайном графе внутри нашего сообщества было бы больше ребер (мы нашли "антикластеризацию"). Я немного упростил, кому интересно может, например, найти строгую формулу в Википедии.
Есть и другие показатели "качества" выделенных нами сообществ, например, Normalized Mutual Information (далее NMI). В целом, сегодня их довольно много.
Не так давно попалась на глаза статья про Core Expansion, в которой авторы предлагают новый алгоритм для решения этой задачи. Статья показалась мне интересной и далее мы хотим представить краткий пересказ этой статьи с нашими комментариями. Дополнительно мы кратко обсудим практическую реализацию данного алгоритма и наш код на GitHub, так как, к сожалению, авторы не выложили свой код в открытый доступ.
Обсуждение подобных работ невозможно без обсуждения уже существующих алгоритмов и их недостатков. Те, кто хорошо знаком с существующими алгоритмами для выделения сообществ может смело пролистывать этот раздел.
На самом деле задача максимизации (минимизации) метрик типа Modularity является NP-трудной задачей, так как надо проверить все возможные варианты разбиения графа на сообщества. Особенно это становится интересным, когда число сообществ заранее неизвестно и его тоже надо определять. Поэтому обычно используют какую-нибудь "жадную л��гику" или эвристики и находят приближенное решение задачи.
Girvan-Newman Algorithm
Например, известный алгоритм Girvan-Newman начинает "удалять" из графа ребра по одному по принципу максимального показателя Edge Betweenness (если упрощать, то это величина, пропорциональная числу кратчайших путей, проходящих через данное ребро, и обратно пропорциональна "уникальности" этих путей).
После каждого удаления мы считаем Modularity и пересчитываем Edge Betweenness. Удалив все ребра, мы получаем историю "удалений", начиная от одного большого сообщества и заканчивая состоянием, где у нас каждая вершина в своем сообществе (удалены все ребра). Для каждого состояния в истории у нас есть показатель Modularity. Просто выбираем максимум – это и будет наша кластеризация.
По понятным причинам (сложность вычисления Edge Betweenness порядка по числу вершин, так как надо считать все кратчайшие пути в графе) работает очень медленно, даже для графов средних размеров, а графы на сотнях тысяч вершин этот алгоритм вообще не способен переварить.
Louvain Algorithm
Другой известный алгоритм, который на сегодня является самым популярным алгоритмом выделения сообществ, — это Louvain Community Detection Algorithm. Суть заключается в том, что при перемещении отдельной вершины из одного сообщества в другое нам не надо пересчитывать полностью Modularity, достаточно лишь пересчитать вклад этой вершины.
Другая подмеченная авторами оригинальной работы особенность пр��мой оптимизации Modularity заключается в том, что жадный процесс генерирует очень много маленьких сообществ, но практически не выделяет большие. Отсюда авторами был предложен алгоритм:
- Помещаем каждую вершину в свое собственное сообщество.
- Жадно пытаемся двигать вершины из одного сообщества в другое, на основе максимизации Modularity.
- Когда никакое перемещение больше не дает прирост Modularity, мы формируем новый взвешенный граф, где вершины — это сообщества с шага 2, а ребра пересчитываются на основе количества ребер между вершинами сообществ.
- Повторяем шаг 1 для нового графа.
В результате значительно увеличивается вычислительная эффективность, а итоговые сообщества получаются большими и хорошими. Масштабируется на графы с миллионами и десятками миллионов вершин (может, и больше, я не пробовал).
Те, кто пробовал алгоритм Louvain в деле, знают, что у него есть ряд проблем:
- Ему свойственно "разбивать" сильно связанные сообщества. По крайней мере, на force-directed визуализациях они кажутся таковыми.
- Он является строго детерминированным, что порождает дополнительные проблемы. Например, если мы используем результаты кластеризации в алгоритмах машинного обучения как признак.
- Алгоритм Louvain обязательно будет пытаться кластеризовать весь граф, не оставляя возможности существования вершин "выбросов", которые лучше не относить ни к одному сообществу. Это сложно назвать недостатком, скорее особенность, которую нужно учитывать.
На самом деле, есть модификации Louvain алгоритма, которые частично решают эти проблемы. Например, Leiden решает проблему разбиения связных сообществ, а DAOC сохраняет идею, но детерминирован. Но, не смотря на это, авторы статьи, которую мы рассматриваем, противопоставляли свой алгоритм именно Louvain. Это их право, мы лишь позволим себе отметить некоторую "нечестность" такого сравнения.
Core Expansion
Перейдем к авторскому алгоритму. Сразу оговоримся, что алгоритм применим лишь для ненаправленных, не взвешенных графов. Авторы в конце статьи пишут, что они попробуют его расширить на большее количество случаев, но пока as is. От себя добавлю – расширение на взвешенные графы кажется нетрудным, а вот с направленными могут быть проблемы. Также хочется отметить, что сама идея и алгоритм кажутся до ужаса простыми, но так как работа опубликована в хорошем рецензируемом журнале, то, скорее всего, это ложное чувство и раньше никто так не делал.
Jaccard index или Neighbourhood overlapping
В основе алгоритма Core Expansion лежит показатель, который авторы почему-то назвали Neighbourhood overlapping, хотя, по моему мнению, это просто несколько модифицированный Jaccard Index. Для двух любых связанных вершин графа это, по сути, количество их общих соседей, поделенное на их общее количество всех соседей. Используя этот показатель, авторы переходят от невзвешенного графа к взвешенному, где вес каждого ребра – это Jaccard index вершин на концах этого ребра (или Neighbourhood overlapping по терминологии авторов).
static class processEdgeTask implements Runnable {
private final FastutilMapIntVertexGraph<DefaultWeightedEdge> graph;
private final DefaultWeightedEdge e;
private final Map<Integer, IntHashSet> cache;
private final int bigNNThreshold;
public processEdgeTask(
FastutilMapIntVertexGraph<DefaultWeightedEdge> graph,
DefaultWeightedEdge e,
Map<Integer, IntHashSet> cache,
int bigNNThreshold
) {
this.graph = graph;
this.e = e;
this.cache = cache;
this.bigNNThreshold = bigNNThreshold;
}
@Override
public void run() {
int src = graph.getEdgeSource(e);
int dst = graph.getEdgeTarget(e);
IntHashSet srcNN, dstNN;
if (cache.containsKey(src)) {
srcNN = cache.get(src);
} else {
srcNN = NeighbourhoodFinder.find(graph, src);
if (srcNN.size() >= bigNNThreshold) {
cache.put(src, srcNN);
}
}
if (cache.containsKey(dst)) {
dstNN = cache.get(dst);
} else {
dstNN = NeighbourhoodFinder.find(graph, dst);
if (dstNN.size() >= bigNNThreshold) {
cache.put(dst, dstNN);
}
}
double w = (srcNN.count(dstNN::contains) * 1.0);
IntHashSet union;
if (srcNN.size() > dstNN.size()) {
union = new IntHashSet(srcNN);
union.addAll(dstNN);
} else {
union = new IntHashSet(dstNN);
union.addAll(srcNN);
}
if (union.size() > 2) {
w /= (union.size() - 2);
} else {
w = 0.0;
}
graph.setEdgeWeight(e, w);
}
}Выделение "ядер"
Процесс выделения "ядер" будущих сообществ тоже простой. Мы для каждой вершины считаем ее взвешенную степень – сумму весов всех связанных с вершиной ребер. Дальше ядрами считаем те вершины, которые являются локальными максимумами среди всех своих соседей. Если среди соседей нашлось несколько максимумов, то их помещаем в одно ядро.
class CoresFinder {
public <V, E> IntObjectHashMap<IntHashSet> find(ExtendedGraph<V, E> graph) {
Set<Integer> vertices = graph.getFastutilGraph().vertexSet();
IntHashSet visited = new IntHashSet(vertices.size());
IntObjectHashMap<IntHashSet> cores = new IntObjectHashMap<>();
for (int v : vertices) {
applyAdditionalCores(v, graph.getVertexWeights(), visited, cores, graph.getFastutilGraph());
}
return cores;
}
private void applyAdditionalCores(
int v, IntDoubleHashMap vertexWeights,
IntHashSet visited, IntObjectHashMap<IntHashSet> cores,
FastutilMapIntVertexGraph<DefaultWeightedEdge> g) {
double vW = vertexWeights.get(v);
if (Double.compare(vW, .0) == 0) {
return;
}
IntHashSet nn = NeighbourhoodFinder.find(g, v);
IntHashSet coreVertices = new IntHashSet();
coreVertices.add(v);
if (nn.size() == 0) {
visited.add(v);
cores.put(v, coreVertices);
return;
}
IntHashSet equalsWeightsNodes = new IntHashSet();
IntIterator iter = nn.intIterator();
int n;
while (iter.hasNext())
{
n = iter.next();
if (vertexWeights.get(n) > vW) {
visited.add(v);
return;
}
if (Double.compare(vertexWeights.get(n), vW) == 0) {
equalsWeightsNodes.add(n);
}
}
equalsWeightsNodes.forEach(
candidate -> {
if (visited.contains(candidate)) {
visited.add(v);
return;
}
coreVertices.add(candidate);
}
);
cores.put(v, coreVertices);
visited.add(v);
}
}"Расширение" ядер
После того, как все ядра найдены, мы начинаем их расширять. Для каждой, еще не проклассифицированной вершины, мы ищем ближайшее к ней ядро. Ядро считается ближайшем, если сумма весов ребер из нашей вершины в вершины, принадлежащие данному ядру, максимальная среди всех потенциальных ядер-кандидатов. Найдя такой максимум, мы помещаем вершину в это ядро, то есть сообщество. Если же максимума нет или он равен нулю, то вершина остается неклассифицированной. Повторяем процесс до тех пор, пока либо не кончатся неклассифицированные вершины, либо не кончатся варианты как их классифицировать. Алгоритм оставляет возможность вершине быть без сообщества. Это не баг, а скорее, фича, но ее надо обязательно учитывать.
static class findCoreTask implements Runnable {
private final FastutilMapIntVertexGraph<DefaultWeightedEdge> g;
private final IntIntHashMap cores;
private final int v;
private final IntIntHashMap results;
findCoreTask(
IntIntHashMap cores, Integer v,
FastutilMapIntVertexGraph<DefaultWeightedEdge> g,
IntIntHashMap results
) {
this.g = g;
this.v = v;
this.cores = cores;
this.results = results;
}
@Override
public void run() {
IntDoubleHashMap candidates = new IntDoubleHashMap();
g.edgesOf(v).forEach(e -> {
int n;
if (g.getEdgeSource(e).equals(v)) {
n = g.getEdgeTarget(e);
} else {
n = g.getEdgeSource(e);
}
int neighbourComm = cores.get(n);
if (neighbourComm != -1) {
candidates.put(
neighbourComm,
candidates.getIfAbsent(neighbourComm, 0.0) + g.getEdgeWeight(e)
);
}
});
int closestCore = -1;
double maxWeight = Double.NEGATIVE_INFINITY;
int cnt = 1;
for (IntDoublePair candidate : candidates.keyValuesView()) {
if (candidate.getTwo() > maxWeight) {
maxWeight = candidate.getTwo();
closestCore = candidate.getOne();
cnt = 1;
} else if (Double.compare(candidate.getTwo(), maxWeight) == 0) {
cnt++;
}
}
if (cnt == 1) {
results.put(v, closestCore);
} else {
results.put(v, -1); // Vertex is left unclassified until the next iteration.
}
}
}Результаты из статьи
Авторы оценивают сложность алгоритма следующим образом: , где N –число вершин, а M – число ребер. Также они приводят результаты кластеризации с картинками в сравнении с Louvain и Girvan-Newman для графов средних размеров.
Например, так выглядят выделенные данным алгоритмом сообщества в графе Facebook (картинка из оригинальной работы, ссылка и библиография в шапке):

Количество выделенных сообществ
| Network | Girvan-Newman | Louvain | Core expansion |
|---|---|---|---|
| Zachary | 5 | 4 | 2 |
| Dolphins | 5 | 5 | 4 |
| Les Miserable | 11 | 6 | 3 |
| Polbooks | 5 | 4 | 2 |
| не отработал | 16 | 9 |
Видно, что с помощью алгоритма Core expansion выявляется меньше сообществ. Причиной этому может быть возможность оставить вершину без сообществ.
Граф Facebook (от Stanford Large Network Dataset Collectoion), содержащий 4к вершин и 90к ребер, для алгоритма Girvan-Newman оказался слишком толстым. Возможно, у авторов не было возможности ждать десятки часов, пока о�� завершится. Справедливости ради следует отметить, что существуют эвристики и модификации алгоритма Girvan-Newman, которые позволяют его немного ускорить, но решительно ничего не меняют (графы с десятками тысяч вершин являются для них пределом).
Для некоторых графов в научном сообществе существует консенсус по поводу истинных сообществ. Core Expansion их точно находит, по крайней мере, для небольшого графа Les Miserable (картинка из оригинальной работы, ссылка и библиография в шапке):
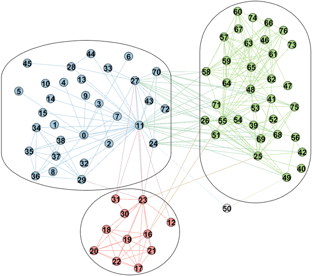
Modularity score
Так как Core Expansion не оптимизирует Modularity напрямую, то по этой метрике он проигрывает жадным алгоритмам, но это ни плохо, ни хорошо, а просто закономерно:
| Network | Girvan-Newman | Louvain | Core expansion |
|---|---|---|---|
| Zachary | 0.4013 | 0.416 | 0.371 |
| Dolphins | 0.5193 | 0.5193 | 0.512 |
| Les Miserable | 0.538 | 0.549 | 0.415 |
| Polbooks | 0.5168 | 0.525 | 0.448 |
| не отработал | 0.835 | 0.731 |
Наоборот, я бы отметил, что итоговый показатель Modularity очень даже неплох для алгоритма, который не оптимизирует этот показатель явно.
Большие графы и NMI
Авторы также натравили свой алгоритм на два графа, которые они назвали большими – DBLP (317к вершин, 1.05кк ребер) и Amazon (335к вершин, 925к ребер), – и сравнили их с Louvain, но теперь по двум метрикам – Modularity и Normalized Mutual Information. Последнюю метрику обычно применяют для оценки алгоритмов выделения перекрывающихся сообществ, но оставим это на совести авторов.
По Modularity Louvain, очевидно, победил, а по NMI проиграл просто в силу своей жадной природы. Core Expansion в этом смысле оказался более "сбалансированным":
| Network | Louvain NMI | Louvain Modularity | CE NMI | CE Modularity |
|---|---|---|---|---|
| DBLP | 0.25 | 0.82 | 0.48 | 0.683 |
| Amazon | 0.38 | 0.926 | 0.55 | 0.754 |
Сообщества в случайных графах
На мой взгляд, одно из самых интересных наблюдений авторов и одно из главных преимуществ Core Expansion – это выявление сообществ в случайных графах. Авторы сгенерировали случайные графы. Они похожи на Erdos-Renyi, где ребра просто выбираются случайно с заданной вероятностью, которая потом определяет плотность графа. По логике в таких графах сообществ нет, или почти нет. Жадные алгоритмы при этом сообщества находят (опять же, в силу своей природы), а вот Core Expansion – почти нет. Это позволяет говорить о некоторого рода "устойчивости" этого алгоритма к шуму.
Ниже сравнение алгоритмов по количеству выявленных сообществ в случайных графах:
| Network | Girvan-Newman | Louvain | Core expansion |
|---|---|---|---|
| 50 вершин, density 0.2 | 28 | 4 | 1 |
| 50 вершин, density 0.4 | 23 | 4 | 1 |
| 100 вершин, density 0.2 | 67 | 7 | 1 |
| 100 вершин, density 0.4 | 62 | 5 | 1 |
| 200 вершин, density 0.2 | 112 | 7 | 2 |
| 200 вершин, density 0.4 | 116 | 6 | 2 |
Наша реализация алгоритма Core expansion на Java
Как и у многих научных статей, у этой есть стандартная проблема – в ней нет кода реализации алгоритма, и мы не можем ни воспроизвести результаты, ни попробовать этот алгоритм на своих задачах.
Мы решили устранить этот недостаток и написали свою реализацию алгоритма Core expansion на Java, которая доступна в GitHub под MIT-лицензией.
Может возникнуть вопрос, почему Java? Обычно к статьям идет код на C++, а Data Scientist-ы, которые работают с машинным обучением на графах, привыкли к Python. Ответ прост и включает в себя несколько моментов:
- Разработка на Java значительно быстрее, чем на C++, к тому же в нашем банке это один из основных языков.
- Графовые библиотеки для Python (snap, graph-tool, networkit, etc.) обычно работают быстро, когда запускаешь что-то уже реализованное в самой библиотеке (потому что готовые алгоритмы написаны там на чистом C++), но когда начинаешь писать что-то свое, то упираешься в GIL и медленные циклы Python.
Для нас Java является удобным компромиссом, позволяющим и быстро написать масштабируемый production код, и реализовать последние достижения в области Network Science, описанные в научных работах.
JGraphT
Для Java существует несколько библиотек, которые содержат основные структуры и алгоритмы из теории графов. Одна из них JGraphT, распространяющаяся под Eclipse-лицензией. Эта библиотека, несмотря на свой солидный возраст (версия 0.4.0 вышла аж в 2003-м году), активно развивается (не так давно как раз был релиз новой версии 1.4.0).
Большой возраст, активное комьюнити, высокая стабильность, богатое API и много реализованных базовых алгоритмов делают эту библиотеку идеальным для нас кандидатом для построения, как ETL-пайплайнов обработки графов, так и backend-а, в котором необходимо производить вычисления на лету и применять графовые алгоритмы.
Но стоит отметить, что применительно к данной статье использование библиотеки такого уровня не нужно, но единообразие удобно, особенно если выделение сообществ лишь часть большого пайплайна обработки данных.
Многопоточность и оптимизация производительности
Большим преимуществом авторского алгоритма в сравнении, например, с Louvain является то, что все операции можно выполнять независимо. Напрашивается параллелизация вычислений, что мы и сделали. Вычисление Jaccard Index выполняется параллельно для всех ребер. Также параллельно для всех вершин выполняется подсчет их весов и поиск ближайшего ядра для неклассифицированных вершин. Это дало существенный прирост производительности в сравнении с наивной реализацией. В итоге наша реализация вполне эффективно обрабатывает графы с миллионами вершин и ребер даже на простом домашнем ноутбуке (за порядка 100-300 сек, в зависимости от машины).
По ощущениям этот алгоритм оказывается даже быстрее, чем Louvain, который мы также реализовали самостоятельно, но детальных бенчмарков пока не делали. Так как логика вычислений совсем простая, то мы обошлись встроенной в JDK парадигмой пулов потоков и синхронизируемых ресурсов типа ConcurrentHashMap.
Проводя тесты с относительно большими графами, мы заметили, что самой "тяжелой" частью алгоритма является вычисление Jaccard Index для ребер, и проблема производительности сильно усугубляется с ростом размера графа. Предположив, что это связано с тяжелым хвостом экспоненциального распределения количества вершин со степенью k от самого k, мы нашли частичное решение.
Кэширование множества соседей для самых "толстых" вершин графа дало хороший прирост в производительности. В итоге внутри кода есть магические эвристики (например, кэшируем лишь вершины, связанные более чем с 10% всего графа), но мы писали это практически "за выходные", так что as is.
Коллекции Eclipse
Если мы пронумеруем вершины исходного графа, как числа Integer и такой же тип будем использовать для нумерации сообществ, то большая часть операций сведется к обращениям к хеш-таблицам вида Map<Integer, Integer> или нахождению пересечений и объединений множеств чисел типа Set<Integer>.
Как следствие, сразу появилась мысль попробовать Eclipse Collections, до которых раньше не доходили руки. Эти коллекции предоставляют более быстрые имплементации коллекций примитивов: IntIntHashMap и IntHashSet, на которых и построена большая часть нашей реализации.
Тесты и производительность
Результаты из статьи
Для начала мы написали тесты, проверяющие небольшие графы из статьи. Результаты в точности совпали с теми результатами, описанные авторами.
Для графа Poolbooks мы сделали отдельный тест. Он запускается 1000 раз, чтобы убедиться, что алгоритм полностью детерминирован и не зависит от того, в каком порядке выполнять итерации по вершинам (это неприятное свойство Louvain алгоритма).
Для графов побольше мы проверяли лишь совпадение числа сообществ с тем, которое было у авторов статьи. Все совпало. Результаты авторов воспроизводятся без проблем и сам алгоритм описан полностью корректно. Тесты лежат там же, на GitHub.
Тесты для большого графа
Мы решили провести более интересные, чем у авторов статьи тесты, взяв граф побольше. Мы выбрали граф Youtube из Стэнфордской коллекции графов. Он содержит почти 3кк ребер, соединяющих 1.1кк вершин, являясь при этом полностью связным. Для данного графа известны ground truth сообщества, которых в нем насчитывается порядка 8.5 тысяч.
Производительность
На моей машине с AMD A12 9720P и Java 11 без каких-либо дополнительных флагов, вычисления занимают ~290 секунд. У коллег с Intel Core i7 процесс почти в два раза быстрее. Детальных бенчмарков мы не проводили, но масштаб, думаю, понятен. Тестировать на графах большего размера мы не стали, так как начинаются проблемы с оперативной памятью в обычных ноутбуках, а сервера под рукой у нас не было.
Субъективно, несмотря на бОльшую формальную сложность в сравнении с Louvain, Core Expansion хорошо масштабируется за счет распараллеливания и может быть применен для действительно больших графов на сервере с каким-нибудь 12-и ядерным Xeon и большим количеством оперативной памяти.
Выделенные сообщества
Core Expansion выделил в графе YouTube порядка 19к сообществ. Однако 3.5к из них были сообществами из одной вершины и еще 4к сообществами из двух вершин. Если их отбросить, то результаты уже не кажутся плохими. Для подобного плотного и сложного графа 11.5к сообществ при 8.5 ground truth выглядят нормально.
Заключение
У многих наверное возник вопрос, откуда в банке берутся графы? Поэтому расскажу немного о нашей команде и о том, чем мы занимаемся.
Наша команда в Райффайзенбанке занимается тем, что сегодня называется Organizational Network Analysis – мы представляем организацию, как сеть или граф взаимодействующих сущностей (наподобие социальной сети). Сущности могут быть различными, начиная от офисов или дирекций, заканчивая Agile-командами и отдельными сотрудниками. Взаимодействия между сущностями также могут быть самыми разнообразными, например, постановка задач в системах типа Jira, комментарии в Confluence, активности в BitBucket, встречи и т.д.
В итоге мы получаем Multilayer Temporal Mixed Network – максимально сложный и интересный объект, техники работы с которым в наши дни очень активно развиваются. Сейчас наша команда работает на самом переднем крае развития Network Science, а имплементация научных статей из последних журналов для нас это, можно сказать, повседневная работа.
Надеемся, мы еще расскажем более подробно о наших задачах и кейсах в дальнейшем. Также будем рады любым замечаниям и предложениям по нашей имплементации статьи о Core Expansion. Как говорится, Welcome to contribute! Спасибо за внимание!

