
Прочие статьи цикла
AES — американский стандарт шифрования. Часть I
АES — американский стандарт шифрования. Часть II
AES — американский стандарт шифрования. Часть III
AES — американский стандарт шифрования. Часть IV
AES — американский стандарт шифрования. Часть V. Атака
АES — американский стандарт шифрования. Часть II
AES — американский стандарт шифрования. Часть III
AES — американский стандарт шифрования. Часть IV
AES — американский стандарт шифрования. Часть V. Атака
В этой IV части завершаем описание шифра АЕS — 128. Для читателей не знакомых с предшествующими частями работы поясню, что материал излагается в учебных целях и это накладывает ряд особенностей (детализация, числовые примеры, математические основы и др.) Предполагается не просто ознакомление со стандартом, а использование излагаемого материала для разработки алгоритмов зашифрования и дешифрования (при отсутствии ключа). Авторы множества известных в сети (и вне её) публикаций не ставили перед собой таких целей, что делает эти публикации малопригодными для наших целей.
Процесс обратный зашифрованию называется расшифрованием сообщений. Для расшифрования (с ключом) шифрованных текстов (ШТ) создается инверсная таблица замен и раундовые ключи, которые используются в обратном порядке относительно схемы для шифрования, но подобно процессу зашифрования.
Расшифрование сообщений AES
Перечень операций при расшифровании сообщения остается таким же как и при зашифровании. Подробнее с операциями можно ознакомиться здесь. Это достаточно общий принцип шифров — единая аппаратная реализация при шифровании и расшифровании, что обеспечивается наборами одинаковых функций для обоих процессов. Меняется лишь исходный текст и последовательность подачи на вход ключей.
Процесс расшифрования сообщений реализуется как последовательность обратных (инверсных) преобразований, используемых при шифровании, в порядке обратном их следованию при зашифровании. Очевидно также, что раундовые ключи используются в соответствующей последовательности: вначале ключ, полученный последним, затем предпоследний и так далее до первого раундового ключа.
Названия всех преобразований остаются теми же, но получают префикс Inv. Будем рассматривать их в той же последовательности, что и ранее. Шифр AES допускает два варианта расшифрования обратного и прямого, что подробно рассматривается далее.
Вариант обратного расшифрования
Обратное расшифрования сообщения — естественный процесс обращающий вспять процесс зашифрования.
Операция AddRoundKey остается как и при зашифровании сообщения такой же (без изменения) S + Ki для всех 16 байтов состояния State, т.е. является обратной самой себе. Это объясняется тем, что используется в операции логика XOR, а байты представимы двоичными числами.
К шифрованному сообщению просто добавляется (суммируется) ключ последнего раунда.
InvSubBytes. Сущность этого преобразования не изменилась, т. е. каждый байт преобразуемого сообщения заменяется другим, взятым из таблицы (S-1-блока) замены. Конечно, таблица замен здесь используется другая. Байт {x, y} заменяется байтом из Inv S (x, y) по такому же принципу: х – строка таблицы, у – ее столбец. Заменяющий байт извлекается из ячейки на пересечении строки (х) и столбца (у) таблицы Inv S(x, y).
Как и ранее, размер таблицы 16×16 = 256 байтов, каждый из которых получен путем векторно-матричного умножения и вычитания (аффинного преобразования) из произведения вектора сдвига С. В двоичных полях операции сложения и вычитания эквивалентны, поэтому вектор С можно просто прибавлять к произведению. Вид таблицы InvSubBytes приводится ниже. Указанный узел замен S-1 представлен в следующей таблице 1, значения приведены в 16-ричном формате:
Таблица 1. Таблица замен инверсного S-1 — блока

В таблице показаны примеры замен двух байтов 4А → 5С и 9F→6Е заливка зеленым цветом.
InvShiftRows. Данное преобразование осуществляет сдвиг строк в таблице (квадрате State) вправо (в направлении, противоположном исходному сдвигу). Значение величины сдвига для каждой строки остается прежним: первая (верхняя) строка не сдвигается c0 = 0, вторая — сдвигается на c1 = 1, следующая – на c2=2 и последняя – на c3=3 позиции (клетки). Значения c0, c1,c2 ,c3 приводились в таблице и на рисунке ранее для первого раунда преобразования сообщения.

Результат такого умножения в скалярном представлении получает вид:
S’0C = ({0l} ·S0C) ⊕ ({0b}·S1C) ⊕ ({0d}·S2C) ⊕ ({09 }·S3C);
S’1C = ({09}·S0C) ⊕ ({0l}· S1C) ⊕ ({0b}·S2C) ⊕ ({0d }·S3C);
S’2C = ({0d}·S0C) ⊕ ({09}·S1C) ⊕ ({0l}· S2C) ⊕ ({0b }·S3C);
S’3C = ({0b}·S0C) ⊕ ({0d}·S1C) ⊕ ({09}·S2C) ⊕ ({ 0l }·S3C).
Для получения ИТ из ШТ алгоритм расшифрования использует те же значения параметров, которые использовались в процессе шифрования. Для формирования развернутого ключа правила остаются прежними.
Вариант прямого расшифрования
Особенности алгоритма расшифрования для некоторых обратных преобразований позволяют сохранить тот же порядок следования операций, что и в алгоритме шифрования, но при этом часть значений параметров требует изменений. Речь, прежде всего, идет о ключе (его разворачивании).
Исследования показали, что порядок следования функций SubBytes ( ) и ShiftRows ( ) не меняет значения результата, т. е. эти функции перестановочны (они коммутируют). Это положение (свойство) справедливо и для функций InvSubBytes ( ), InvShiftRows ( ). Эта закономерность легко объяснима. Дело в том, что обе функции оперируют с целыми байтами, а сдвиги выполняются на целое число, кратное байту, и не изменяют значения самих байтов.
Относительно операции MixColumns ( ) заметим следующее. Она является линейной по отношению к входным байтам (к данным).
InvMixColumns (State XOR Round Key) = InvMixColumns (State)XOR
InvMixColumns (Round Key).
Эти особенности функций (свойства) допускают изменение порядка их применения, т. е.
InvSubBytes (InvShiftRows ( )) = InvShiftRows (InvSubBytes ( )).
AddRoundKey (InvMixColumns ( )) = InvMixColumns (AddRoundKey ( )),
но при условии, что столбцы (32-разрядные слова) развернутого ключа расшифрования предварительно пропущены через функцию
InvMixColumns ().
Изложенное означает, что путь расшифрования ШТ может быть сделан эффективным за счет сохранения порядка использования функций, принятого для шифрования. Очевидно, что в этом случае затраты на аппаратную и программную реализацию шифра существенно сокращаются. Изменения касаются только процедуры формирования развертывания ключа.
В функции InvMixColumns ( ) необходимо выполнять преобразование типа переменной, входной параметр функции – двумерный массив байтов (квадрат), а развернутый ключ формируется как линейный (строка) массив 32-разрядных слов. По этой причине необходимо выполнить согласование типов до квадрата.
Покажем на примере 2-раундового преобразования два эквивалентных варианта процедуры расшифрования RIJNDAEL. Первый вариант – обычная инверсия функции шифрования. Второй вариант получается из первого путем изменения порядка следования операций в трех парах преобразований
InvShi ftRows ( ) → InvSubBytes ( ) 2 раза и
AddRoundKey ( ) → InvMixColumns ( ) 1 раз.
Результат преобразования сохраняется при переходе от исходной к обратной
последовательности выполнения операций в указанных парах.
Из таблицы видим, что процедура шифрования и второй вариант процедуры расшифрования совпадают с точностью до порядка использования раундовых ключей (при выполнении операций AddRoundKey), таблиц замен (при выполнении операций SubBytes () и InvSubBytes ()) и матриц преобразований (при выполнении операций MixColumns ( ) и InvMixColumns ( )).
Таблица 2 – Последовательность преобразований в двухраундовом варианте RIJNDAEL

Подобный результат оказывается справедливым для любого числа раундов.
Восстановление ключа шифра с использованием последнего подключа
Выработка раундовых ключей шифра AES. Процедура (Key Schedule) выработки раундовых ключей из 128-разрядного исходного ключа шифра представляет собой рекурсивную функцию. Эта функция подробным образом рассмотрена здесь. Начальными условиями для ее запуска являются 4 первых 4-х байтовых слова ключа (4×32 – разрядные слова), т. е. W[0], W[1], W[2], W[3]. Сформулируем задачу восстановления этого 128-разрядного ключа шифра следующим образом:
Пусть найдены компоненты раундового ключа 10 раунда W[43], W[42], W[41], W[40].
Требуется восстановить полный ключ шифра, располагая только этим раундовым ключом.
Удобно рассмотреть решение задачи вначале на числовых данных. За основу возьмем числовой пример, приведенный в работе FIPS PUB 197. Таблица 3 содержит ключ 10 раунда.
Процедура выработки раундовых ключей организована так, что она обеспечивает движение вперед (разворачивание ключа) по ряду предшествующих значений ключа. Для движения вспять из некоторой точки ряда значений необходимо располагать исходными данными процесса вычислений в этой точке возврата. Пусть точкой возврата будет последний шаг последнего 10 раунда, т. е. известны четыре 4-х байтовые слова ключа 10 раунда Nk = Nb = 4.
Таблица 3 – 128-разрядный ключ 10 раунда шифра AES

Далее результаты и действия алгоритма восстановления ключа помещены для удобства в таблицу 4, подобную (как бы опрокинутую) таблице формирования ключа.
Таблица 4 – Восстановление ключа шифра по известному ключу 10-го раунда

Пояснения к таблице 4. Отсчет номеров раундов следует в обратном порядке от 10-го к 1-му. В трех колонках (3, 8, 9) таблицы содержатся готовые ключи с различными текущими номерами, зависящими от номера i строки. В остальных клетках помещаются вспомогательные данные промежуточных вычислений. Таким образом, значение ключа W[i] появляется в таблице три раза в трех колонках.
Колонки 1 и 2 – это номер r раунда и порядковый номер i 4-х байтового слова ключа. Последнее такое слово при шифровании имеет номер i = 43. В таблице его записываем в верхней строке правой (9) колонки. Номера i строк таблицы убывают и им в графе 9 соответствуют слова ключа W[i]. В 8-й колонке помещается слово W [i – Nk] ключа с уменьшенным номером W [43 – 4] = W[39], а в 3-ей колонке – слово ключа W[i – 1] = W[42], предшествующее W[i] = W[43].
Значение слова W[39] в 8-й колонке неизвестно и его находим по исходным данным с использованием формулы:
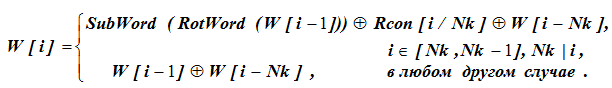
Для вычислений по формуле вначале выполняется проверка условий выбора строки формулы. Для W[43], i = 43 и Nk не делит нацело значение 43, т. е. для i = 43 значение W[i] определяется по нижней строке формулы: W[43] = W[42] W[39]. Здесь при заданных значениях W[42] и W[43] не определено последнее слагаемое W[39].
Тогда W[39] = W[43] W[42] = b6630ca6 — e13f0cc8.
В двоичной арифметике по mod2 операции сложения и вычитания равносильны, поэтому поразрядные вычисления для каждого из 4-х байтов ключевого слова W[39] приобретают вид (табл. 5):
Таблица 5 – Побайтные вычисления ключевого слова W[39].

Таким образом, найдено значение ключевого слова W[39] = 575c006e. Это значение переносим в 3-ю колонку, в строку i = 40 и в 9 колонку в строку i = 39.
Вычисления в строке i = 40 проводятся как при расширении ключа.
Неизвестное слово W[i – Nk] = W[40 –Nk] = W[i =36] должно определяться как в предыдущем случае разностью W[36] = W[40] 7 колонка строки 40.
В свою очередь значение в 7-й колонке строки 40 формируется как сумма (ХОR) 5-й и 6-й колонок. Значение 5-й колонки получается из W[39] после циклического сдвига RotWord (4-я колонка) и операции замены SubWord (5-я колонка).
Результаты этих действий приобретают вид
RotWord (575c006e) = 5c006e57; SubWord (5c006e57) = 4a639f5b.
Значение в 6-й колонке получается, как константа
Rcon [j = i/Nk]= Rcon [j = 40/4] = 2 j-1 = 29.
Эта константа представляется байтом в 16-ричном виде
29 ≈100000000=х9, но в поле GF(28) такого байта нет: необходимо найти остаток от деления на неприводимый многочлен, т. е.
После включения константы в ключевое слово имеем
Rcon [j=40/Nk]=36000000 (6-я колонка). Значение 7-й колонки получаем в виде (7 колонка)=(5 колонка)⊕(6 колонка)=4a639f5b⊕36000000=7c639f5b.
И окончательно для
W [36] = W[40] (7-я колонка строки 40) = d014f9a8 7c639f5b = ac7766f3.
Дальнейшие вычисления по аналогии приводят к окончательному результату — ключу шифра.
Имеется дополнительная информация относительно w и RotWord, функций Rcon и SubWord. Допустим, что обозначили через Kr [j] – j-ый байт r-го раундового ключа и w[i] как в документации.
Получаем: Kr = (w[Nk ∙ r], w[Nk∙ r + 1], · · ·, w[Nk ∙r + Nk − 1]).
Для разных i имеем следующие отношения
для i≠0 mod Nk, Nk ≤ i < Nb∙ (Nr +1), w[i] = w[i – Nk] xor w[i – 1] и
для i=0 mod Nk, w[i] = w[i – Nk] xor SubWord(RotWord(w[i–1]))xorRcon[i/ Nk].
Следовательно, имеем для i≠0modNk, Nk 0≤i < Nb∙(Nr+1)–Nk, w[i]=w[i+Nk] xor w[i + Nk – 1] и для i=0modNk, w[i]=w[i+Nk]xorSubWord(RotWord(w[i+Nk–1]))xorRcon[i+Nk/Nk]
С AES-256, необходимо добавить операцию Subword, когда i сравнимо с 4mod Nк. Так что возможно выводить предыдущий ключ из заключительного подключа и шаг за шагом получаем значение K0 шифрключа.
Математические основы шифра AES — 128 достаточно полно и подробно изложены здесь.
Обратимся к отображению поля ℓ: GF (28) → GF (28); x→x2 + x. Образ этого отображения
Е1 = Im(l) имеет размерность dim GF(2) (Е1) = 7.
Уравнение x2 + x = θ, где θ Е1 имеет два различных решения (корня уравнения) х1, х2є GF (28).
По теореме Виета х1⊕х2 = 1 сумма корней равна коэффициенту уравнения при х2 с противоположным знаком, а произведение корней х1⊗х2 = θ равно свободному члену уравнения (в нашем уравнении с противоположным знаком).
Известно, что в арифметике двоичных полей операции суммирования и вычитания элементов по mod2 эквивалентны.

Таким образом, корни уравнения связаны соотношением х2 = х1⊕1, так как коэффициент при х в уравнении равен 1. Это означает, что в десятичном представлении элементов поля при лексикографическом их упорядочении они располагаются один за другим, отличаясь лишь на единицу.
Так при х = 0 и х = 1 и при х = 2 и х = 3 получаем:

Результаты (образы) отображения в приведенных парах (0, 1); (2, 3) полностью совпали, т.е. два прообраза соответствуют одному образу. Следовательно, мощность образа в два раза меньше мощности прообраза и его размерность его элементов равна 7.
Произведение пар корней, т. е. свободный член квадратного уравнения удобно определить через степенное представление элементов поля (прообразов). Показатели степеней при этом суммируются по mod255, т.е. по модулю порядка мультипликативной группы поля GF (28).






