За основу задания динамических свойств систем может быть принята любая из форм представления операторов: дифференциальные уравнения (ДУ), передаточные функции (ПФ), временные характеристики (ВХ) или частотные характеристики (ЧХ), однако для конкретных задач целесообразно выбирать наиболее рациональную форму [1].
Возможные преобразования форм представления моделей вход-выход показаны на Рисунок 1. Сплошные линии орграфа показывают однозначные преобразования, штриховые - неоднозначные преобразования экспериментальных данных. Результаты последних преобразований зависят от выбора структуры оператора и алгоритма обработки данных.
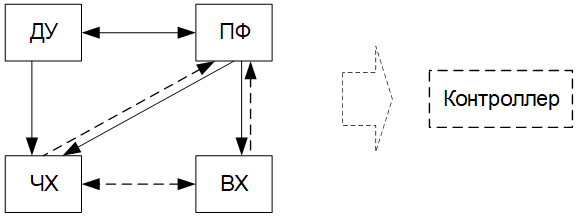
Рисунок 1. Орграф взаимосвязи форм представления моделей. Модели могут описывать поведение регуляторов систем управления [4], наблюдателей [3], корректирующих звеньев, фильтров [5], и др. динамических систем. В этой работе рассматриваются MATLAB преобразования форм представления моделей и реализация моделей средствами контроллеров.
Дискретная модель объекта
Для сравнения результатов преобразования моделей будем использовать одну и ту же систему - объект третьего порядка, дискретная модель которого в форме пространства состояний имеет следующие коэффициенты.
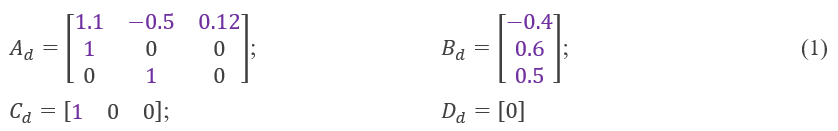
Дискретная модель в форме пространства состояний представляется разностными уравнениями первого порядка

Связь переменных уравнений (2) показана на блок схеме Рисунок 2, где X – переменные состояния; 1/z – задержка на один такт.
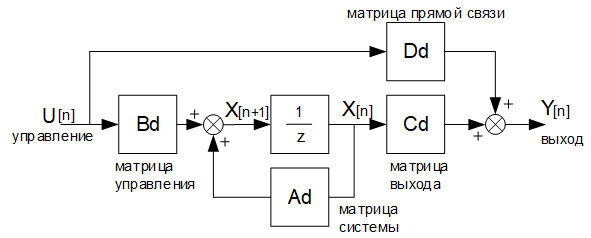
Рисунок 2. Структура дискретной модели объекта в форме пространства состояний.
Система разностных уравнений
Раскроем уравнения (2) подстановкой в уравнения матриц (1) объекта:
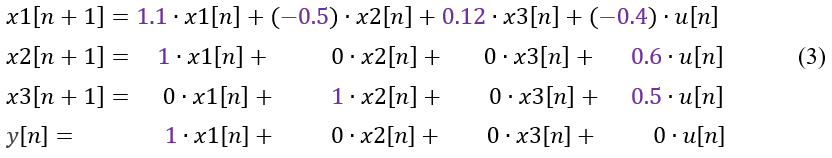
По разностным уравнениям (3) построим Simulink модель дискретного объекта с периодом дискретизации 1 с (см. Рисунок 3).
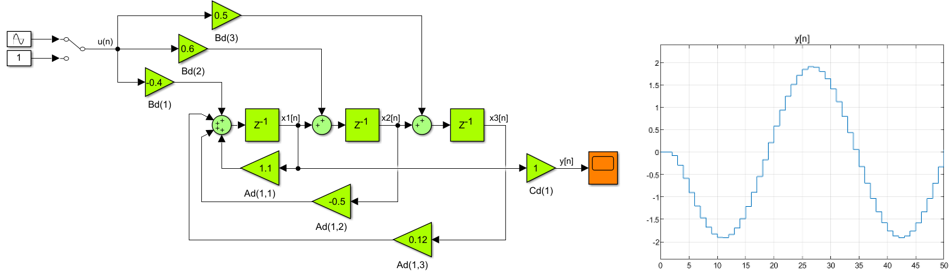
Рисунок 3. Дискретная модель объекта (1) и реакция y[n] объекта на синусоидальное u[n] воздействие.
Импульсная передаточная функция
Воспользуемся преобразованием форм MATLAB для перевода дискретной модели из пространства состояний в формат импульсной передаточной функции, затем в формат непрерывной ПФ и, наконец, в формат пространства состояний непрерывной модели. Ниже показан код m-программы c промежуточными результатами, сдвинутыми вправо на 1 Tab.
Ad = [1.1 -0.5 0.12
1.0 0.0 0.0
0.0 1.0 0.0];
Bd = [-0.4
0.6
0.5];
Cd = [1 0 0];
Dd = 0;
Wo_ss_d = ss(Ad,Bd,Cd,Dd,1); % структура дискретной модели с периодом 1 с
Wo_tf_d = tf(Wo_ss_d) % дискретная ПФ

Непрерывная передаточная функция
Wo_tf_c = d2c(Wo_tf_d) % непрерывная ПФ

Непрерывная модель в форме пространства состояний
Wo_ss_c = ss(Wo_tf_c) % непрерывная модель в форме пространства состояний
Wo_ss_c =
A =
x1 x2 x3 (4)
x1 -2.12 -1.213 -0.819
x2 2 0 0
x3 0 0.5 0
B =
u1
x1 2
x2 0
x3 0
C =
x1 x2 x3
y1 0.009016 -0.2697 -0.8307
D =
u1
y1 0
Continuous-time state-space model.
ВНИМАНИЕ. Изменение шага дискретизации приводит к соответствующему изменению динамики модели. Для того, чтобы эквивалентная непрерывная модель “не отставала” и “не убегала” от дискретной модели с новым шагом дискретизации, необходимо пересчитать коэффициенты непрерывной модели.
Приведенный многоступенчатый перевод дискретной модели (1, 2, 3) в непрерывную модель пространства состояний (4) можно выполнить одной командой d2c: Wo_ss_c = d2c(Wo_ss_d). В этом варианте получится набор матриц с другими коэффициентами относительно многоступенчатого варианта, но это не является ошибкой, поскольку одна и та же ПФ (с одинаковым составом нулей и полюсов) может быть представлена в форме пространства состояний разными вариантами коэффициентов матриц A, B, C, D. Нули и полюса ПФ можно вычислить командами MATLAB: zeros, poles, eig.
Система дифференциальных уравнений
Матрицы (4) непрерывной модели связывают переменные состояния x(t) с входом y(t) и выходом u(t) модели следующим образом.

Раскроем систему дифференциальных уравнений (5) подстановкой коэффициентов матриц (4):
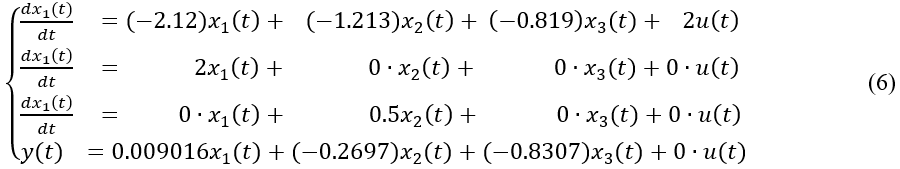
Как в случае построения дискретной Simulink модели (Рисунок 3) по разностным уравнениям (3), построим Simulink модель непрерывного объекта (см. Рисунок 4) по дифференциальным уравнениям (6).
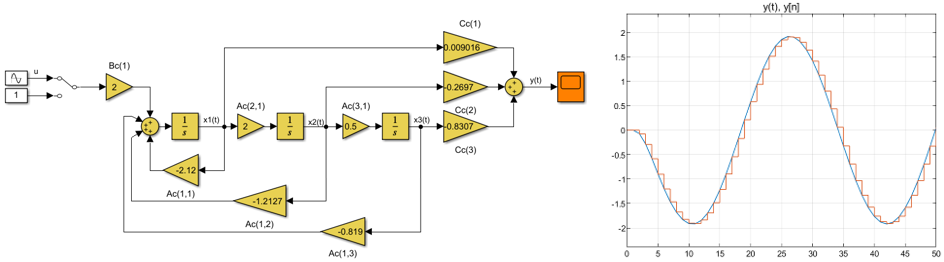
Рисунок 4. Непрерывная модель объекта (1) и реакция y(t) объекта на синусоидальное u(t) воздействие (синий график). Для сравнения, показан коричневый график y[n] дискретного объекта Рисунок 3, график y(t) сдвинут вправо на 0.5 с - половину дискреты.
Перевод модели в частотную область
В MATLAB по данным модели пространства состояний или передаточным функциям можно построить соответствующие амплитудно-фазовые частотные характеристики (АФЧХ). Примеры перевода для рассматриваемого объекта показаны ниже.
bode(Wo_ss_d) % АФЧХ дискретного объекта представленного в форме пространства состояний
bode(Wo_tf_d) % АФЧХ дискретного объекта представленного в форме ПФ
bode(Wo_ss_c) % АФЧХ непрерывного объекта представленного в форме пространства состояний
bode(Wo_tf_c) % АФЧХ непрерывного объекта представленного в форме ПФ
grid % нанесение координатной сетки
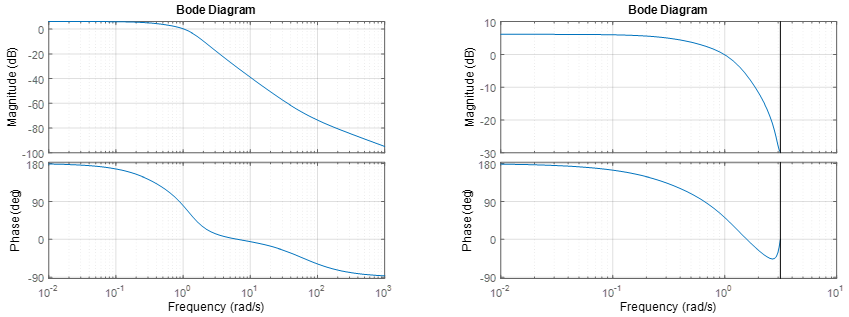
Рисунок 5. Амплитудно-фазовые частотные характеристики непрерывного объекта (слева) и дискретного объекта (справа).
Построение передаточной функции по частотным характеристикам
Имеется множество вариантов обратного перевода модели из частотной области. Вот один из них.
[mag,phase,freq] = bode(Wo_tf_c) % выделение амплитуды, фазы и частоты АФЧХ
complex_f = frd(mag.exp(jphase.pi/180),freq) % модель объекта в частотной области tfest(complex_f,3) % ПФ непрерывного объекта, 3 - порядок объекта
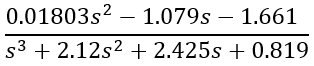
В этом примере зависимости амплитуды mag и фазы phase от частоты freq вычислены оператором bode для ПФ Wo_tf_c. Оператор frd сформировал структуру complex_f - зависимость комплексных аргументов mag.exp(jphase.pi/180) от частоты, которая использовалась оператором tfest для построения ПФ непрерывного объекта третьего порядка. Полученная ПФ точно совпадает с исходной ПФ Wo_tf_c. Как упоминалось во введении, при использовании экспериментальных зависимостей (амплитуды и фазы от частоты) мы бы получили неоднозначный вариант ПФ.
Перевод модели во временную область
MATLAB предлагает множество вариантов вычисления реакции объекта на входное воздействие. Вот один из них – реакция (Рисунок 6) на единичное ступенчатое воздействие вычисляется оператором step:
% [y,t] = step(Wo_tf_c) % выделение данных реакции на единичное воздействие
step(Wo_tf_c) % построение графика реакции на единичное воздействие
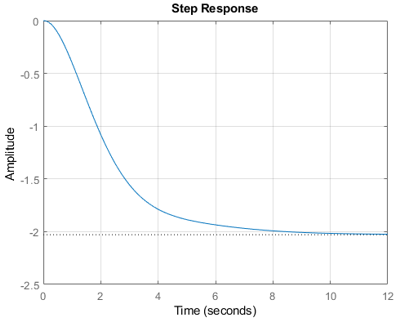
Рисунок 6. Реакция модели непрерывного объекта (ПФ: Wo_tf_c) на единичное ступенчатое воздействие.
Построение передаточной функции по временным характеристикам
Обратное преобразование – построение передаточной функции по временным характеристикам входа и выхода объекта выполняется командами iddata и tfest.
Перевод импульсной передаточной функции в код контроллера
Модель Рисунок 3 импульсной передаточной функции (3a) дискретного объекта (1) можно представить в виде схемы показанной на Рисунок 7.
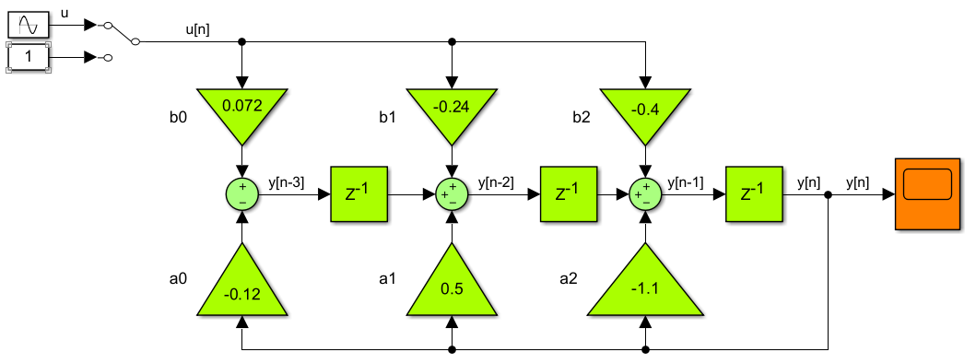
Рисунок 7. Модель импульсной передаточной функции

. Блок z-1 реализует задержку на 1 такт. Для рассматриваемого объекта установлен период дискретизации в 1 с.
Работа схемы Рисунок 7 подобна реализации Рисунок 8, в которой блок fcn, содержащий m-функцию пользователя, выполняет совместно с z-1 блоками работу рассматриваемой импульсной ПФ.

Рисунок 8. Simulink модель эквивалентной импульсной передаточной функции с fcn блоком, содержащим представленный m-код. Следующая программа вычисляет реакцию объекта, представленного импульсной ПФ. Полученная реакция (Рисунок 9) полностью совпадает с реакциями дискретных моделей рассматриваемого объекта и соответствует реакциям непрерывных моделей этого же объекта (Рисунок 10).
b2 = -0.4; b1 = -0.24; b0 = 0.072; % коэффициенты полинома числителя ИПФ
a3 = 1; a2 = -1.1; a1 = 0.5; a0 = -0.12; % коэффициенты полинома знаменателя ИПФ
y = zeros(1,50); % резервирование памяти для хранения реакции
u = ones(1,50); % единичное воздействие
ym1 = 0; ym2 = 0; ym3 = 0 % начальные значения
for i = 1:50
y(i) = a3*ym1; (7)
ym1 = b2*u(i)-a2*y(i)+ym2;
ym2 = b1*u(i)-a1*y(i)+ym3;
ym3 = b0*u(i)-a0*y(i);
end
% График реакции дискретных моделей
if 1
% Построение графиков
figure (1) % активное окно графопостроителя
clf % очистка предыдущих данных
plot(y,'xb') % график y[n] m-файла
hold on
plot(out.ScopeData1.signals(3).values) % график y[n] Simulink модели, ver.1
plot(out.ScopeData1.signals(4).values) % график y[n] Simulink модели, ver.2
plot(out.ScopeData1.signals(5).values) % график y[n] Simulink модели, ver.3
plot(out.ScopeData1.signals(6).values) % график y[n] Simulink модели, ver.4
legend('m-file','Simulink v.1','Simulink v.2','Simulink v.3','Simulink v.4')
grid
xlabel('Номер отсчета')
ylabel('Амплитуда реакции'),
title('Сравнение реакций дискретных моделей')
end
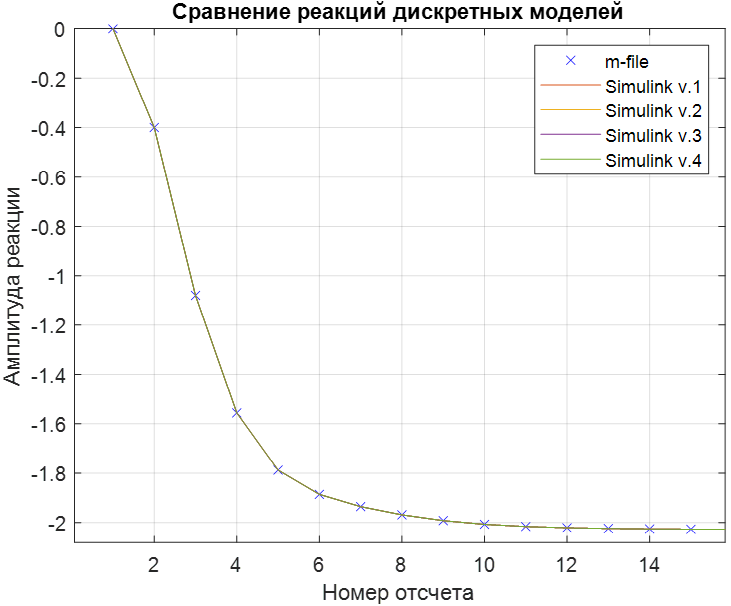
Рисунок 9. 100% совпадение реакций дискретных моделей и вычислений m-программы.
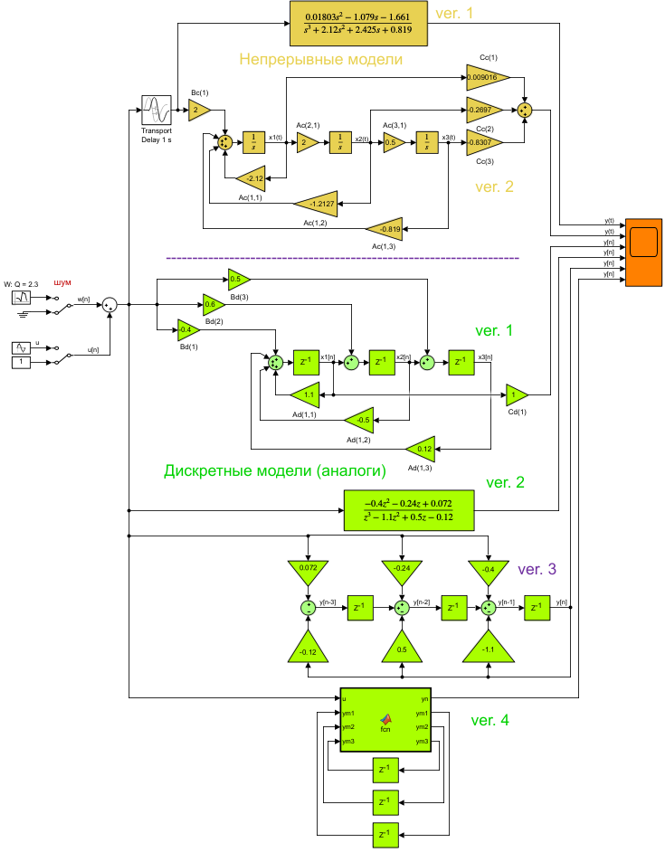
Рисунок 10. Варианты построения эквивалентных Simulink моделей рассматриваемого объекта.
Порядок программирования динамических моделей контроллерами
Для построения модели динамической системы средствами контроллеров предлагается выполнить следующее.
Средствами MATLAB преобразовать динамическую систему в форму импульсной передаточной функции для требуемого шага дискретизации (3a).
Выделить коэффициенты полиномов числителя и знаменателя импульсной ПФ (Рисунок 7)
Средствами контроллера реализовать последовательность вычисления импульсной ПФ (7)
Структура и порядок динамической системы могут отличаться от рассмотренного примера.
Заключение
Рассмотренные варианты преобразования форм представления динамических моделей в интегрированной среде MATLAB могут быть использованы для реализации моделей средствами контроллеров путем построения кода эквивалентной импульсной передаточной функции (Рисунок 11).
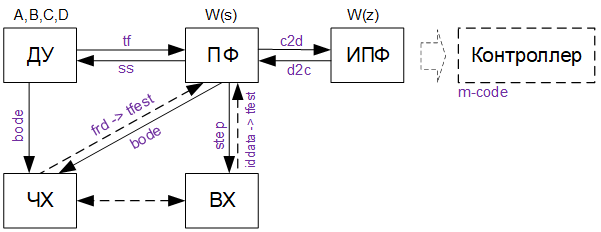
Рисунок 11. Операторы MATLAB преобразования моделей и построения эквивалентного кода для программирования контроллеров.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
А.А.Алексеев, Д.Х.Имаев, Н.Н.Кузьмин, В.Б.Яковлев. Теория управления: Учеб./СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 1999. – 435 с.
Help MATLAB.
Dr. Bob Davidov. Синтез наблюдателя состояний. http://portalnp.ru/2021/01/10862
Dr. Bob Davidov. Аналитическое конструирование линейно-квадратичного регулятора http://portalnp.ru/2021/01/10857
Dr. Bob Davidov. Фильтр Калмана в линейно-квадратичном гауссовском управлении. http://portalnp.ru/2021/02/10877
