
В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов.
Граф - это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними - за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина - точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро - неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге - не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность - вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.
Смежность вершин - две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер - два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще - две вершины смежные, если они соединены ребром, два ребра смежные - если они соединены вершиной.

Петля - ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф - граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершин��, поэтому у него есть своё название.

Кратные рёбра - рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф - граф с кратными рёбрами.
Псевдомультиграф - граф с петлями и кратными рёбрами.

Степень вершины - это количество рёбер, инцидентных указанной вершине. По-другому - количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.
Изолированная вершина - вершина с нулевой степенью.
Висячая вершина - вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф - это граф, в котором каждые две вершины соединены одним ребром.
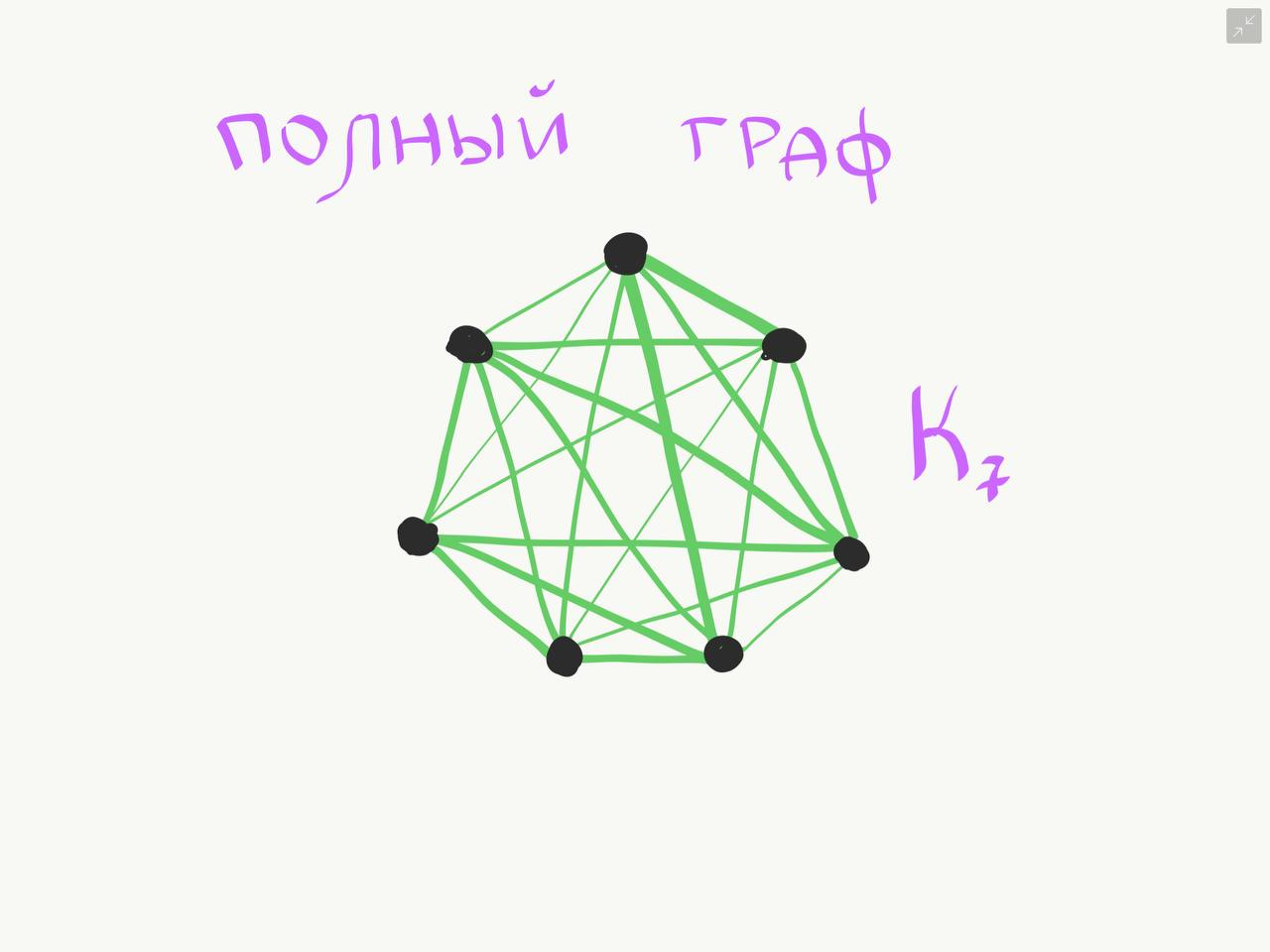
Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N - каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N - 1) / 2.
Регулярный граф - граф, в котором степени всех вершин одинаковые.

Двудольный граф - если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.
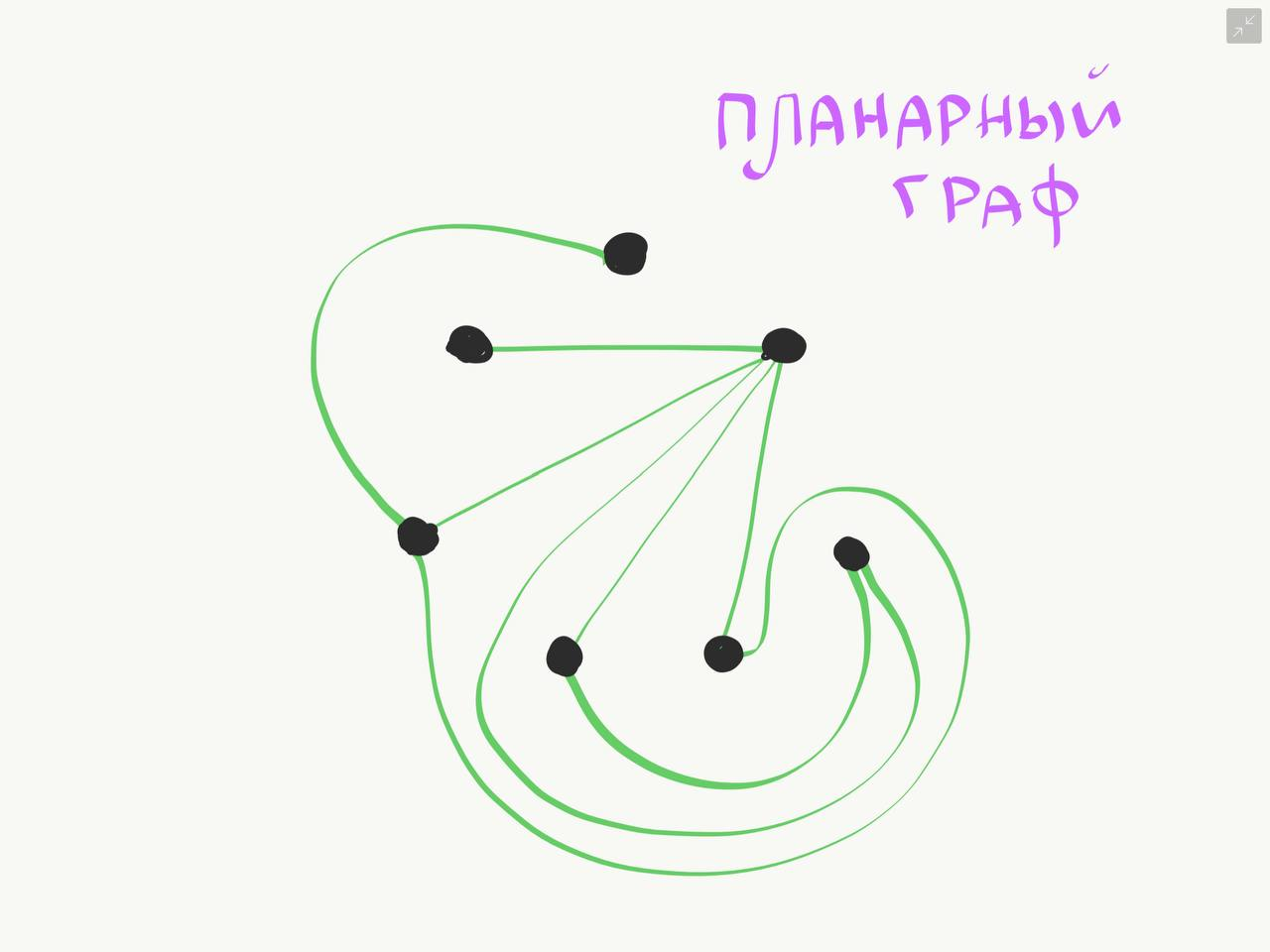
Если это невозможно сделать, то граф называется “непланарным”.
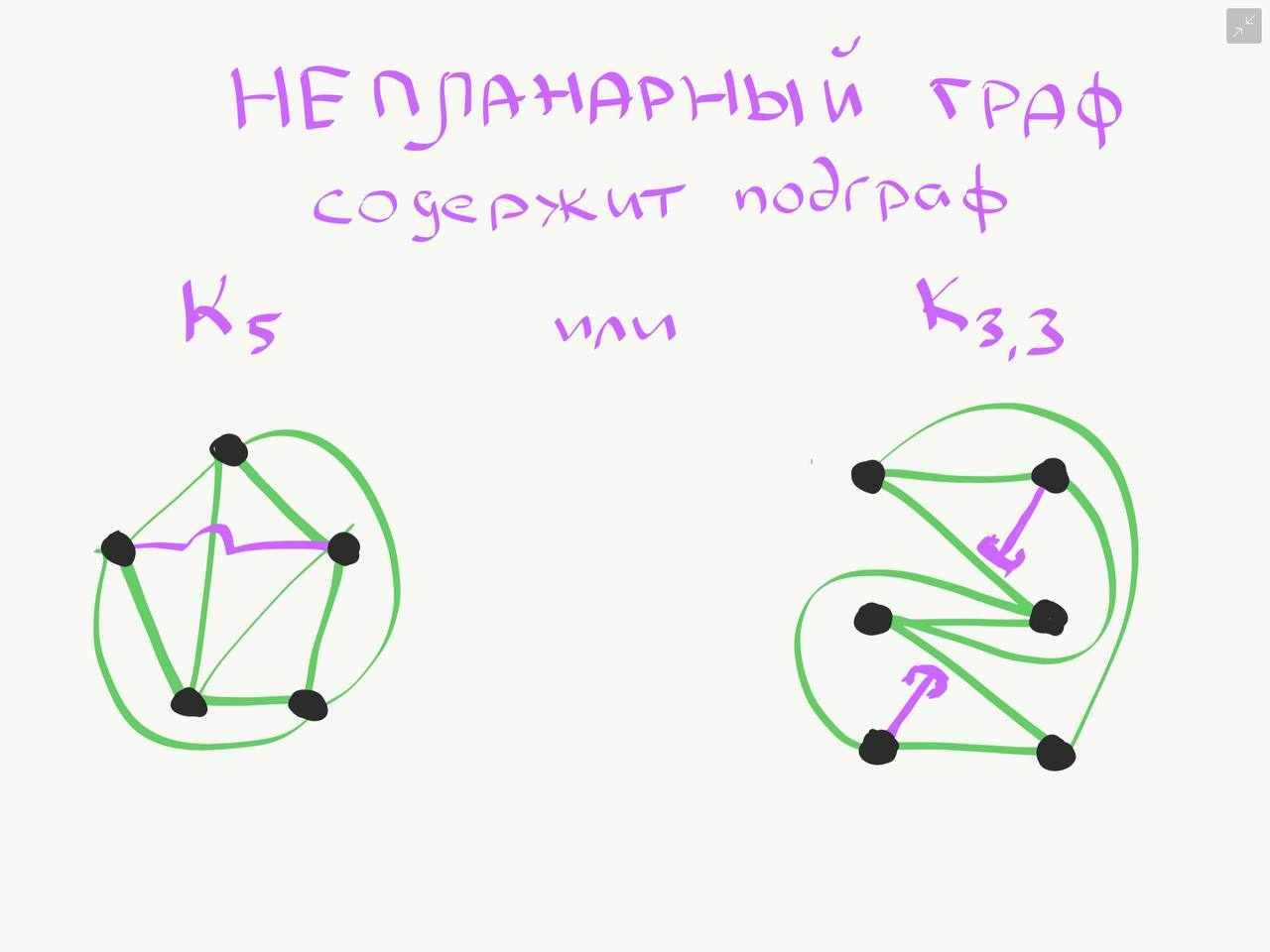
Минимальные непланарные графы - это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.
Путь или Маршрут - это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.
Длина пути - количество рёбер в пути.
Цепь - маршрут без повторяющихся рёбер.
Простая цепь - цепь без повторяющихся вершин.

Цикл или Контур - цепь, в котором последняя вершина совпадает с первой.
Длина цикла - количество рёбер в цикле.
Самый короткий цикл - это петля.

Цикл Эйлера - цикл, проходящий ��о каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона - цикл, проходящий через все вершины графа по одному разу. Другими словами - это простой цикл, в который входят все вершины графа.

Взвешенный граф - граф, в котором у каждого ребра и/или каждой вершины есть “вес” - некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса - “Алгоритмы и структуры данных”.
Связный граф - граф, в котором существует путь между любыми двумия вершинами.
Дерево - связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двои��ных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес - граф, в котором несколько деревьев.

Ориентированный граф или Орграф - граф, в котором рёбра имеют направления.
Дуга - направленные рёбра в ориентированном графе.

Полустепень захода вершины - количество дуг, заходящих в эту вершину.
Исток - вершина с нулевой полустепенью захода.
Полустепень исхода вершины - количество дуг, исходящих из этой вершины
Сток - вершина с нулевой полустепенью исхода.

Компонента связности - множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности - максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности - максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост - ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи - дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
