al-petrushin 31 июл 2021 в 13:12

Restricted Boltzmann Machine — физика для рекомендательных систем

5 мин

4.3K

Привет, Хабр, сегодня хочу предложить рассмотреть RBM модель для системы рекомендаций. Я думаю многие слышали о данном подходе для нейронных сетей, но именно в контексте рекомендательных систем информации на русском языке мало, хотя подход очень популярен. Здесь я сконцентрируюсь на математике, в свою очередь подсмотреть реализацию вы можете в репозитории recommenders Microsoft (https://github.com/microsoft/recommenders).

RBM — это модель генеративной нейронной сети, которая обычно используется для обучения без учителя. Основная задача RBM – изучить совместное распределение вероятностей $P(\upsilon,\ h)$ , где $\upsilon$ – видимые единицы, а – скрытые. Скрытые единицы представляют собой скрытые переменные, в то время как видимые единицы ограничены входными данными. Как только совместное распределение изучено, путем выборки из него создаются новые примеры.

Модель генерирует рейтинги для пары пользователь-объект, используя подход, основанный на совместной фильтрации. В то время как методы матричной факторизации изучают, как воспроизвести экземпляр матрицы сходства пользователей-объектов, RBM изучает лежащее в основе распределение вероятностей. Это дает несколько преимуществ:

Обобщаемость: модель хорошо обобщается на новые примеры, если они не сильно различаются по вероятности;
Стабильность во времени: если задача рекомендаций стационарна во времени, модель не нужно часто обучать, чтобы приспособиться к новым рейтингам / пользователям.

Стоит отметить, что данная модель – это неориентированная графическая модель, первоначально разработанная для изучения статистической механики илифизики магнитных систем. Статистическая механика обеспечивает вероятностное описание сложных систем, состоящих из огромного числа компонентов (обычно ∼10²³). Вместо того, чтобы смотреть на конкретный экземпляр системы, цель статической механики описать их типичное поведение. Этот подход оказался успешным для описания газов, жидкостей, сложных материалов например,полупроводников и даже знаменитого бозона Хиггса! Разработанный для обработки и организации больших объемов данных, алгоритм идеально подходит в современных алгоритмах обучения. В контексте рекомендательных систем идея состоит в том, чтобы изучить типичное поведение пользователя, а не конкретные примеры.

Основной величиной каждой модели статической механики является распределение Больцмана – это можно рассматривать как наименее смещенное распределение вероятностей на данном вероятностном пространстве $\Sigma$ и может быть получено с использованием принципа максимальной энтропии на пространстве распределений над $\Sigma$ . Его типичная форма:

$P=1/Ze^{(-\beta H)}$

где,– нормировочная константа, известная как статистическая сумма, $\beta$ – параметр шума с единицами обратной энергии; – гамильтониан или функция энергии системы.

По этой причине этот класс моделей в информатике также известен как энергетический. В физике $\beta$ — это обратная температура системы в единицах постоянной Больцмана, но здесь мы фактически изменим масштаб внутри, так что теперь это натуральное число.описывает поведение двух наборов стохастических векторов, обычно называемых v_i и h_j Первые составляют вход и выход алгоритма, а скрытые единицы — это скрытые факторы, которые мы хотим изучить. Эта структура приводит к следующей топологии нейронной сети:

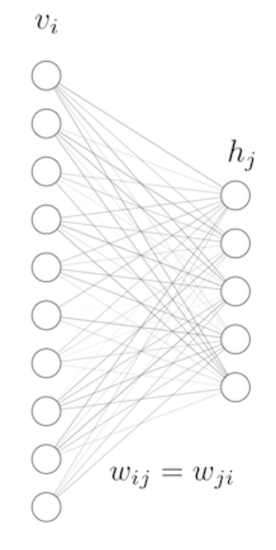
Теперь ближе к алгоритму. Входные данные выборки, которая используется разработчиком, состоят из оценок от 1 до 5. Таким образом, мы будем рассматривать дискретное конфигурационное пространство видимых переменных, каждая из которых принимает значения в конечном множестве $\chi_v= {\ \{1,2,3,4,5} \}$ . Глобальная конфигурация системы определяется следующим образом: $v = {\ \{v_1,\ v_2,\ \ldots,\ v_m} \} \in\chi_v^m$ и назначается 0 для объекта без рейтинга. В добавок также указываются скрытые блоки, которые мы принимаем в качестве случайных двоичных величин $\chi_h={\{0,1}\}$ , обозначающих, активен конкретный блок или нет, и $h\ =\left\{h_1,\ h_2,\ \ldots,\ h_n\right\}\ \in\chi_h^n$ . Скрытые блоки могут описывать скрытые атрибуты объекта, дляфильмов−жанр,длястатей−областьисследованияит.д.. Минимальная модель такой системы определяется следующим гамильтонианом:

$H=-\sum_{i,j\ \in\ G}{v_iw_{ij}h_j-\sum_{i=1}^{m}{v_ia_i-\sum_{j=1}^{n}{h_ib_i}}}$

Первый член — это «термин взаимодействия», фиксирующий корреляции между видимыми и скрытыми единицами, в то время как два других члена являются «потенциальными терминами», принимая во внимание предвзятость единиц. Корреляционная матрица $w_{ij}$ и два смещения a_i и b_i являются параметрами обучения, которые должны быть зафиксированы путем минимизации правильно определенной функции стоимости. При этом нельзя напрямую минимизировать функцию ошибок между прогнозируемыми и оригинальными данными. Как и в любой задаче статической механики, правильной величиной, которую нужно минимизировать, является свободная энергия (при этом в нашем случае $\beta=1$ ).

$F=\ -\log{Z}=-log\sum_{v_i,\ \ h_i}{P(v,h)}$

На языке теории вероятностей указанная выше величинаявляется кумулянтной производящей функцией. Одним из способов оценки свободной энергии является использование алгоритма выборки Монте-Карло с цепью Маркова, но здесь мы будем использовать вместо этого приближенный метод, называемый контрастной дивергенцией, основанный на выборке Гиббса. Его преимущество, в том, что он быстрее Монте-Карло. Как только кандидатбыл найден, мы фиксируем параметры обучения, минимизируя .

Рассмотрим модель более подробно. Вместо выборки непосредственно из совместного распределения вероятностей можно оценить условные распределения:

где второе равенство следует из того, что модель неориентирована или физически находится в равновесии. Выборка Гиббса по существу состоит из двух этапов, называемых положительной и отрицательной фазами.

Позитивная фаза начинается с фиксации видимых блоков в данных и определении $P\left(h_j=1\ |\ v\right)$ , то есть определение вероятности того, что j-й скрытый блок активен для всего входного вектора. На практике производящую функцию удобно оценивать как:

$Z[v, b]=\prod_{j}\sum_{h_j=0,1}{e^{h_j(\sum_{i}{w_{ij}v_i\ +\ b_j})}=\prod_{j}{(1\ +\ e^{\sum_{i}{w_{ij}v_i\ +\ b_j}})}}$

Взяв градиенты по смещению, получим:

$\frac{\partial}{\partial b_j}\log{Z[v,b]}=\frac{1}{1+e^{-(\sum_{i}{w_{ij}v_i\ +\ b_j})}}=\sigma(\phi_j(v,b))$

где $\phi_j\left(v,\ b\right)=\sum_{i}{w_{ij}v_i}+b_j$ , и логистическая функция идентифицируется как $\sigma\left(\bullet\right)\equiv P\left(h_j=1\ |\ v,b\right).$ Собственно $\sigma$ используется, чтобы выбрать значение h_j .

В свою очередь негативная фаза включает использование выборочного значения скрытых единиц, чтобы определить $P\left(v_i=q\ |\ h\right),$ , где q = 1, ..., 5 . Это дается полиномиальным выражением:

$P(v_i=q\ |\ h,a)=\prod_{v_i=1}^{q}e^{v_i(\sum_{i}{w_{ij}h_j\ +\ a_i})/Z_q}$

где Z_q – статистическая сумма, вычисленная по результатам . Далее, выбираются значения v_i из приведенного выше распределения. Разумеется, что эти новые v_i не обязательно являются теми, которые мы использовали в качестве входных данных, по крайней мере, не в начале обучения. Вышеупомянутые шаги повторяются ? раз, причем ? обычно увеличивается во время тренировки в соответствии с заданным значением.

В конце каждой k-шаговой выборки Гиббса расчитывается разница между начальной свободной энергией при ? = 1 и заданном v и энергией после k-шагов и обновляются параметры обучения $w_{ij}$ , b_i , a_i , путем дифференцирования .

Этот процесс повторяется для каждой обучающей эпохи, до тех пор, пока ∆F=0 , то есть изученное распределение точно воспроизводит эмпирическое. В этом смысле v_i служит как входом, так и выходом модели. Поскольку $w_{ij}$ содержит информацию о том, как соотносятся оценки пользователей, мы можем использовать эту информацию для создания рейтингов для неоцененных объектов путем выборки из изученного предельного распределения:

$v_i=\sum_{v_i}{P(v)}$

На этом вообщем-то и все! Как упоминалось выше, реализацию можно посмотреть у Microsoft. Она достаточно хорошо задокументирована и предоставляет простые примеры с использованием RBM.

Исследуйте и развивайтесь!

Теги:

Хабы:

Restricted Boltzmann Machine — физика для рекомендательных систем

Публикации

Истории

Работа

Ближайшие события