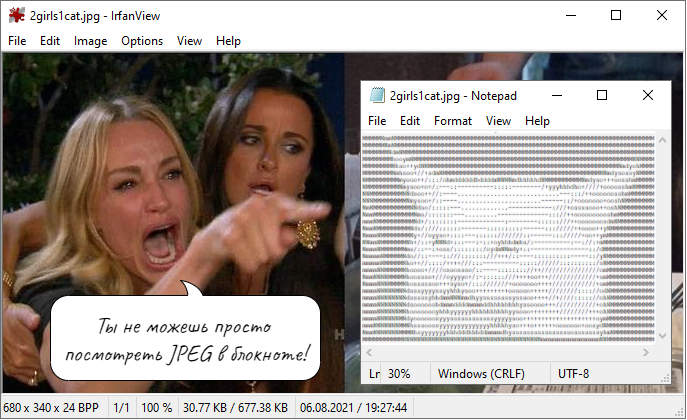
Если открыть произвольный JPEG-файл в блокноте, то можно увидеть лишь хаотичный набор символов. Отсюда вопрос: возможно ли закодировать изображение так, чтобы его было можно просмотреть не только обычным способом, но и в обычном блокноте, в виде ASCII-графики. Ответ положительный, если использовать максимальное сжатие:
Grayscale (только оттенки серого).
Обнулить все AC-коэффициенты, то есть весь блок 8x8 пикселей сделать одноцветным.
Задать максимальный шаг квантования DC-коэффициента - 255. Это ограничивает цвет всего 9 оттенками серого: 0, 32, 64, 96, 128, 160, 192, 224, 255.
Вот так:

Да, не очень впечатляет. Но, тем не менее, это все еще JPEG, каждый блок 8x8 которого закодирован одним ASCII-символом:

Практическое применение отсутствует. Просто забавно.
Минимум теории
Для каждого блока 8x8 пикселей выполняется дискретное косинусное преобразование, результатом которого является один DC- и 63 AC-коэффициента. DC-коэффициент может принимать значения от -1020 до 1020 (255*4). Для grayscale-изображения минимальному значению соответствует черный цвет, максимальному - белый. В случае, если весь блок полностью одноцветен, все 63 AC-коэффициента равны 0.
Затем коэффициенты квантуются, то есть делятся на некоторое число и округляются. Наибольший возможный шаг квантования - 255. Это максимальный уровень сжатия. Тогда DC-коэффициенты принимают значения от -4 до 4. При записи в файл используется дельта-кодирование: сохраняются разности квантованных коэффициентов текущего и предыдущего блоков. То есть, при шаге квантования 255, дельта-значения могут быть от -8 до 8. Например, если изображение начинается с двух белых блоков после которых идет черный (4, 4, -4), то последовательность будет записана как: 4, 0, -8.
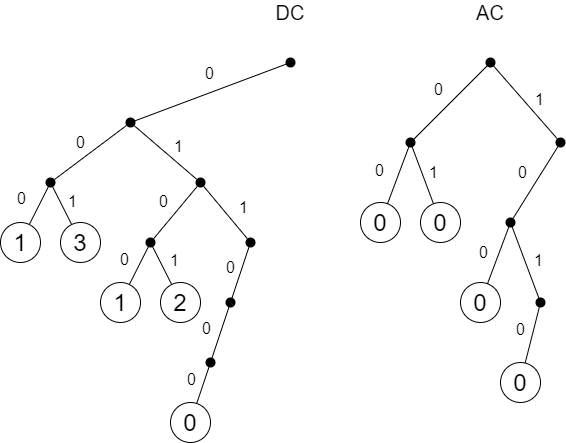
Коэффициенты записываются с помощью кодов (деревьев) Хаффмана. Эти коды хранятся в самом JPEG-файле. Для серого изображения нужно 2 дерева - одно для DC, другое для AC. Для решаемой задачи деревья были построены специальным образом.
Декодирование
Битовый поток начинается с байта 0xA, то есть 00001010 в двоичном представлении. Это символ переноса строки, который необходим в самом начале, иначе ASCII-графика окажется на одной строке вместе с заголовком JPEG. Декодер при чтении этих битов проходит по дереву Хаффмана, каждый раз выбирая ветвь в зависимости от значения бита.
Чтение 3 битов 000 приводит к листу со значением 1. Это означает, что нужно прочитать 1 следующий бит 0, чтобы получить DC-коэффициент. Если первая цифра значения в двоичном представлении — 1, то оставляем как есть: DC = <значение>. Иначе преобразуем: DC = <значение>-2^<длина значения>+1. В нашем случае DC = 0 - 2^1 + 1 = -1. Обратите внимание, что если последовательность битов начинается на 011000, то значение листа равно нулю. В этом случае DC = 0.
Далее опять осуществляется проход по дереву Хаффмана, но уже для AC-коэффициентов. Биты 1010 приводят к листу со значением 0. Как можно видеть, других значений в этом дереве нет. Ноль означает, что нужно прекратить чтение AC-коэффициентов и обнулить оставшиеся. Поэтому в нашем случае все AC-коэффициенты равны нулю и в этом блоке и во всех других.
Весь остальной поток читается аналогично, но, как уже было сказано: начиная со второго блока читаются не сами DC-коэффициенты, а разности (дельты) между коэффициентом текущего и предыдущего блоков. Используемое дерево Хаффмана для DC-коэффициентов позволяет закодировать максимум 3-битные дельты — от -7 до 7. Значит крайние значения DC должны различаться не более чем 7. Например, от -3 до 4 (то есть совсем черный цвет уже не получится). Добавить 4-битный код у меня нормально не получилось.
Все встречаемые символы приведены в следующей таблице.
HEX ASCII DC AC Дельта
60 ` [011000 00] 0
4C L [0100 1 100] +1
44 D [0100 0 100] -1
58 X [0101 10 00] +2
54 T [0101 01 00] -2
5C \ [0101 11 00] +3
50 P [0101 00 00] -3
30 0 [001 100 00] +4
2D - [001 011 01] -4
34 4 [001 101 00] +5
28 ( [001 010 00] -5
38 8 [001 110 00] +6
24 $ [001 001 00] -6
3C < [001 111 00] +7
21 ! [001 000 01] -7
10 LF [000 0 1010] 1 Было бы хорошо, например, белый блок кодировать пробелом. Но из-за дельта-кодирования мы можем лишь сопоставить символам разность цветов соседних блоков. Это тоже неплохо, так как разность цветов позволяет четко выделить границы объектов на изображении. Тогда почему бы не использовать пробел для одноцветных блоков? У него неудобное двоичное представление 00100000 из-за которого у меня не получилось использовать 3-битные дельты. Пришлось искать какой-нибудь альтернативный символ. Самый малозаметный - обратный апостроф ( ` ).
Символ переноса строки не только "рисует" мусорный столбец на изображении, но уменьшает дельту на 1. Поэтому после него добавляется символ L, восстанавливающий дельту.
Все это реализовано с помощью простейшей программы на Питоне (Github), позволяющей генерировать jpg-файл в описанном формате по любому исходному изображению.
Пример. Можно скачать и проверить. В новой версии Хабра нужно сначала щелкнуть по картинке, так как отображается пережатая версия. Или скачать картинку по прямой ссылке.

