
Специалисты по анализу данных часто оценивают свои прогностические модели с точки зрения точности и погрешности, но редко спрашивают себя:
«Способна ли моя модель спрогнозировать реальные вероятности?»
Однако точная оценка вероятности чрезвычайно ценна с точки зрения бизнеса (иногда она даже ценнее погрешности). Хотите пример?
Представьте, что ваша компания продает два вида кружек: обычные белые кружки и кружки с котятами. Вам нужно решить, какую из кружек показать клиенту. Для этого нужно предсказать вероятность того, что пользовать может купить ту или другую кружку. Вы обучили пару моделей и у вас есть следующие результаты:
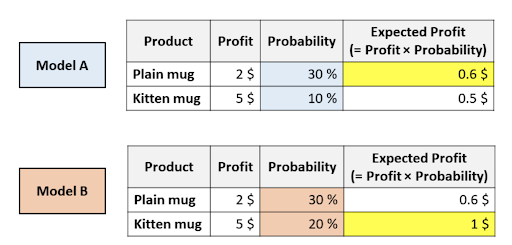
Итак, какую из кружек вы бы предложили пользователю?
Обе модели решили, что пользователь с наибольшей вероятностью купит обычную кружку (таким образом, у модели А и модели B одинаковая область под кривой ошибок, поскольку этот показатель оценивает только сортировку).
Но согласное модели А, вы сможете максимизировать ожидаемую прибыль, рекомендуя обычную кружку. Тогда как по модели B ожидаемая прибыль будет максимальной при выборе кружки с котенком.
В такие моменты жизненно важно выяснить, какая из моделей точнее оценивает вероятности (как визуально, так и численно) и как «подправить» имеющуюся модель, чтобы увеличить точность.
Что не так с predict_proba
У всех самых популярных библиотек машинного обучения есть метод под названием «predict_proba», это относится к Scikit-learn (например, LogisticRegression, SVC, randomForest,...), XGBoost, LightGBM, CatBoost, Keras…
Но несмотря на свое название predict_proba не совсем предсказывает вероятности. На самом деле, различные исследования (особенно это и это) показали, что самые популярные прогностические модели не откалиброваны.
Того факта, что число находится между нулем и единицей, уже достаточно, чтобы называть его вероятностью!
Но когда мы можем сказать, что число в самом деле представляет из себя вероятность?
Представьте, что вы обучили прогностическую модель, чтобы предсказать, разовьется ли у пациента рак. Допустим, что для данного пациента модель предсказывает вероятность 5%. По идее мы должны пронаблюдать одного и того же пациента в нескольких параллельных вселенных и посмотреть, действительно ли у него разовьется рак в 5% случаев.
Поскольку мы не можем идти по этому пути, лучшим прокси-сервером будет взять всех пациентов с вероятностью заболевания 5%, и по��считать, у скольких из них развился рак. Если наблюдаемый процент на самом деле близок к 5%, мы говорим, что вероятности, выдаваемые моделью, откалиброваны.
Когда предсказанные вероятности отражают реальные базовые вероятности, они называются “откалиброванными”.
Но как проверить, откалибрована ли ваша модель?
Калибровочная кривая
Самый простой способ оценить калибровку вашей модели – это построить график, называемый «калибровочной кривой» (он же – диаграмма надежности).
Идея состоит в том, чтобы разделить наблюдения на ячейки вероятности. Таким образом, наблюдения, принадлежащие к одной и той же ячейке, имеют одинаковую вероятность. Итак, для каждой ячейки калибровочная кривая сравнивает спрогнозированное среднее (т.е. среднее значение предсказанной вероятности) с теоретическим средним (т.е. средним наблюдаемой целевой переменной).
Scikit-learn сделает все за вас с помощью функции calibration_curve:
from sklearn.calibration import calibration_curve
y_means, proba_means = calibration_curve(y, proba, n_bins, strategy)Вам нужно только выбрать количество ячеек и (необязательно) стратегию распределения по ячейкам:
«Uniform» - интервал от 0 до 1 разделенный на n_bins одинаковой ширины;
«quantile» - границы ячеек распределяются таким образом, чтобы в каждой ячейке было одинаковое количество наблюдений.
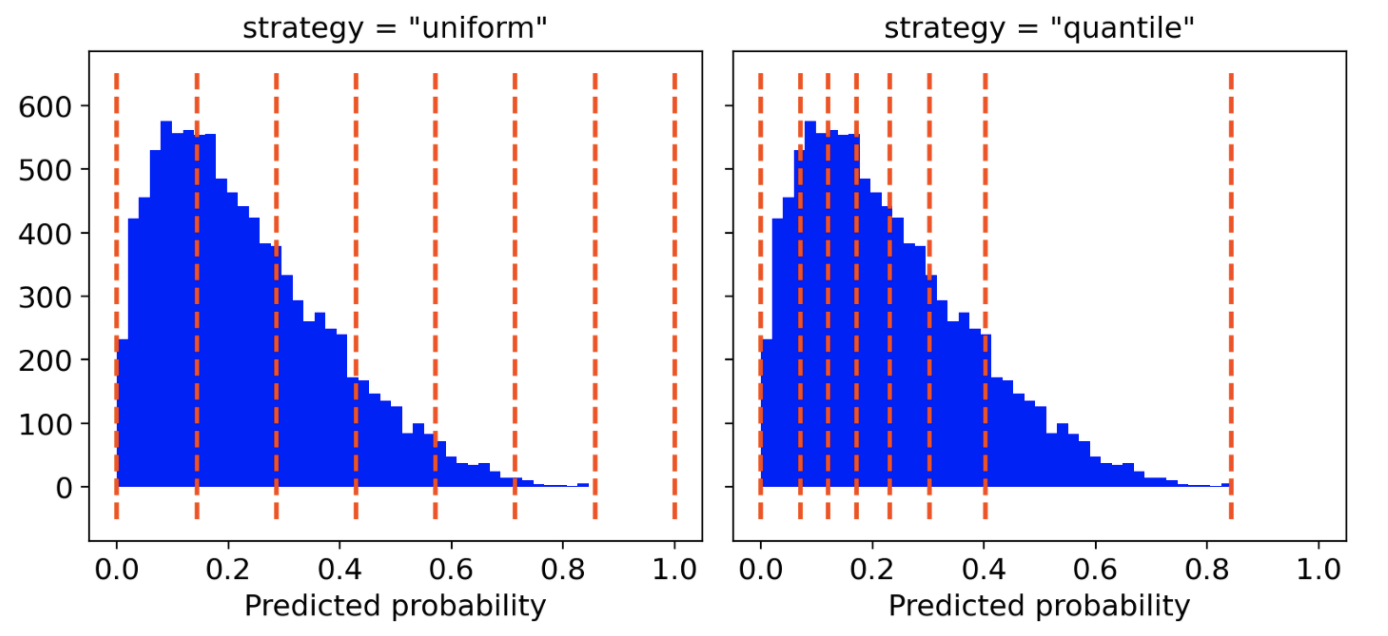
Для построения графиков лично я предпочитаю подход «quantile». На самом деле «Uniform»-распределение может дезориентировать, поско��ьку в некоторых ячейках может быть крайне мало наблюдений.
Функция Numpy возвращает два массива, содержащих среднюю вероятность и среднее значение целевой переменной для каждой ячейки. Поэтому все, что нам нужно сделать – это нарисовать график:

Предположим, что у вашей модели хорошая точность, тогда калибровочная кривая будет монотонно увеличиваться. Но это не значит, что модель хорошо откалибрована.
На самом деле, ваша модель хорошо откалибрована только в том случае, если калибровочная кривая очень близка к биссектрисе (т.е. серой пунктирной линии), поскольку это будет означать, что прогнозируемая вероятность в среднем близка к теоретической вероятности.
Давайте рассмотрим несколько примеров распространенных типов калибровочных кривых, которые указывают на неверную калибровку вашей модели:
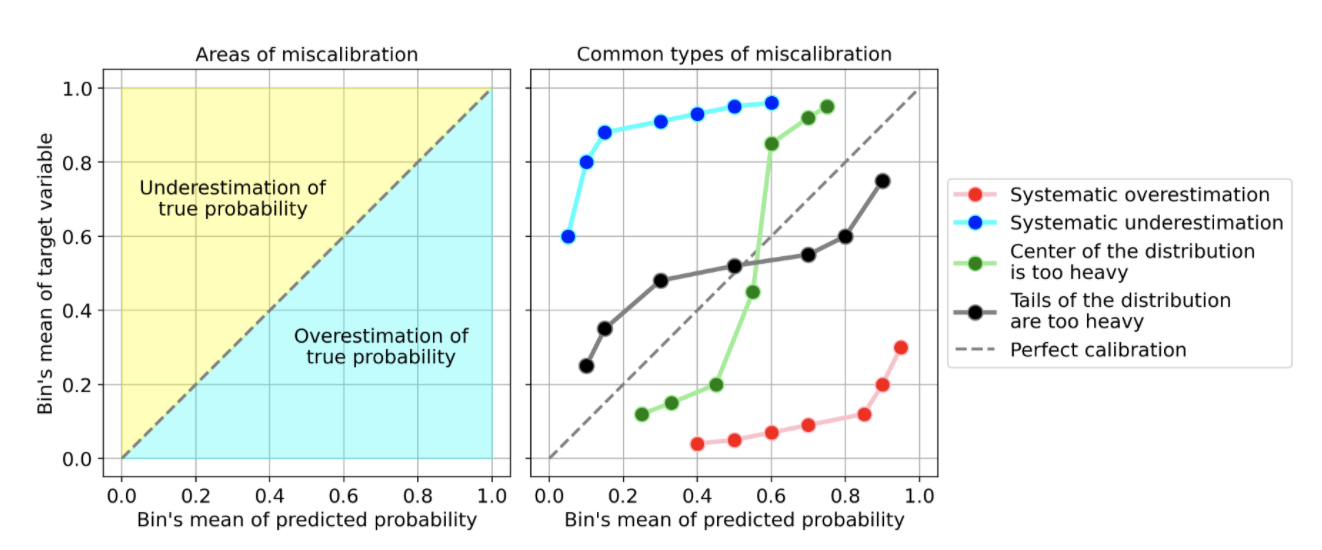
Наиболее распространенными типами неправильной калибровки являются:
Систематическая переоценка. По сравнению с правильным распределением распределение прогнозируемых вероятностей смещается вправо. Так часто случается, когда вы обучаете модель на несбалансированном наборе данных с очень небольшим количеством положительных наблюдений.
Систематическая недооценка. По сравнению с правильным распределением распределение прогнозируемых вероятностей смещается влево.
Центр распределения слишком тяжелый. Так происходит, когда «такие алгоритмы, как метод опорных векторов или ускоренные деревья решений, имеют тенденцию отклонять прогнозируемые вероятности от 0 и 1» (цитата из "Прогнозирования хороших вероятностей при обучении с учителем").
Хвосты распределения слишком тяжелые. Например, «Другие методы, такие как наивный байес, имеют противоположный уклон, и, как правило, приближают прогнозы к 0 и 1» (цитата из "Прогнозирования хороших вероятностей при обучении с учителем").
Как исправить неправильную калибровку на Python
Допустим, вы обучили классификатор, который выдает точные, но некалиброванные вероятности. Идея калибровки вероятности состоит в том, чтобы построить вторую модель (называемую калибратором), которая способна исправлять имеющиеся вероятности до реальных.
Обратите внимание, что калибровку не следует проводить на тех же данных, которые использовались для обучения первого классификатора.
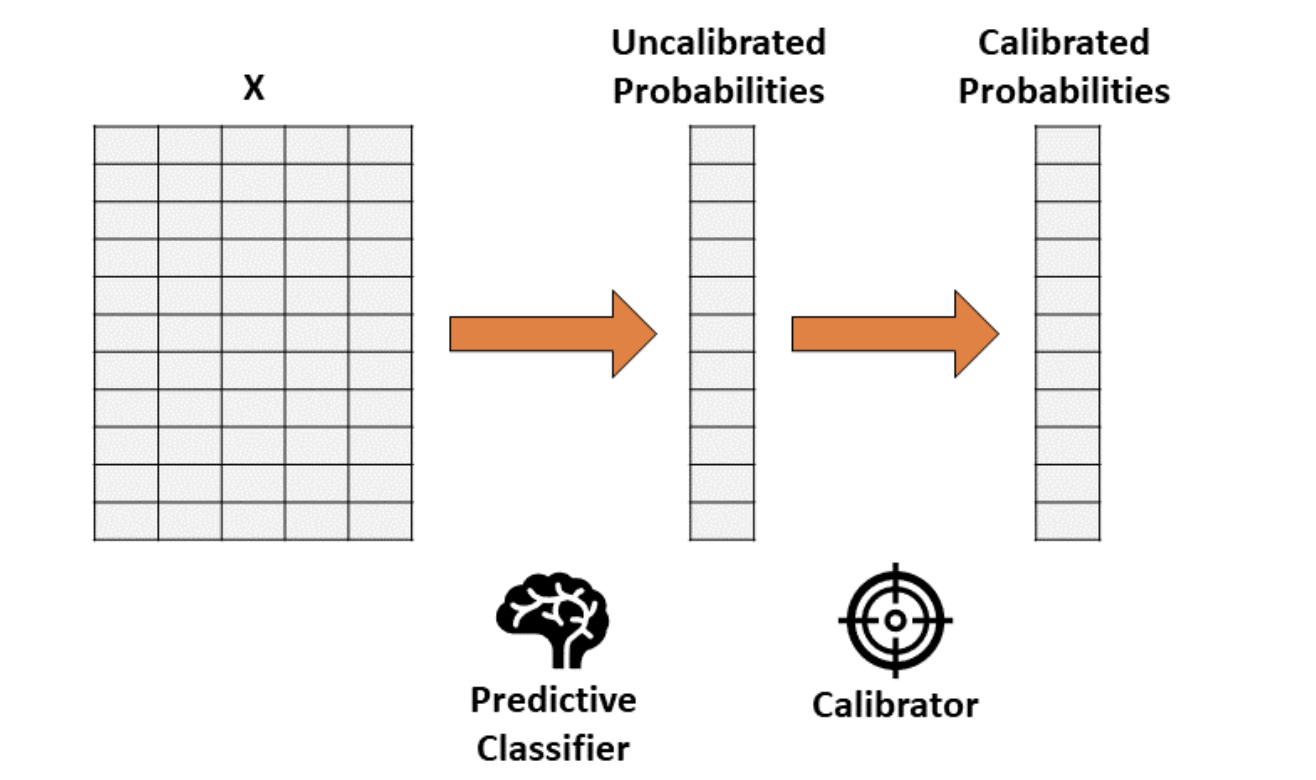
Таким образом, калибровка – это функция, которая преобразует одномерный вектор (некалиброванных вероятностей) в другой одномерный вектор (калиброванных вероятностей).
Для калибровки в основном используются два метода:
Изотоническая регрессия. Непараметрический алгоритм, который подгоняет неубывающую линию свободной формы под данные. Тот факт, что линия неубывающая, является основополагающим, поскольку так учитывается исходная сортировка.
Логистическая регрессия.
Давайте посмотрим, как использовать калибраторы на практике в Python, с помощью игрушечного набора данных.
from sklearn.datasets import make_classification
X, y = make_classification(
n_samples = 15000,
n_features = 50,
n_informative = 30,
n_redundant = 20,
weights = [.9, .1],
random_state = 0
)
X_train, X_valid, X_test = X[:5000], X[5000:10000], X[10000:]
y_train, y_valid, y_test = y[:5000], y[5000:10000], y[10000:]Для начала нам нужно будет обучить классификатор. Давайте воспользуемся случайным лесом (но с любой другой моделью, у которой есть метод predict_proba, все будет в порядке).
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier().fit(X_train, y_train)
proba_valid = forest.predict_proba(X_valid)[:, 1]Затем мы используем выходные данные классификатора (по данным валидации) для обучения калибратора и, наконец, для прогнозирования вероятностей по тестовым данным.
Изотоническая регрессия
from sklearn.isotonic import IsotonicRegression
iso_reg = IsotonicRegression(y_min = 0, y_max = 1, out_of_bounds = 'clip').fit(proba_valid, y_valid)
proba_test_forest_isoreg = iso_reg.predict(forest.predict_proba(X_test)[:, 1])Логистическая регрессия
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression().fit(proba_valid.reshape(-1, 1), y_valid)
proba_test_forest_logreg = log_reg.predict_proba(forest.predict_proba(X_test)[:, 1].reshape(-1, 1))[:, 1]На данный момент у нас есть три варианта прогнозирования вероятностей:
Обычный случайный лес
Случайный лес + изотоническая регрессия
Случайный лес + логистическая регрессия
Но как понять, какой из них ��учше откалиброван?
Количественная оценка неправильной калибровки
Всем нравятся графики. Но помимо графика калибровки, нам нужен количественный способ измерения (неправильной) калибровки. Наиболее часто используемая метрика называется ожидаемой ошибкой калибровки. Она отвечает на вопрос: насколько далеко в среднем наша спрогнозированная вероятность от настоящей вероятности?
Возьмем, например, один классификатор:
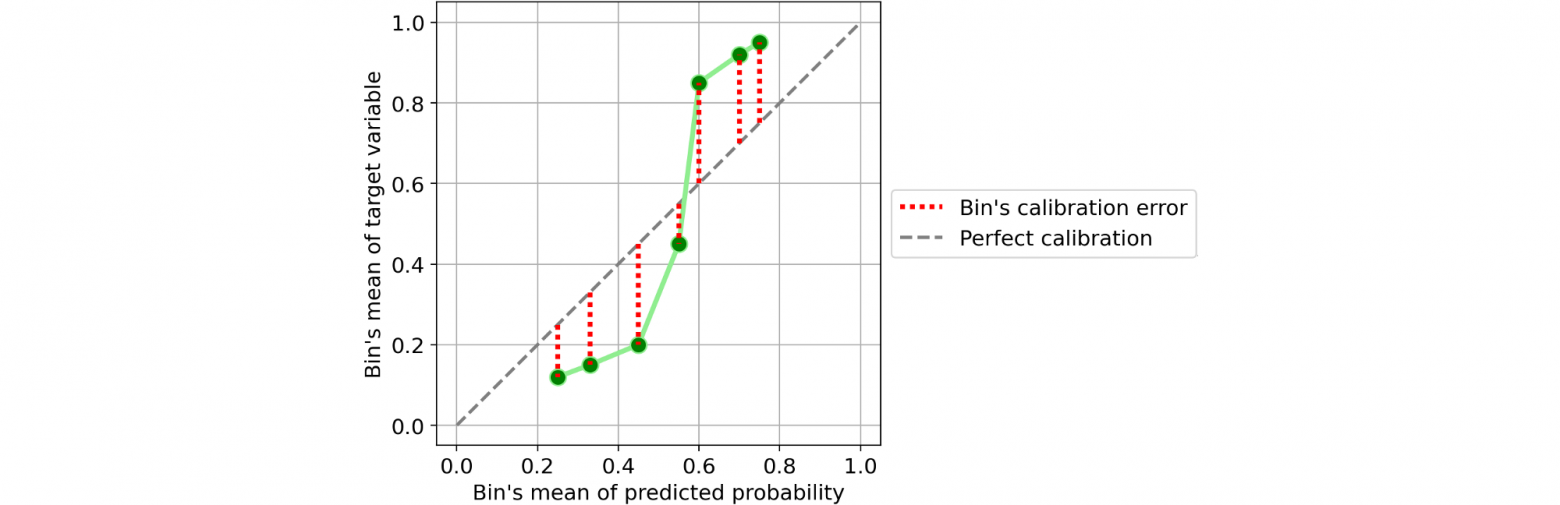
Легко определить погрешность калибровки одной ячейки: нужно взять модуль разности среднего значения прогнозируемых вероятностей и доли положительных результатов в рамках одной ячейки.
Если подумать, то все интуитивно понятно. Возьмем одну ячейку и предположим, что среднее значение ее прогнозируемых вероятностей 25%. Таким образом, мы ожидаем, что доля положительных результатов в этой ячейке примерно равна 25%. Чем дальше имеющееся значение от 25%, тем хуже калибровка этой ячейки.
Таким образом, ожидаемая ошибка калибровки (ЕСЕ) представляет собой средневзвешенное значение ошибок калибровки отдельных ячеек, где каждая ячейка весит пропорционально количеству наблюдений, которые она содержит:
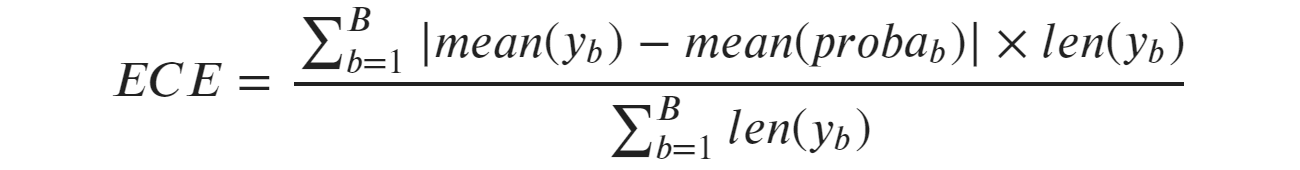
где b-определяет ячейку, а B – количество ячеек. Обратите внимание, что в знаменателе у нас просто общее число сэмплов.
Но в этой формуле остается проблема определения количества ячеек. Чтобы найти наиболее нейтральную метрику, я предпочитаю определять количество ячеек по правилу Фридмана-Диакониса (статистическое правило, предназначенное для определения количества ячеек, которое делает гистограмму максимально близкой к теоретическому распределению вероятностей).
Использовать правило Фридмана-Диакониса в Python очень просто, поскольку оно уже реализовано в функции histogram в numpy (нужно лишь передать строку «fd» в параметр «bins»).
Вот реализация ожидаемой ошибки калибровки на Python, с правилом Фридмана-Диакониса по умолчанию:
def expected_calibration_error(y, proba, bins = 'fd'):
import numpy as np
bin_count, bin_edges = np.histogram(proba, bins = bins)
n_bins = len(bin_count)
bin_edges[0] -= 1e-8 # because left edge is not included
bin_id = np.digitize(proba, bin_edges, right = True) - 1
bin_ysum = np.bincount(bin_id, weights = y, minlength = n_bins)
bin_probasum = np.bincount(bin_id, weights = proba, minlength = n_bins)
bin_ymean = np.divide(bin_ysum, bin_count, out = np.zeros(n_bins), where = bin_count > 0)
bin_probamean = np.divide(bin_probasum, bin_count, out = np.zeros(n_bins), where = bin_count > 0)
ece = np.abs((bin_probamean - bin_ymean) * bin_count).sum() / len(proba)
return eceТеперь, когда у нас есть метрика для калибровки, давайте сравним калибровку трех моделей, которые у нас были выше (на тестовом наборе):

В нашем случае изотоническая регрессия обеспечила наилучший результат с точки зрения калибровки, в среднем с отклонением 1.2% от реальной вероятности. Это гигантское улучшение, если учитывать, что ECE обычного случайного леса составила 7%.
Источники
Вот несколько интересных работ, которые легли в основу этой статьи, и я их могу вам рекомендовать, если вы хотите углубиться в тему калибровки вероятности:
Predicting good probabilities with supervised learning (2005) от Caruana и Niculescu-Mizil.
On Calibration of Modern Neural Networks (2017) от Guo и др.
Obtaining Well Calibrated Probabilities Using Bayesian Binning (2015) от Naeini и др.
Материал подготовлен в рамках курса «Machine Learning. Advanced».
Всех желающих приглашаем на открытый урок «Multi-armed bandits для оптимизации AB тестирования, от теории — сразу в бой». На этом вебинаре мы разберем один из самых простых, но эффективных вариантов применения обучения с подкреплением. Посмотрим, как можно переформулировать задачу АБ тестирования в задачу байесовского вывода и получать выводы по тестам раньше, чем при классическом тестировании.
→ РЕГИСТРАЦИЯ
