Залогом успешного применения ML к конкретной бизнес-задаче является не только правильно подобранная модель, но и признаки, на которых модель обучается. Давайте на примере задачи поведенческого банковского скоринга разберёмся в том, почему важно уделять внимание мультиколлинеарности признаков в линейных моделях и научимся от неё избавляться.
Признаки — это набор данных, который описывает изучаемое в задаче явление. Не все признаки могут быть полезны, поэтому их отбор является важным этапом моделирования. Есть много причин, по которым включение тех или иных признаков в модель может привести к неудовлетворительным результатам. Одна из них — мультиколлинеарность.
Мультиколлинеарность — явление, при котором наблюдается сильная корреляция между признаками. Чтобы оценить степень корреляции между парой количественных признаков, вычисляют, например, коэффициент корреляции Пирсона — меру линейной связи между ними. Если абсолютное значение коэффициента превышает некоторый порог, то можно говорить о наличии сильной корреляции между признаками. На практике пороговое значение зависит от задачи и находится в диапазоне от 0.6 до 1.0.
Например, у нас есть два признака: зарплата в рублях и зарплата в долларах. Очевидно, что два этих признака зависимы и между ними существует линейная связь. Коэффициент корреляции Пирсона для них будет равен 1, поэтому включение этой пары в множество признаков для моделирования приведет к мультиколлинеарности.
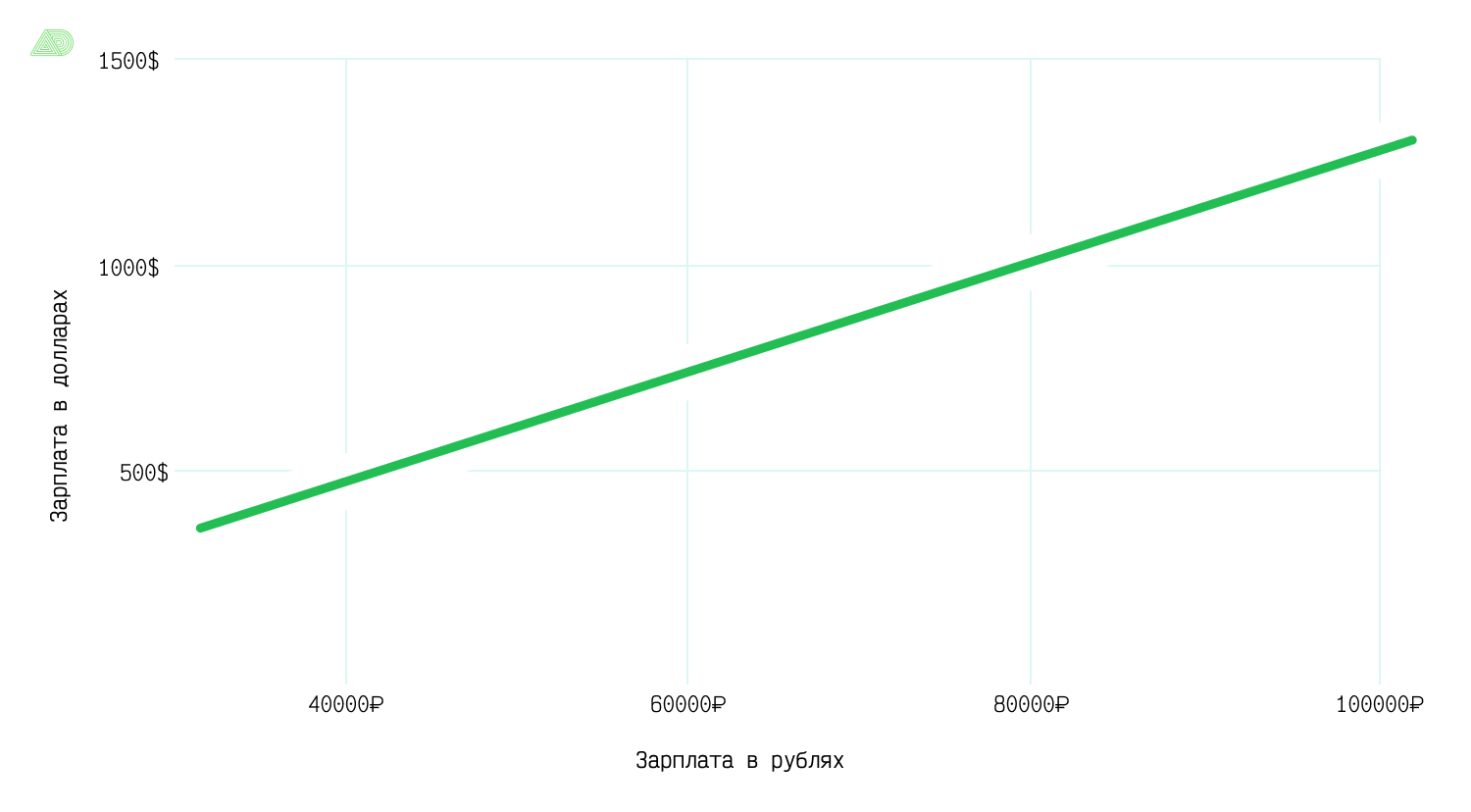
Но это редкий случай — на практике чаще встречаются признаки, коэффициент корреляции которых не равен единице, но достаточно велик и превышает (по абсолютной величине) пороговое значение, например, 0.7. Использование таких признаков также приведет к мультиколлинеарности.
Почему это плохо? Мультиколлинеарность негативно влияет на модели машинного обучения. Так, например, для линейных моделей она может приводить к неустойчивости коэффициентов.
Что это значит на практике? Разберемся на примере построенной нами поведенческой модели кредитного скоринга для Ак Барс Банка. Выдача кредита — это всегда риск невыполнения клиентом своих обязательств, поэтому банку важно оценивать ожидаемые потери. Они пропорциональны вероятности дефолта кредита — события, при котором клиент задержал выплаты по кредиту на 90 и более дней. Для предсказания дефолта потребительского кредита и была разработана наша модель.
Для модели скоринга важна интерпретируемость, то есть способность оценить влияние каждого из признаков на вероятность дефолта. Кроме того, для надежного предсказания вероятности, модель должна быть хорошо откалибрована. Исходя из этого мы выбрали модель логистической регрессии.
Модель построена на наборе признаков, описывающих договор и поведение клиента относительно выполнения обязательств по нему.
Пример признаков для описания кредитных договоров:
Количество месяцев с даты выдачи,
Длительность кредита отнесенная к сроку договора,
Количество действующих кредитов,
Количество месяцев с даты выдачи последнего кредита.
Пример признаков поведения клиента:
Отношение остатка долга к сумме данного кредита,
Количество просрочек,
Остаток долга по всем кредитам, отнесенный к сумме выдачи,
Количество просрочек от ... до ... дней в течение последних ... месяцев.
Всего в нашем распоряжении было 73 признака. Их первичный анализ показал наличие мультиколлинеарности.
Чтобы показать читателям негативное воздействие этого явления, мы обучили модель, используя сильно коррелированные признаки. Это привело к тому, что не все знаки коэффициентов модели соответствовали бизнес-логике.
Так, например, уменьшение значения признака «остаток долга / сумма выдачи» должно приводить к уменьшению вероятности дефолта, так как клиенту при этом остается выплачивать все меньшую сумму. Мультиколлинеарность привела к тому, что подобранный в ходе обучения модели коэффициент сменил знак на противоположный. А признак, с точки зрения модели, стал говорить об обратном: чем меньше остается платить, тем больше вероятность дефолта.
Такое поведение наблюдалось и для некоторых других признаков. Ну и, разумеется, построенную модель сложно интерпретировать. При этом у читателя может возникнуть вопрос: «а как же бороться с подобным влиянием мультиколлинеарности»? Попробуем ответить на него и опишем свою модификацию одного из популярных методов, которую мы использовали при отборе признаков для моделирования.
Что с этим делать?
Большинство методов устранения мультиколлинеарности предполагает исключение порождающих её признаков. Наиболее популярными среди них являются:
Исключение признаков по порогу на основе тепловой карты для коэффициентов корреляции. Метод не гарантирует исключение минимально возможного количества признаков. Выбор исключаемого признака, как правило, определен порядком их рассмотрения и не учитывает взаимосвязь с целевой переменной. Из-за этого можно потерять потенциально полезные признаки до этапа моделирования.
Исключение признаков на основе анализа VIF (variance inflation factor). Основной минус — неоднозначность выбора порога для исключения признака. Эмпирическое правило: выбираем порог из интервала 5—10.
Отбор признаков на основе анализа доли объясненной дисперсии для компонент, полученных PCA. Метод предполагает переход в новое признаковое пространство, что не всегда возможно для задач, где необходима интерпретируемость.
Нам лучше всего подходил первый метод, но нужно было как-то устранить его недостатки, поэтому мы решили модифицировать его.
Наш метод основан на алгоритме Брона-Кербоша — одном из алгоритмов решения задач теории графов о поиске максимальных клик. Клика — это такой подграф, в котором все вершины попарно соединены друг с другом. Например, граф, нарисованный в форме логотипа Ак Барс Банка, содержит 15 клик размера 2 (ребра графа), 6 клик размера 3, и одну клику размера 4.
Чтобы свести задачу к поиску максимальных клик, построим граф связей для признаков по таким правилам:
Каждая из вершин графа представляет собой отдельный признак,
Ребром соединяются только те вершины, которые не являются сильно коррелированными при заданном пороге корреляции.
Если для построенного графа мы сможем найти наибольшую клику, то это и будет решением нашей задачи. Алгоритм Брона-Кербоша находит все максимальные клики, при этом наибольших может быть несколько.
Здесь можно увидеть аналогию с социальной сетью, где пользователи — это признаки, а наличие связи между ними говорит о том, что они «дружат». При этом наличие «дружбы» зависит от некоторой величины, которую можно вычислить для каждой пары пользователей. Задача состоит в том, чтобы выделить сообщество, в котором каждый его участник «дружит» с остальными.
Как выделить оптимальную клику
Так как метод применяется для задачи бинарной классификации с количественными признаками, то в качестве меры, показывающей связь между признаком и таргетом, предлагается использовать совместную информацию (MI — mutual information).
Для двух клик одинаковой длины, будем считать лучшей ту, для которой сумма MI, вычисленная для всех признаков клики, наибольшая. Конечно, здесь может использоваться и любая другая релевантная решаемой задаче мера, например, вычисленная с использованием дисперсионного анализа (ANOVA).
Пошаговый алгоритм для описанного метода
Вычислить MI для всех признаков.
Вычислить матрицу корреляций.
Для заданного порога корреляции сформировать граф связей для признаков по описанным выше правилам.
Отыскать все максимальные клики для графа и выбрать одну или несколько наибольших.
На основании значений MI из шага 1 определить оптимальную клику.
Применение метода на практике
Мы запрограммировали алгоритм и проверили метод на модельной и реальной задачах классификации.
Модельная задача
Датасет сгенерирован при помощи функции make_classification библиотеки scikit-learn.
Основные характеристики датасета. Количество признаков равно семи, пять из них являются информативными (x_1–x_5), а x_6 и x_7 — случайная линейная комбинация информативных. В датасете 1000 записей. Баланс классов — 50/50.
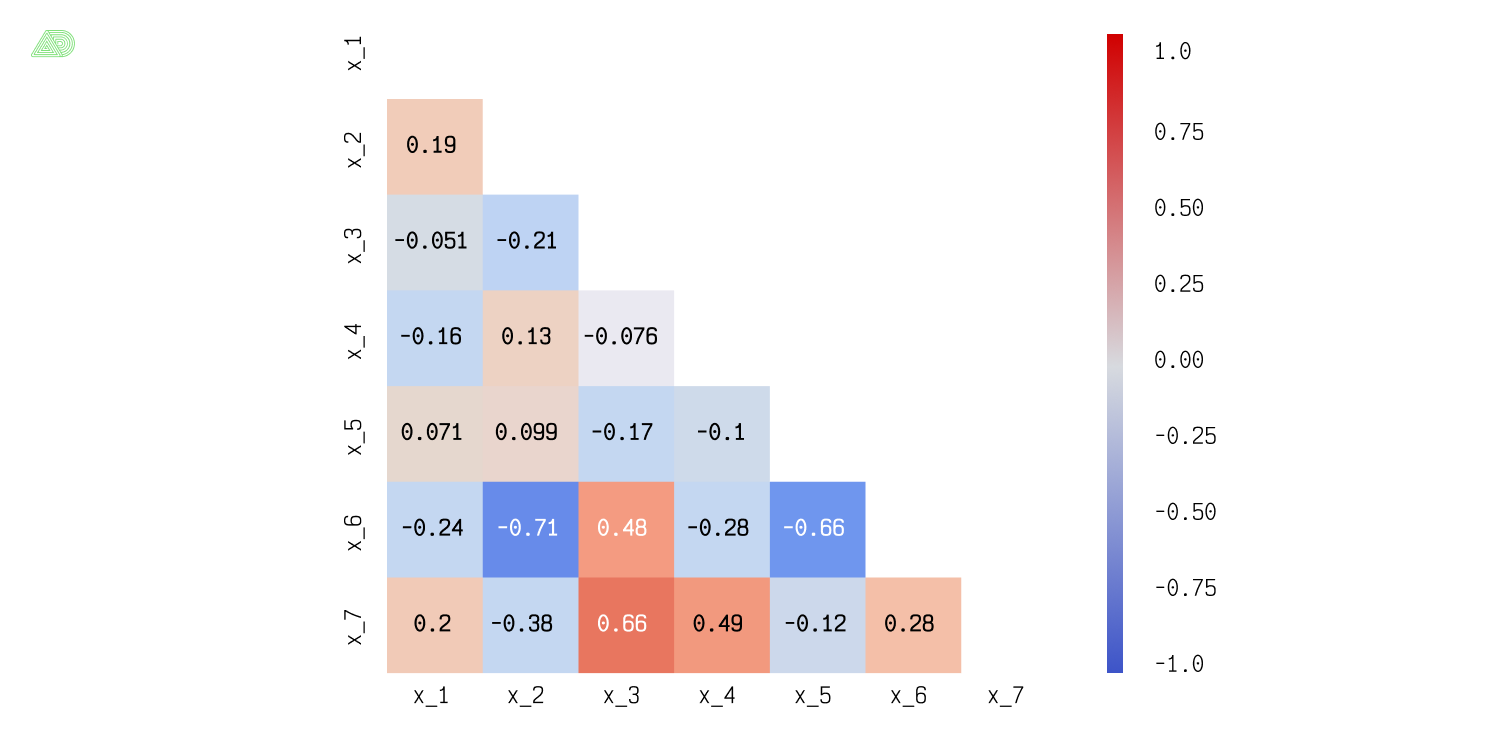
Тепловая карта корреляций признаков
Для выбранного нами порога 0.65, согласно тепловой карте корреляций признаков, сильно коррелированными будут пары (x_6, x_2), (x_6, x_5), (x_7, x_3). Внимательный читатель сможет сам отыскать в графе связей клику, например, {x_1 – x_5}.
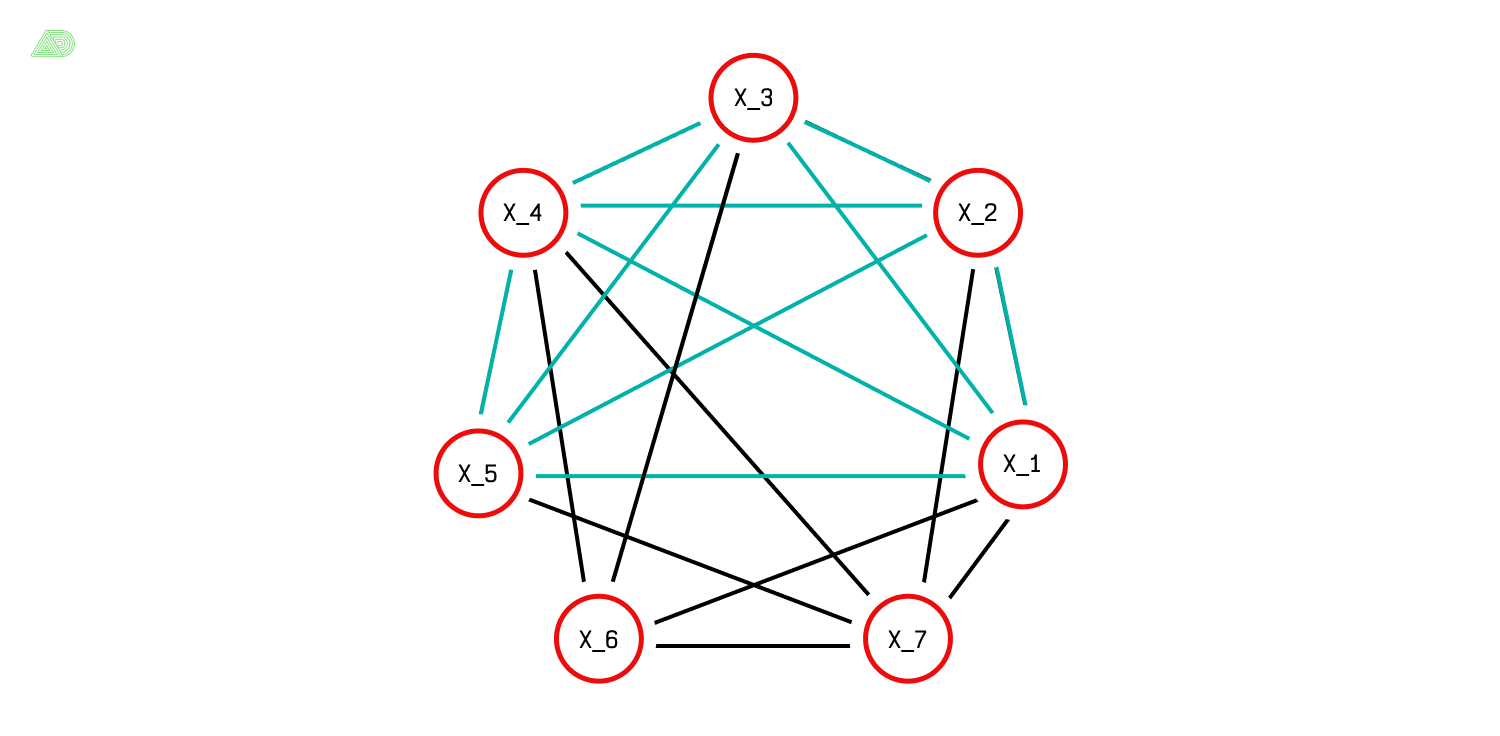
Граф связей для признаков модельной задачи
Алгоритм нашел две пары максимальных клик размера 4 и 5:
{x_1, x_4, x_6, x_7}и{x_1, x_3, x_4, x_6},{x_1, x_2, x_3, x_4, x_5}и{x_1, x_2, x_7, x_4, x_5}.
Наибольшими, очевидно, будут клики второй пары, для которых алгоритм выбрал оптимальную {x_1-x_5}, сравнив суммарный MI для обеих. Таким образом признаки x_6 и x_7 , которые порождали мультиколлинеарность, были исключены. Для отыскания максимальных клик использовалась реализация алгоритма Брона-Кербоша из библиотеки network-x.
Заинтересованному читателю, возможно, будет интересен документ с кодом для генерации данных и решения проблемы мультиколлинеарности в модельной задаче. В документе также представлена серия экспериментов по исследованию влияния мультиколлинеарности на коэффициенты модели, а также метрики ROC-AUC и f1-score. Приведем выводы, полученные в ходе проведения экспериментов:
Мультиколлинеарность приводит к неустойчивости коэффициентов логистической регрессии — коэффициенты могут менять свой знак при добавлении в модель новых признаков и становиться статистически незначимыми
С точки зрения метрик качество моделей не меняется:
ROC-AUC = 0.89,f1-score = 0.816
Реальная задача
Вернёмся, наконец, к тому, с чего начали — «боевой» задаче дефолта потребительского кредита. Мы не можем показать её решение столь же подробно, как сделали это для модельной, но приведем результаты работы нашего алгоритма.
На вход алгоритму отбора были поданы:
76000 записей для 73 признаков, определяющих поведение клиента и свойства самого договора кредитования, и целевая переменная,
Порог
0.8для определения степени корреляции признаков.
=> qliques search…
44335104 qliques are found:
29 14644224
30 11636736
28 8893440
31 5047296
27 2221056
32 1465344
33 254976
26 165888
34 6144
dtype: int64
Task completed in: 0:02:15.888461Вывод на печать результатов работы алгоритма: слева - размер найденных клик, справа — их количество
Алгоритму Брона-Кербоша удалось за 2 минуты 15 секунд отыскать примерно 44.3 миллиона максимальных клик. Размер найденных клик варьировался от 26 до 34, причем клик размера 34 было найдено 6144.
Для выбора оптимальной клики мы использовали значения MI, вычисленные на первом шаге. В результате была выделена единственная клика размера 34, признаки которой обладали следующими свойствами:
отсутствие мультиколлинеарности;
наибольший суммарный показатель MI среди всех клик размерности 34.
Это означало, что нам удалось расширить множество признаков, пригодных для построения модели. Для сравнения: применение подхода устранения мультиколлинеарности без предложенной модификации, приводило к отысканию всего лишь 23 признаков.
Нахождение максимального подмножества признаков позволило рассмотреть большее их количество для последующих этапов моделирования и способствовало построению более качественной модели: прирост метрики Average Precision составил 6%.
Рассмотренный метод устранения мультиколлинеарности может использоваться при работе с нелинейными моделями как способ снижения размерности признакового пространства.
Заключение
Итак, подытожим полученные результаты.
Для линейных моделей машинного обучения наличие мультиколлинеарности признаков может привести к неустойчивости коэффициентов — они могут изменять свой знак при добавлении в модель новых признаков и становиться статистически незначимыми, от чего страдает интерпретируемость модели.
Предложенный в статье метод устранения коллинеарности признаков позволяет отыскивать при заданном пороге корреляции подмножество признаков, обладающее следующими свойствами:
его размер максимален
входящие в него признаки не обладают свойством мультиколлинеарности, а также наилучшим образом (в смысле суммарного MI) описывают таргет
Применение модификации метода отбора признаков по порогу корреляции для реальной задачи поведенческого скоринга позволило построить хорошо интерпретируемую модель и улучшить значение метрики Average Precision на 6%.
Полезные ссылки:
Книга по регрессионному анализу: Understanding regression analysis
Статья на тему устранения мультиколлинеарности в линейных моделях
Статья на тему устранения мультиколлинеарности с использованием PCA
Статья, объясняющая что такое Mutual Information