В данной статье для реализации алгоритма будут рассмотрены:
Система хранения графа на основе List<>
Сортировка рёбер графа по весу
Система непересекающихся множеств
Алгоритм Краскала необходим для нахождения минимального остовного дерева графа.
О чём речь?
Если прочитав предложение выше вы невольно задались этим вопросом, то вам следует изучить пару книг по теории графов информацию, представленную в этом блоке.

На первом рисунке можно увидеть граф. Если мы соединим все его вершины без образования циклов, то получим остовное дерево этого графа. Примеры остовных деревьев выделены цветом на втором и третьем рисунках.
Теперь наделим рёбра нашего графа весом.

И речь уже будет идти о минимальном остовном дереве графа. Если мы имеем несколько вариантов остовных деревьев, минимальным из них будет считаться то, сумма веса всех рёбер которого меньше остальных.
На просторах интернета есть множество ресурсов, посвященных данному алгоритму, однако все варианты реализации, встреченные мной, показались слишком сложными для понимания и использования. Хочу предложить более приближенный к реальности вариант. Для удобства оставляю ссылку на репозиторий с полной реализацией и примерами.
План действий
Сортируем имеющиеся рёбра по весу.
Создаём новое множество и добавляем в него первое ребро.
Затем пытаемся добавить каждое новое ребро в имеющееся множество, если возникает цикл - пропускаем.
Итоговое множество рёбер и есть искомое минимальное остовное дерево.
По сути, это и есть формулировка алгоритма Краскала. Звучит совсем просто.
Самый весёлый пункт из имеющихся - третий. Потому что проверка на появление циклов на каждом шаге будет не сильно простым занятием. Его мы модифицируем при помощи системы непересекающихся множеств.
Но для начала давайте рассмотрим систему хранения графа в программе с использованием List<>. Если перед вами стоит задача неиспользования любых структур данных, кроме собственных, в этом репозитории вы найдёте нужную реализацию. Сам алгоритм в ней отличается незначительно.
Система хранения графа
Что есть граф? По сути - совокурность вершин и соединяющих их рёбер. Но ведь если помимо веса хранить о каждом ребре информацию о том, какие вершины оно соединяет, для помещения целого графа в память компьютера нам хватит списка рёбер, в него входящих.
Именно поэтому граф в этой реализации представлен дженерик листом рёбер.
Структура ребра и IComparable
Ниже можно увидеть структуру ребра: всё то, о чём было сказано выше. Вес и две вершины, представленные свойствами.
public class Edge : IComparable<Edge> { public int EdgeWeight { get; set; } public string VertexA { get; set; } public string VertexB { get; set; } public Edge(string vertexA, string vertexB, int weight) { VertexA = vertexA; VertexB = vertexB; EdgeWeight = weight; } public int CompareTo(Edge other) { if (other == null) return 1; return EdgeWeight.CompareTo(other.EdgeWeight); } }
Класс реализует интерфейс IComparable с целью упростить сортировку рёбер графа, а именно - не изобретать велосипед и просто использовать стандартную сортировку для листа.
Далее рассмотрим по частям класс Graph.
Структура и основные методы класса Graph
Для удобства работы он реализует IEnumerable<Edge>.
public class Graph : IEnumerable<Edge> { //код класса public IEnumerator<Edge> GetEnumerator() { return _graph.GetEnumerator(); } IEnumerator IEnumerable.GetEnumerator() { return _graph.GetEnumerator(); } }
В основе класса лежит List<Edge>, то есть список рёбер.
private List<Edge> _graph; public Graph() { _graph = new List<Edge>(); } public Graph(Edge val) { Edge[] value = new Edge[] { val }; _graph = new List<Edge>(value); }
Два конструктора облегчат работу с данным классом.
Далее можно увидеть несколько вспомогательных методов, таких как добавление в конец графа одного ребра и слияние графов. Последнему стоит уделить внимание.
Используя цикл foreach (да-да, именно для него нам пригодилась реализация интерфейса IEnumerable<Edge>) мы проходим по всем рёбрам второго графа и добавляем их к первому.
public void Add(Graph graph) { foreach (Edge edge in graph) { _graph.Add(edge); } } public void Add(Edge edge) { _graph.Add(edge); }
Это основа, но без неё никуда.
Перейдём к более важным для вывода информации методам класса.
public int GetWeight() { int weight = 0; foreach (Edge edge in _graph) { weight += edge.EdgeWeight; } return weight; }
Метод GetWeight() даёт нам возможность подсчёта суммарного веса графа.
public override string ToString() { string result = string.Empty; foreach (Edge edge in _graph) { result += $"{edge.VertexA} {edge.VertexB} {edge.EdgeWeight}\n"; } return result; }
Переопределяем метод ToString() мы с целью красивого вывода графа.
На этом базовые методы класса Graph заканчиваются.
Сортировка рёбер графа по весу.
А теперь приятный сюрприз. Всё, что нам нужно для сортировки рёбер по весу - эти четыре строчки.
public void Sort() { _graph.Sort(); }
Потому что класс рёбер реализует IComparable.
Система непересекающихся множеств
Данный вариант реализации далёк от оригинала, однако проще для восприятия.
Структура множеств
Каждое множество будет представлено классом Set с собственным графом и списком вершин, в оный входящих.

Отдельный лист вершин нужен нам для проверки на цикл в дальнейшем.
Переведём в код описанное выше:
public class Set { public Graph SetGraph; public List<string> Vertices; public Set(Edge edge) { SetGraph = new Graph(edge); Vertices = new List<string>(); Vertices.Add(edge.VertexA); Vertices.Add(edge.VertexB); } //методы класса }
Для работы с системой множеств нам понадобится ряд методов:
Объединение двух множеств, слияние. Здесь мы к имеющемуся множеству добавляем другое с использованием соединяющего ребра.
Добавление ребра к имеющемуся множеству.
Проверка наличия вершины в списке
Vertices.
public void Union(Set set, Edge connectingEdge) { SetGraph.Add(set.SetGraph); Vertices.AddRange(set.Vertices); SetGraph.Add(connectingEdge); } public void AddEdge(Edge edge) { SetGraph.Add(edge); Vertices.Add(edge.VertexA); Vertices.Add(edge.VertexB); } public bool Contains(string vertex) { return Vertices.Contains(vertex); }
Класс системы непересекающихся множеств
Рассмотрим класс, являющийся местом хранения всех имеющихся множеств и своего рода прослойкой, позволяющей добавить ребро в одно из множеств или решить, что оно никогда не займёт в них своё место.
class SystemOfDisjointSets { public List<Set> Sets; public void AddEdgeInSet(Edge edge) { //Здесь переданное ребро найдёт свое место в одном из множеств //или не войдёт в остовное дерево. } public Set Find(string vertex) { foreach (Set set in Sets) { if (set.Contains(vertex)) return set; } return null; } }
Метод Find принимает вершину графа и возвращает множество, к которому она принадлежит, или null, если такое множество не найдено.
Далее по шагам напишем метод public void AddEdgeInSet(Edge edge).
Разбиение графа на множества
Суть метода в том, что мы проходимся по всем рёбрам и проверяем, принадлежат ли стягиваемые ими вершины какому-либо множеству. Далее возможны четыре случая. Для наглядности изобразим их на схеме:
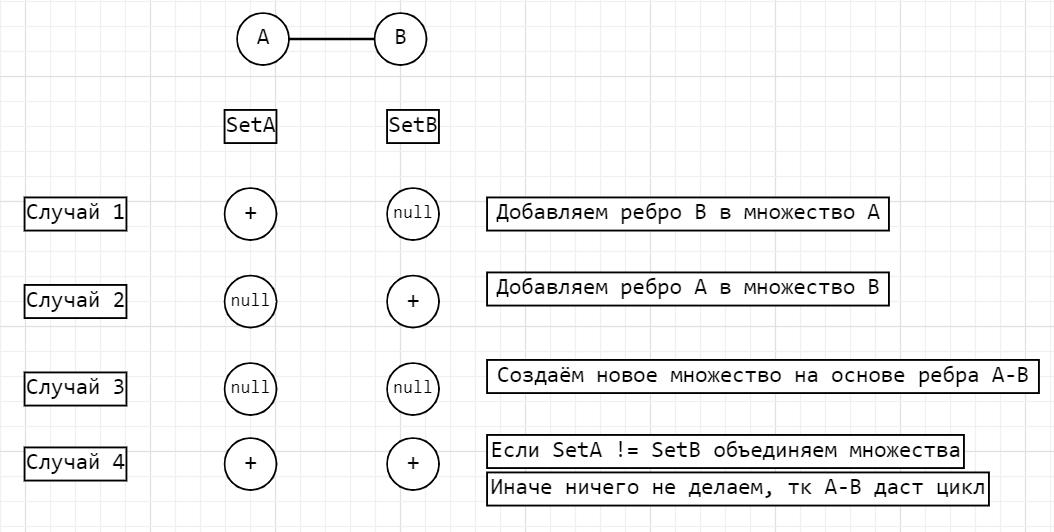
Осталось записать полученные варианты на С#:
public void AddEdgeInSet(Edge edge) { Set setA = Find(edge.VertexA); Set setB = Find(edge.VertexB); if (setA != null && setB == null) { setA.AddEdge(edge); } else if (setA == null && setB != null) { setB.AddEdge(edge); } else if (setA == null && setB == null) { Set set = new Set(edge); Sets.Add(set); } else if (setA != null && setB != null) { if (setA != setB) { setA.Union(setB, edge); Sets.Remove(setB); } } }
Алгоритм Краскала: объединим полученные механизмы
Теперь мы с чистой совестью можем записать алгоритм Краскала в классе Graph как метод FindMinimumSpanningTree.
Всё по пунктам, известным нам заранее:
Сортируем рёбра графа по возрастанию веса.
Используя систему непересекающихся множеств разбиваем граф на множества до тех пор, пока не останется лишь один Set. Он останется один гарантированно, если граф был связный.
Возвращаем минимальное остовное дерево, оно же - граф единственного оставшегося сета. (Для Find - using System.LINQ)
public Graph FindMinimumSpanningTree() { Sort(); var disjointSets = new SystemOfDisjointSets(); foreach (Edge edge in _graph) { disjointSets.AddEdgeInSet(edge); } return disjointSets.Sets.First().SetGraph; }
На этом алгоритм закончен, в репозитории также есть пример работы и удобного считывания графа из консоли, однако к теме статьи это не относится, поэтому не буду удлинять и без того обёмный текст.
Спасибо за внимание, надеюсь, что информация была полезной.
