Flammmable 16 мар 2022 в 19:51

Согласование импедансов: о пользе формул

17 мин

20K

Производство и разработка электроники*Электроника для начинающих

Согласование импедансов: как сломать и как починить
Согласование импедансов: симуляторы и симуляция. Часть 1
Согласование импедансов: симуляторы и симуляция. Часть 2
Согласование импедансов: переходные процессы и переходные отверстия
Согласование импедансов: о пользе формул

Данный цикл статей, начавшийся с практических измерений и чистой эмпирики, хотелось бы завершить рассмотрением некоторых теоретических аспектов, связанных с согласованием импедансов. А также рассмотреть их ценность (практическую, либо иную) с точки зрения любителя электроники, только что перешедшего от навесных проводов и Ардуино к чуть более быстрым микросхемам и устройствам.

Представим 50-омную линию, к которой подключен источник сигнала с внутренним сопротивлением 75 Ом, способный выдавать прямоугольные импульсы с амплитудой сигнала 10 вольт.

Кстати о термине «Амплитуда»

Стандарт «IEC60050 International electrotechnical vocabular», содержащий раздел №103 «Mathematics — Functions», определяет амплитуду, как «maximum value of a scalar sinusoidal quantity» и в качестве примера подчёркивает, что имеет ввиду множитель при косинусе. То есть согласно этому определению, амплитуда — это характеристика синусоиды и отсчитывается она от точки равновесия.

Однако раздел №702 «Oscillations, signals and related devices» данного стандарта содержит термин «Pulse magnitude», хотя и помеченный, как устаревший. Его определение: «a single value, for instance a mean, root mean square or peak value characterizing the aggregate instantaneous values of a unidirectional pulse with respect to the common initial and final value».

А действующий «ГОСТ 26.013-81 Средства измерения и автоматизации. Сигналы электрические с дискретным изменением параметров входные и выходные» определяет термин «Амплитуда сигнала», как «наибольшее значение, достигаемое напряжением (током) за время действия сигнала без учета выброса» и приводит картинку с прямоугольным импульсом и напряжением, принимаемым за амплитуду и измеренным от «подошвы» импульса до максимального его значения (исключая выброс).

В общем, если с амплитудой синусоиды всё понятно — она измеряется от точки равновесия и равна половине напряжения pick-to-pick, то амплитуды всех остальных сигналов пребывают если не в лингвистическом вакууме, то, по крайней мере, в несколько разреженном пространстве терминов.

Также, пускай сопротивление нагрузки будет равно 350 Омам. Просимулируем данную схему (например, в «MicroCap») и посмотрим на напряжения в различных точках линии.

Как видно, напряжения имеют подозрительно целые значения. Посчитаем их. В случае амплитуды сигнала, уходящего из источника в линию всё просто — эта амплитуда получается делением напряжения источника на воображаемом резистивном делителе. Верхняя часть этого делителя — внутреннее сопротивление источника, а нижняя — импеданс линии.

С отражением импульса всё несколько сложнее. Импульс, идущий по линии передачи и набегающий на высокоомную нагрузку можно сравнить с морской волной, ударяющейся об утес. В этой аналогии высота гребня — напряжение, а направление движения воды — ток. Если проследить за напряжением вблизи конца линии, то можно увидеть, что напряжения падающего и отраженного импульса имеют один знак. В тоже время токи падающего и отраженного импульса имеют противоположные знаки, так как ток падающего импульса направлен к нагрузке, а ток отраженного — от нагрузки.

Таким образом мы можем записать два уравнения:

$U^+{}+U^-{}=U_{load}$ $I^+{}-I^-{}=I_{load}$

Где U_load и I_load напряжение на приёмнике и ток через него, U⁺ и I⁺ напряжение и ток падающего импульса, U^- и I^-напряжение и ток отраженного импульса. Разделим одно уравнение на другое:

$\frac{U^+{}+U^-{}}{I^+{}-I^-{}}=\frac{U_{load}} {I_{load}}(1)$

Теперь вспомним закон Ома:

$I=\frac{U}{R}$

Или иначе говоря:

$R=\frac{U}{I}$

Преобразуем формулу (1):

$\frac{U^+{}+U^-{}}{I^+{}-I^-{}}=R_{load}$

Разделим обе части на Z₀ — волновое сопротивление:

$\frac{U^+{}+U^-{}}{Z_0{}I^+{}-Z_0{}I^-{}}=\frac{R_{load}} {Z_0}$

Еще раз обратимся к закону Ома:

В данном случае это соотношение справедливо будет и с волновым сопротивлением:

И у нас получается:

$\frac{U^+{}+U^-{}}{U^+{}-U^-{}}=\frac{R_{load}}{Z_0}$

Ряд скучных преобразований, по итогу которых мы...

Домножим на знаменатели:

$Z_0(U^+{}+U^-{})=R_{load}(U^+{}-U^-{})$

Раскроем скобки:

$Z_0 U^+{}+Z_0 U^-{}=R_{load} U^+{}-R_{load} U^-{}$

Сгруппируем амплитуды падающего и отраженного импульса:

$R_{load} U^-{}+Z_0 U^-{}=R_{load} U^+{}-Z_0 U^+{}$

Вынесем амплитуды за скобки:

$U^-{} (R_{load}+Z_0)=U^+{}(R_{load}-Z_0)$

Собираем напряжения с одной стороны, а сопротивления — с другой и...

…получим соотношение для вычисления т.н. коэффициента отражения:

$Г=\frac{U^-{}}{U^+{}}=\frac{R_{load}-Z_0}{R_{load}+Z_0}$

При амплитуде источника U_source=10 вольт, внутреннем сопротивлении источника R_source=75 ом и волновом сопротивлении линии Z₀=50 ом, падающий на нагрузку импульс будет иметь амплитуду:

$U^+{}=U_{source}{\frac{Z_0}{R_{source}+Z_0}}=10{\frac{50}{75+50}}=4В$

Если R_load=350 ом и Z₀=50 ом, то коэффициент отражения будет равен:

$Г=\frac{U^-{}}{U^+{}}=\frac{350-50}{350+50}=\frac{300}{400}=\frac3 4$

Следовательно U^-будет равно 3 вольтам, а U_load(напряжение на приёмнике) будет равно сумме напряжений падающего и отражённого импульсов, то есть 7 вольтам.

Как видно из формулы коэффициента отражения, он лежит в диапазоне от «-1» до «+1» и при отрицательных значениях коэффициента, напряжение отражённого импульса будет иметь знак, противоположный знаку напряжения падающего импульса.

Если говорить субъективно и претенциозно — формула коэффициента отражения и её вывод могут быть полезны в психологическом смысле. Они закрывают гештальт/создают инсайт: позволяют ощутить полное понимание процесса отражения сигнала от концов линии передачи. Также данное знание может поспособствовать успешной сдаче зачёта/экзамена/курсовой в ВУЗе. Возможно, оно также будет полезно, если любитель из мира цифровых микросхем захочет прикоснуться к магии РЧ/СВЧ. В практическом же смысле, вероятность того, что придётся в явном виде подставлять какие-либо значения в эту формулу, занимаясь трассировкой печатной платы, скажем, с микроконтроллером STM32F779 и динамической памятью MT48LC4M16A2 (частоты работы данной связки микросхем — около 100МГц), близка к нулю. Причины тому — широкий выбор различных симуляторов; отсутствие в большинстве подобных случаев значения сопротивления нагрузки, как единственного числа — в неявном виде оно представлено в табличной форме в моделях входных буферов, используемых в симуляторах; а также отсутствия точных аналитических формул для расчёта волнового сопротивления дорожек печатных плат.

КСВ

Если у нас имеются конкретные значения сопротивления нагрузки и импеданса линии, то мы сможем посчитать коэффициент отражения по формуле и далее вычислить все возможные напряжения в различных точках линии. Но представим, что у нас есть установка с заранее не вполне точно известными параметрами и мы хотим измерить, насколько хорошо нагрузка согласована с линией.

Представим также, что измерить уровень согласования нужно максимально точно и с минимальными финансовыми затратами. И при всём этом, мы с вами являемся попаданцами в дизельпанк 1930-х годов — без симуляторов, векторных анализаторов и «заряженных» цифровых осциллографов. Как нам следовало бы поступить при таких начальных условиях?

Есть физический эффект, который сильно помог бы нам. Пускай у нас есть источник синусоидального сигнал постоянной частоты, фазы и амплитуды. Этот сигнал, отражаясь от несогласованной нагрузки будет возвращаться обратно в линию. В каждой точке линии, в каждый момент времени напряжение будет равно сумме напряжений падающего и отраженного сигналов в этой точке. Так как эти два сигнала движутся по линии навстречу друг другу, а также имеют одну частоту, то в линии будут фиксированные точки, где падающий и отраженный сигналы будут усиливать друг друга. А также будут точки, где они будут взаимоослабляться. То есть образуется так называемая стоячая волна.

Для анимации этой GIF надо щёлкнуть по ней

При максимально несогласованной нагрузке синусоидальный сигнал будет отражаться полностью. И в пучностях (точках сложения амплитуд) амплитуда колебания напряжения будет равна двойной амплитуде падающего сигнала. А в узлах (точках взаимоослабления) колебаний не будет вовсе. При полностью согласованной нагрузке отраженного сигнала не будет, нечему будет складываться и амплитуда колебаний по всей длине линии будет одинакова и равна одной амплитуде падающего сигнала. При частично согласованной нагрузке, в пучностях амплитуда колебаний будет несколько меньше удвоенной амплитуды падающего сигнала, а в узлах — чуть больше нуля. Таким образом, отношение между амплитудой колебаний напряжения в пучности и в узле показывает степень согласования нагрузки с линией передачи.

Данное соотношение называется коэффициентом стоячей волны (КСВ). Запишем его определение в виде формулы:

$\frac{U^+{}+ |U^-{}|} {U^+{}- |U^-{} |} =КСВ$

Вспомним про коэффициент отражения:

$ГU^+{}=U^-{}$

И подставим это выражение в формулу КСВ:

$\frac{U^+{}+ |ГU^+{}|}{U^+{}- |ГU^+{} | } =КСВ$

Вынесем множитель U⁺ из числителя и знаменателя, а затем сократим его:

$\frac{1+ |Г|} {1- |Г|} =КСВ$

И после недолгих преобразований получим:

$|Г|=\frac{КСВ+1} {КСВ-1}$

Но как найти узлы и пучности, скажем, на центральной жиле коаксиального кабеля, а также измерить колебания напряжения на ней? Ведь снаружи центральной жили расположен диэлектрик, а поверх него — экран из фольги. Для этого подойдёт полностью механическое и, соответственно, доступное в 1930-е годы устройство — измерительная линия! По сути, это отрезок коаксиальной линии у которого в качестве диэлектрика используется воздух и имеется длинная прорезь вдоль экрана. В эту прорезь помещён зонд, не касающийся центральной жилы.

Измерительную линию подключают между источником сигнала и нагрузкой. Затем подают сигнал и настраивают контур зондовой головки так, чтобы измеряемые значения стали максимальными. Затем перемещают зонд вдоль центральной жилы, обнаруживают узлы и пучности стоячей волны, и, поделив измеренную амплитуду колебаний в пучности на амплитуду колебаний в узле получают значение КСВ.

Кстати о «щелевых» терминах в электронике

В англоязычной терминологии измерительная линия называется «slotted line». Данный термин очень хочется перевести, как «щелевая линия». Однако термин «щелевая линия» относится к совсем другому объекту. Это такая линия передачи, у которой сигнал подводится к обширному полигону, рассечённый узким вырезом (щелью), а затем распространяется вдоль этой щели. И данный термин переводится на английский язык, как «slot line». Также имеется особый типе антенн — щелевые антенны («slot antenna») — который в ряде случаев представляет из себя волновод с проделанными в нём щелями. Это всё — разные вещи :)

Получив значение КСВ, его можно даже не пересчитывать в коэффициент отражения. Если КСВ близок к единице — согласование отличное. Если он измеряется десятками, сотнями или тысячами — всё очень плохо. Также, прямо в КСВ можно нормировать согласование, указывая его значение в технической документации. Вот, к примеру, документация на антенну ANT-GHEL2R-SMA, в которой указан параметр VSWR (КСВН).

Есть, правда, один важный момент. В электронике существует целый класс устройств под общим названием «направленные ответвители». Некоторые из этих устройств способны разделить падающий и отражённый сигналы по отдельным каналам, что позволяет измерить их амплитуды непосредственно.

Естественно, направленные ответвители в той или иной форме пытались адаптировать для измерения отражений в линии и уровня согласования. Так, ещё в 1959 году, в апрельском номере журнала «QST» (одном из старейших журналов о любительской радиосвязи) была опубликована статья «An Inside Picture of Directional Wattmeters», в которой приводилась схема, по сути, КСВ-метра на двух диодах, позволяющая непосредственно сравнивать амплитуды падающего и отраженного сигналов.

Иными словами, коэффициент отражения по измеренным на КСВ-метре значениям, еще 60 лет назад было вычислять чуть проще, чем по тем же значениям вычислять сам КСВ. Помимо того, что в КСВ-метрах на основе направленных ответвителей нет подвижных частей и погрешностей, связанных с механическими перемещениями, важным фактором является 60-летний прогресс в производстве печатных плат и электронных компонентов. Который привел к тому, что применение измерительных линии в настоящее время крайне экзотическое мероприятие.

Причина, по которой КСВ до сих пор применяется при нормировании уровня согласования антенн приблизительно та же, что и причина, по которой фут в ряде стран остаётся актуальной единицей длины — согласование самых первых антенн измерялось именно в КСВ и тех пор это стало традицией.

Если говорить субъективно и претенциозно — КСВ будет невероятно полезной и актуальной для вас величиной... если вы 25-летний специалист по радиотехнике, рождённый в 1910 году. Измерение же КСВ дорожки, которая соединяет, к примеру, микросхему ПЛИС с микросхемой динамической памяти — действие, трудновыполнимое на практике и крайне странное на уровне идеи.

Волновое сопротивление

Предположим, у вас есть источник синусоидальных колебаний амплитудой U_max. Пускай у данного источника имеется внутреннее сопротивление r. Амплитуда синусоидального тока при коротком замыкании данного источника будет равна:

$I_{max}=\frac{U_{max}}{r}$

Теперь представим, что у нас имеется колебательный контур без потерь, которому сообщили некоторую энергию, путём создания на обкладках конденсатора напряжения U_max при нулевом токе через индуктивность. Колебания тока и напряжения будут также синусоидальными. Но, в отличие от предыдущего случая, они будут смещены на 90°, так как энергия будет периодически скапливаться то в конденсаторе, то в индуктивности. Максимальная энергия конденсатора будет равна:

${W_{max}}=\frac{C U_{max}^2}{2}$

Максимальная энергия в катушке индуктивности будет равна:

$W_{max}=\frac{LI_{max}^2}{2}$

Найдём соотношение между амплитудой колебаний напряжения и амплитудой колебаний тока в колебательном контуре. Для этого приравняем энергии:

$\frac{LI_{max}^2}{2}=\frac{CU_{max}^2}{2}$

Домножим на два левую и правую часть:

${LI_{max}^2}={CU_{max}^2}$

Оставим слева только квадрат тока:

$I_{max}^2=\frac{U_{max}^2} { L/C }$

Извлечём корень из левой и правой части:

$I_{max}=\frac{U_{max}} { \sqrt{L/C} }$

Таким образом для заряженного колебательного контура мы получаем некий аналог внутреннего сопротивления:

${Z_0}=\sqrt{\frac{L} {C}}$

Теперь предположим, что мы хотим, чтобы колебательный контур максимально быстро отдал накопленную в нём энергию. Для этого присоединим к нему резистор. Какой номинал резистора разрядит контур максимально быстро?

Если номинал будет велик, то мы получим почти тот же самый колебательный контур. Если номинал будет близок к нулю, то ток из катушки индуктивности будет долго-долго течь по ней и по короткому замыканию в обход конденсатора. Очевидно, между нулём и бесконечностью есть некий максимум.

Оставим на некоторое время колебательный контур и вернёмся к источнику напряжения U с внутренним сопротивлением Z₀. Определим такое значение нагрузки R_load при котором источник начнёт передавать нагрузке энергию максимально быстро, то есть будет сообщать её максимальную мощность.

При большом R_load ток источника будет мал и мощность будет также мала. При малом R_load ток будет большой, но бо́льшая часть мощности будет выделяться внутри источника. Выведем зависимость мощности, сообщаемой нагрузке от её сопротивления. В целом, мощность равна произведению тока на напряжение:

${P_{load}}= I_{load}U_{load}$

Ток через нагрузку равен общему току в цепи:

${I_{load}}=\frac{U}{{Z_{0}}+{R_{load}}}$

Напряжение на нагрузке получается делением номинального напряжения источника на резистивном делителе, где нагрузка — это нижний резистор:

$U_{load}=U \frac{R_{load}}{Z_{0}+R_{load}}$

Таким образом получается выражение для мощности:

$P_{load}=U^2 \frac{R_{load}} {(Z_{0}+R_{load})^2}$

Вспомним, что максимумы или минимумы функции находятся в тех точках, где её производная равна нулю (с известными оговорками). Поэтому возьмём производную от P_load_. Но сначала вспомним формулу производной отношения двух функций:

$(\frac{u}{v})'=\frac{(u'v-v'u)}{v^2}$

Итак. Выносим константу U² и применяем формулу для производной:

$P_{load}'=U^2 \frac{{R_{load}'}(Z_{0}+R_{load})^2-R_{load}((Z_{0}+R_{load})^2)'}{((Z_{0}+R_{load})^2)^2}$

Обратить всё выражение в ноль может только числитель дроби. Поэтому перепишем его и приравняем к нулю:

${R_{load}'}(Z_{0}+R_{load})^2-R_{load}((Z_{0}+R_{load})^2)'=0$

Берём производные:

$(Z_{0}+R_{load})^2-2R_{load}(Z_{0}+R_{load})=0$

Раскрываем скобки:

$Z_{0}^2+2Z_{0}R_{load}+R_{load}^2-2R_{load}Z_{0}-2R_{load}^2=0$

Упрощаем выражение:

$Z_{0}^2-R_{load}^2=0$

Готово:

$Z_{0}=R_{load}$

Мощность, передаваемая нагрузке будет максимальна тогда, когда сопротивление нагрузки будет равно внутреннему сопротивлению источника. И точно также, максимально быстро энергию из колебательного контура извлечёт резистор, сопротивление которого равно Z₀, либо… другой незаряженный колебательный контур с импедансом Z₀.

Данные выкладки не столько доказывают, сколько показывают приблизительное направление рассуждений, позволяющих вывести формулу волнового сопротивления длинной линии без потерь (являющейся, по сути, цепочкой колебательных контуров):

${Z_{0}}= \sqrt{\frac{L}{C}}$

...где L — погонная индуктивность, а C — погонная ёмкость линии. Строгий вывод данного соотношения (а также соотношения для линии с потерями) несколько более объёмен и непосредственно связан с так называемыми «Телеграфными уравнениями».

Попробуем вывести аналитические выражения для погонной индуктивности и ёмкости коаксиального кабеля для того, чтобы потом получить аналитическую формулу для вычисления его импеданса.

Прежде чем искать индуктивность кабеля, обсудим несколько понятий и терминов, относящихся к магнитному полю проводников с током. Магнитное поле в каждой точке пространства характеризуется вектором магнитной индукции. Если вокруг проводника с током провести такую замкнутую линию, что вектор магнитной индукции в каждой её точке будет направлен по касательной к ней, то такая линия будет называться силовой линией. Представим себе механическую аналогию: вокруг проводника с током проведена железная дорога, по которой без трения по инерции движется состав из вагонеток. Вектор импульса каждой вагонетки, проходящей через определённую точку — это, условно, вектор магнитной индукции, а сама железная дорога — это силовая линия.

Существует такое важное понятие, которое пригодится нам в дальнейшем, как циркуляция вектора. Применительно к нашей механической аналогии — это совокупный импульс всего состава, движущегося по силовой линии (строго говоря, по любой замкнутой линии и с рядом оговорок, но рассматриваемые нами линии будут совпадать с силовыми). Если мы точно знаем, что рассматриваемая нами силовая линия имеет форму окружности, которая лежит в плоскости, перпендикулярной оси проводника и с центром на этой оси, рассматриваемое нами пространство однородно и, следовательно, в каждой точке силовой линии модуль вектора магнитной индукции одинаковый, то для нахождения циркуляции нам нужно всего лишь умножить магнитную индукцию в точке на длину окружности радиуса r. То есть:

${rot \bar B }= 2 \pi rB$

Существует «Теорема о циркуляции магнитного поля», из которой следует, что циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна суммарному току, пронизывающему этот контур. Для меди, алюминия, золота, а также текстолита, воздуха, вакуума, фторопласта, полиэтилена и многих других материалов, коэффициентом пропорциональности является магнитная постоянная μ₀ (относительная магнитная проницаемость μ для данных сред очень близка к единице). То есть:

${rot \bar B }= μ_{0}I$

Приравняем выражения:

$2 \pi rB= μ_{0}I$

...и выведем уравнение для нахождения модуля вектора магнитной индукции в точке на расстоянии r от проводника:

$B= \frac{μ_{0}I}{2 \pi r}$

Данное выражение подходит для случая бесконечно тонкого и бесконечно длинного провода. Попробуем найти закономерность для сплошного цилиндрического проводника ненулевого диаметра, а также проводника в виде трубки.

Предположим, что ток в толще сплошного цилиндрического проводника равномерен. Тогда если мы возьмём силовую линию (контур) радиусом r внутри самого проводника, то ток сквозь данный контур будет равен:

$I_{внутр}= I \frac{\pi r^{2}} {\pi R^{2}}$

И магнитная индукция внутри проводника будет равна:

$B_{внутр}= \frac{μ_{0}}{2 \pi r}I\frac{r^{2}} {R^{2}}=\frac{μ_{0}Ir}{2 \pi R^{2}}$

То есть с ростом расстояния от оси магнитная индукция будет линейно нарастать до поверхности проводника. Однако дальше ток, охватываемый силовой линией перестанет расти (зафиксировавшись на отметке I) и магнитная индукция начнёт уменьшаться, аналогично случаю с проводом бесконечно малого диаметра.

В случае, если проводником является полая трубка, магнитное поле внутри неё будет отсутствовать, так как контуры, прокладываемые внутри трубки не охватывают никакой ток. Начиная с поверхности трубки, силовые линии будут охватывать ток I. Соответственно, поле будет иметь такие же параметры, как в случае бесконечно тонкого провода или цилиндрического проводника с тем же током и тем же (либо меньшем) радиусом.

В случае коаксиального кабеля возвратный ток будет двигаться по экрану — цилиндрическому проводнику. Прямой ток, ввиду скин-эффекта также будет идти по преимущественно по поверхности центральной жилы. То есть мы имеем суперпозицию полей двух вложенных друг в друга трубчатых проводников.

Внутри центральной жилы магнитное поле экрана будет отсутствовать полностью, а магнитное поле центральной жилы будет тем меньше, чем более выражен будет скин-эффект. Вне коаксиального кабеля и экран и центральная жила будут создавать такое же поле, как у бесконечно тонкого проводника. Но так как ток в проводнике и экране одинаков по силе и противоположен по направлению, то суммарное магнитное поле вне коаксиальной линии будет равно нулю. Таким образом, всё магнитное поле внутри линии будет расположено между поверхностью центральной жилы и экраном. Причём магнитная индукция этого поля будет такая же, как у бесконечно тонкого проводника с током I.

Выше уже приводилась формула, связывающая энергию магнитного поля с индуктивностью и силой тока:

$W= \frac{LI^{2}} {2}$

Используя данную формулу и зная энергию магнитного поля и силу тока, можно найти индуктивность:

$\frac{2W} {I^2}=L$

Энергию магнитного поля также можно вычислить, если известна плотность энергии магнитного поля, которая равна:

$ω= \frac{B^{2}} {2 μ _0}$

Подставляя найденное ранее значение магнитной индукции в данную формулу, мы получим:

$ω= ({\frac{μ_{0}I}{2 \pi r}})^2/2μ_{0}=\frac{μ_{0}I^2} {8 \pi ^2 r^2}$

Для вычисления энергии магнитного поля в кабеле нужно просуммировать плотность энергии во всех точках, где есть это поле. То есть проинтегрировать плотность энергии по объёму. Но так как нас интересует погонная индуктивность, а не индуктивность всей линии, то и интегрировать нам нужно будет лишь кольцо единичной высоты. Для начала посчитаем энергию одной круговой силовой линии просто умножив плотность энергии в каждой точке линии на длину этой линии:

$dW=ω2 \pi r=\frac{μ_{0}I^2} {8 \pi ^2 r^2}2\pi r=\frac{μ_{0}I^2} {4 \pi r}$

А затем проинтегрируем энергию всех силовых линий от центральной жилы до экрана:

$W=\int_{R_{жилы}}^{R_{экрана}} \frac{μ_{0}I^2}{4 \pi r} {dr}$

Так как все переменные не зависят от r, то они в данном случае являются константами и их можно вынести из-под интеграла. Под интегралом останется выражение 1/r, первообразная которого является натуральным логарифмом:

$W= \frac{μ_{0}I^2} {4 \pi} \int_{R_{жилы}}^{R_{экрана}}{\frac {dr}{r}}={\frac{μ_{0}I^2}{4 \pi}}(ln(R_{экрана})-ln(R_{жилы}))$

Разность логарифмов можно преобразовывать в отношение их аргументов:

$W= {\frac{μ_{0}I^2}{4 \pi }}ln(\frac{R_{экрана}}{R_{жилы}})$

И подставляя значение энергии в формулу для индуктивности, мы найдём зависимость погонной индуктивности от радиусов экрана и центральной жилы:

$L=\frac{2W}{I^2}={\frac{μ_0}{2 \pi}}ln(\frac{R_{экрана}} {R_{жилы}})$

Теперь определим ёмкость коаксиальной линии

Коаксиальная линия является, по сути, цилиндрическим конденсатором. Для определения ёмкости коаксиальной линии нам пригодится такое понятие, как поток вектора. Говоря крайне условно, для нашего случая, поток вектора через поверхность — это количество силовых линий, пронизывающих эту самую поверхность под прямым углом. Если во всех точках поверхности модуль вектора напряжённости одинаковый и направлен перпендикулярно поверхности, то поток через данную поверхность будет произведением модуля вектора напряжённости на площадь:

$Ф_E= {ES}$

Площадь поверхности цилиндра равна длине окружности, умноженной на высоту цилиндра, но так как мы рассматриваем погонную величину, то нас интересует участок единичной высоты.

Итак, поток через соосную цилиндрическую поверхность между центральной жилой и экраном с радиусом r будет равен:

$Ф_E= {E2 \pi r}$

С другой стороны, по теореме Гаусса, поток вектора напряжённости электрического поля Ф_E через замкнутую поверхность (то есть некую оболочку), пропорционален заряду внутри этой поверхности. Коэффициентом пропорциональности выступает электрическая постоянная ε₀ ,а так же диэлектрическая проницаемость среды ε:

$Ф_E= \frac{q} {εε_0}$

Боковая поверхность цилиндра, строго говоря, не является замкнутой оболочкой, но если рассматривается бесконечно длинный цилиндр, то отсутствие/наличие торцов становится не существенно. Поэтому приравнивая два выражения для потока получаем:

${E2 \pi r} = \frac{q} {εε_0}$

То есть напряжённость электрического поля между центральной жилой и экраном на расстоянии r от общей оси будет равна:

${E} = \frac{q} {εε_0 2 \pi r}$

Плотность энергии в точке, где напряжённость электрического поля равно E вычисляется по формуле:

${ω}= {\frac{εε_0 E^{2}}{2}}$

Подставляя в формулу плотности энергии выражение для напряжённости электрического поля, мы получим следующее:

$ω= \frac{q^{2}} {εε_0 8 \pi ^2 r^2}$

Если мы выберем воображаемую окружность радиуса r, соосную кабелю и находящуюся между центральной жилой и экраном, то совокупная энергия электрического поля этой окружности будет равна:

$dW= ω2\pi r=\frac{q^{2}} {εε_0 8 \pi ^2 r^2} 2\pi r=\frac{q^{2}} {εε_0 4 \pi r}$

Проинтегрируем (просуммируем) энергию таких окружностей от самой поверхности центральной жилы до экраны, что бы узнать энергию всего кольца:

$W= \int_{R_{жилы}}^{R_{экрана}}{\frac{q^{2}} {εε_0 4 \pi r}}dr={\frac{q^{2}} {εε_0 4 %pi r}} \int_{R_{жилы}}^{R_{экрана}}{\frac{dr} {r}}$

Взяв данный определённый интеграл мы получим:

$W= {\frac{q^{2}} {εε_0 4 \pi r}}ln(\frac{R_{экрана}}{R_{жилы}})$

Зависимость энергии конденсатора от его ёмкости и заряда определяется уже упоминавшемся выражением:

$W=\frac{CU^2} {2}$

Так как заряд на обкладках конденсатора пропорционален напряжению, причём коэффициент пропорциональности — это ёмкость, то можно сказать, что:

$U=\frac q C$

И, соответственно:

$W=\frac{q^2} {2C}$

Таким образом, ёмкость конденсатора будет равна:

$C=\frac{q^2} {2W}$

Подставим в эту формулу выведенное выше выражение для энергии электрического поля и получим…

$C=\frac{2 \pi εε_0} {ln(\frac{R_{экрана}}{R_{жилы}})}$

Подставляя выражения погонной индуктивности и погонной ёмкости в формулу для волнового сопротивления, мы получим следующее:

${Z_{0}}=\sqrt{\frac L C}=\sqrt{\frac{μ_0}{4 \pi ^2 εε_0}}ln(\frac{R_{экрана}}{R_{жилы}})$

Если подставить все константы, то коэффициент будет почти «круглым»:

${Z_{0}}= {\frac{59,9585} {\sqrt{ε}}}ln(\frac{R_{экрана}}{R_{жилы}})≈{\frac{60}{ \sqrt{ε}}}ln(\frac{R_{экрана}}{R_{жилы}})$

Как тут не вспомнить шутку с xkcd

Ещё я слышал, что корень четвёртой степени из (9^2 + 19^2/22) равен пи

Ссылка на русскоязычный оригинал.

Посмотрим, однако, на следующую иллюстрацию:

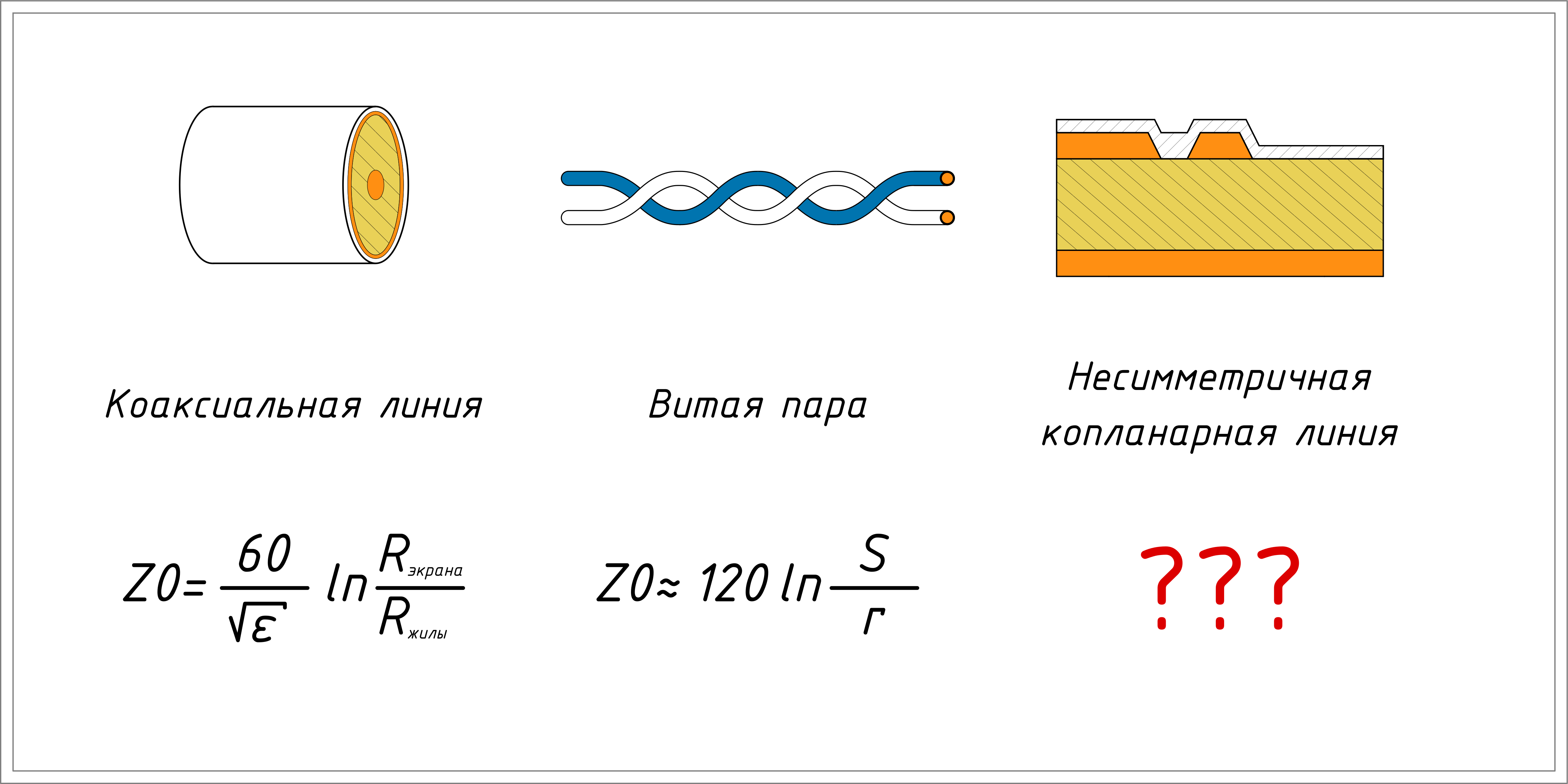
Здесь может сразу возникнуть пара вопросов:

Насколько сильно отличается волновое сопротивление пары параллельных проводников от реальной витой пары — скрученной и в оболочке?
По какой формуле считать погонную индуктивность и ёмкость несимметричной копланарной линии с конформной маской?

Проблема в том, что чем сильнее линия отличается от какого-либо симметричного и типового случая, тем более аналитическая формула для вычисления волнового сопротивления такой линии будет обрастать дополнительными условиями и ограничениями. В конечном итоге подобные формулы для реальных дорожек на плате, либо сильно теряют в точности, либо перестают быть чисто аналитическими и становятся полуэмпирической подгонкой под результат. При этом численные методы, при вполне допустимом затрачиваемом времени, показывают погрешность существенно меньше, чем подобные полуэмпирические формулы.

Если говорить субъективно и претенциозно — с практической точки зрения, инженер, умеющий выводить уравнение волнового сопротивления длинной линии, сможет вычислять это самое волновое сопротивление для дорожек на печатной плате либо столь же быстро и точно, либо медленнее и грубее, чем инженер не умеющий его выводить, но обладающий продвинутым калькулятором импеданса. Причём это «столь же» случится ровно тогда, когда первый инженер также получит в распоряжение продвинутый калькулятор.

Если же говорить об инженере, который сам пишет калькулятор импеданса, то следует обратить внимание на хабростатью «Написание МКЭ расчетчика в менее чем 180 строк кода» с применением метода конечных элементов для анализа механических деформаций и напряжений. Даже по столь учебному примеру видно, что знание одних телеграфных уравнений — это лишь малая часть необходимого бэкграунда для создания качественного калькулятора импеданса.

Можно предположить, что вывод формулы волнового сопротивления позволит обрести инженеру некое понимание и интуицию. Например, он будет знать, что увеличив толщину платы с микрополоском, он уменьшит погонную ёмкость линии, так как ёмкость плоского конденсатора равна:

$C= \frac{εε_{0}S} {h}$

И, помня о формуле...

${Z_{0}}= \sqrt{\frac{L} {C}}$

...он увеличит, тем самым, волновое сопротивление. Однако количество физических параметров копланарной линии в зависимости от детализации составляет всего от 5 до 8 штук. Ввод этих параметров в калькулятор, а затем изменение по очереди каждого из них (с целью понимания степени влияния на волновое сопротивление) займёт кратно меньше времени, чем вывод формул. Уровень же развития инженерной интуиции при этом будет приблизительно одинаков.

Наконец, можно предположить, что формула волнового сопротивления окажется полезной при измерении волнового сопротивления, скажем, коаксиального кабеля — с измерением параметров L и С. Однако раздел №7 стандарта «ГОСТ 27893-88 Кабели связи. Методы испытаний» предписывает присоединить к измеряемому кабелю с одной источник сигналов с измерителем отражений, а с другой — переменную нагрузку. И изменять её значение до тех пор, пока отражения не станут минимальны. Так, пункт 7.3.4 данного стандарта прямо сообщает «Волновое сопротивление отсчитывают по настроенному на испытуемый кабель нагрузочному контуру». То есть измерение волнового сопротивления осуществляется прямым методом, минуя измерения L и C.

Поэтому ценность соотношения...

${Z_{0}}= \sqrt{\frac{L} {C}}$

...видится далеко не абсолютной.

Заключение

Согласование импедансов в контексте обеспечения целостности сигнала не является герметично изолированным разделом электроники, так что технически, данный цикл можно было бы продолжить и осветить вопросы:

Из чего состоят модели IBIS и IBIS-AMI? Как их сделать своими руками, в том числе, по имеющейся микросхеме?
Что такое диаграмма Смита и S-параметры, почему их так часто упоминают в контексте согласования импедансов, когда знание данных понятий может быть полезным и в каком случае оно окажется бесполезным?
Как устроены приёмники и передатчики дифференциальных сигналов? Как проводить дорожки для этих сигналов (дифференциальные пары) и как согласовывать эти дифференциальные пары?

Однако, в то же время, ответы на вышеуказанные вопросы содержат в себе значительный объём информации из смежных разделов, достаточно сильно отходя от первоначальных задач данного цикла, вроде ответа на вопрос «как избавиться от «звона» в моём SPI?».

Выражаю надежду, что:

мне удалось в достаточной мере осветить понятие «Согласование импедансов» для тех, кто совсем недавно столкнулся с необходимостью обеспечения целостности сигналов.
мне удастся когда-нибудь рассказать и о смежных темах.

Большое спасибо за то, что дочитали! :)

Теги:

Хабы:

Согласование импедансов: о пользе формул

КСВ

Волновое сопротивление

Заключение

Публикации

Истории

Ближайшие события