Всем привет! Меня зовут Пантелеев Александр и я бэкенд-разработчик в компании Bimeister.

Постараюсь описать исчерпывающе, кратко и понятно суть основных паттернов хранения деревьев в реляционных базах данных. Надеюсь, что статья будет полезна тем, кто до сего момента не сталкивался с такими паттернами, и станет отправной точкой в их понимании.
В этой статье не будет терминов реляционной алгебры или базы данных: таких как атрибут, домен и т. д. Также не будет привязки к какой-либо СУБД, какому-либо SQL или пользовательскому коду.
Всего существует 4 общепринятых паттерна хранения деревьев:
Adjacency List;
Nested Sets;
Closure Table;
Materialized Path.
Кратко рассмотрим каждый из них.
Adjacency List
Описание
Это самый простой и интуитивный вариант хранения. Каждому элементу сопоставляется его свойство — его родительский элемент. Если родительский элемент не задан, то он считается корневым элементом.
Когда связь сопоставления элемента и родительского элемента хранится отдельно от элемента, Adjacency List можно рассматривать как частный случай Closure Table со связями 1 уровня.
Преимущества
Лёгкость реализации, а также простота вставки, удаления и перемещения элементов в дереве.
Недостатки
Можно получить только непосредственные дочерние элементы. Чтобы получить все дочерние элементы, необходимо выполнить рекурсивный запрос либо производить множественные запросы.
Примеры
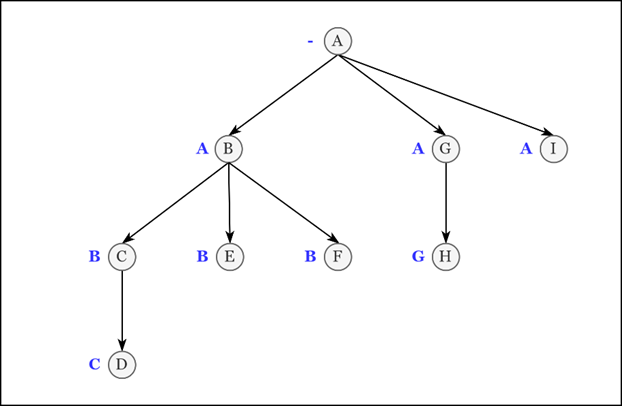
Элемент | Родительский элемент |
A | - |
B | A |
C | B |
D | C |
E | B |
F | B |
G | A |
H | G |
I | A |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
Родительский элемент равен «B»
Nested Sets
Описание
Каждому элементу сопоставляются свойства: левый и правый индекс, на основе которых будет производиться выборка дочерних элементов. Также, но необязательно, элемент может дополняться свойством уровень для указания желаемого уровня вложенности выбираемого элемента относительно корня или родительского элемента.
Запрос получения дочерних элементов строится на том факте, что для любого дочернего элемента выполняются условия:
левый индекс больше левого индекса родительского элемента;
правый индекс меньше правого индекса родительского элемента.
При создании и обновлении дерева левые и правые индексы элементов дерева, при его обходе в глубину, заполняются по определённым правилам.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.
Недостатки
При использовании целочисленных типов для левого и правого индекса и уровня необходимо пересчитывать индексы всех связанных элементов в следующих случаях:
при вставке элементов;
при удалении элементов;
при изменении родительского элемента.
Пример
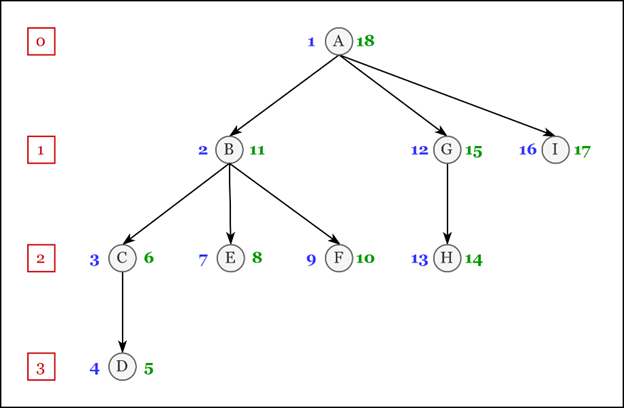
Элемент | Левый индекс | Правый индекс | Уровень |
A | 1 | 18 | 0 |
B | 2 | 11 | 1 |
C | 3 | 6 | 2 |
D | 4 | 5 | 3 |
E | 7 | 8 | 2 |
F | 9 | 10 | 2 |
G | 12 | 15 | 1 |
H | 13 | 14 | 2 |
I | 16 | 17 | 1 |
Рассмотрим элемент «B». Его значения свойств:
левый индекс = 2;
правый индекс = 11;
уровень = 1.
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
левый индекс больше 2 И правый индекс меньше 11
Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:
левый индекс больше 2 И правый индекс меньше 11 И уровень = 1
Чтобы получить дочерние элементы вместе с родительским элементом, нам необходимо ослабить условия индексов:
левый индекс больше или равен 2 И правый индекс меньше или равен 11
Closure Table
Описание
Суть этого паттерна заключается в том, что мы сопоставляем каждому элементу множество связей со всеми его дочерними элементами или сопоставляем каждому элементу множество связей со всеми его родительскими элементами. Также, но необязательно, связь может содержать свойство Уровень. Уровень задаёт расстояние между элементами в дереве.
Если в запросе получения дочерних или родительских элементов по элементу необходимо получать в результате сам элемент, то нужно добавлять связь элемента самого на себя — то есть со значением уровня связи 0.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.
Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента с помощью простого одиночного запроса.
Недостатки
При вставке и удалении элементов из дерева, а также при перемещении элементов в дереве необходимо пересчитывать все связи, в которых этот элемент участвует.
Пример
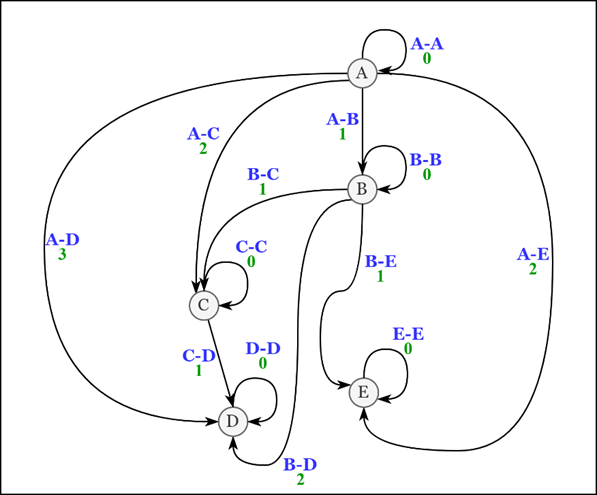
Родительский элемент | Дочерний элемент | Уровень |
A | A | 0 |
A | B | 1 |
A | C | 2 |
A | E | 2 |
A | D | 3 |
B | B | 0 |
B | C | 1 |
B | E | 1 |
B | D | 2 |
C | C | 0 |
C | D | 1 |
E | E | 0 |
D | D | 0 |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
родительский элемент равен «B»
Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:
родительский элемент равен «B» И уровень = 1
Чтобы получить дочерние элементы вместе с родительскими, нам необходимо ослабить условия индексов:
родительский элемент равен «B» И уровень = 0
Чтобы получить все его родительские элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
дочерний элемент равен «B»
Materialized Path
Описание
Каждому элементу сопоставляется свойство — его путь, который является последовательностью родительских элементов заданного элемента, отсортированных по уровням. В общем случае, чтобы формировать гибкие запросы, тип реализации свойства путь должен поддерживать сопоставление по шаблону в каком-либо виде. При денормализации пути в отдельную таблицу получается разновидность Closue Table.
Условия запросов на получение элементов заключается в применении предиката над свойством путь.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности.
Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента.
Лёгкость вставки элемента.
Лёгкость удаления элемента.
Недостатки
Сложность изменения родителя для существующего элемента. Для всех дочерних элементов необходимо пересчитать новый путь.
Операции со свойством путь обычно происходят долго.
Пример
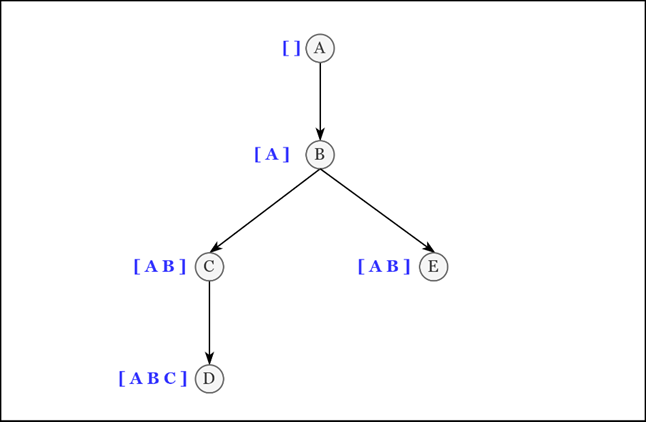
Элемент | Путь |
A |
|
B | A |
C | A B |
D | A B C |
E | A B |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
путь содержит «B»
Чтобы получить его непосредственные дочерние элементы, нужно указать позицию, в которой содержится элемент. В примере путь отсортирован так, что последняя часть пути — это непосредственный родительский элемент:
последняя часть пути равна «B»
Заключение
Мы кратко рассмотрели основные паттерны хранения деревьев в реляционной базе данных. Их основные достоинства и недоставки, а также на примерах рассмотрели основные запросы к ним. В этой статье не были рассмотрены алгоритмы построения и заполнения метаданных деревьев, то есть операции добавления, обновления и удаления элементов.