
1. Введение
В этой статье обсудим такую структуру данных, как «префиксное дерево» (оно же нагруженное дерево, бор, trie, prefix tree). Кратко рассмотрим основы и реализуем наиболее важные операции: вставку, поиск по ключу и префиксный поиск.
2. Что такое префиксное дерево?
Trie или префиксное дерево — это особый вид дерева поиска, в котором для ключей узлов обычно используются строки.
Префиксные деревья могут использоваться, например, для реализации множеств и ассоциативных массивов, но по-настоящему они проявляют себя при обходе и поиске ключей, начинающихся с определенного префикса.
По этой причине они часто используются для реализации автодополнения.
3. Структура префиксного дерева
В базовой реализации каждый узел дерева содержит один символ и указатели на дочерние узлы. Ключ узла не хранится в явном виде — он вычисляется как путь от корня до узла.
Выглядит это следующим образом:
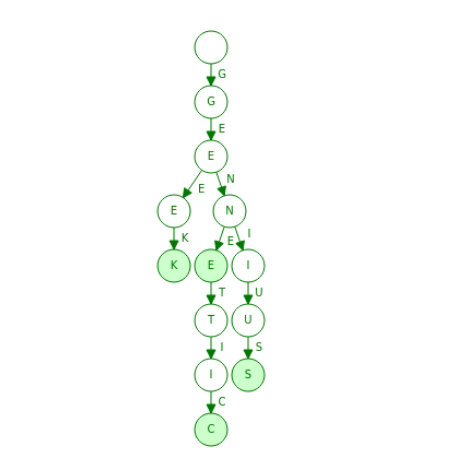
Для пометки узлов, в которых содержатся действительные ключи, используется булевый флаг. Кроме того, узлы могут содержать указатель на произвольные данные, например, при реализации ассоциативного массива.
На рисунке показано дерево с ключами: "geek", "genius", "gene" и "genetic". Закрашенные узлы представляют собой допустимые ключи. Структура дерева подразумевает, что все листовые узлы будут допустимыми ключами, но промежуточные узлы необходимо помечать отдельно.
4. Вставка
Поиск места для вставки элемента мы начинаем с корневого узла и идем по дереву вниз, создавая узлы, если они отсутствуют. После создания необходимых узлов устанавливаем флаг действительного ключа для последнего из них.
Например, слово "gene" уже содержится в дереве, и нам надо добавить "genetic":
идем по пути "gene";
создаем дополнительные узлы для "t", "i" и "c";
помечаем последний узел "c" как допустимый ключ.
Но если "genetic" уже есть в дереве, а мы вставляем "gene", то не нужно будет добавлять какой-либо новый узел в дерево.
Единственное действие, которое нужно будет выполнить — пометить конечный узел как допустимый ключ:

5. Поиск
Поиск используется для проверки наличия определенного ключа в дереве, а при реализации ассоциати��ного массива — для возврата данных, связанных с ключом.
Рассмотрим алгоритм поиска:

Поиск очень похож на вставку, но на этот раз отсутствие ключа означает отсутствие искомого значения. Если мы нашли путь, соответствующий искомому значению, то нам остается лишь проверить действительный ли это ключ.
Обратите внимание, что как в алгоритме вставки, так и в алгоритме поиска нам не нужно было обходить дерево, используя, например, поиск в глубину или в ширину. Это не требовалось, потому что путь, по которому мы должны следовать, непосредственно содержится во входных данных.
6. Поиск по префиксу
Мы рассмотрели основные операции над префиксным деревом. Теперь пришло время поговорить о том, где префиксное дерево наиболее эффективно — поиск слов с заданным префиксом.
Для этого:
найдем путь для префикса "P", начиная с корня;
начиная с последнего узла пути "L" вычислим всех потомков "L", которые являются допустимыми ключами;
вернем найденные узлы.
Вот как это выглядит на практике:

7. Выводы
В этой статье мы познакомились с префиксным деревом и узнали, как реализовать основные операции: вставка, поиск, а также поиск по префиксу.
Дерево отрезков — это структура данных, которая позволяет алгоритмически просто и логарифмически быстро находить сумму элементов массива на заданном отрезке. Приглашаем на открытый бесплатный урок, на котором мы рассмотрим идею дерева отрезков, узнаем, как его строить, обновлять и быстро O(log n) вычислять сумму чисел любого отрезка данного массива. Алгоритм очень простой и экономный: нужно O(n) памяти. Регистрация для всех желающих доступна по ссылке.
