high_fly 26 июл 2022 в 23:35

LASSO и Ridge Регрессия. Что же значит та картинка

8 мин

26K

Пыталась я вникнуть в устройство регрессии LASSO и Ridge… И сделала объективный вывод, что верхнеуровнево про них много где хорошо и подробно написано. Человеку непосвящённому легко найти понятные объяснения, просто погуглив. Но я-то человек посвящённый! Я хочу понять! Но вот беда — в русскоязычных блогах я нигде не смогла найти толкового прояснения некоторых метаматематических моментов работы лассо и ридж регрессии. Пришлось доходить до понимания самой с опорой на пару англоязычных источников, и я решила изложить некоторую математику, лежащую в основе лассо и ридж в этой статье.

И снова про регрессию (полиномиальную)

Начнём с основных определений. Представим, что у нас есть наблюдения, которые характеризует один признак. Например, мы хотим предсказать количество предстоящих лет жизни человеку по его индексу массы тела — такое вот у нас исследование. У нас есть набор данных “с ответами” — то есть табличка соответствия “ИМТ в 30 лет → n оставшихся лет” собранная с населения какой-нибудь скандинавской страны.

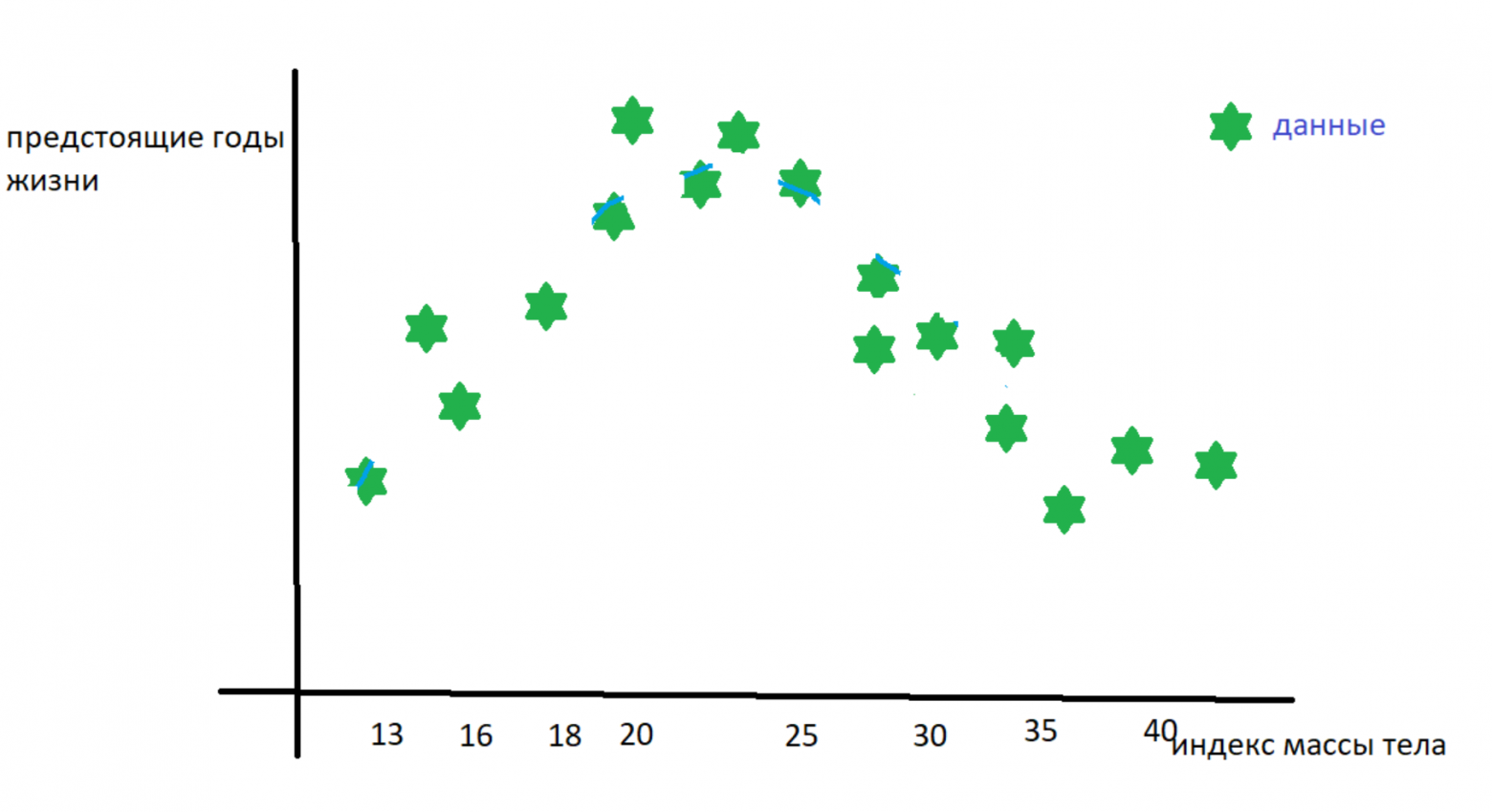
Дальше всякими правдами и не-правдами догадываемся, что зависимость годов жизни от ИМТ описывается полиномом степени 2, а значит надо искать три коэффициента — при , и при (он же сдвиг кривой по оси ординат).

Чтоб найти коэффициенты, возьмём наш набор наблюдений-иксов и “раскроем его” — вместо одного икса сделаем икс в нулевой, икс в первой (он же просто икс) и икс в квадрате, — чтоб найти уместные коэффициенты перед каждым компонентом уравнения полиномиальной регрессии.

Решим матричное уравнение. В матрице у нас каждый ряд представляет собой одно наблюдение, в нашем случае - одного человечка. Вектор w — искомый вектор коэффициентов регрессии. Вектор игрек — вектор количества лет — одно число для каждого человечка. Хорошо про решение таких уравнений для поиска коэффициентов регрессии написано тут.

$\begin{equation*} \left( \begin{array}{ccc} 1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2\\ \vdots & \vdots & \vdots\\ 1 & x_n & x_n^2 \end{array} \right) \end{equation*} \cdot \left( \begin{array}{c} w_0 \\ w_1 \\ w_2 \end{array} \right) = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right)$

Решаем и получаем что-то типа — искомый полином степени 2.

предположения о зависимости ИМП и лет жизни тоже взяты с потолка

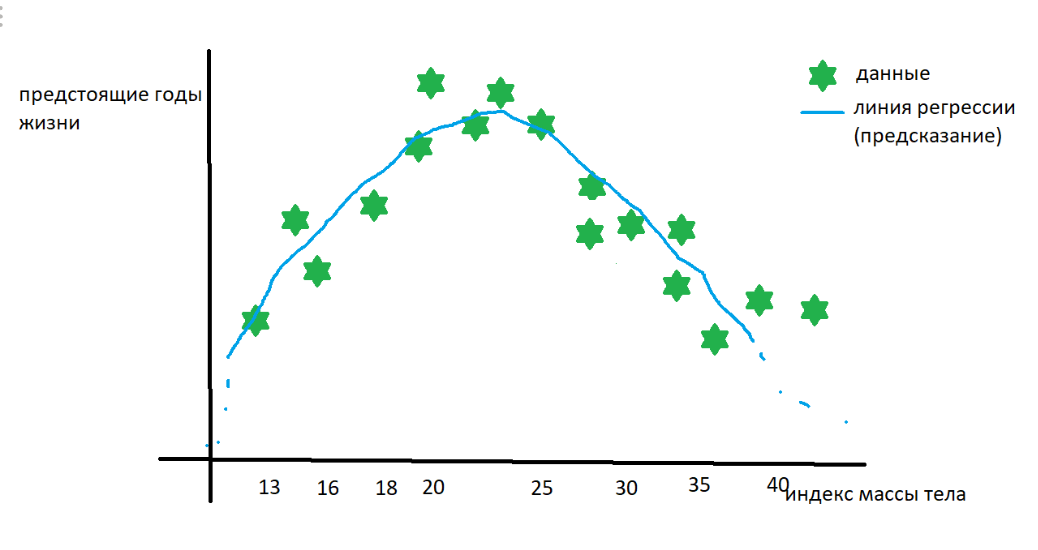
Bam! Мы построили линию регрессии и теперь по ИМТ можем предсказывать дату смерти!

И снова про проклятие размерности

На самом деле и в жизни, и в науке исследователи далеко не всегда знают, какие признаки влияют на целевую переменную. Влияет ли на доходность бизнеса средняя продолжительность рабочего дня CEO компании? А широта и долгота главного офиса компании? Влияет ли на дату смерти человека аномалии в гене OCA2 (один из генов, кодирующих цвет радужки)?

Часто исследователи стараются зафиксировать как можно больше признаков — порода домашнего животного, ИМТ, уровень глюкозы, рост — просто на всякий случай. Но если мы будем учитывать все собранные признаки, то существует риск большой дисперсии модели на новых данных. Конечно, если у нас для одного человека собрано 100 фич, среди которых ИМТ, цвет глаз, порода собаки, количество морганий в минуту, то модели будет сложно выделить действительно значимые тренды и при изменении одного, даже самого незначительно признака (например, количество морганий изменили на +2) предсказание — оставшиеся года жизни — изменится радикально. И вот уже человеку жить не 50 лет, а 30. А ещё может быть такой случай — признаки, которые мы собрали, сильно скоррелированы. Например, вес человека утром и вес человека перед сном. Скоррелированные признаки сильно мешают нам в решении матричного уравнения, так как становится трудно построить обратную матрицы. Подробнее про такие плохо обусловленные задачи написано тут.

Представим, что мы собрали чуть больше данных о наших скандинавских ребятах. Теперь у нас есть не только их ИМТ, но ещё количество морганий в час. Теперь признаковое пространство стало двумерным. Координата точки по икс1 и икс2 — в нижней полуплоскости — даёт нам представление о том, какой у человека ИМТ и сколько раз в час он в среднем моргает. Красная парящая точка в воздухе — есть предсказание оставшиеся лет.

Попробуем развернуть это трёхмерное пространство — разбить его на два двумерных и посмотреть на зависимость целевой переменной от каждого признака.

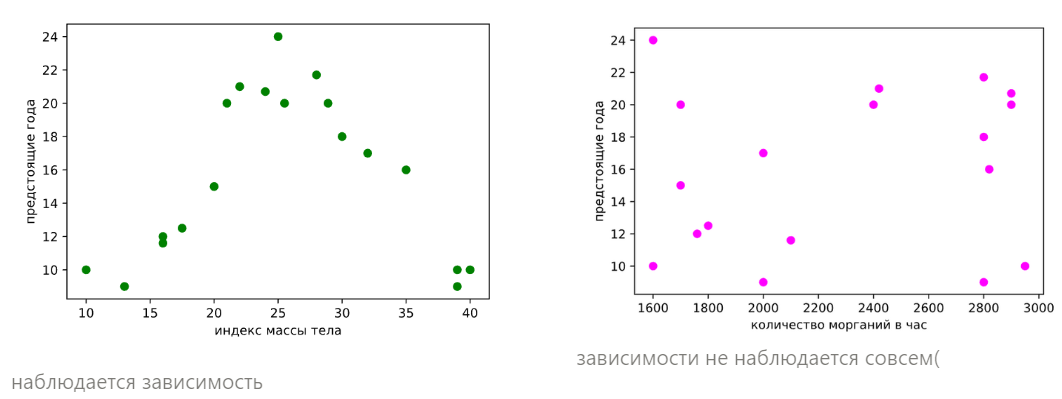
Итак, теперь нам очевидно, что зависимости между количество морганий в час и годами нет. Даже на глаз, не говоря уже о логике. Но что, если у нас миллион таких признаков и 10 миллионов наблюдений? Не смотреть же миллион графиков. Да и зависимости могут быть хитрее. В общем, хотелось бы какое-нибудь изящное математическое решение проблемы, чтоб математика сама признаки, которые не вносят вклад в предсказание, убирала. А ещё чтоб избавлялась от скоррелированных признаков. К примеру, если б мы решили о наших скандинавах собирать вес в килограммах и индекс массы тела, хотелось бы, чтобы модель нам деликатно один из этих высоко-скорелированных признаков убрала. Где же такая волшебная машина?

И снова про регуляризацию

В общем, стало быть, в задаче со ста фичами, когда мы предполагаем, что значимыми являются ну максимум 20, нам надо как-то эти 20 определить. Тут на помощь приходит регуляризация.

🅾️ Регуляризация — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение.
(с) Вики

В нашей задаче мы хотим выкинуть признак с морганием.

Мы знаем, что для того, чтоб построить модель машинного обучения, мы используем функцию потерь. Грубо говоря, чем меньше функция потерь, тем лучше. Регрессии лассо и ридж от обычной регрессии отличаются только наличием штрафа в функции потерь. Вот, кстати, и они, функции потерь лассо и ридж, слева направо (сверху вниз)

$J_{LASSO} = \sum_i (y_i - \hat{y})^2 + \lambda ||w||$ $J_{RIDGE} = \sum_i (y_i - \hat{y})^2 + \lambda w^2$

Лямбда - гиперпараметр, который мы можем настраивать вручную. Чем больше лямбда, тем сильнее модель штрафуется за величину коэффициентов и их количество. Если занулить лямбду, мы получим самую обычную функцию потерь методом наименьших квадратов, соответственно — самую обычную регрессию. То если в лассо и ридж модель пытается найти баланс между хорошим предсказанием, которое подходит под тренировочные данные, и не слишком большой сложностью модели, когда мы используем не все фичи и не делаем коэффициенты огромными (10 000, 100 000 и т.д.). Понятно, что чем длиннее вектор коэффициентов (то есть чем больше в нём мы рассматриваем фич) и чем больше эти коэффициенты по модулю, тем сильнее будет штрафоваться модель.

Существенно отличие регрессии лассо от ридж в том, что лассо зануляет коэффициенты. То есть буквально перед какими-то фичами она ставит 0 и в модели они не рассматриваются. Ридж же может коэффициент сильно уменьшить, но не занулить. Почему так?

Объяснения LASSO и Ридж. Та Самая Картинка

Почему так? Нам отвечает супер-известная картинка, которая в разных вариантах присутствует, наверное, в каждой статье о лассо и ридж. Дальше в статье я буду отсылаться к ней как к Той Самой Картинке. Та Самая Картинка должна объяснять, почему лассо зануляет коэффициенты, а ридж нет. Только вот в русскоязычных статьях я Толкового Толкования этой картинки для себя не нашла. Теперь, надеюсь, кому-то проще будет понять.

Итак, на Той Самой Картинке мы пытаемся оптимизировать регрессию с двумя фичами - $\beta_1$ и $\beta_2$ . Это могут быть коэффициенты обычной линейной регрессии $y=\beta_2\cdot x + \beta_1$ . Это могут быть два разных признака, например, рост отца и рост матери, когда мы пытаемся предсказать рост ребёнка. По сути мы ищем такую точку на плоскости с координатами $\beta_{1_{идеальное}}$ и $\beta_{2_{идеальное}}$ , чтоб она соответствовала минимуму функции ошибок.

С осями разобрались. А что за красные овалы? Красные овалы есть квадратичная функция потерь обычной линейной регрессии без всякого штрафа. Причём это вид на функцию сверху. Вспомним, как вообще выглядит функция ошибок SSE (sum of squered errors) с двумя параметрами. Меняться могут два параметра, следовательно функция ошибок - трёхмерная, и принимает вид этакой чаши, а по-научному — параболоида. Минимум квадратичной функции ошибок — на дне чаши.

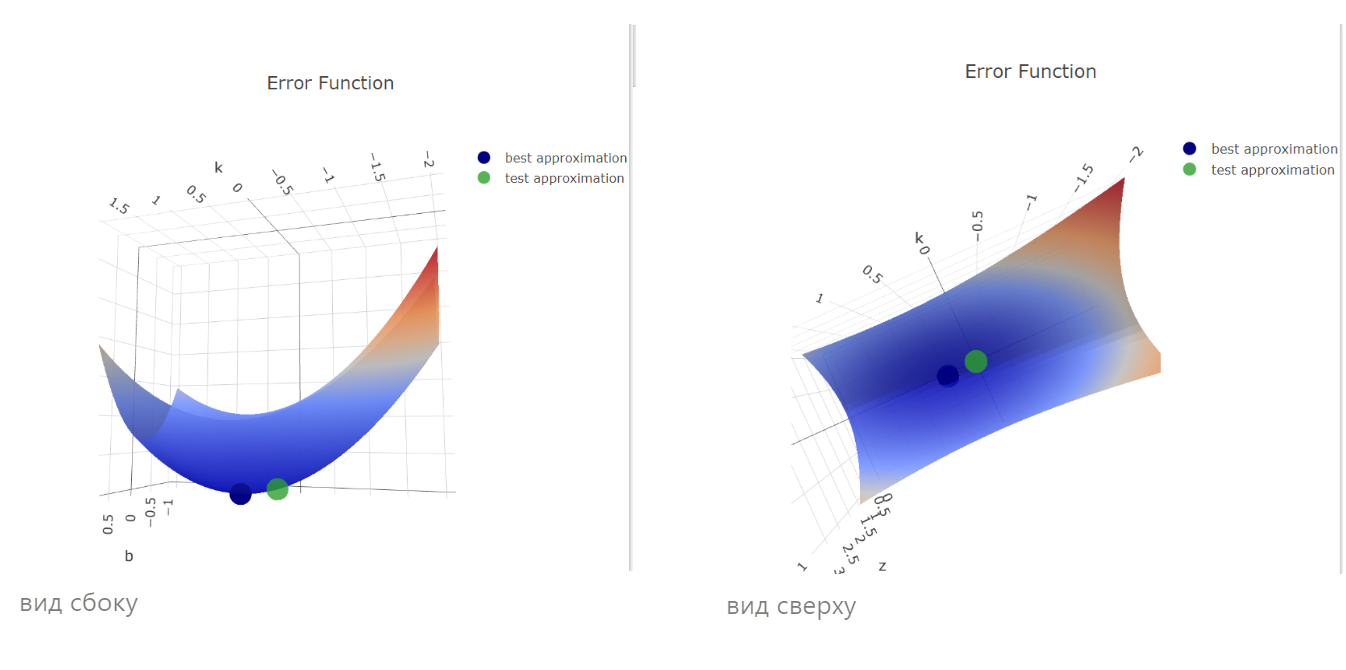
ссылка на интерактивную визуализацию

Вернёмся к Той Самой Картинке. Красные овалы — это вид на функцию потерь сверху. А точка $\hat{\beta}$ — это точка на дне чаши, минимум квадратичной ошибки. И если б у нас была обычная регрессия, не лассо и не ридж, то мы бы взяли коэффициенты $\beta_1$ и $\beta_2$ , соответствующие точке $\hat{\beta}$ и всё, готова наша регрессия. Но у нас есть штраф! И этот штраф не даёт нам взять $\hat{\beta}$ , а заставляет искать другое значение.

Дело в том, что штраф, очевидно, накладывает некоторое ограничение на наши коэффициенты. На Той Самой Картинке это ограничение изображено как голубой квадрат и зелёный круг. В случае с лассо мы говорим, что сумма модулей наших коэффициентов не должна быть больше некоторого t. t - это некоторое число, которое зависит от величины лямбда (чем больше лямбда, тем меньше t) и от диапазона наших наблюдений, для разных данных t будет разным. Факт в том, что если сумма модулей коэффициентов становится чуть больше t, то функция потерь лассо $J_{LASSO} = \sum_i (y_i - \hat{y})^2 + \lambda ||w|$ становится настолько большой, что в этой точке никак не может быть её минимум. Неравенство $|\beta_1|+|\beta_2|\leq t$ выполняется только внутри квадрата и на его границах, соответственно, везде вне квадрата штраф будет слишком большой, чтоб там был искомый нами минимум.

Можно заметить, что оптимальная с точки зрения квадратичной функции потерь точка $\hat{\beta}$ находится вне голубого квадрата. Однако $\beta_1$ и $\beta_2$ в ней слишком большие, чтобы удовлетворить ограничения штрафа. Что ж, придётся подниматься вверх по чаше квадратичной функции потерь, пока мы не найдём такие $\beta_1$ и $\beta_2$ , что они удовлетворят ограничению штрафа.

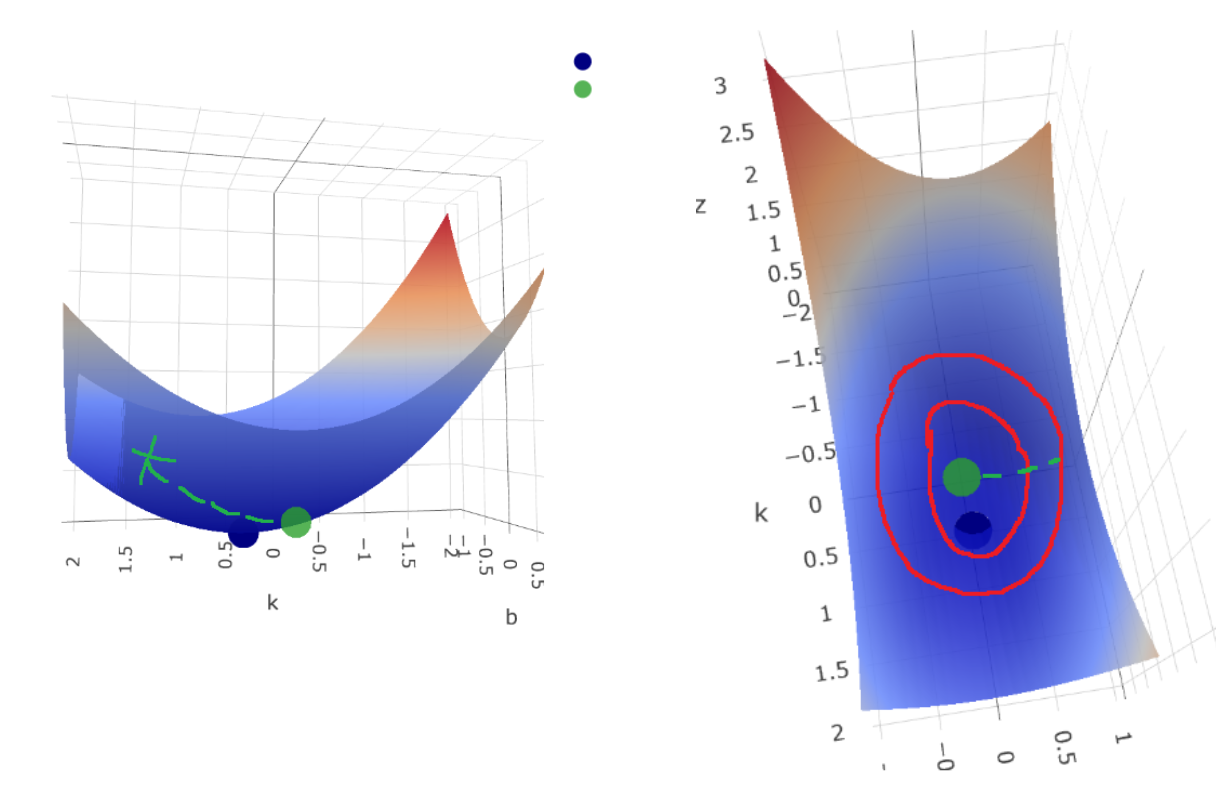
Мы начинаем ползти вверх. Зелёным пунктиром обозначен наш путь. Зелёный крестик - оптимальные $\beta_1$ и $\beta_2$ с точки зрения функции потерь лассо. Второй рисунок — вид сверху. На Той Самой Картинке множественные красные овалы как раз обозначают наш путь вверх по чаше, вверх по квадратичной функции потерь. Заметьте, что зелёный крестик вовсе не соответствует минимуму квадратичной функции ошибок, минимум у нас в синем кружочке. Зато зелёный крестик позволяет $\beta_1$ и $\beta_2$ уменьшится настолько, что штраф милостиво пропускает такие значения, а значит мы достигаем минимума по функции потерь лассо $J_{LASSO} = \sum_i (y_i - \hat{y})^2 + \lambda ||w||$ .

На Той Самой Картинке оптимум находится в точке пересечения красного круга и грани квадрата. Мы нашли то самое равновесие — квадратичная ошибка не так велика, не так велик штраф. Мы могли бы сдвинуться ещё внутрь голубого квадрата — штраф бы стал ещё меньше, так как меньше стали бы $\beta_1$ и $\beta_2$ . Но тогда скакнула бы вверх функция квадратичной ошибки, ведь мы бы забрались ещё выше по стенкам её чаши. Мы могли бы не доходить до голубого квадрата вообще и попытаться уменьшить квадратичную функцию ошибки, но тогда штраф за большие значения $\beta_1$ и $\beta_2$ был бы слишком велик.

И вот так, регрессия лассо позволяет нам достигать оптимума — не слишком большая ошибка, не слишком сложная модель. Таким образом лассо уменьшает дисперсию модели на тестовых данных, позволяет нам выкинуть бесполезный признак “количество морганий в час” из нашего датасета, который бы только вносил шум в наше предсказание.

наш оптимум — помесь не-слишком-большой-ошибки и не-слишком-большого-штрафа

Заметьте, что на Той Самой Картинке в случае лассо оптимум достигается там, где $\beta_1$ равно нулю. Почему именно там? Потому что мы, путешествуя по стенке чаши и уменьшая сумму модулей коэффициентов, наткнёмся на уголок квадрата неравенства $|\beta_1|+|\beta_2|\leq t$ раньше, чем на что-то другое. Он просто как бы повёрнут нам навстречу. А так как уголок неравенства всегда будет лежать на оси $\beta_1=0$ , мы всегда будем занулять один из коэффициентов.

UPD

Как справедливо указали в комментариях - нет, не всегда. В Лассо может случится ситуация, когда функция ошибок столкнётся с квадратом на грани квадрата, а не на его уголке. А Ридж в свою очередь тоже может занулить какой-то из коэффициентов. Другое дело, что из-за того, что штраф лассо - квадратный (или кубический, или гиперкубический), то есть у него много острых углов и рёбер, у функции ошибок вероятность наткнуться на ребро или угол больше, следовательно и вероятность занулить один или больше коэффициентов больше.

Вот, например, ситуация, когда регрессия Лассо не занулит ни один из коэффицентов, а ридж - возьмёт и занулит 😱. За рисунок спасибо @vbogach

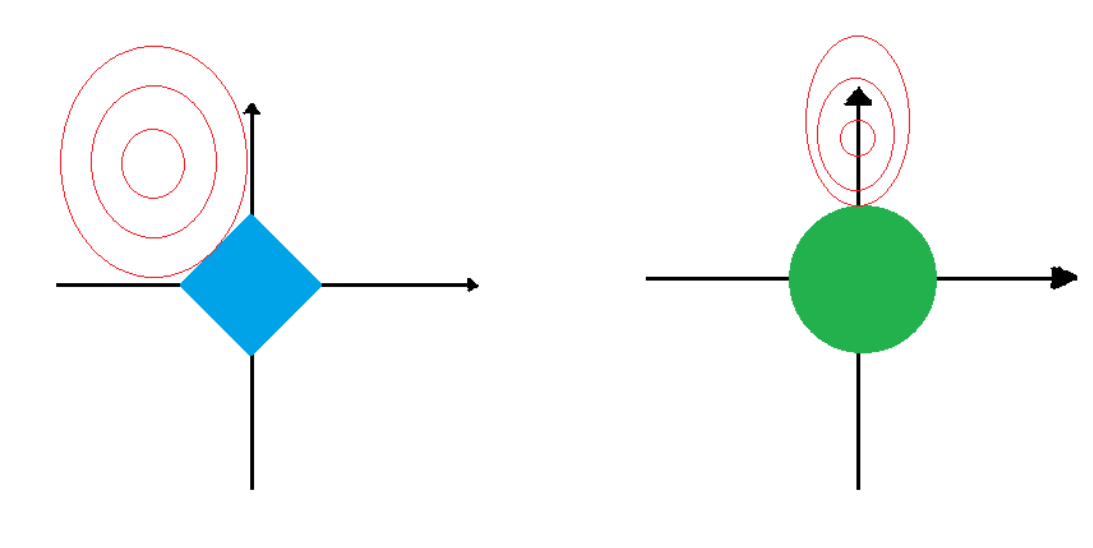
На Той Самой Картинке слева, там, где изображена регрессия ридж, ситуация такая же за одним исключением — оптимум там достигается не там, где $\beta_1=0$ , а там, где $\beta_1$ почти ноль. А с чем же это связано? Дело в том, что в случае с ридж-регрессией штраф выглядит иначе: $J_{Ridge} = \sum_i (y_i - \hat{y})^2 + \lambda w^2$ . Здесь в штрафе коэффициенты возводим в квадрат. Значит, и ограничение, накладываемое штрафом выглядит иначе: $\beta_1^2+\beta_2^2\leq c$ . Это уравнение окружности. Внутри окружности и на границах штраф достаточно мал, снаружи — слишком велик. Оптимальные коэффициенты снова находятся там, где овал функции потерь в первый раз встречается со штрафом. Только теперь это будет не на оси $\beta_1=0$ , потому что в случае с кругом, гладкий славный бочок круга всегда встретится с овалом функции потерь раньше, чем она встретится с осью $\beta_1=0$ . Именно поэтому ридж и не попадает в ноль. Тем не менее, видно, что на Той Самой Картинке коэффициент $\beta_1$ находится достаточно близко к нулю.