honyaki 19 авг 2022 в 23:47

О новом простом методе снижения высокой размерности данных

8 мин

8.1K

Блог компании SkillfactoryPython*Математика*R*Matlab*

Перевод

О новом методе решения проблемы оценки ковариационной матрицы в данных высокой размерности [научная работа опубликована в 2012 году] рассказываем к старту нашего флагманского курса по Data Science. Подробности — под катом:

Оптимальная оценка ковариационной матрицы в больших размерностях

Приложения в области статистики, машинного обучения и даже в таких областях, как финансы и биология, часто нуждаются в точной оценке ковариационной матрицы. Однако в настоящее время многие из этих приложений используют данные высокой размерности, и поэтому обычная (выборочная) ковариационная оценка просто не подходит. Таким образом, множество работ за последние два десятилетия пытались решить именно эту проблему. Чрезвычайно мощный метод, появившийся в результате этих исследований, — «нелинейное снижение размерности» [1]. Я сосредоточусь на новейшей версии этого подхода, квадратичном обратном линейном снижении размерности (QIS) от [2]. Этот подход делает нелинейное снижение размерности простым в реализации и быстрым для вычисления.

А на наших курсах вы научитесь применять математику в решении конкретных проблем бизнеса:

Профессия Data Scientist (24 месяца)

Профессия Data Analyst (18 месяцев)

Давайте начнём с основ (если вы уже имели дело с ковариационными матрицами, то можете смело пропустить этот раздел).

Основы

Ковариационная матрица содержит дисперсии и ковариации двух или более случайных величин. То есть, если мы посмотрим на случайные величины $inline$ , $inline$ и $inline$ , то ковариационная матрица будет иметь вид:

Поскольку ковариация между $inline$ и $inline$ и $inline$ и $inline$ одинакова, матрица обязательно будет симметричной. Более того, из линейной алгебры мы знаем, что эта матрица имеет так называемое разложение на собственные значения, т. е.

Важной частью здесь является лямбда-матрица, которая представляет собой диагональную матрицу, содержащую собственные значения ковариационной матрицы

Таким образом, мы можем диагонализовать ковариационную матрицу, а её диагональные элементы будут содержать важную информацию. Например, они сразу сообщают нам ранг ковариационной матрицы: то есть, просто количество ненулевых собственных значений. Если матрица имеет полный ранг, т.е. все её собственные значения больше нуля, это означает, что случайные величины полностью разбросаны в $inline$ -мерном пространстве. Это также очень полезно, потому что

В частности, мы видим, что ковариационная матрица обратима тогда и только тогда, когда все её собственные значения отличны от нуля или если ранг матрицы равен $inline$ .

Каждая симметричная матрица может быть разложена на произведение ортогональных матриц и (вещественной) диагональной матрицы. Значения диагональной матрицы раскрывают важные свойства и могут использоваться для лёгкого вычисления обратной матрицы, если она существует.

Проблема

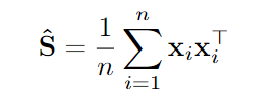
Предположим, что теперь у нас есть выборка из $inline$ независимых одинаково распределённых случайных векторов в $inline$ -измерениях с ожидаемым значением, равным нулю (для простоты). Ковариационная матрица $inline$ может оцениваться с помощью обычной выборочной ковариационной матрицы (далее — ВКМ):

Это оказывается как раз оценкой максимального правдоподобия, если распределение ваших данных соответствует распределению Гаусса. Такая оценка обладает всевозможными благоприятными свойствами и, в частности, известно, что она сходится к истине, когда $inline$ стремится к бесконечности, а $inline$ остаётся постоянным (или медленно растёт относительно $inline$ так, что $inline$ стремится к нулю).

Однако обратите внимание, что в приведённой выше матрице у нас есть элементы $inline$ для оценки. Здесь $inline$ — это количество способов выбрать два элемента из $inline$ , которое мы делим на 2, потому что матрица симметрична. В выборке $inline$ это становится проблемой, если $inline$ не намного больше, чем $inline$ ! Это легче всего увидеть, когда $inline$ оказывается больше $inline$ . В этом случае можно показать, что ВКМ матрица $inline$ имеет ранг не более чем $inline$ . В частности, даже если истинная ковариационная матрица обратима (имеет все собственные значения больше нуля), ВКМ будет иметь $inline$ нулевых собственных значений и, таким образом, никогда не будет обратимой. Поэтому, если вам нужна оценка обратной ковариационной матрицы, как в линейном дискриминантном анализе или при вычислении значения гауссовой плотности, это может оказаться проблемой.

Это может показаться крайностью, но даже если у вас есть, скажем, $inline$ , ошибка оценки ВКМ может быть существенной. Давайте теперь посмотрим на удачный способ решения этой проблемы.

Решение

Тут я буду радикален. Конечно, у этой проблемы есть множество решений, и в зависимости от ситуации некоторые из них работают лучше других. Даже простое изменение того, как вы измеряете успех, может изменить порядок методов.

Возможно, простая идея, которая привела к множеству исследований и появлению новых приложений, состоит в том, чтобы просто взять линейную комбинацию ВКМ и единичной матрицы:

Интенсивность снижения размерности $inline$ может быть выбрана различными способами, но чаще всего она автоматически выбирается по данным из теоретических соображений. Если рассматривать разложение на собственные значения тождества и ВКМ, то мы уже видим нечто своеобразное:

Получается, у нас просто есть новые собственные значения, которые являются выпуклой комбинацией ВКМ и $inline$ . Таким образом, если $inline$ -тое собственное значение было равно 2, то регуляризованное значение теперь равно $inline$ . В частности, поскольку наименьшее собственное значение ВКМ равно 0, наименьшее регуляризованное собственное значение теперь равно $inline$ . Итак, пока $inline$ , регуляризованная матрица всегда будет обратимой! Формула также может быть знакома по L2-регуляризованной регрессии:

Принцип, согласно которому собственные векторы остаются неизменными, а собственные значения адаптируются, является важным в этих методах уменьшения размерности. Это имеет смысл, потому что, как правило, бесполезно правильно оценивать все параметры, когда $inline$ близко или превышает $inline$ . Но собственные значения $inline$ — это совсем другая история, и они могут быть достижимы. Это основная идея нелинейного уменьшения размерности, из-за этой идеи оно на шаг впереди.

Оценка собственных векторов в большой размерности бесполезна. Таким образом, важным принципом является адаптация собственных значений и просто сохранение собственных векторов неизменными.

В приведённом выше линейном уменьшении размерности, если выбрать $inline$ «правильно», то можно фактически достичь оптимальной производительности в асимптотическом пределе, когда и $inline$ , и $inline$ идут вместе до бесконечности. Это было установлено в статье 2004 г. [3] и показывает оптимальную оценку собственного значения, если класс оценок является линейным, как в примере выше. То есть класс линейных оценок снижения размерности — это просто все оценки вида (1) при изменении $inline$ .

Нелинейное уменьшение размерности даёт асимптотическую оценку в гораздо более крупном классе, который не обязательно должен быть просто линейной функцией ВКМ. В частности, решает проблему

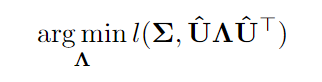
где $inline$ — некоторая функция потерь. Мы ищем выбор (уменьшенных) собственных значений, который максимально приближает результирующую матрицу к истинной ковариационной матрице, если нам разрешено использовать только собственные векторы ВКМ! Как мы видели ранее, линейное уменьшение размерности является частным случаем этого, потому что мы также меняем только собственные значения. Однако теперь способ, которым мы определяем лямбду, не ограничивается линейностью, что обеспечивает гораздо большую гибкость!

Интересно, что (недостижимое) оптимальное решение вышеизложенного вполне интуитивно понятно:

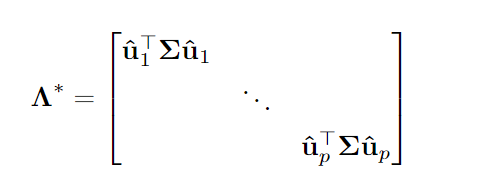
где $inline$ — это просто примеры собственных векторов из предыдущего:

То есть лучшим решением для собственных значений в этом контексте являются не истинные значения, а то значение, которое мы получаем, когда применяем собственные векторы ВКМ к истинной ковариационной матрице.

Лучшее, что мы можем сделать для диапазона функций потерь, — это оценить значения, которые получаются, когда выборки собственных векторов применяются к истинной ковариационной матрице.

Оказывается, метод нелинейного снижения размерности способен последовательно оценивать эти оптимальные элементы, когда $inline$ и $inline$ вместе стремятся к бесконечности! Давайте теперь посмотрим на пример.

Пример кода

Итак, нелинейное снижение размерности красиво выглядит в теории, но применимо ли оно на практике? Вот тут-то и появляются две совсем недавние статьи, благодаря которым нелинейное снижение размерности превратилось из причудливой идеи, требующей больших вычислений, в реально используемый инструмент. В частности, метод QIS (квадратичное обратное линейное снижение размерности, [2]) можно рассчитать в несколько строк кода! Но вам даже этого делать не нужно, так как весь необходимый код [Python, R, MatLab] доступен здесь.

Давайте рассмотрим приложение в R, использующее функцию qis. В этом примере мы берём сложную истинную ковариационную матрицу, которая имеет

Так, в частности, дисперсия равна 1, и чем дальше друг от друга индексы $inline$ и $inline$ , тем меньше ковариация между ними. Таким образом, элементы ковариационной матрицы экспоненциально приближаются к нулю по мере нашего движения вправо, но многие из них всё равно будут больше нуля. Давайте используем $inline$ и $inline$ в этом примере, так что $inline$ :

library(mvtnorm)
source("qis.R")

set.seed(1)

n<-800
p<-1000
rho<-0.7

# Generate the covariance matrix
Sig<-sapply(1:p, function(i) {sapply(1:p, function(j) rho^{abs(i-j)} ) }  )
# Take the eigendecomposition of the true covariance matrix
spectral<-eigen(Sig)
# Simulate data
X<-rmvnorm(n = n, sigma = Sig)

# Take the eigendecomposition of the scm
samplespectral<-eigen(cov(X))

# Use QIS and take the eigendecomposition
Cov_qis <- qis(X)
qisspectral<-eigen(Cov_qis)

# Rename
qisspectral$U<-qisspectral$vectors
qisspectral$Lambda<-qisspectral$values

# Want u_j'*Sig*u_j for all j=1,...,p
whatwewant<-diag( t(qisspectral$U)%*%Sig%*%qisspectral$U  )

#check on first value whether its really calculated correctly
(whatwewant[1]-t(qisspectral$U[,1,drop=F])%*%Sig%*%qisspectral$U[,1,drop=F])

Код моделирует данные из 1000-мерной нормали и вычисляет выборочную ковариационную матрицу с её собственными значениями. Обратите внимание, что это работает без проблем, несмотря на то, что $inline$ . Это одна из опасностей ВКМ, она работает даже тогда, когда это может быть неуместно. Затем вычисляется матрица QIS вместе с собственными значениями и собственными векторами (которые совпадают с собственными векторами ВКМ). Наконец, мы вычисляем теоретическое оптимальное решение, рассмотренное выше.

Давайте построим график:

plot(sort(samplespectral$values, decreasing=T), type="l", cex=0.8, lwd=1.5, lty=1)
lines(sort(spectral$values, decreasing=T), type="l", col="darkblue", cex=0.8, lwd=1.5, lty=2)
lines(sort(whatwewant, decreasing=T), type="l", col="darkred", cex=0.8, lwd=1.5,, lty=3)
lines(sort(qisspectral$Lambda, decreasing=T), type="l", col="darkgreen", cex=0.8, lwd=1.5, lty=4)

legend(500, 20, legend=c("Sample Eigenvalues", "True Eigenvalues", "Attainable Truth", "QIS"),
       col=c("black", "darkblue", "darkred", "darkgreen"), lty=1:4, cex=0.8)

Что даёт

Чем интересен этот график? Во-первых, мы видим, что выборочные собственные значения сильно отличаются — они оказываются выше самых больших собственных значений и ниже самых маленьких. В частности, последние 1000 – 800 = 200 собственных значений равны нулю. Эта «сверхдисперсия» хорошо известна в больших размерностях: малые собственные значения оцениваются как слишком маленькие, а большие — как слишком большие. С другой стороны, мы видим, что нелинейно уменьшенные собственные значения (выделены зелёным) довольно близки к истинным значениям, показанным синим. Что ещё более важно, они очень близки к красной линии, которая является достижимой истиной выше, то есть $inline$ !

Действительно, тогда оценка общей матрицы лучше более чем на 30%:

((norm(cov(X)-Sig,type="F")-norm(Cov_qis-Sig, type="F"))/norm(Cov_qis-Sig, type="F"))
[1] 0.3088145

Эта разница может быть намного больше в зависимости от формы истинной базовой ковариационной матрицы. Важно отметить, что QIS работает примерно так же, как и обычная оценка ковариационной матрицы, когда $inline$ очень мало по сравнению с $inline$ , и становится (намного) лучше, как только $inline$ растёт относительно $inline$ . Таким образом, если $inline$ достаточно велико, то есть $inline$ , может быть даже выгодно всегда использовать QIS напрямую!

Заключение

В этой статье даётся представление о методе нелинейного снижения размерности выборочной ковариационной матрицы. После более концептуального/математического введения, небольшой пример кода иллюстрирует метод в R. Код для метода также доступен в Matlab и Python.

Есть много реальных приложений, где широко используется этот метод, в частности, в области финансов. Знаете ли вы другие приложения, где это может быть полезно, из вашего собственного рабочего опыта? Я всегда рад услышать об интересных вариантах использования и наборах данных.

Литература

[1] Ledoit, O. and Wolf, M. (2012). Nonlinear Shrinkage Estimation of Large-Dimensional Covariance Matrices. The Annals of Statistics, 40(2):1024–1060.

[2] Ledoit, O. and Wolf, M. (2022). Quadratic Shrinkage for Large Covariance Matrices. Bernoulli, 28(3):1519–1547.

[3] Ledoit, O and Wolf, M (2004). A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices. Journal of Multivariate Analysis, 88(2):365–411.

А мы поможем прокачать ваши навыки или с самого начала освоить профессию, востребованную в любое время:

Профессия Data Scientist (24 месяца)

Профессия Data Analyst (18 месяцев)

Профессия Fullstack-разработчик на Python (15 месяцев)

Теги:

Хабы: