Книга «Математические алгоритмы для программистов. 3D-графика, машинное обучение и моделирование на Python»

Приветствуем вас, дорогие Хаброжители!

Неважно, чем вы занимаетесь — большими данными, машинным обучением, компьютерной графикой или криптографией — без математики вам не обойтись! Везде сейчас требуются базовые знания и понимание алгоритмов.

Практические примеры позволят легко разобраться с самыми необходимыми математическими понятиями. 300 упражнений и мини-проектов откроют вам новые возможности в освоении интересных и популярных IT-профессий. Вы познакомитесь с базовыми библиотеками Python, используемыми при разработке реальных приложений, и вспомните давно забытые основы линейной алгебры и матана.

Скорость изменения

Рассмотрим простой пример из моей практики анализа данных о добыче нефти.. Представьте насос, поднимающий сырую нефть из скважины и подающий ее по трубе в резервуар. Труба оборудована датчиком-расходомером, непрерывно измеряющим скорость потока жидкости, а резервуар — датчиком-уровнемером, определяющим уровень жидкости в резервуаре и сообщающим объем нефти, находящейся внутри (рис. 8.1).


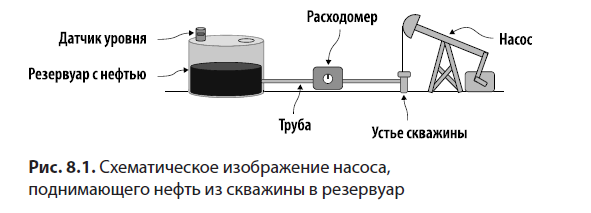
Показания датчика уровня сообщают объем нефти в резервуаре в виде функции от времени, а показания расходомера сообщают объем нефти, поступающей в резервуар в единицах объема в час и тоже в виде функции от времени. В этом примере объем является суммарным значением, а расход — скоростью его изменения.

В этой главе мы будем решать две основные задачи. Во-первых, начав с известных суммарных объемов в разные моменты времени, вычислим расход как функцию от времени, используя производную. Во-вторых, решим противоположную задачу: начав с расхода как функции от времени, вычислим суммарный объем нефти в резервуаре в заданный момент времени с помощью интеграла. Этот процесс показан на рис. 8.2.


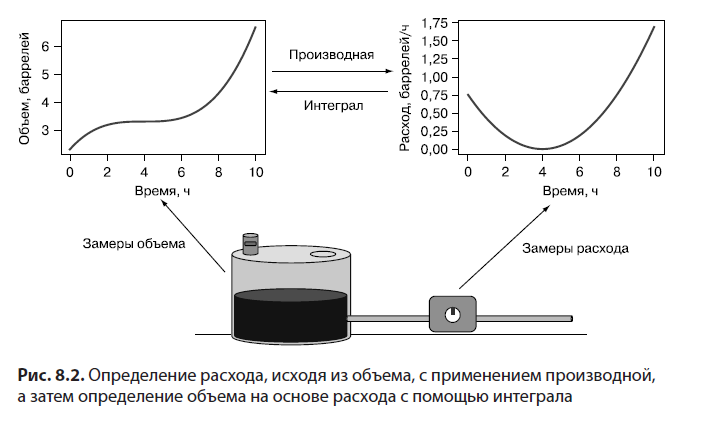
Мы напишем функцию get_flow_rate(volume_function), которая принимает функцию объема и возвращает новую функцию, вычисляющую расход в данный момент времени. Затем напишем вторую функцию, get_volume(flow_rate_function), которая принимает функцию расхода и возвращает функцию, дающую объем в данный момент времени. Попутно я добавлю несколько небольших примеров для разминки, чтобы направить ваши размышления о скорости изменений в правильное русло.

Несмотря на то что основные идеи матанализа не особенно сложны, он считается трудным предметом, потому что требует большого объема утомительных алгебраических вычислений. Поэтому в данной главе я сосредоточусь на представлении новых тем и покажу не так уж много новых методов. Для решения большинства примеров достаточно будет знаний линейной алгебры, которые вы приобрели в главе 7. Приступим!

8.1. ВЫЧИСЛЕНИЕ СРЕДНЕГО РАСХОДА ПО ОБЪЕМУ

Для начала предположим, что нам известен объем нефти в резервуаре в каждый момент времени, а узнать его можно с помощью функции volume на Python.. Эта функция принимает время в часах, прошедшее с некоторого начального момента, и возвращает объем нефти в резервуаре в этот момент, измеряемый в единицах, называемых баррелями.. Чтобы сосредоточиться на сути, а не на алгебре, я даже не буду раскрывать формулу функции (те, кому это интересно, могут увидеть ее в примерах к книге).. Прямо сейчас вам нужно лишь несколько раз вызвать ее и построить график. Проделав это, вы должны получить график, изображенный на рис. 8.3.


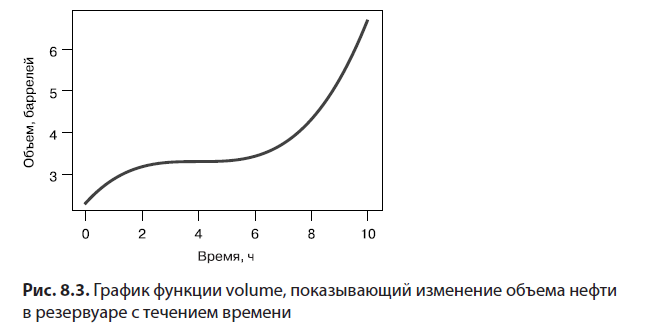
Наша текущая задача — определение скорости поступления нефти в резервуар в любой момент времени, поэтому начнем с того, что рассчитаем ее интуитивным способом. Для этого напишем функцию average_flow_rate(v, t1, t2), которая принимает функцию объема v, время начала t1 и время окончания t2 и возвращает число, представляющее среднюю скорость поступления нефти в резервуар за заданный интервал времени. То есть она должна сообщить нам среднюю скорость в баррелях в час, с какой нефть поступала в резервуар в течение этого времени.

8.1.1. Реализация функции average_flow_rate

Предлог «в» в единице измерения «баррели в час» предполагает выполнение деления для получения ответа. Чтобы найти средний расход (скорость поступления), нужно разделить значение изменения объема на прошедшее время:


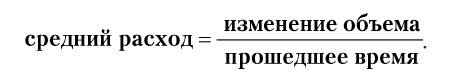
Прошедшее время — это интервал между временем начала t1 и окончания t2, измеренный в часах, который вычисляется как t2 – t1. Если есть функция V(t), которая сообщает объем как функцию от времени, то общее изменение объема равно разности объемов в моменты t2 и t1, или V(t2) – V(t1). Это дает нам более конкретное уравнение


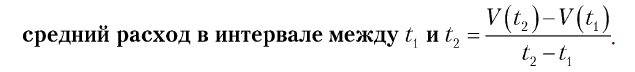
Именно так рассчитывается скорость изменений в различных контекстах. Например, скорость движения автомобиля — это расстояние, преодолеваемое за единицу времени. Чтобы вычислить среднюю скорость за поездку, нужно разделить пройденное в целом расстояние в милях на затраченное время в часах, получив скорость в милях в час. Чтобы узнать пройденное расстояние и затраченное время, нужно свериться с часами и одометром в начале и конце поездки.

Формула вычисления среднего расхода зависит от функции объема V и времени начала t1 и конца t2, которые можно передать соответствующей функции на Python с нужными параметрами. Тело функции — прямой перевод этой математической формулы на Python:

def average_flow_rate(v,t1,t2):
    return (v(t2) – v(t1))/(t2 – t1)

Это простая функция, но она важна, поэтому нужно уделить ей внимание.. Воспользуемся функцией volume (график которой изображен на рис. 8.3, а исходный код включен в набор примеров) и попробуем узнать среднюю скорость поступления нефти в резервуар между 4- и 9-часовой отметками. В этом случае t1 = 4, t2 = 9.. Чтобы найти начальный и конечный объемы, вызовем функцию volume с этими параметрами:

>>> volume(4)
3.3
>>> volume(9)
5.253125

Округлив для простоты полученные значения, находим разницу между двумя объемами, 5,25 – 3,3 = 1,95 барреля, а общее истекшее время составляет 9 – 4 = 5 часов. Таким образом, средний расход составляет примерно 1,95 барреля, деленные на 5 часов, или 0,39 барреля в час. Функция подтверждает, что мы все сделали правильно:

>>> average_flow_rate(volume,4,9)
0.390625

На этом завершаем первый простой пример определения скорости изменения функции. Это было не так уж сложно! Но прежде чем перейти к более интересным примерам, потратим еще немного времени на интерпретацию того, что делает функция вычисления объема.

8.1.2. Изображение среднего расхода секущей прямой

Еще один полезный способ оценить среднюю скорость изменения объема с течением времени — посмотреть на график объема. Сосредоточимся на двух точках на графике, между которыми мы рассчитали средний расход. На рис. 8.4 я соединил их прямой. Прямая, проходящая через две точки на таком графике, называется секущей.


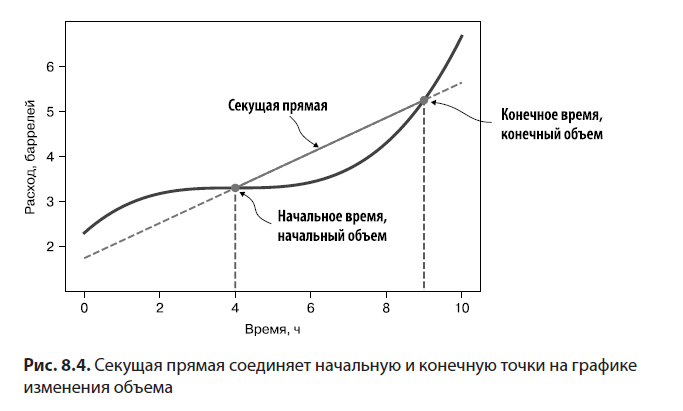
Как видите, отметка на графике, соответствующая 9 часам, находится выше отметки, соответствующей 4 часам, потому что за этот период объем нефти в резервуаре увеличился. В результате секущая прямая, соединяющая начальную и конечную точки, направлена вверх. Наклон секущей напрямую связан со средней величиной расхода на временном интервале, и вот почему. Наклон прямой, соединяющей две точки, пропорционален величине изменения вертикальной координаты, деленной на величину изменения горизонтальной координаты. При этом вертикальная координата изменяется от V(t1) до V(t2) на величину V(t2) – V(t1), а горизонтальная координата изменяется от t1 до t2 на величину t2 – t1. Затем V(t2) – V(t1) делится на t2 – t1, в точности как вычисляется средний расход (рис. 8.5)!


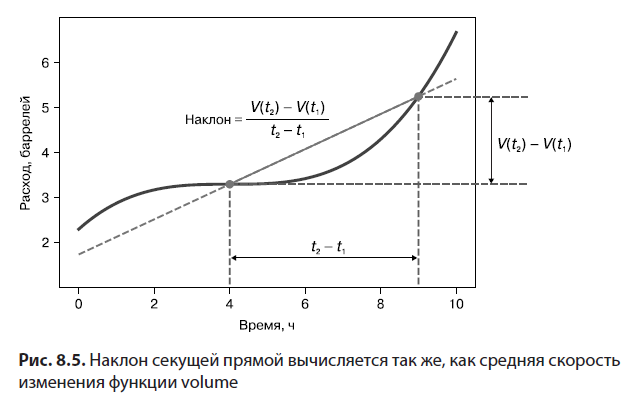
Рассуждая о средней скорости изменения функции, вы можете сами рисовать секущие прямые на графике.

8.1.3. Отрицательные скорости изменения

Следует упомянуть еще один случай, когда секущая прямая имеет отрицательный наклон. На рис. 8.6 показан график другой функции объема, которую можно найти в примерах к этой книге под именем decreasing_volume. На рис. 8.6 показан график уменьшения объема нефти в резервуаре с течением времени.

Этот пример противоречит предыдущему примеру, потому что мы не ожидаем, что нефть будет вытекать из резервуара обратно в землю. И все же он показывает, что секущая может быть направлена вниз, например, на интервале от t = 0 до t = 4.. В этом временном промежутке изменение объема нефти составило –3,2 барреля (рис. 8.7).



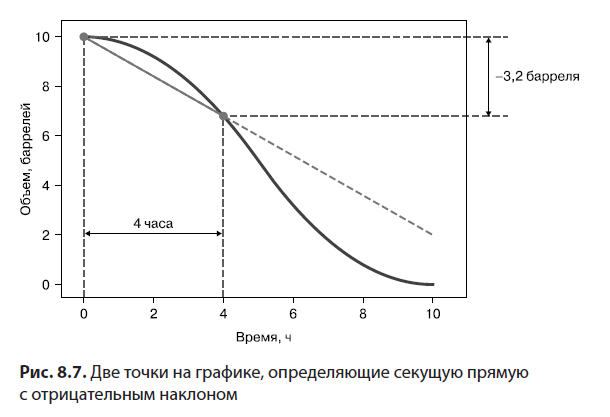
В этом случае наклон составляет –3,2 барреля, деленные на 4 часа, или –0,8 барреля в час. Это означает, что скорость поступления нефти в резервуар составляет –0,8 барреля в час. Правильнее было бы сказать, что нефть вытекает из резервуара со скоростью 0,8 барреля в час. Независимо от того, увеличивается или уменьшается функция объема, функция average_flow_rate надежно вычисляет скорость ее изменения. В данном случае

>>> average_flow_rate(decreasing_volume,0,4)
-0.8

Получив функцию вычисления скорости изменения объема, мы готовы сделать еще один шаг в следующем разделе и выяснить, как скорость изменяется во времени.

8.1.4. Упражнения

Упражнение 8.1. Представьте, что вы отправились в поездку в полдень, когда одометр показывал общий пробег 77 641 милю, и закончили ее в 16:30, когда одометр показывал 77 905 миль. Вычислите среднюю скорость за все время поездки.
Решение. Поездка продлилась 4,5 часа, пройденное расстояние составило 77 905 – 77 641 = 264 мили. Отсюда средняя скорость равна 264 мили/4,5 часа, или примерно 58,7 миль/ч.

Упражнение 8.2. Напишите функцию secant_line(f, x1, x2), которая принимает функцию f(x) и два значения, x1 и x2, и возвращает новую функцию, представляющую секущую прямую во времени. Например, после выполнения инструкции line = secant_line(f,x1,x2) вызов line(3) должен вернуть значение y секущей прямой, соответствующее x = 3.
Решение

def secant_line(f,x1,x2):
    def line(x):
        return f(x1) + (x-x1) * (f(x2)-f(x1))/(x2-x1)
    return line

Упражнение 8.3. Напишите функцию, которая использует код из предыдущего упражнения и рисует секущую прямую для функции f, соединяющую две заданные точки.
Решение

def plot_secant(f,x1,x2,color='k'):
    line = secant_line(f,x1,x2)
    plot_function(line,x1,x2,c=color)
    plt.scatter([x1,x2],[f(x1),f(x2)],c=color)

8.2. ГРАФИК ЗАВИСИМОСТИ СРЕДНЕЙ СКОРОСТИ ОТ ВРЕМЕНИ

Одна из наших главных целей в этой главе — на основе функции объема восстановить функцию скорости поступления нефти. Чтобы выразить скорость поступления в виде функции от времени, нужно узнать, как быстро меняется объем нефти в резервуаре в разные моменты. Во-первых, как показано на рис. 8.8, скорость поступления меняется во времени — разные секущие на графике объема имеют разный наклон.


В этом разделе мы приблизимся к определению расхода как функции от времени путем вычисления среднего расхода на разных интервалах.. Для этого разобьем 10-часовой период на несколько меньших интервалов фиксированной продолжительности (например, 10 интервалов по 1 часу) и вычислим средний расход для каждого.

Мы упакуем эти вычисления в функцию interval_flow_rates(v, t1, t2, dt), где v — функция объема, t1 и t2 — время начала и конца, а dt — фиксированная продолжительность временных интервалов. Эта функция будет возвращать список пар времени и расхода. Например, если мы разобьем 10 часов на сегменты по 1 часу, то результат должен выглядеть так:

[(0,...), (1,...), (2,...), (3,...), (4,...), (5,...), (6,...), (7,...),
 (8,...), (9,...)]

На месте многоточий… будут находиться значения расхода в соответствующие часы. Получив эти пары, мы сможем изобразить их в виде точечной диаграммы рядом с функцией расхода из начала главы и сравнить результаты.

8.2.1. Определение среднего расхода в разные промежутки времени

В качестве первого шага реализации interval_flow_rates() найдем начальные точки для каждого временного интервала. Это означает, что мы должны создать список значений времени от начального момента t1 до момента окончания t2 с шагом, равным длине интервала dt.

В библиотеке NumPy есть удобная функция arange, которая делает эту работу. Например, если передать ей интервал времени от 0 до 10 часов и задать продолжительность одного шага равной 0,5 часа, то она вернет следующий список значений, соответствующих началу каждого шага:

>>> import numpy as np
>>> np.arange(0,10,0.5)
array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. ,
       6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])

Обратите внимание на то, что отметка 10 часов, соответствующая времени окончания, не включена в список. Это связано с тем, что в список включаются отметки времени, соответствующие началу каждого получасового шага, а интервал от t = 10 до t = 10,5 не является частью общего временного интервала, который мы задали.

Прибавив продолжительность интервала dt к времени начала, можно получить время конца этого интервала. Например, интервал, начинающийся в 3,5 часа, заканчивается в 3,5 + 0,5 = 4 часа. Чтобы реализовать функцию interval_flow_rates, нужно просто вызвать функцию average_flow_rate для каждого интервала.. Вот как выглядит законченная функция:



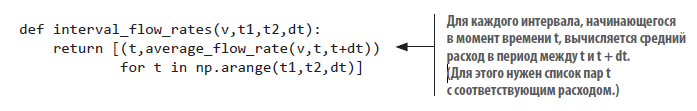
Если передать в вызов interval_flow_rates функцию volume, 0 и 10 часов в качестве времени начала и конца общего интервала и величину шага, равную 1 часу, то в ответ мы получим список, сообщающий скорость поступления нефти в каждый час:

>>> interval_flow_rates(volume,0,10,1)
[(0, 0.578125),
 (1, 0.296875),
 (2, 0.109375),
 (3, 0.015625),
 (4, 0.015625),
 (5, 0.109375),
 (6, 0.296875),
 (7, 0.578125),
 (8, 0.953125),
 (9, 1.421875)]

Глядя на этот список, можно подметить несколько аспектов. Средняя скорость поступления нефти всегда положительная, а это означает, что каждый час ее объем в резервуаре только увеличивался. Скорость поступления нефти снижается до минимального значения примерно через 3 и 4 часа, а затем увеличивается до максимального значения в последний час. Это станет еще очевиднее, если нанести скорость на график.

8.2.2. График интервальных расходов

Быстро построить график изменения расхода с течением времени можно с помощью функции scatter из библиотеки Matplotlib. Эта функция принимает два отдельных списка с горизонтальными и вертикальными координатами и рисует набор точек на графике. Чтобы воспользоваться ею, мы должны создать два списка с 10 значениями времени и расхода, а затем передать их функции. Чтобы не повторять процесс, объединим все в одну функцию:

def plot_interval_flow_rates(volume,t1,t2,dt):
    series = interval_flow_rates(volume,t1,t2,dt)
    times = [t for (t,_) in series]
    rates = [q for (_,q) in series]
    plt.scatter(times,rates)

Вызов plot_interval_flow_rates(volume,0,10,1) создаст точечную диаграмму на основе данных, полученных с помощью interval_flow_rates. На рис. 8.9 показан результат построения графика функции volume от нуля до 10 часов с шагом в 1 час.


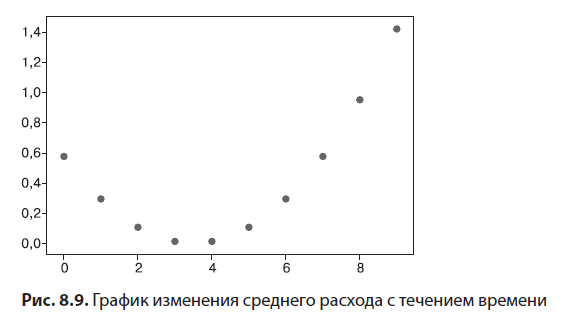
Этот график подтверждает наши умозаключения, сделанные на основе данных: средний расход уменьшается до самого малого значения на отметках 3 и 4 часа, а затем снова увеличивается до самого высокого значения, достигая почти 1,5 барреля в час. Сравним средние значения с фактической функцией расхода. Я не хочу грузить вас формулой зависимости расхода от времени, поэтому не буду приводить ее здесь. Но я включил функцию flow_rate в примеры с исходным кодом для этой книги, и мы можем построить ее график рядом с точечной диаграммой (рис. 8.10).


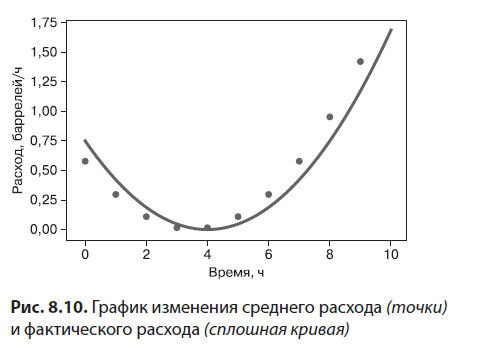
Эти два графика отражают один и тот же процесс, но не совсем точно совпадают.. Причина в том, что точечная диаграмма отражает средний расход, тогда как функция flow_rate показывает мгновенное значение расхода в любой момент времени.

Чтобы понять разницу, вспомним пример с поездкой на автомобиле. Если вы преодолели 60 миль за 1 час, то средняя скорость составит 60 миль/ч. Однако маловероятно, что в течение этого часа спидометр постоянно показывал ровно 60 миль/ч. В какой-то момент на прямых участках ваша мгновенная скорость могла достигать 70 миль/ч, а на извилистых или загруженных участках вы могли снизить ее до 50 миль/ч.

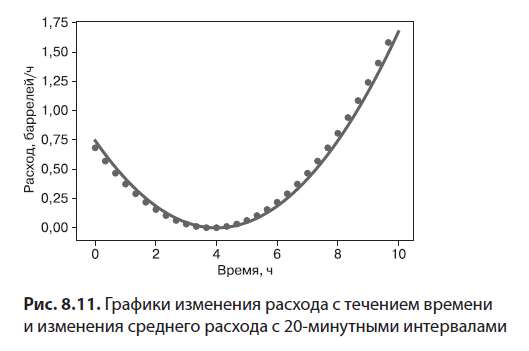
Точно так же показания расходомера на трубопроводе не обязательно должны согласовываться со средним расходом за текущий час. Получается, что если сделать временные интервалы меньше, то графики должны быть ближе друг к другу. На рис. 8.11 показаны графики функции мгновенного расхода и среднего расхода с 20-минутными интервалами (1/3 часа).

Средние значения расхода все еще неточно соответствуют мгновенному расходу, но теперь два графика намного ближе друг к другу. В следующем разделе мы воспользуемся этим приемом: вычислим средние значения расхода на очень маленьких интервалах и увидим, что при таких условиях разница между средним и мгновенным расходом практически незаметна.

8.2.3. Упражнения

Упражнение 8.4. Постройте график изменения расхода с течением времени, используя decreasing_volume и получасовые интервалы. Когда расход самый низкий? То есть когда нефть вытекает из бака с наибольшей скоростью?
Решение. Запустив plot_interval_flow_rates(decreasing_volume,0, 10,0.5), можно увидеть, что самый низкий расход (наибольшее по абсолютной величине отрицательное значение) — около отметки 5 часов.

Упражнение 8.5. Напишите функцию linear_volume_function и постройте график зависимости расхода от времени, чтобы показать, что расход не меняется.
Решение. Функция linear_volume_function(t) выполняет вычисления по формуле V(t) = at + b, где a и b — константы, например:

def linear_volume_function(t):
    return 5*t + 3

plot_interval_flow_rates(linear_volume_function,0,10,0.25)

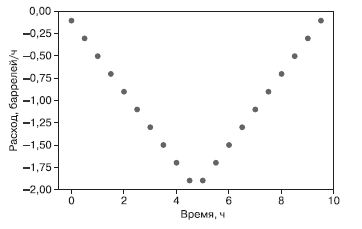
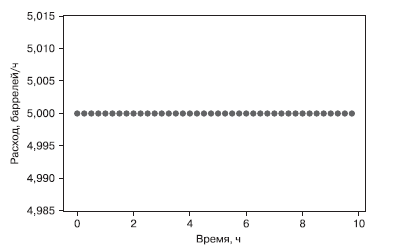
Этот график показывает, что для линейной функции изменения объема значение расхода постоянно во времени.

Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Python