Какой компьютер без демосцены? Обратимся к классике от @Manwe_SandS @frog:
До моего визита на Assembly'99 я каждый pаз удивлялся pезультатам голосования на заpубежных demo party. Мне было непонятно, как столько людей могут отдавать голоса за pаботы состоящие из тупой (я пpошу пpощения, но это именно так) последовательности эффектов - плазмы, туннеля, огня, вpащающегося куба (тоpа) и пpочих подобных вещей, не объединенных никаким сюжетом, не несущими никакой идеи.
То что нужно! Возьмём первый попавшийся релейный компьютер и понаделаем эффектов.
Движущаяся синусоида

Всякие движущиеся кривые встечаются в каждом втором демо. Часто их форма меняется, иногда по кривой бегают буквы. Множество красочных вариантов.
Но функцию синуса не так-то просто посчитать. На восьмибитных машинах быстро рисовать и перерисовывать синусоиду не получится - программе на Spectrum-Бейсике на одну кривую нужно секунд 15:
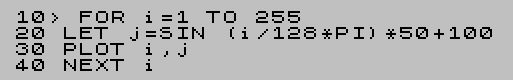
Даже если оптимизировать вывод на экран и расчёты, всё равно будет слишком медленно для демо. Но выход есть - это использование таблицы заранее посчитанных значений синуса.

Конечно вбивать их руками не нужно, можно заранее посчитать хоть и медленным алгоритмом, а потом экономить время, считывая готовые значения из таблицы. Выбор лишь в том, запускать этот расчёт на этапе разработки программы, вставляя готовую таблицу в исходный или бинарный файл, либо на этапе инициализации.
Для первого способа даже есть готовые генераторы, дающие примерно такой результат:
// Formula: sin(2*pi*t/T) const int16_t lut[1024] = { 0, 201, 402, 603, 804, 1005, 1206, 1407, 1608, 1809, 2009, 2210, 2410, 2611, 2811, 3012, 3212, 3412, 3612, 3811, 4011, 4210, 4410, 4609, 4808, 5007, 5205, 5404, ... }
Вторая часть, которая требует особенного подхода, это рисование синусоиды на экране. Ведь чтобы она двигалась, нужно постоянно обновлять картинку, а пикселей на экране много. Но положение всех точек каждый раз пересчитывать не требуется. Например, если мы хотим устроить скроллинг, то можно просто копировать цвета пикселей справа налево, а заново вычислять лишь самый правый столбец изображения. Скроллинг экрана настолько часто используется (например, в играх), что, к примеру, у Commodore C64 и NES для этого была аппаратная поддержка.
Вот и первый фрагмент нашего релейного демо:
Огонь
Огонь - это эффект, который сделать не очень сложно, а смотрится он красиво.

Алгоритм генерации похож на работу клеточного автомата: цвета каждого следующего "поколения" пикселей вычисляются на основе цветов предыдущего поколения. Начинает гореть огонь конечно снизу: последний ряд пикселей заполняется случайными значениями. Величина, которую хранит пиксель, может обозначать яркость или цвет - от чёрного через красный, оранжевый, жёлтый к белому.
Пламя обычно поднимается вверх, поэтому будем вычислять новые значения пикселей каждой строки, используя ту строку, что находится под ним.
Например, так появляющиеся внизу случайные точки будут подниматься вверх:
color[x][y] = color[x][y + 1]
Вот так они будут ещё и затухать:
color[x][y] = color[x][y + 1] ? color[x][y + 1] - 1 : 0
Вот так затухать на случайную величину:
int dec = rand() & 3; int c = color[x][y + 1]; c -= c >= dec ? dec : c; color[x][y] = c;
Ну и осталось использовать значения пикселей справа и слева, чтобы пламя не просто поднималось вверх, но и немного колебалось:
int dec = rand() & 3; int c = color[x][y + 1] * 3 + color[x - 1][y + 1] + color[x + 1][y + 1]; c /= 5; c -= c >= dec ? dec : c; color[x][y] = c;
Если теперь применить все эти знания, то получим вот такой результат:
Бегущая строка
Бегущая строка символов встречалась во многих демках. И не всегда это были ровные буквы, как в выпуске новостей по телевизору.

Иногда они двигались волнообразно

иногда по какой-то сложной трёхмерной поверхности

Встречались и несколько бегущих строк одновременно.
Традиционно в бегущей строке передавали приветы друзьям и знакомым. Но так как мы на хабре, то выведем традиционное "Hello, Habr!".
3D-лабиринт
Многие спрашивают, можно ли на релейном компьютере запустить Doom. Конечно можно! Даже на ZX-81 был 3D Monster Maze, а релейный компьютер поновее будет.

В демках трёхмерные лабиринты тоже встречались:

Для представления координат точек в трёхмерном пространстче обычно используются черырёхмерные вектора (x, y, z, 1). Тогда многие преобразования (поворот, сдвиг, ...) можно представить с помощью умножения этого вектора на матрицу:
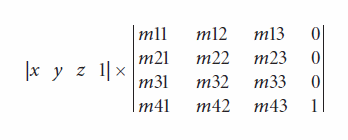
Современные процессоры даже включают в себя набор инструкций для ускорения таких расчётов.

Но так как такие инструкции были созданы, чтобы сводить программистов с ума, в релейном компьютере их нет. Только просты арифметические и логические команды, только хардкор. Кармак же написал Doom безо всяких MMX, значит и мы справимся:
Вот и всё, ребята
Вроде получилось отличное демо. Ещё и релюхами щёлкает, не то что Second Reality с этими вашими микросхемами.
