Эффективная сегментация изображений на графах

Сегментация изображений и выделение границ объектов (edge detection) играют важную роль в системах Computer Vision и применяются для задач распознавания сцен и выделения (определения) объектов. По большому счету, это такой же инструмент, как, например, сортировка, предназначенный для решения более высокоуровневых задач. И поэтому понимание устройства данного класса алгоритмов не будет лишним при построении подобных систем с учетом предъявляемых требований (в плане качество/производительность) и специфики поставленных задач.

В данной статье кратко описан алгоритм «Efficient Graph-Based Image Segmentation» авторов Pedro F. Felzenszwalb (MIT) и Daniel P. Huttenlocher (Cornell University), опубликованный в 2004 году. Да, алгоритм относительно старенький, но, несмотря на это, он до сих пор остается весьма популярным, демонстрируя неплохие результаты в плане производительности.

Под катом – большая смесь картинок и текста, не требовательная к текущему уровню знаний тематики. Любопытство приветствуется.



Сначала будет описан алгоритм на графах, на первый взгляд, имеющий мало общего с обработкой изображений. Однако чуть позже будет дана его интерпретация применительно к сегментации изображений.

Алгоритм Краскала

Алгоритм Краскала (wiki) строит каркас — минимальное остовное дерево данного графа. Далее будет использоваться английская аббревиатура MST (minimum spanning tree).

Задача: на карте расположено несколько населенных пунктов (на плате расположено несколько контактов), необходимо соединить все из них друг с другом таким образом, чтобы суммарная длина дорог (проводов) была минимальной.


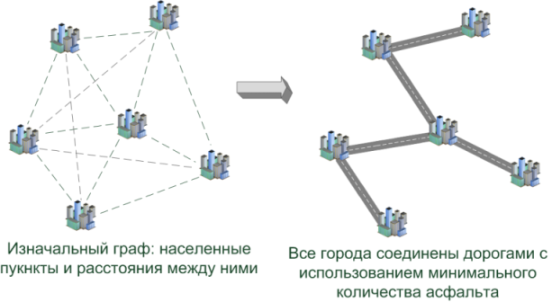
* Да, задача в такой формулировке обычно называется «задачей Штейнера» (статья), решив которую, города можно соединить еще дешевле. Но нам-то, в конечном итоге, не асфальт укладывать… =)

Для решения понадобятся:

• Графы: Кратко о том, что это такое и как они представляются в коде уже было изложено на Хабре (статья)
• Алгоритм Краскала (wiki): основной «движок» для решения задачи в такой формулировке. Он очень хорошо описан в библии Кормена, Лейзерсона «Алгоритмы: построение и анализ» (книга)
• Disjoint-set data structure (wiki): дополнительная структура, необходимая для эффективного выполнения вышеупомянутого алгоритма. Как она устроена, описано в той же библии, но только немного под другим названием (если не изменяет память: Union Find-Set, как-то так)

В текущей постановке задачи вершины графа (v_i) – представляют собой города, а ребра e(v_i, v_j) – дороги между городами. Нам известны расстояния между парами городов (v_i, v_j) – это вес ребер w(e(vi, vj)). Нужно найти MST, т.е. такое дерево в графе (без циклов: зачем строить лишние дороги), чтобы сумма ребер была минимальной и при этом все вершины были достижимы.

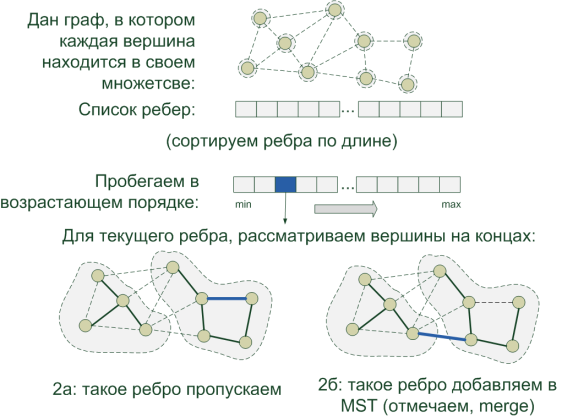
Изначально каждая вершина (город) сам по себе и является единственным гордым представителем соответствующего множества G₁, G₂, … G_N (по количеству вершин). Пусть пока думает, что именно она образовала MST. В ходе алгоритма мы эффективно и дипломатично объединим все эти разрозненные множества в одно единственное G так, чтобы участвующие в нем вершины образовали MST. Для этого:

• Сортируем все имеющиеся в графе ребра в порядке возрастания длины (дороги)
• Пробегая по ребрам в порядке возрастания длин, смотрим на концы ребра e = (a,b):
  • Если вершины (a и b) принадлежат одному множеству:Значит, они уже участвуют в некотором образованном подмножестве микро-MST, внутри их подграфа сумма ребер уже минимальна. Такое ребро пропускается – оно нам не нужно т.к. иначе оно образует цикл в дереве, и мы зря израсходуем асфальт
  • Если вершины (a и b) принадлежат разным подмножествам микро-MST:Нужно объединять, т.к. мы нашли ребро (дорогу) минимальной длины, объединяющее (сливающее) оба подмножества в одно. Все ребра меньшей длины уже рассмотрены и дешевле, чем этим ребром, объединить не получится. Такое ребро заносится в список ребер, использованных при построении дерева MST, а множества объединяются в одно
  • Продолжаем цикл объединения до получения одного единственного множества, равного искомому MST, в котором будут присутствовать все вершины графа
• Получаем одно единственное множество вершин (MST) и список ребер, использованных для его объединения, который представляет собой дерево минимальной суммарной длинны, объединяющее все вершины.

Disjoint-set data structure

Для реализации понятия «множество» в алгоритме Краскала применяется структура данных Disjoint-set data structure. Работа с ней оптимизирована на выполнение двух основных операций:

• Узнать для некоторой вершины, какому множеству в текущий момент она принадлежит
• Быстро объединить эти множества в одно

Чтобы приблизиться к теме сегментации изображений, описание продолжим в терминологии пикселей изображения и их цвета. Допустим, мы сегментируем попугайчика на фоне какого-нибудь Японского синего моря. Сначала каждый пиксель (вершина графа) будет сам по себе – в собственном сегменте (множестве), но в ходе алгоритма пиксели (вершины) «схожего» цвета (одного объекта) постепенно объединяются в один сегмент.

Допустим, на определенном шаге алгоритма попалось ребро, соединяющее два соседних пикселя: на одном конце ребра пиксель «оранжевый», а на другом «красный». Длину ребра определим как «разницу цвета» между пикселями. Все ребра меньшей длины (со схожим цветом) уже объединены: наверняка уже выделен оранжевый и красный сегмент попугайчика. Следуя алгоритму, нам нужно узнать, в одном ли сегменте лежат текущие «оранжевый» и «красный» пиксель? Если в разных, и мы считаем, что сегменты по цвету схожи, то объединяем их в один и продолжаем построение… В общем, тот же алгоритм Краскала, только с пикселями.

Используемая для этих операций структура – очень похожа на дерево (хотя и реализуется массивом индексов). В ней для каждого пикселя указан предок, т.е. указатель (индекс) на некоторый схожий по цвету пиксель, находящийся в том же самом сегменте. Основные операции:

• Поиск сегмента некоторого пикселя 'x': идем по предкам до самого верха. Самый верхний пиксель – это корень дерева, «представитель» данного сегмента на текущий момент.
• Объединение сегментов. Если у пикселей разные «представители» — значит, они принадлежат различным сегментам, иначе корень был бы один. Для их объединения «представителя» сегмента меньшей высоты (от самого далекого пикселя до корня) ссылаем (из него указываем) на более длинного «представителя», чтобы не увеличивать высоту дерева. Теперь имеем объединенный сегмент с общим представителем.
• Для того, чтобы в следующий раз не бегать далеко от пикселя к корню, после того, как «представитель» будет успешно обнаружен, устанавливаем прямую ссылку из пикселя – сразу на него. Это сокращает путь следующих поисков, и называется "path compression".

Отлично, теперь мы можем эффективно искать сегменты по пикселям и объединять их, а так же выстраивать MST по алгоритму Краскала. Пора узнать, как принимается решение о соединении или разделении двух областей.

Разделяй и властвуй

Алгоритм сегментации должен четко определять, где заканчивается один сегмент и начинается другой. Как правило, границы представляют собой характерные перепады яркости и/или оттенков цвета, встречающиеся на участках объект-фон, плоскость-тень, попугайчик-море, надпись на заборе… И если «перепад» больше некоторого «порога» (threshold), то из этого должно следовать, что это разные сегменты. Но есть небольшая проблемка: перепады могут сильно варьироваться для различных объектов, и сегменты сложно «отделить» однозначно заданной (const) пороговой величиной (threshold). Для поверхности стола на фоне стены: перепады соседних пикселей вдоль поверхности стола (стены) будут относительно небольшими, а вот на границе стол-стена будет скачок, который и разделит сегменты. Это ясно. А если у нас попугайчик на фоне моря? Он же сам очень «пестрый», внутри него большие перепады интенсивности (зеленый-красный-желтый-…), чтобы его «отделить» от моря, нужен другой «порог» (threshold). И постепенно приходим к выводу, что порог, который решает, что соседним сегментам «не суждено быть вместе», должен опираться не только на локальные показатели: перепад интенсивностей вдоль одного ребра (соединяющего соседние пиксели), но и на то, насколько эти сегменты сами по себе гладкие (в плане цвета) или «пестрые».

Серые картинки

Прежде чем перейти к обработке полноценных цветных картинок, рассмотрим упрощенный вариант, когда изображение представлено градациями серого (grayscale), т.е. в каждой ячейке матрицы изображения хранится число в интервале [0...1], представляющее собой яркость пикселя.

Efficient Graph-Based Image Segmentation

Каждый пиксель изображения представляется вершиной в графе. А вес (длина) ребра, соединяющего соседние вершины, выражается формулой: w(v_i,v_j)=|I(p_i)-I(p_j)|, где I(p_i) – интенсивность (яркость) пикселя p_i

В ходе выполнения алгоритма Краскала, на промежуточном этапе мы будем иметь несколько разрозненных сегментов (подмножеств пикселей), с минимальным суммарным весом ребер внутри: сегменты будут объединены ребрами минимальной длины, т.е. с минимальными «перепадами интенсивностей» между соседними пикселями. Поэтому соседние пиксели внутри одного сегмента будут схожи по цвету. Но только до некоторого значения максимального ребра (перепада интенсивности)…

И вот… мы взяли минимальное на текущем шаге ребро. Для двух пикселей, являющихся смежными вершинами этого ребра, определяем из одного ли они (уже построенного) сегмента?

• Да, из одного сегмента: просто продолжаем выполнение алгоритма.
• Нет. Необходимо определить, представляют ли сегменты части одного и того же объекта на изображении и их следует объединить, или их интенсивности «существенно» различаются?

Для определения различия между сегментами, с каждым уже построенным сегментом мы ассоциируем некоторую величину – максимальный перепад интенсивностей внутри него, т.е. самое длинное ребро в MST внутри сегмента:

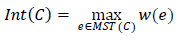
Отдельно его искать не придется – достаточно просто сохранять длину ребра, добавляемого при объединении составляющих «подсегментов». Ведь на момент объединения длина добавляемого ребра была больше, чем в уже построенных MST каждого «подсегмента», т.к. ребра обрабатываются в возрастающем порядке.

Получаем примерное решающее правило для сегментов C₁, C₂:

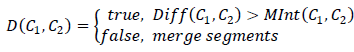
	Признак: следует ли разграничить эти сегменты
	Текущее ребро минимальной длины, соединяющее два разрозненных сегмента
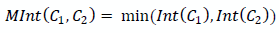	Меньший (из больших) перепад интенсивностей внутри одного из рассматриваемых сегментов

Получается что, для того чтобы сегменты «объединились», перепад интенсивностей на их границе должен быть меньше максимального перепада внутри каждого из объединяемых сегментов:

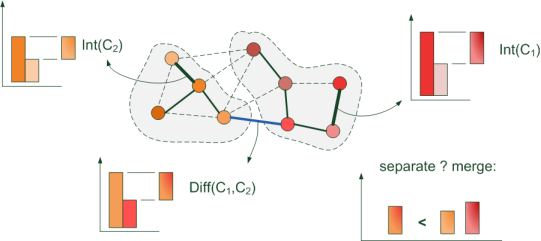
Ищу тебя

Как же построить граф по изображению? Какие пиксели являются соседними? На поверхности лежат два основных подхода:

• 4-connected: каждый пиксель соединяем с соседними сверху / снизу / слева / справа. Такое построение привлекательно тем, что количество ребер в графе минимально.
• 8-connected: дополнительно к предыдущему варианту каждый пиксель соединяем с соседними, находящимися по диагонали. Ребер, таким образом, в графе получается больше, алгоритм выполняется несколько медленнее. Но получаемая сегментация должна быть качественней – ведь учитывается больше связей между пикселями.

Алгоритм должен давать более качественные результаты на 8-connected построенном графе, однако 4-connected дает весьма приемлемые результаты и при этом выполняется значительно быстрее. А в качестве «расстояния» для обработки цветных изображений можем взять вот такую простую разницу цвета пикселей, как реализовано у авторов алгоритма:

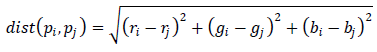
Однако, у такой формулировки расстояния есть недостаток. Если рассматривать «перепад интенсивности» между локально соседними пикселями, то небо на следующей картинке будет разбито на 2 отдельных сегмента проходящей поперек проволокой, или получим еще худший результат, если обработаем лужайку на фоне сетки:


Каждый фрагмент лужайки – будет отмечен как отдельный сегмент, но ведь это один объект!

Поэтому в альтернативном варианте, авторы предлагают рассматривать не только близлежащие пиксели, а оттолкнувшись от локальных свойств изображения (пикселей, располагающихся в непосредственной близости), попробовать «перепрыгнуть через провод» (см. картинку) и дотянуться до продолжения сегмента, находящегося на некотором удалении. Для этого в качестве длины ребра они предлагают выбрать Евклидово расстояние, зависящее как от положения пикселей (x,y), так и от их цвета (r,g,b):

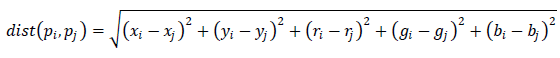
Теперь пиксели будут считаться «соседями», если они расположены рядом, либо имеют схожий оттенок, хотя физически могут находиться на некотором удалении. Для построении графа авторы предлагают каждый пиксель соединять с 10 (20, 30) «ближайшими». Это дает более качественную сегментацию, но требует больше вычислительных ресурсов.

Stick together, team!

Возвращаясь в самое начало. Давным-давно, когда все пиксели были разрознены – между соседними мог наблюдаться существенный перепад интенсивностей, не позволяющий им объединяться (merge). Вряд ли нам предоставили микроскопическую фотографию, где каждый пиксель надо обособить — скорее всего, они являются частью какого-то большего объекта (попугайчика). Чтобы они поддавались «слиянию» (merge) в большей степени, чем уже построенные большие сегменты, для которых более важна корректность разбиения, в решающем правиле добавляют величину, зависящую от размера построенного сегмента: 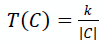, где |C| – мощность рассматриваемого сегмента (количество пикселей в нем на текущий момент), а k – это уже параметр сегментации, задаваемый вручную. С подобной поправкой в решающем правиле будет использоваться формула:


«Поправка» постепенно нивелируется с ростом сегмента (увеличением |C|)…

На самом деле, вместо подобного задания T можно выбрать и иную функцию, учитывающую специфику обрабатываемых изображений: форму сегментов, положение на фотографии, определенные цветовые оттенки…

Размытие по Гауссу

Возвращаясь к очень «пестрым» картинкам:


Ясно, что при определении расстояния между пикселями в таком определении, как «перепад интенсивностей», пиксели «пестрого», пусть даже единого объекта, будут не очень-то податливы на объединение в один объект. Чтобы сделать их более «сговорчивыми» на объединение и убрать шум/артефакты, к изображению обычно применяется размывание (smoothing) фильтром Гаусса (http://habrahabr.ru/blogs/webdev/43895/) с некоторым радиусом (среднеквадратическим отклонением) sigma. Это вызывает «взаимопроникновение» цветовых составляющих пикселей, и они более охотно идут на контакт.

Итого

Методов для сегментации существует много: различные подходы очень хорошо описаны в статье — «Методы сегментации изображений: автоматическая сегментация». А по большому счету, сегментация должна быть либо качественной, либо производительной, а если повезет – то все и сразу. Описанный выше метод представляет собой именно производительный вариант.

В таком способе сегментации самым трудоемким процессом является сортировка всех ребер, выполняемая за O(elog⁡e), где e – это количество ребер в графе. Таким образом, для изображения NxM пикселей ребер будет: |e| = 4*N*M

Исходный код алгоритма доступен по этой ссылке.

А как же OpenCV?

Во всеми любимой библиотеке OpenCV (wiki) есть метод "cvPyrSegmentation", т.е. пирамидальный метод сегментации изображений. Он устроен несколько иначе. Его описание заняло бы еще одну статью, поэтому — картинка. Сегменты строятся слоями (level), объединяя схожие по цвету пиксели в один (находящийся слоем выше), и далее последовательно обрабатывая слои находящиеся на следующем уровне (level) выше «до упора»:


В 2006 в Univesity of Malaga (Spain) было проведено сравнение нескольких пирамидальных алгоритмов и результаты изложены в следующей статье:


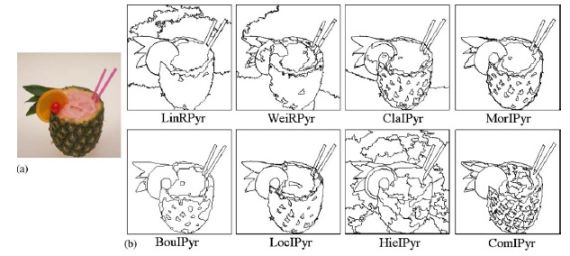
Авторы пришли к выводу, что из 8 методов, заслуживающими внимания являются 3, благодаря которым получаются достаточно качественные результаты разбиения изображения на объекты. Однако стоит отметить, что время выполнения пирамидальных алгоритмов колеблется от 0,5 сек. до 4,5 сек. (256x256 пикселей на Pentium 766 MHz), тогда как рассматриваемый "Efficient Graph-Based Image Segmentation" выполняется со слов авторов «in fraction of a second». У нас 1024x768 фотография отрабатывала за 0,5 сек (U9400 2 x 1.4GHz) внутри «матрешки»: VMWare – Matlab – mex (C++). В общем, пирамидальные – качество, описанные в статье графы – скорость. Оба имеют право на жизнь. =)


Самым усидчивым читателям, раскроем тайну «волшебных пузырьков»: что за цифры изображены на картинках? Это просто параметры метода "segmentation(sigma, k, min)", с 2-мя из которых вы уже знакомы, а 3-ий "min" — это принудительно установленный минимальный размер сегмента, чтобы «маленьких» не оставалось.


Удачи!

P.S. Прошу сильно не пинать, это мой девятый пост на Хабре.